Leetcode 3077. Maximum Strength of K Disjoint Subarrays
- Leetcode 3077. Maximum Strength of K Disjoint Subarrays
- 1. 解题思路
- 1. 朴素思路
- 2. 算法优化
- 2. 代码实现
- 1. 解题思路
- 题目链接:3077. Maximum Strength of K Disjoint Subarrays
1. 解题思路
这道题很惭愧没有搞定,思路上出现了差错,导致一直没能搞定,最后是看了大佬的算法才搞定的,唉,不过确实比较巧妙,因此这里把我们的朴素实现思路和大佬们的思路都在这里整理一下,留个记录。
1. 朴素思路
首先,我拿到这道题目之后的一个朴素的思路就是动态规划,显然,我们就是要将一个长度为n的arr分成k段,然后在每段当中获取最大/最小的subarray的和,然后乘以因子之后求和获取最大值。
因此,我们用一个动态规划即可处理这个问题。
然后,对于中间的每一个subarry,对于如何其中最大最小值的问题,我们用一个累积数组就可以将问题转换为如何求一个array的任意元素之后最大/最小元素的问题,这个是简单的。
因此,我们就可以快速给出代码如下:
class Solution:def maximumStrength(self, nums: List[int], k: int) -> int:n = len(nums)s = list(accumulate(nums, initial=0))factors = [(i+1)*(-1)**(i%2) for i in range(k)]print(s)@lru_cache(None)def dp(idx, r):if r == 0:return 0ans = -math.infif r % 2 == 1:_min = s[idx]sub = -math.inffor i in range(idx+1, n-r+2):sub = max(sub, s[i] - _min)_min = min(_min, s[i])ans = max(ans, factors[r-1] * sub + dp(i, r-1))else:_max = s[idx]sub = math.inffor i in range(idx+1, n-r+2):sub = min(sub, s[i] - _max)_max = max(_max, s[i])ans = max(ans, factors[r-1] * sub + dp(i, r-1))return ansans = dp(0, k)return ans
不过这段代码遇到了超时问题,无法正常通过。
其原因在于虽然动态规划的总的时间复杂度是 O ( N K ) O(NK) O(NK),但是由于内部还有一重循环,导致最坏的情况下时间复杂度变成了 O ( N 2 K ) O(N^2K) O(N2K),这显然就无法通过测试样例了。
2. 算法优化
而大佬的思路则是和我们相反的,我们是考虑如何将整体的array进行分段,大佬的思路则是考察array当中每一个元素的归属,显然,这只有以下几种情况:
- 哪个subarray都不属于
- 属于某一个subarray
- 与前一个元素都属于同一个subarray
- 是一个新的subarray第一个元素
此时,我们只需要给出两个 k k k维的动态规划向量dp0, dp1,对于某一个元素,他们的任意一维i分别表示:
dp0[i]表示当前元素属于第 i i i个subarray时,能够获得的最大strengthdp1[i]表示之前所有元素被分为 i i i个subarray时,能够获得的最大strength
此时,我们显然有迭代关系:
d p 0 t ( i ) = α ⋅ n i + m a x ( d p 0 t − 1 ( i ) , d p 1 t ( i − 1 ) ) d p 1 t ( i ) = m a x ( d p 1 t − 1 ( i ) , d p 0 t ( i ) ) \begin{aligned} dp0_{t}(i) &= \alpha \cdot n_i + \mathop{max}(dp0_{t-1}(i), dp1_{t}(i-1)) \\ dp1_{t}(i) &= \mathop{max}(dp1_{t-1}(i), dp0_{t}(i)) \end{aligned} dp0t(i)dp1t(i)=α⋅ni+max(dp0t−1(i),dp1t(i−1))=max(dp1t−1(i),dp0t(i))
由此,遍历整个长度为n的array,我们即可从dp1中得到其所有元素被分至 k k k个subarray时能够获得的最大strength。
我们将其翻译为代码语言即可。
2. 代码实现
给出python代码实现如下:
class Solution:def maximumStrength(self, nums: List[int], k: int) -> int:factors = [(k-i)*(-1)**(i%2) for i in range(k)]# dp0 stand for consecutive and dp1 for inconsecutivedp0 = [-math.inf for _ in range(k)]dp1 = [-math.inf for _ in range(k)]for num in nums:# s[i] stand for max result including num in ith subarrays = [-math.inf for _ in range(k)]s[0] = num * factors[0] + max(0, dp0[0])for i in range(1, k):s[i] = num * factors[i] + max(dp0[i], dp1[i-1])for i in range(k):dp1[i] = max(dp1[i], s[i])dp0 = sreturn dp1[-1]
提交代码评测得到:耗时2386ms,占用内存18MB。
相关文章:

Leetcode 3077. Maximum Strength of K Disjoint Subarrays
Leetcode 3077. Maximum Strength of K Disjoint Subarrays 1. 解题思路 1. 朴素思路2. 算法优化 2. 代码实现 题目链接:3077. Maximum Strength of K Disjoint Subarrays 1. 解题思路 这道题很惭愧没有搞定,思路上出现了差错,导致一直没能…...

【JetsonNano】onnxruntime-gpu 环境编译和安装,支持 Python 和 C++ 开发
1. 设备 2. 环境 sudo apt-get install protobuf-compiler libprotoc-devexport PATH/usr/local/cuda/bin:${PATH} export CUDA_PATH/usr/local/cuda export cuDNN_PATH/usr/lib/aarch64-linux-gnu export CMAKE_ARGS"-DONNX_CUSTOM_PROTOC_EXECUTABLE/usr/bin/protoc&qu…...

知名比特币质押协议项目Babylon确认参加Hack.Summit()2024区块链开发者大会
Babylon项目已确认将派遣其项目代表出席2024年在香港数码港举办的Hack.Summit()2024区块链开发者大会。作为比特币生态的领军项目,Babylon积极参与全球区块链领域的交流与合作,此次出席大会将为其提供一个展示项目进展、交流技术与创新思路的重要平台。B…...
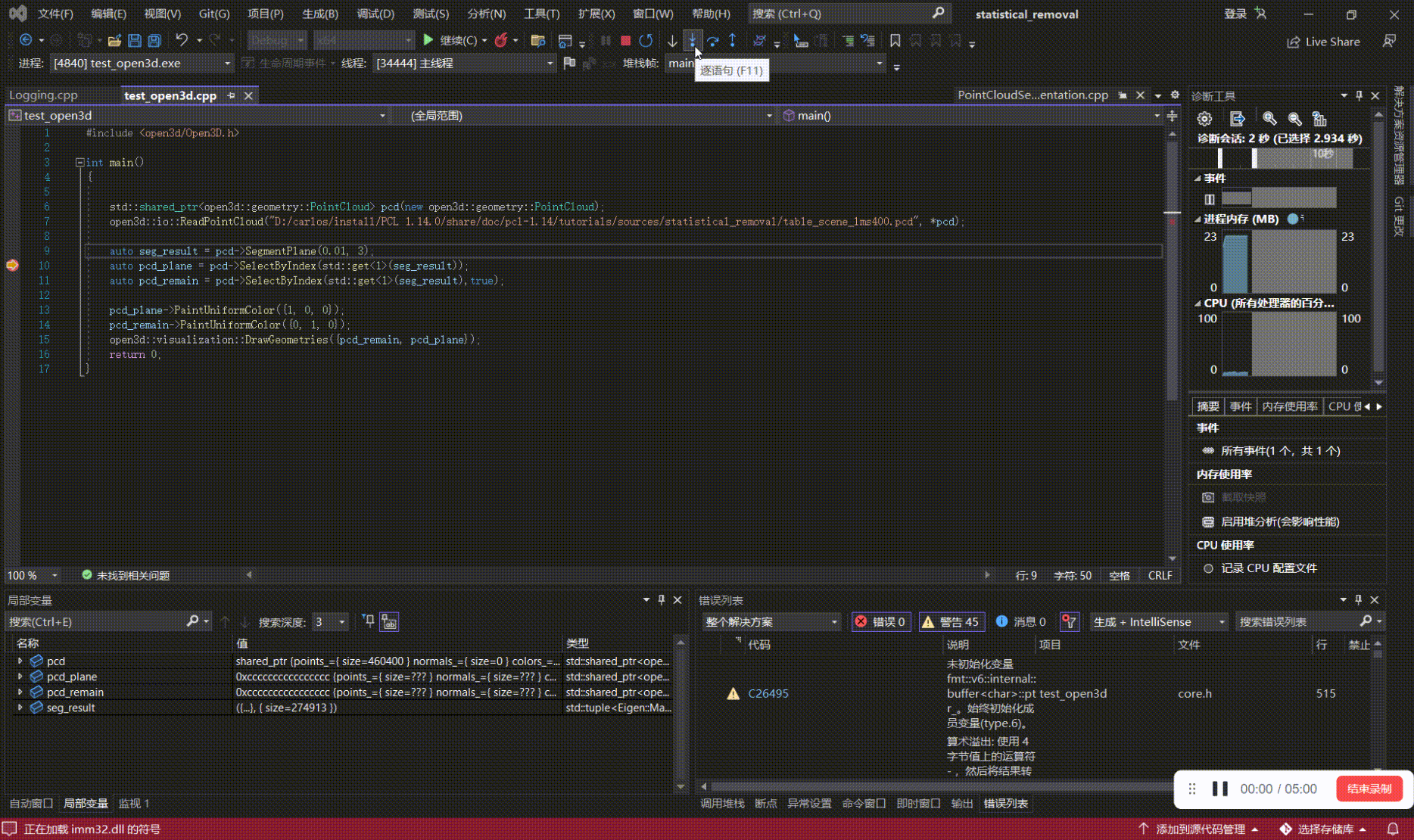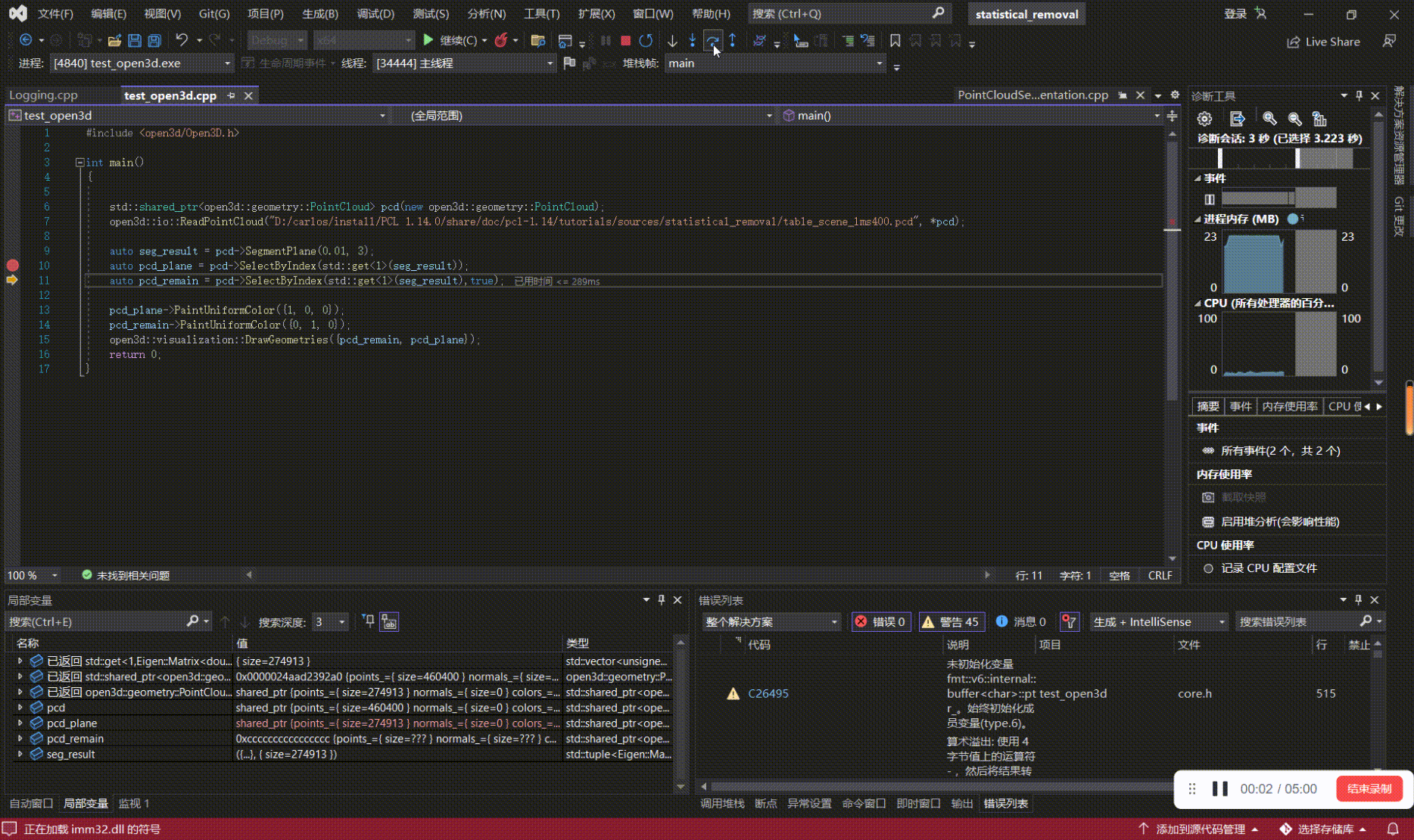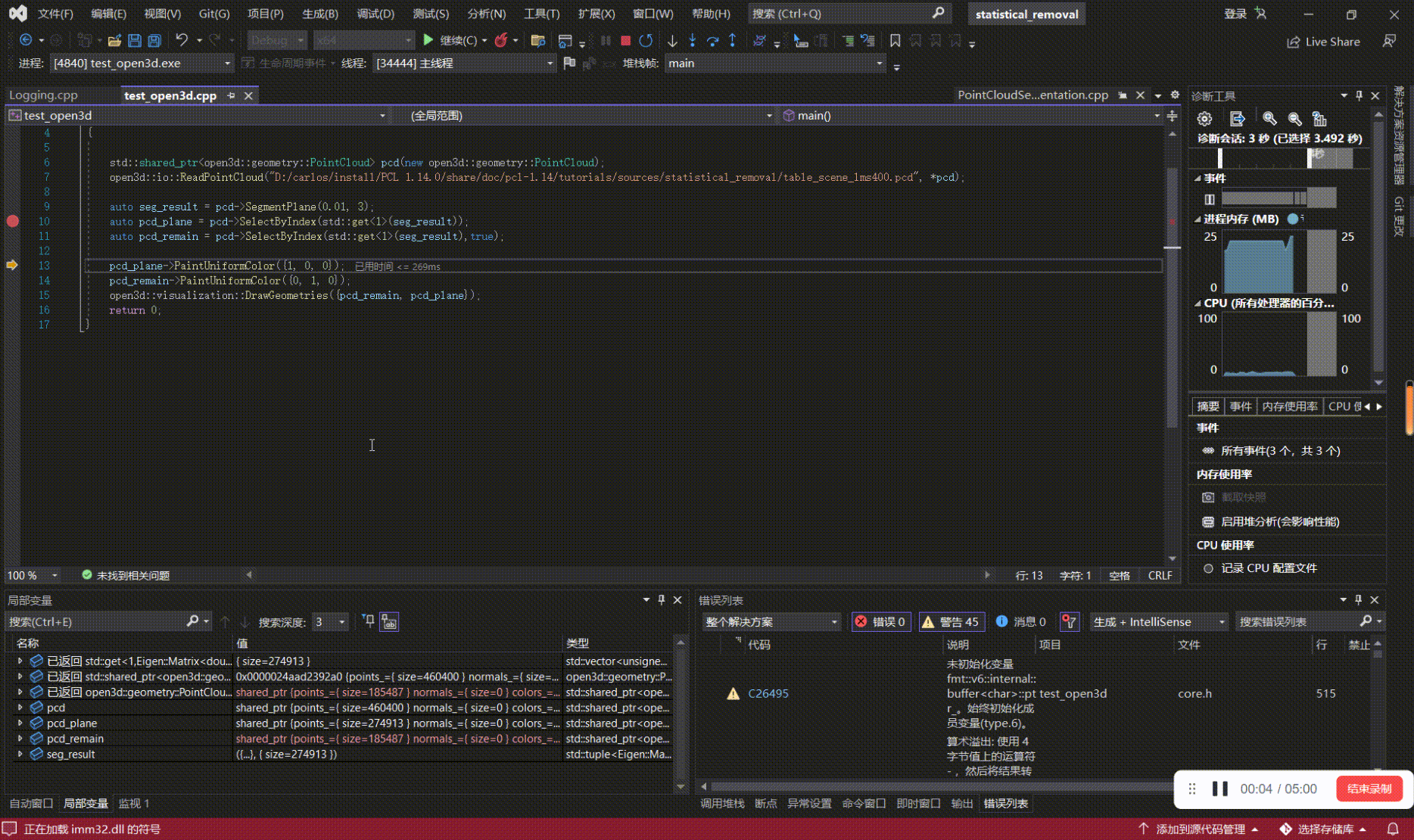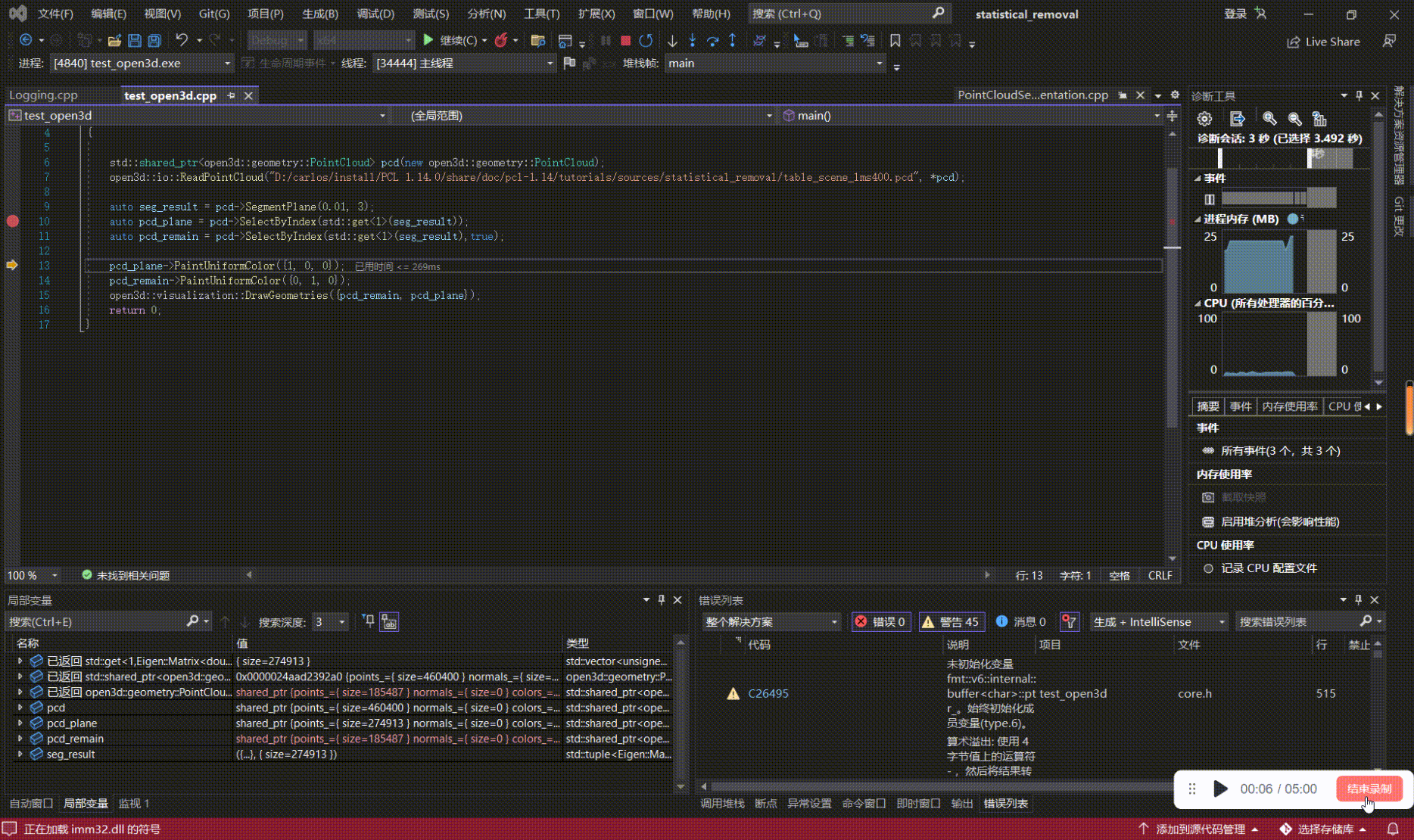
如何学习、上手点云算法(三):用VsCode、Visual Studio来debug基于PCL、Open3D的代码
写在前面 本文内容 以PCL 1.14.0,Open3D0.14.1为例,对基于PCL、Open3D开发的代码进行源码debug; 如何学习、上手点云算法系列: 如何学习、上手点云算法(一):点云基础 如何学习、上手点云算法(二):点云处理相…...

【干货】alzet渗透泵操作说明
alzet渗透泵是一款小型、可植入式的胶囊渗透泵产品,此产品由于其独特的渗透原理,深受广大科研人员的喜爱。该泵可适用于小鼠、大鼠及其他实验动物的研究,并且alzet渗透泵可减轻科研人员夜间及周末给药的困扰。alzet渗透泵无需外部连接或频繁处…...
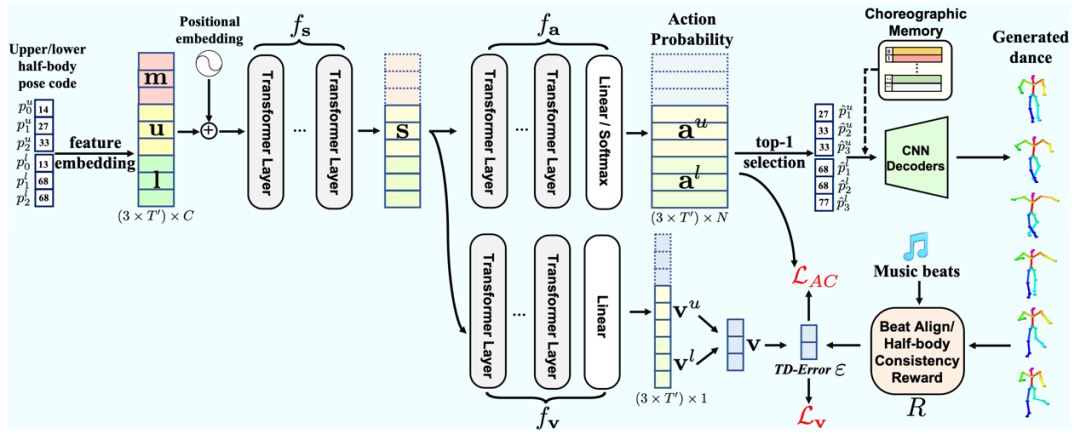
CVPR 2022 Oral | Bailando: 基于编舞记忆和Actor-Critic GPT的3D舞蹈生成
目录 测试结果: 02 提出的方法 测试结果: 预测有3个步骤,速度比较慢 02 提出的方法 1. 针对舞蹈序列的VQ-VAE和编舞记忆 与之前的方法不同,我们不学习从音频特征到 3D 关键点序列的连续域的直接映射。相反,我们先让…...

解读电影级视频生成模型 MovieFactory
Diffusion Models视频生成-博客汇总 前言:MovieFactory是第一个全自动电影生成模型,可以根据用户输入的文本信息自动扩写剧本,并生成电影级视频。其中针对预训练的图像生成模型与视频模型之间的gap提出了微调方法非常值得借鉴。这篇博客详细解读一下这篇论文《MovieFactory:…...
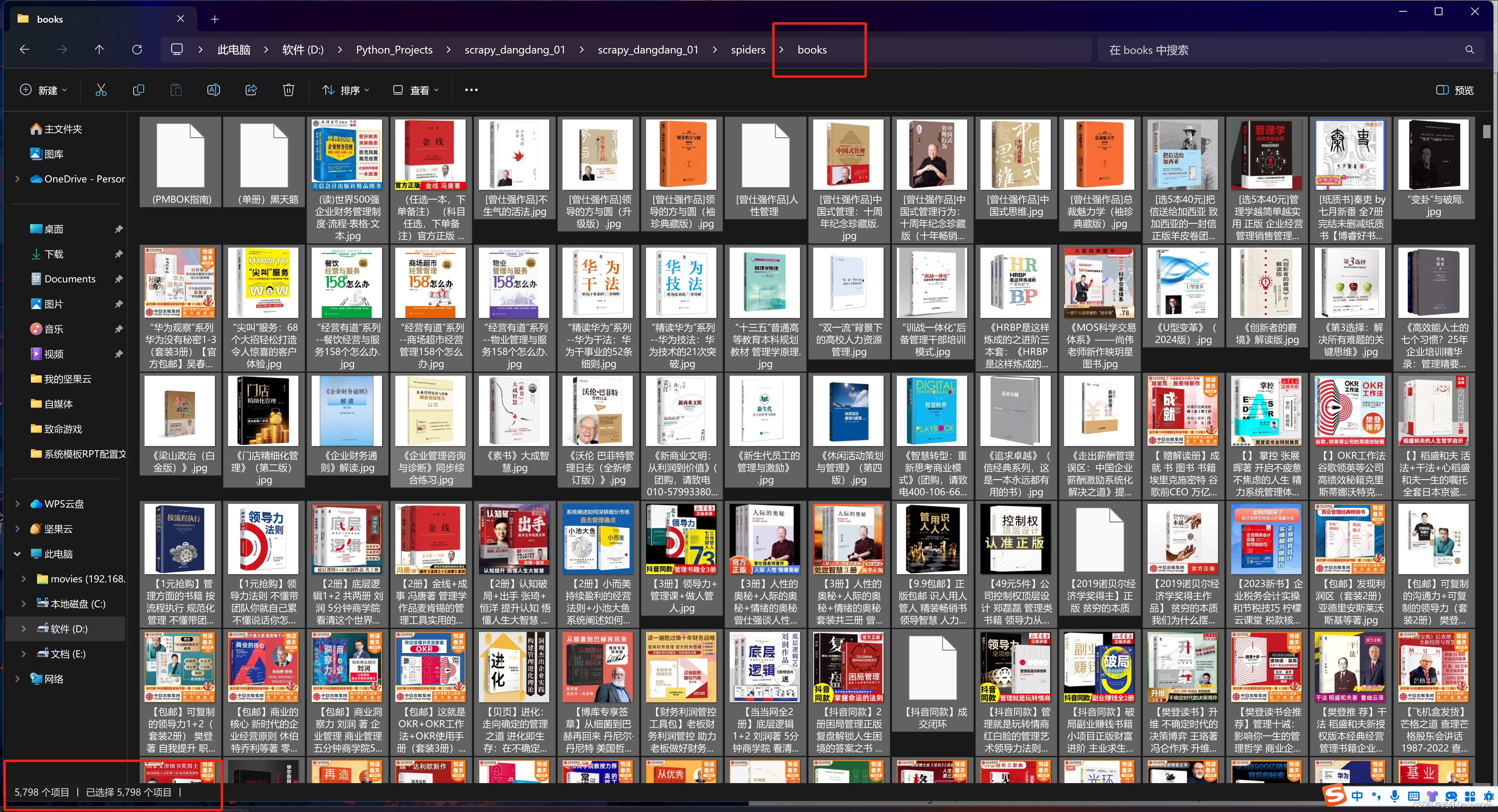
【Python从入门到进阶】50、当当网Scrapy项目实战(三)
接上篇《49、当当网Scrapy项目实战(二)》 上一篇我们讲解了的Spider与item之间的关系,以及如何使用item,以及使用pipelines管道进行数据下载的操作,本篇我们来讲解Scrapy的多页面下载如何实现。 一、多页面下载原理分…...

【调试记录】vscode远程连接问题汇总
1. kex_exchange_identification kex_exchange_identification: read: Connection reset by xxx.xx.xx.x 一直连不上实验室的服务器,用PUTTY和Mobaxterm也不行(报错:Remote side unexpectedly closed network connection)。已知…...

基于springboot的疾病防控综合系统
采用技术 基于springboot的疾病防控综合系统的设计与实现~ 开发语言:Java 数据库:MySQL 技术:SpringBootMyBatis 工具:IDEA/Ecilpse、Navicat、Maven 系统效果展示 用户功能效果 打卡管理 接种记录查看 公告信息查看 社区…...

js实现文本内容过长中间显示...两端正常展示
实现效果 实现思路 获取标题盒子的真实宽度, 我这里用的是clientWidth;获取文本内容所占的实际宽度;根据文字的大小计算出每个文字所占的宽度;判断文本内容的实际宽度是否超出了标题盒子的宽度;通过文字所占的宽度累加之和与标题…...

Buran勒索病毒通过Microsoft Excel Web查询文件进行传播
Buran勒索病毒首次出现在2019年5月,是一款新型的基于RaaS模式进行传播的新型勒索病毒,在一个著名的俄罗斯论坛中进行销售,与其他基于RaaS勒索病毒(如GandCrab)获得30%-40%的收入不同,Buran勒索病毒的作者仅占感染产生的25%的收入,…...
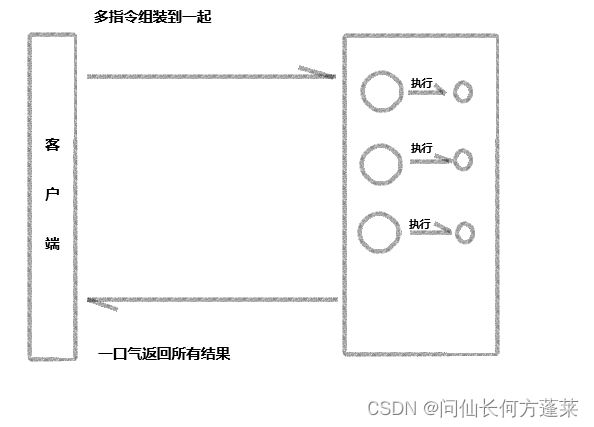
中间件 | Redis - [基本信息]
INDEX 1 常规用法2 QPS3 pipeline 1 常规用法 分布式锁 最常见用法,需要注意分布式锁的redis需要单点 分布式事务 分布式事务中,核心的技术难点其实是分布式事务这个事本身作为数据的持久化 2PC,比如 seata 的 AT 模式下,将 un…...

【Docker】Neo4j 容器化部署
Neo4j环境标准软件基于Bitnami neo4j 构建。当前版本为5.17.0 你可以通过轻云UC部署工具直接安装部署,也可以手动按如下文档操作,该项目已经全面开源,可以从如下环境获取 配置文件地址: https://gitee.com/qingplus/qingcloud-platform Qin…...

Visual studio编译器报1个无法解析的外部命令
解决思路:(以下思路需对照代码进行逐点分析) ①:代码里函数有声明,但是没有定义 (初学者错这个比较多) ②:类中有静态变量成员,没有对它进行初始化(是变量&…...

微信小程序(五十三)修改用户头像与昵称
注释很详细,直接上代码 上一篇 新增内容: 1.外界面个人资料基本模块 2.资料修改界面同步问题实现(细节挺多,考虑了后期转服务器端的方便之处) 源码: app.json {"window": {},"usingCompone…...
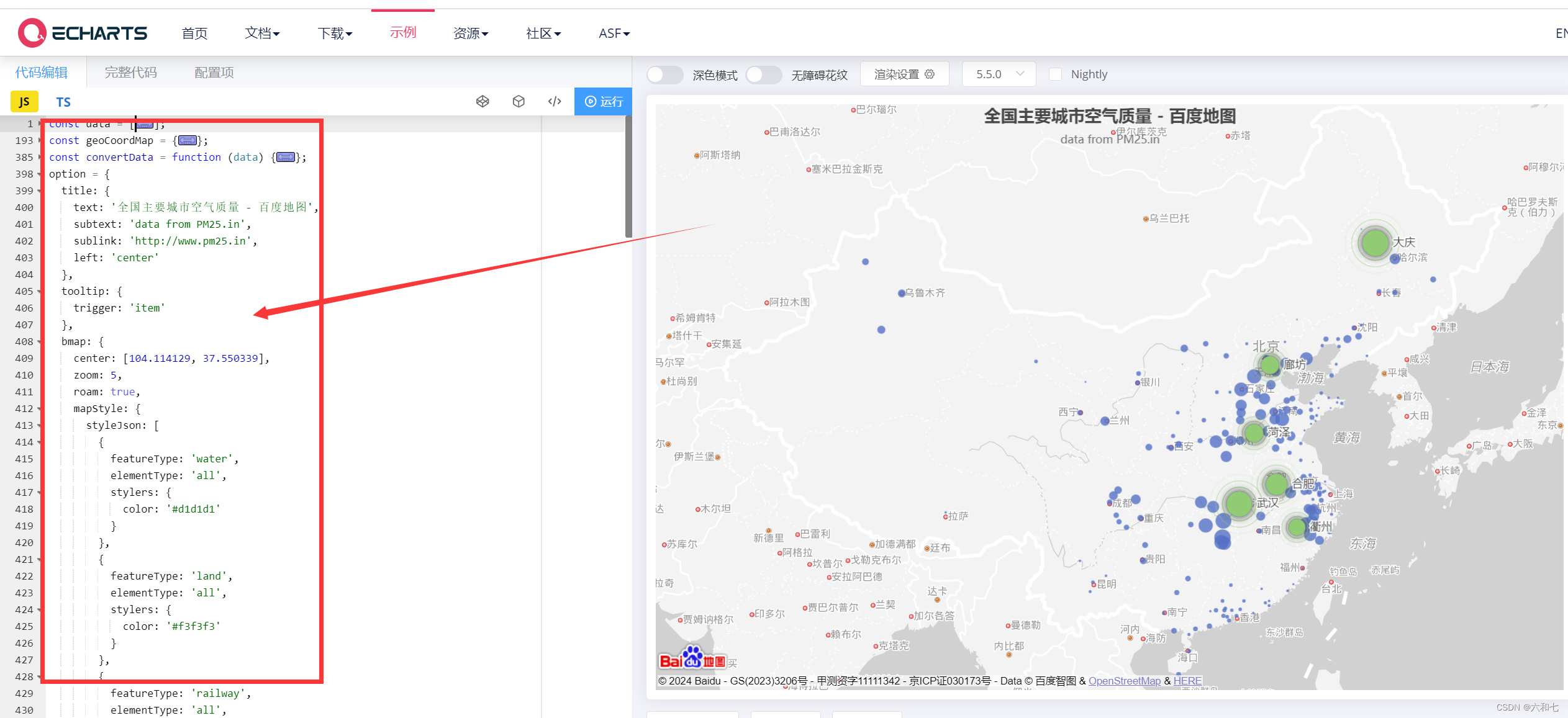
VUE3 显示Echarts百度地图
本次实现最终效果 技术基础以及环境要求 vue3 echarts 百度地图API 要求1: VUE3 环境搭建:https://blog.csdn.net/LQ_001/article/details/136293795 要求2: VUE3 echatrs 环境搭建:https://blog.csdn.net/LQ_001/article/details/1363…...

FFmpeg将视频包AVPacket通过视频流方式写入本地文件
1.写视频头 void writeVideoHeader(const char* videoFileName){int r avformat_alloc_output_context2(&pFormatCtx, nullptr, nullptr,videoFileName);if(r < 0){qDebug()<<"Error: avformat_alloc_output_context2: "<<av_err2str(r);return;…...

C语言连接【MySQL】
稍等更新图片。。。。 文章目录 安装 MySQL 库连接 MySQLMYSQL 类创建 MySQL 对象连接数据库关闭数据库连接示例 发送命令设置编码格式插入、删除或修改记录查询记录示例 参考资料 安装 MySQL 库 在 CentOS7 下,使用命令安装 MySQL: yum install mysq…...

_note_09
1.说一说类加载的过程 加载(Loading) -> 验证(Verification) -> 准备(Preparation) -> 解析(Resolution) -> 初始化(Initialization)类的加载是…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
