POS 之 最终确定性
Gasper
Casper是一种能将特定区块更新为最终确定状态的机制，使网络的新加入者确信他们正在同步规范链。当区块链出现多个分叉时，分叉选择算法使用累计投票来确保节点可以轻松选择正确的分叉。
最终确定性
最终确定性是某些区块的属性，意味着除非出现严重的共识失败，且攻击者至少销毁了总质押以太币的1/3，否则这些区块将不能回滚。 最终确定的区块可以解读为区块链是确定无疑了的。 区块必须完成两步走升级程序才能最终确定下来。
- 区块必须获得总质押以太币
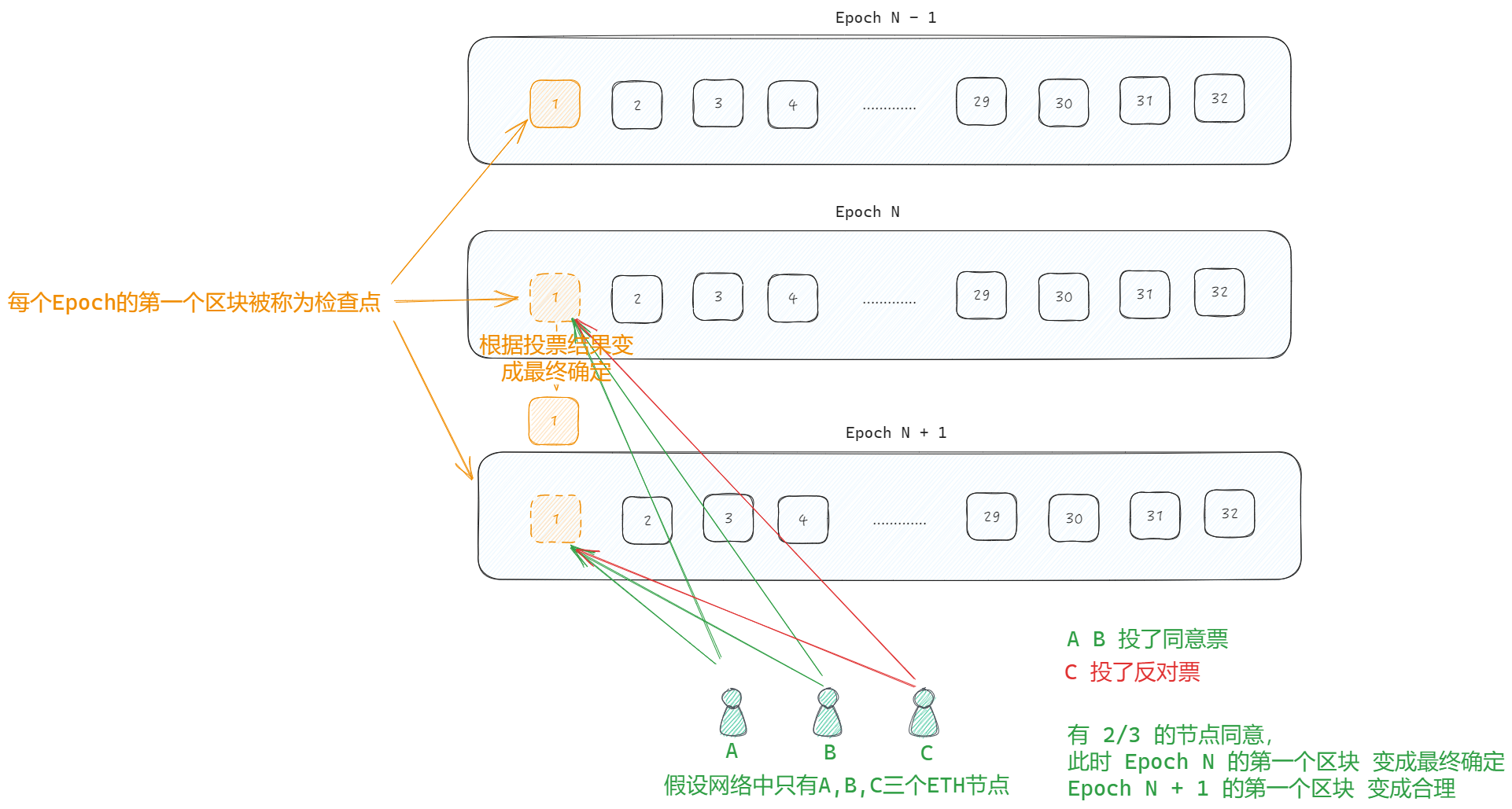
2/3的投票，才能纳入规范链（canonical chain）。 此条件可将区块升级至合理状态。 合理的区块不大可能回滚，但满足某些条件时也可以回滚。 - 每个 Epoch 的第一个区块被称为
检查点,节点会对当前Epoch 和 上一个Epoch的检查点进行投票，如果获得了质押以太币总数中三分之二以上的投票，那么上个检查点变成最终确认状态，当前检查点变成合理状态。
要
回滚最终确定的区块，攻击者将承担至少相当于质押以太币总数三分之一的损失
检查点的投票时间可能持续几个Epoch
关注我，一起进入web3的世界
相关文章：
POS 之 最终确定性
Gasper Casper 是一种能将特定区块更新为 最终确定 状态的机制，使网络的新加入者确信他们正在同步规范链。当区块链出现多个分叉时，分叉选择算法使用累计投票来确保节点可以轻松选择正确的分叉。 最终确定性 最终确定性是某些区块的属性，意味…...
Vue快速开发一个主页
前言 这里讲述我们如何快速利用Vue脚手架快速搭建一个主页。 页面布局 el-container / el-header / el-aside / el-main：https://element.eleme.cn/#/zh-CN/component/container <el-container><el-header style"background-color: #4c535a"…...
Java SE入门及基础（33）
final 修饰符 1. 应用范围 final 修饰符应该使用在类、变量以及方法上 2. final 修饰类 Note that you can also declare an entire class final. A class that is declared final cannot be subclassed. This is particularly useful, for example, when creating an imm…...
ChatGPT逐步进入留学圈但并不能解决留学规划的问题
2022 年底，一个能像人类一样对话的AI软件ChatGPT，在5天内突破一百万用户，风靡全球，如今用户已达1.8亿。 四个月后，ChatGPT进化为GPT4版本。该版本逻辑、数学推理能力卓越。拿留美标准化考试举例，GPT4能够在…...
WebGL之灯光使用解析
在使用灯光之前，首先我们需要了解，与定义更广泛的 OpenGL 不同，WebGL 并没有继承 OpenGL 中灯光的支持。所以你只能由自己完全得控制灯光。幸运得是，这也并不是很难，本文接下来就会介绍完成灯光的基础。 在 3D 空间中…...
【Spring云原生系列】SpringBoot+Spring Cloud Stream：消息驱动架构（MDA）解析，实现异步处理与解耦合
🎉🎉欢迎光临，终于等到你啦🎉🎉 🏅我是苏泽，一位对技术充满热情的探索者和分享者。🚀🚀 🌟持续更新的专栏《Spring 狂野之旅：从入门到入魔》 &a…...
PostgreSQL索引篇 | TSearch2 全文搜索
PostgreSQL版本为8.4.1 （本文为《PostgreSQL数据库内核分析》一书的总结笔记，需要电子版的可私信我） 索引篇： PostgreSQL索引篇 | BTreePostgreSQL索引篇 | GiST索引PostgreSQL索引篇 | Hash索引PostgreSQL索引篇 | GIN索引 (倒排…...
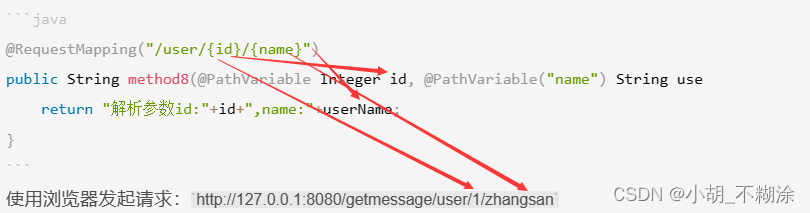
SpringMVC 中的常用注解和用法
⭐ 作者：小胡_不糊涂 🌱 作者主页：小胡_不糊涂的个人主页 📀 收录专栏：JavaEE 💖 持续更文，关注博主少走弯路，谢谢大家支持 💖 注解 1. MVC定义2. 注解2.1 RequestMappin…...
智慧城市中的数据力量：大数据与AI的应用
目录 一、引言 二、大数据与AI技术的融合 三、大数据与AI在智慧城市中的应用 1、智慧交通 2、智慧环保 3、智慧公共安全 4、智慧公共服务 四、大数据与AI在智慧城市中的价值 1、提高城市管理的效率和水平 2、优化城市资源的配置和利用 3、提升市民的生活质量和幸福感…...
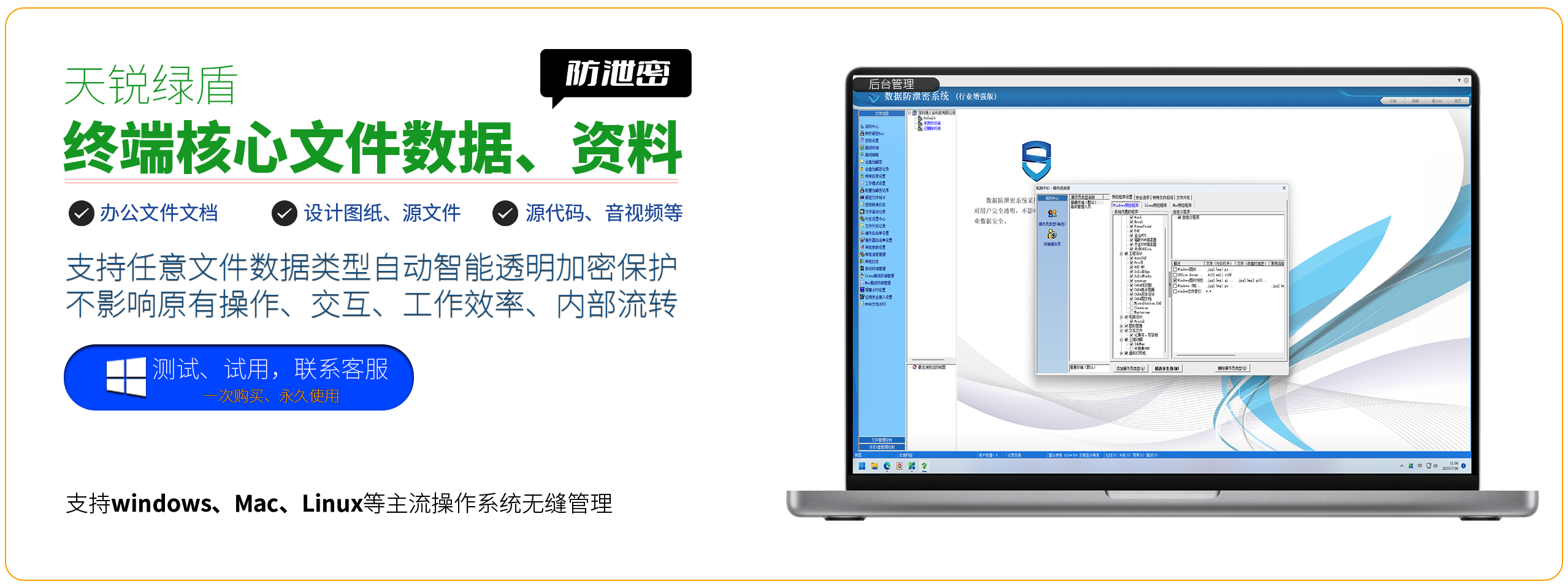
德人合科技｜天锐绿盾加密软件——数据防泄漏系统
德人合科技是一家专注于提供企业级信息安全解决方案的服务商，提供的天锐绿盾加密软件是一款专为企业设计的数据安全防护产品，主要用于解决企事业单位内部敏感数据的防泄密问题。 www.drhchina.com PC端： https://isite.baidu.com/site/wjz012…...
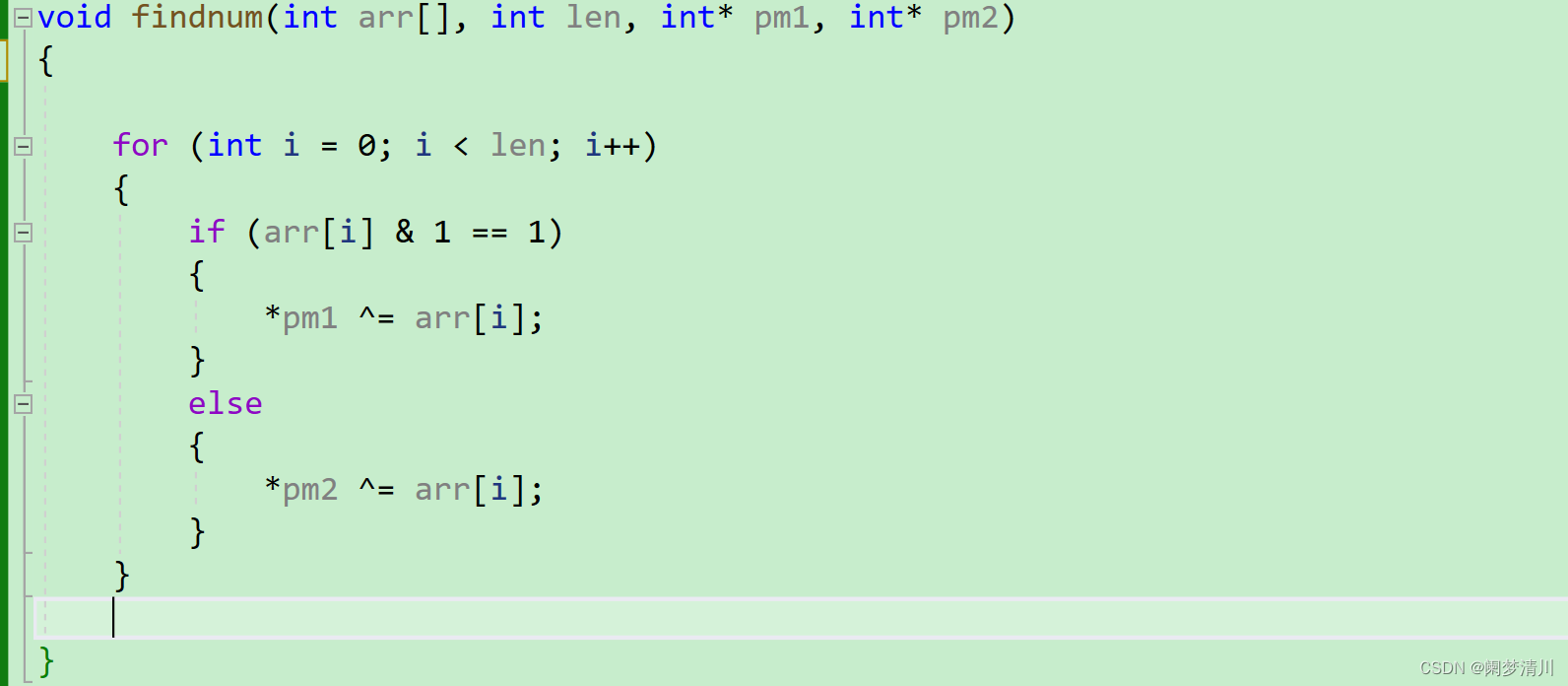
C语言---单身狗问题
1.单身狗初阶 这个题目就是数组里面有一串数字，都是成对存在的，只有一个数字只出现了一次，请你找出来 （1）异或是满足交换律的，两个相同的数字异或之后是0； （2）让0和每个…...
一次gitlab 502故障解决过程
通过top,发现prometheus进程占用CPU接近100%，这肯定有点异常。gitlab-ctl tail prometheus 发现有报错的情况，提示空间不足。暂时不管空间的问题。 2024-03-07_05:48:09.01515 ts2024-03-07T05:48:09.014Z callermain.go:1116 levelerror err"open…...
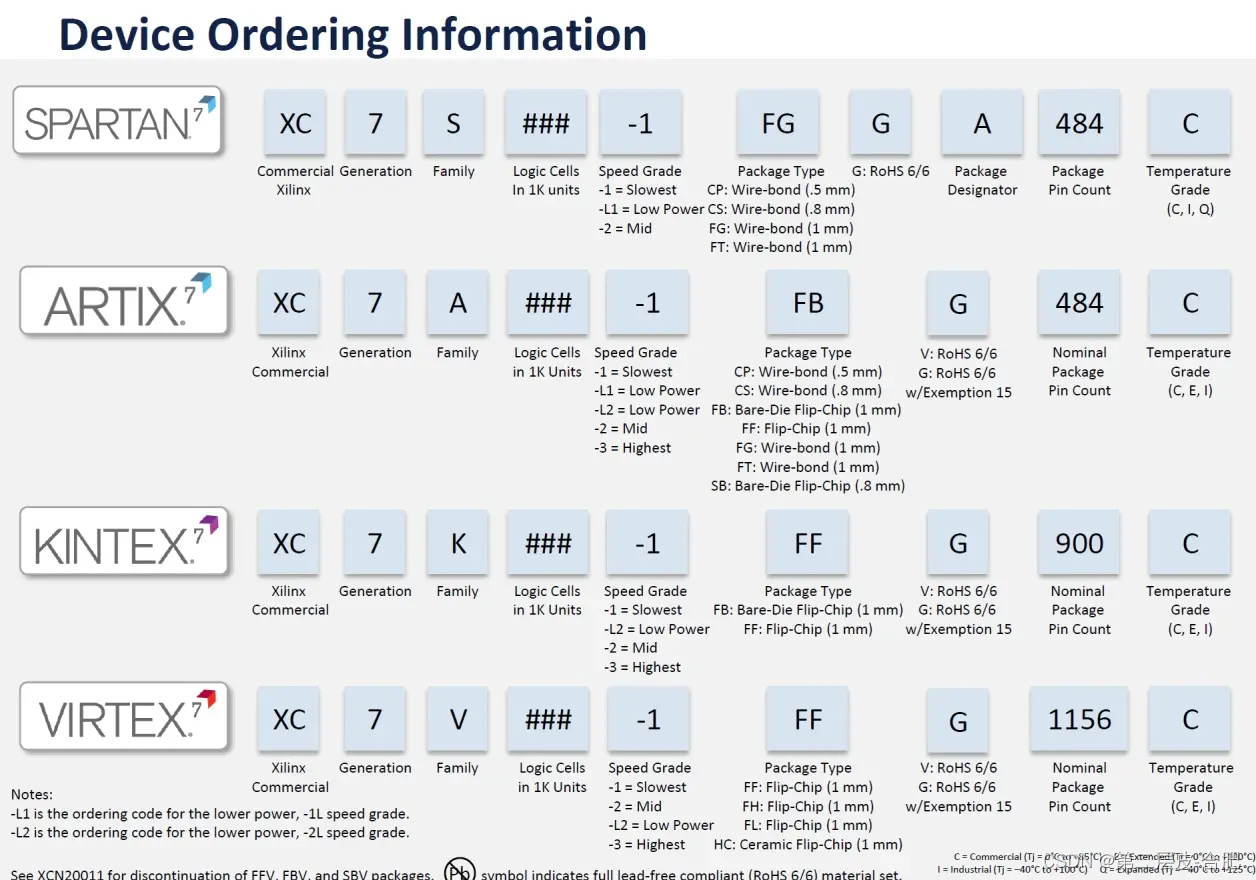
Xilinx 7系列 FPGA硬件知识系列（一）——FPGA选型参考
目录 1.1 Xilinx-7系列产品的工艺级别 编辑1.2 Xilinx-7系列产品的特点 1.2.1 Spartan-7系列 1.2.2 Artix-7系列 1.2.3 Kintex-7系列 1.2.4 Virtex-7系列 1.3 Xilinx-7系列FPGA对比 1.3.1 DSP资源柱状图 1.3.2 Block RAM资源柱状图 1.3.3 高速串行收…...
【C++从练气到飞升】02---初识类与对象
🎈个人主页：库库的里昂 ✨收录专栏：C从练气到飞升 🎉鸟欲高飞先振翅，人求上进先读书。 目录 ⛳️推荐 一、面向过程和面向对象初步认识 二、类的引用 1. C语言版 2. C版 三、类的定义 类的两种定义方式ÿ…...
探秘分布式神器RMI：原理、应用与前景分析（一）
本系列文章简介： 本系列文章将深入探究RMI远程调用的原理、应用及未来的发展趋势。首先，我们会详细介绍RMI的工作原理和基本流程，解析其在分布式系统中的核心技术。随后，我们将探讨RMI在各个领域的应用，包括分布式计算…...
JVM（Java虚拟机）概述
1. JVM的定义和作用 JVM（Java Virtual Machine）是一个能够运行Java字节码的虚拟计算机。它是Java平台的核心组成部分，负责执行编译后的Java程序，提供跨平台运行的能力。JVM使得Java程序可以在任何安装了JVM的操作系统上运行&#…...
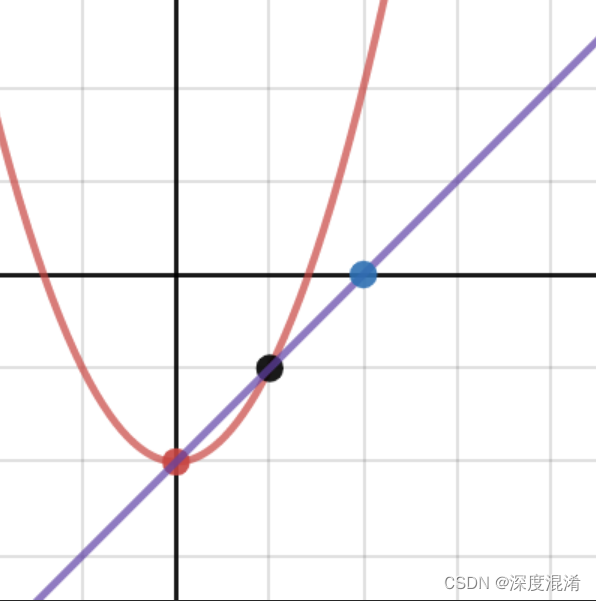
C#，数值计算，用割线法（Secant Method）求方程根的算法与源代码
1 割线法 割线法用于求方程 f(x) 0 的根。它是从根的两个不同估计 x1 和 x2 开始的。这是一个迭代过程，包括对根的线性插值。如果两个中间值之间的差值小于收敛因子，则迭代停止。 亦称弦截法，又称线性插值法.一种迭代法.指用割线近似曲线求…...
HTML静态网页成品作业(HTML+CSS)——花主题介绍网页设计制作(1个页面)
🎉不定期分享源码，关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS，未使用Javacsript代码，共有1个页面。 二、作品演示 三、代…...
Keepalive 解决nginx 的高可用问题
一 说明 keepalived利用 VRRP Script 技术，可以调用外部的辅助脚本进行资源监控，并根据监控的结果实现优先动态调整，从而实现其它应用的高可用性功能 参考配置文件： /usr/share/doc/keepalived/keepalived.conf.vrrp.localche…...
DPN网络
DPN DPN（Dual Path Networks）是一种网络结构，它结合了DensNet和ResNetXt两种思想的优点。这种结构的目的是通过不同的路径来利用神经网络的不同特性，从而提高模型的效率和性能。 DenseNet 的特点是其稠密连接路径，使…...
Python｜GIF 解析与构建（5）：手搓截屏和帧率控制
目录 Python｜GIF 解析与构建（5）：手搓截屏和帧率控制 一、引言 二、技术实现：手搓截屏模块 2.1 核心原理 2.2 代码解析：ScreenshotData类 2.2.1 截图函数：capture_screen 三、技术实现&…...
linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源（HTML/CSS/图片等），响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址，提高安全性 3.负载均衡服务器 支持多种策略分发流量…...
Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题： 下面创建一个简单的Flask RESTful API示例。首先，我们需要创建环境，安装必要的依赖，然后…...
大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动（如演唱会、马拉松赛事、高考中考等）期间，城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例，暖城商圈曾因观众集中离场导致周边…...
鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建： 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建： File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...
django filter 统计数量 按属性去重
在Django中，如果你想要根据某个属性对查询集进行去重并统计数量，你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求： 方法1：使用annotate()和Count 假设你有一个模型Item，并且你想…...
1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件，然后打开终端，进入下载文件夹，键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...
《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术，说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号（调制） 把信息从信号中抽取出来&am…...
微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
【Web 进阶篇】优雅的接口设计：统一响应、全局异常处理与参数校验
系列回顾： 在上一篇中，我们成功地为应用集成了数据库，并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了！但是，如果你仔细审视那些 API，会发现它们还很“粗糙”：有…...