C#,数值计算,用割线法(Secant Method)求方程根的算法与源代码

1 割线法
割线法用于求方程 f(x) = 0 的根。它是从根的两个不同估计 x1 和 x2 开始的。这是一个迭代过程,包括对根的线性插值。如果两个中间值之间的差值小于收敛因子,则迭代停止。
亦称弦截法,又称线性插值法.一种迭代法.指用割线近似曲线求方程根的2步迭代法.此法用通过点(xk,f(xk))及(xk-1,f(xk-1))的割线

近似曲线y=f(x),用割线的根作为方程根的新近似xk+1,从而得到方程求根的割线法迭代程序

( k=1,2,…,n),
其中x0,x1为初始近似.若f(x)在根x*的邻域内有二阶连续导数,且f′(x*)≠0,则当x0,x1在x*邻域内时,割线法收敛于x*,其收敛阶为


2 源程序
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public delegate double delegateFunctionX(double x);
public static partial class Algorithm_Gallery
{
public static delegateFunctionX funx = null;
public static bool Secant(double x1, double x2, out double x0, double Epsilon)
{
int n = 0;
double xm;
x0 = x1;
if (funx(x1) * funx(x2) < 0)
{
do
{
x0 = (x1 * funx(x2) - x2 * funx(x1)) / (funx(x2) - funx(x1));
double c = funx(x1) * funx(x0);
x1 = x2;
x2 = x0;
n++;
if (Math.Abs(c) < float.Epsilon)
{
break;
}
xm = (x1 * funx(x2) - x2 * funx(x1)) / (funx(x2) - funx(x1));
} while (Math.Abs(xm - x0) >= Epsilon);
return true;
}
else
{
return false;
}
}
}
}
3 源代码
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;namespace Legalsoft.Truffer.Algorithm
{public delegate double delegateFunctionX(double x);public static partial class Algorithm_Gallery{public static delegateFunctionX funx = null;public static bool Secant(double x1, double x2, out double x0, double Epsilon){int n = 0;double xm;x0 = x1;if (funx(x1) * funx(x2) < 0){do{x0 = (x1 * funx(x2) - x2 * funx(x1)) / (funx(x2) - funx(x1));double c = funx(x1) * funx(x0);x1 = x2;x2 = x0;n++;if (Math.Abs(c) < float.Epsilon){break;}xm = (x1 * funx(x2) - x2 * funx(x1)) / (funx(x2) - funx(x1));} while (Math.Abs(xm - x0) >= Epsilon);return true;}else{return false;}}}
}
相关文章:

C#,数值计算,用割线法(Secant Method)求方程根的算法与源代码
1 割线法 割线法用于求方程 f(x) 0 的根。它是从根的两个不同估计 x1 和 x2 开始的。这是一个迭代过程,包括对根的线性插值。如果两个中间值之间的差值小于收敛因子,则迭代停止。 亦称弦截法,又称线性插值法.一种迭代法.指用割线近似曲线求…...

HTML静态网页成品作业(HTML+CSS)——花主题介绍网页设计制作(1个页面)
🎉不定期分享源码,关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 🏷️本套采用HTMLCSS,未使用Javacsript代码,共有1个页面。 二、作品演示 三、代…...

Keepalive 解决nginx 的高可用问题
一 说明 keepalived利用 VRRP Script 技术,可以调用外部的辅助脚本进行资源监控,并根据监控的结果实现优先动态调整,从而实现其它应用的高可用性功能 参考配置文件: /usr/share/doc/keepalived/keepalived.conf.vrrp.localche…...

DPN网络
DPN DPN(Dual Path Networks)是一种网络结构,它结合了DensNet和ResNetXt两种思想的优点。这种结构的目的是通过不同的路径来利用神经网络的不同特性,从而提高模型的效率和性能。 DenseNet 的特点是其稠密连接路径,使…...
循序渐进丨MogDB 数据库新特性之SQL PATCH绑定执行计划
1 SQL PATCH 熟悉 Oracle 的DBA都知道,生产系统出现性能问题时,往往是SQL走错了执行计划,紧急情况下,无法及时修改应用代码,DBA可以采用多种方式针对于某类SQL进行执行计划绑定,比如SQL Profile、SPM、SQL …...

【论文阅读随笔】RoPE/旋转编码:ROFORMER: ENHANCED TRANSFORMER WITH ROTARY POSITION EMBEDDING
文章目录 1.目的:通过绝对位置编码的方式实现相对位置编码2.理解RoPE,在我看来有几个需要注意的点:3.本文相关复数概念:3.1.复数乘法的几何意义3.2.复数内积 VS. 复数乘法 4.REF: 1.目的:通过绝对位置编码的…...

数据挖掘
一.数据仓库概述: 1.1数据仓库概述 1.1.1数据仓库定义 数据仓库是一个用于支持管理决策的、面向主题、集成、相对稳定且反映历史变化的数据集合。 1.1.2数据仓库四大特征 集成性(Integration): 数据仓库集成了来自多个不同来源…...
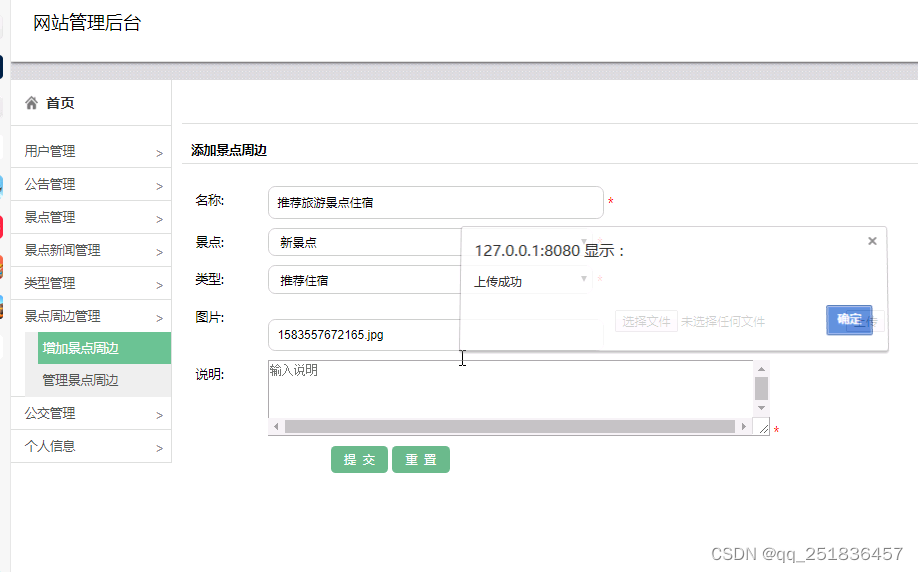
java SSM旅游景点与公交线路查询系统myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 java SSM旅游景点与公交线路查询系统是一套完善的web设计系统(系统采用SSM框架进行设计开发,springspringMVCmybatis),对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系…...

解决Git报错:fatal: detected dubious ownership in repository at
在通过 Git Bash 提交项目代码时输入 git add . 命令后,报错:fatal: detected dubious ownership in repository at 这是因为该项目的所有者与现在的用户不一致 比如说: 该项目的所有者是 Administrator,而当前用户是 YuYang, 那…...
网络协议常见问题
网络协议常见问题 OSI(Open Systems Interconnection)模型OSI 封装 TCP/IP协议栈IP数据报的报头TCP头格式UDP头格式TCP (3-way shake)三次握手建立连接:为什么三次握手才可以初始化 Socket、序列号和窗口大小并建立 TCP 连接。每次建立TCP连接…...

人工智能的迷惑行为
目录 前言1 人工智能的“幽默”瞬间1.1 语义误解1.2 逻辑错误 2 技术原理探究2.1 算法设计缺陷2.2 数据处理不当 3 社会影响分析3.1 信任度下降3.2 技术担忧 结语 前言 随着人工智能技术的迅猛发展,各类AI大模型如ChatGPT、文心一言、通义千问等纷纷登场࿰…...

XR技术:短剧制作的全新纪元
在数字技术的浪潮中,XR(扩展现实)技术以其独特的魅力,正在为短剧制作带来革命性的突破。这种融合了虚拟现实、增强现实和混合现实等先进技术的创新工具,正逐渐改变着短剧制作的传统模式,引领着短剧艺术走向…...
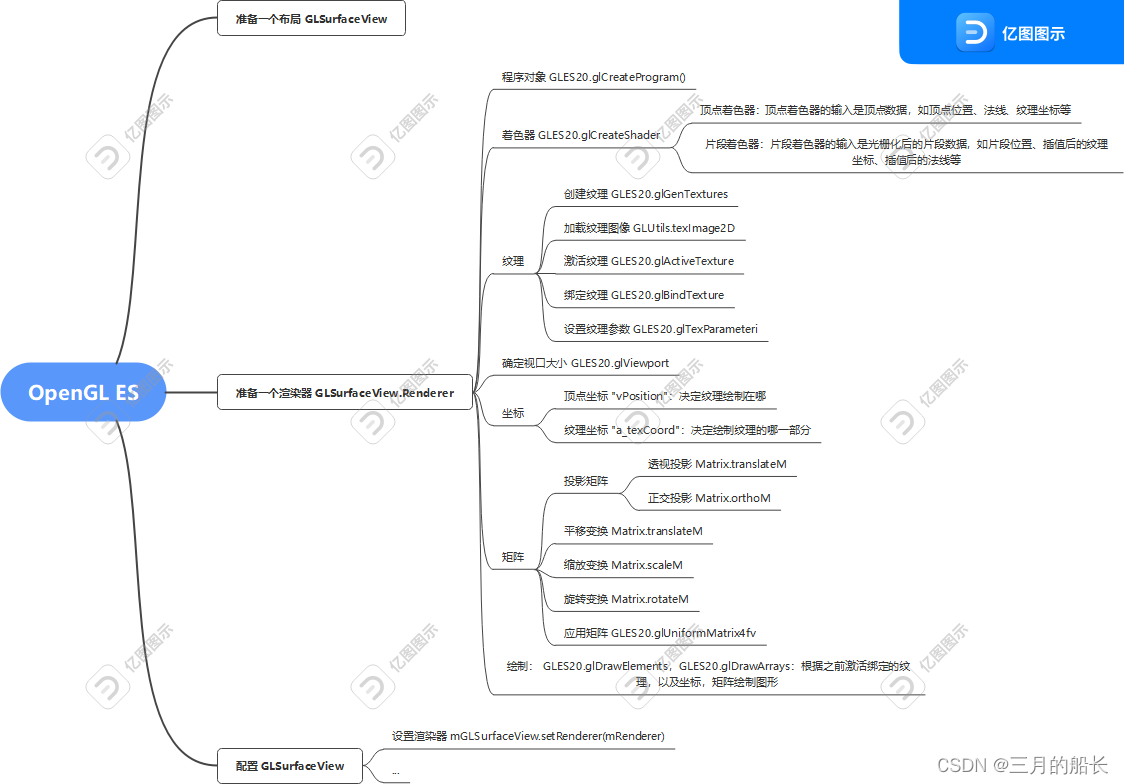
安卓 OpenGL ES 学习笔记
文章目录 OpenGL 学习笔记OpenGL 是什么?OpenGL ES是什么?怎么用?hello world如何实现动画效果 参考文章 OpenGL 学习笔记 OpenGL 是什么? OpenGL(Open Graphics Library)是一个跨平台的图形编程接口&…...

git分布式管理-头歌实验冲突处理、忽略文件
一、解决冲突 任务描述 在团队协作开发过程中,可能你和团队中的其他成员,都修改了某个文件的某一部分内容,且其他成员已将该修改推送到了远程仓库。这样当你需要合并他的代码的时候,可能就会在内容上出现冲突,这个时候…...

【实战项目】网络编程:在Linux环境下基于opencv和socket的人脸识别系统--C++实现
🌞前言 这里我们会实现一个项目:在linux操作系统下基于OpenCV和Socket的人脸识别系统。 目录 🌞前言 🌞一、项目介绍 🌞二、项目分工 🌞三、项目难题 🌞四、实现细节 🌼4.1 关…...

零售EDI:劳氏 Lowe‘s EDI项目案例
通过 EDI,企业与Lowes之间可以直接交换各种商业文档,如订单、发票、收据等,从而实现信息的实时交换,提高了供应链的效率和准确性。在现代供应链管理中,EDI 已经成为了不可或缺的重要工具。 作为一家拥有多条业务线的企…...
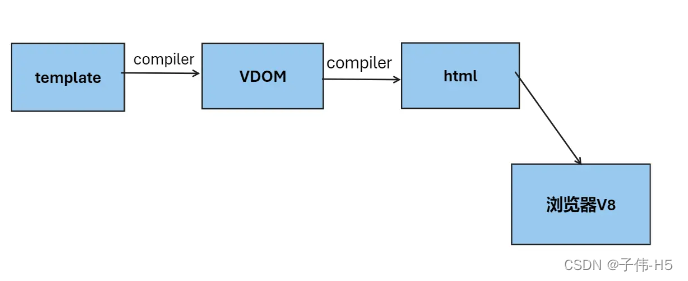
为什么不用 index 做 key?
“在 Vue 中,我们在使用 v-for 渲染列表的时候,为什么要绑定一个 key?能不能用 index 做 key?” 在聊这个问题之前我们还得需要知道 Vue 是如何操作 DOM 结构的。 虚拟DOM 我们知道,Vue 不可以直接操作 DOM 结构&am…...
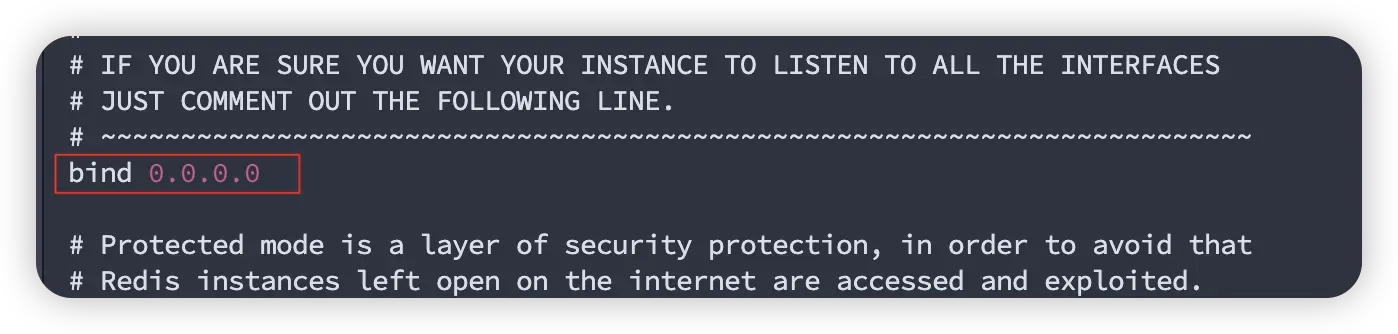
Linux虚拟机安装Redis
官网下载压缩包:官网链接,然后将对应的tar.gz压缩包放入虚拟机下的/opt目录下。由于redis是C语言开发的,因此需要安装gcc编译器来编译代码,我们下载的压缩包里面是源代码,需要编译。通过yum install gcc指令下载C语言的…...

网络安全: Kali Linux 进行 SSH 渗透与防御
目录 一、实验 1.环境 2.nmap扫描目标主机 3.Kali Linux 进行 SSH 渗透 3.Kali Linux 进行 SSH 防御 二、问题 1.SSH有哪些安全配置 一、实验 1.环境 (1)主机 表1 主机 系统版本IP备注Kali Linux2022.4 192.168.204.154(动态&…...

近年来文本检测相关工作梳理
引言 场景文本检测任务,一直以来是OCR整个任务中最为重要的一环。虽然有一些相关工作是端对端OCR工作的,但是从工业界来看,相关落地应用较为困难。因此,两阶段的OCR方案一直是优先考虑的。 在两阶段中(文本检测文本识…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...
