算法D39 | 动态规划2 | 62.不同路径 63. 不同路径 II
今天开始逐渐有 dp的感觉了,题目不多,就两个 不同路径,可以好好研究一下
62.不同路径
本题大家掌握动态规划的方法就可以。 数论方法 有点非主流,很难想到。
代码随想录
视频讲解:动态规划中如何初始化很重要!| LeetCode:62.不同路径_哔哩哔哩_bilibili
这个题看到路径的表示,第一直觉就是一个组合数的问题,学了一下C++计算组合数防止溢出的小技巧。第二个方法再动态规划完成, 重点是把二维的动态规划dp[i][j]表示清楚,从左右到从上到下的顺序遍历就行。
Python数论:
class Solution:def uniquePaths(self, m: int, n: int) -> int:if m==1 or n==1: return 1total = m + n -2if m>n: m, n = n, mnom = denom = 1for i in range(m-1):nom *= (total-i)denom *= (i+1)result = int(nom/denom)return resultC++数论:
C++计算组合数需要考虑溢出的问题,long long int并不能通过所有的case,那么修改数据容量就不是个完备的解决方案了。优化的基本思路是连续m个整数相乘,一定能将m整除。
为了防止溢出,从小到大考虑,而不是从大到小(n到n-m+1, m到1)。
另外,确保m<=n的操作下,确保了m!比 n!/(n-m)!小。
主要参考组合数的计算(对溢出处理)_long long int 放不下-CSDN博客
class Solution {
public:int uniquePaths(int m, int n) {if (m==1 || n==1) return 1;if (m>n) {int tmp = n;n = m;m = tmp;}long long sum = 1;for (int i=1; i<m; i++) {sum *= m+n-1-i;sum /= i;}return sum;}
};Python动态规划:
class Solution:def uniquePaths(self, m: int, n: int) -> int:if m==1 or n==1: return 1dp = [[0]*n for _ in range(m)]for i in range(1, m):for j in range(1, n):if i==1:dp[i-1][j] = 1if j==1:dp[i][j-1] = 1dp[i][j] = dp[i-1][j] + dp[i][j-1]return dp[m-1][n-1]C++动态规划:
class Solution {
public:int uniquePaths(int m, int n) {if (m==1 || n==1) return 1;vector<vector<int>> dp(m, vector<int>(n, 0));for (int i=1; i<m; i++) {for (int j=1; j<n; j++) {if (i==1) dp[i-1][j] = 1;if (j==1) dp[i][j-1] = 1;dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m-1][n-1];}
};63. 不同路径 II
https://programmercarl.com/0063.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84II.htmlhttps://programmercarl.com/0063.%E4%B8%8D%E5%90%8C%E8%B7%AF%E5%BE%84II.html
视频讲解:动态规划,这次遇到障碍了| LeetCode:63. 不同路径 II_哔哩哔哩_bilibili
有障碍的这个变形数论就没那么适合了,动态规划遍历更合适一些。
Python:
class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:m = len(obstacleGrid)n = len(obstacleGrid[0])dp = [[0]*n for _ in range(m)]i = j = 0while i<m and obstacleGrid[i][0]==0:dp[i][0] = 1i+=1while j<n and obstacleGrid[0][j]==0:dp[0][j] = 1 j+=1for i in range(1, m):for j in range(1, n):if obstacleGrid[i][j] == 0:dp[i][j] = dp[i-1][j] + dp[i][j-1]return dp[m-1][n-1]C++:
C++版本初始化dp表格时,不能用while实现,用forloop也可以提前终止,代码更简洁一些。
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();if (obstacleGrid[0][0]==1 || obstacleGrid[m-1][n-1]==1) return 0;vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;for (int i=1; i<m; i++) {for (int j=1; j<n; j++) {if (obstacleGrid[i][j]==0) dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m-1][n-1];}
};相关文章:

算法D39 | 动态规划2 | 62.不同路径 63. 不同路径 II
今天开始逐渐有 dp的感觉了,题目不多,就两个 不同路径,可以好好研究一下 62.不同路径 本题大家掌握动态规划的方法就可以。 数论方法 有点非主流,很难想到。 代码随想录 视频讲解:动态规划中如何初始化很重要&#x…...

面试官:如何在 Spring Boot 启动的时候提前运行一些特定的代码
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:如何在 Spring Boot 启动的时候提前运行一些特定的代码 在Spring Boot启动的时候提前运行一些特定的代码可以通过实现ApplicationRunner接口、Com…...
力扣最热100题——56.合并区间
吾日三省吾身 还记得梦想吗 正在努力实现它吗 可以坚持下去吗 目录 吾日三省吾身 力扣题号:56. 合并区间 - 力扣(LeetCode) 题目描述 Java解法一:排序然后原地操作 具体代码如下 Java解法二:new一个list…...

docker学习(十四)docker搭建私服
docker私服搭建,配置域名访问,设置访问密码 启动registry docker run -d \-p 5000:5000 \-v /opt/data/registry:/var/lib/registry \registrydocker pull hello-world docker tag hello-world 127.0.0.1:5000/hello-world docker push 127.0.0.1:5000…...

基于BERTopic模型的英文20新闻数据集主题聚类及可视化
文章目录 bertopic介绍20 newsgroups dataset20 newsgroups数据集下载数据导入nltk数据处理bertopic模型构建模型训练运行模型可视化目前主题的一致性得分语料库建模bertopic介绍 BERTopic 是基于深度学习的一种主题建模方法。BERT 是一种用于 NLP 的预训练策略,它成功地利用…...

【Oracle之DataGuard的初步学习】
** 以下所有均是基于11G版本的 ** 一、DataGuard的部署方式 DG的部署最常用的方式就是直接在备库端部署一个空库然后再设置参数,但是这样做在初始同步时如果数据量过大会耗费较长的时间;相对来说这中方式比较简单不易出错。 还有一种方式就是通过rman的备…...
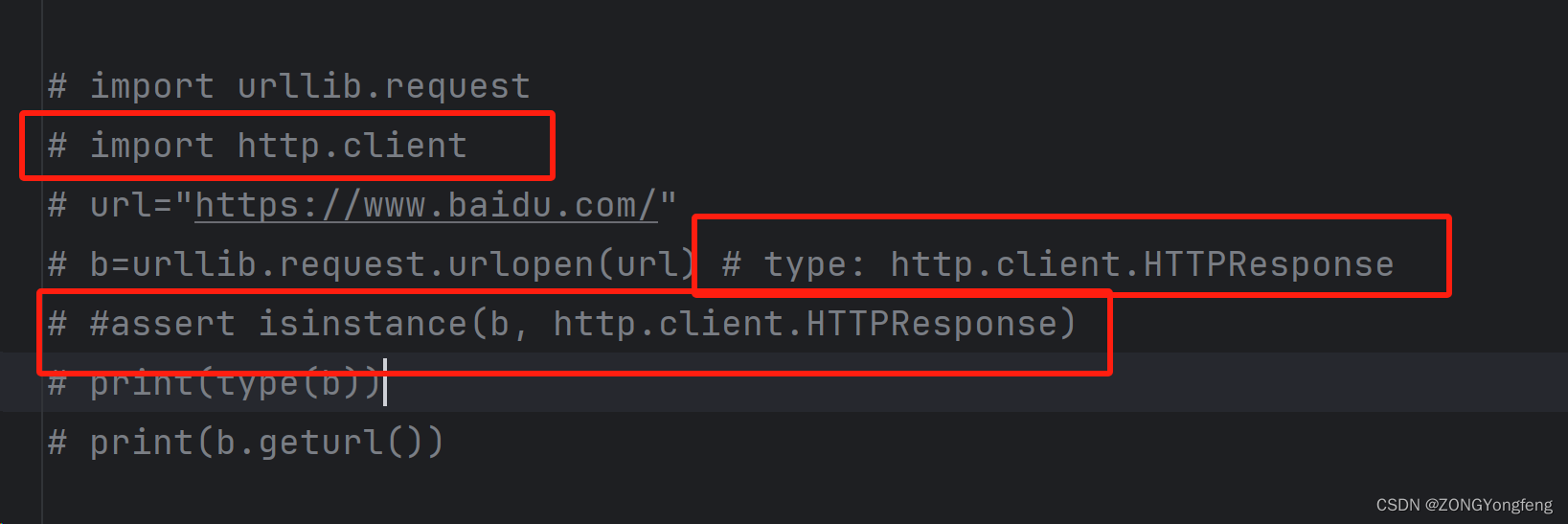
PyCharm无代码提示解决
PyCharm无代码提示解决方法 在使用PyCharm工具时,调用方法却无法进行提示,针对PyCharm无代码提示整理下解决方案 1、Python内置语法无智能提示 复现:我这里以urllib库读取网页内容为例,在通过urlopen()之后调用getur…...
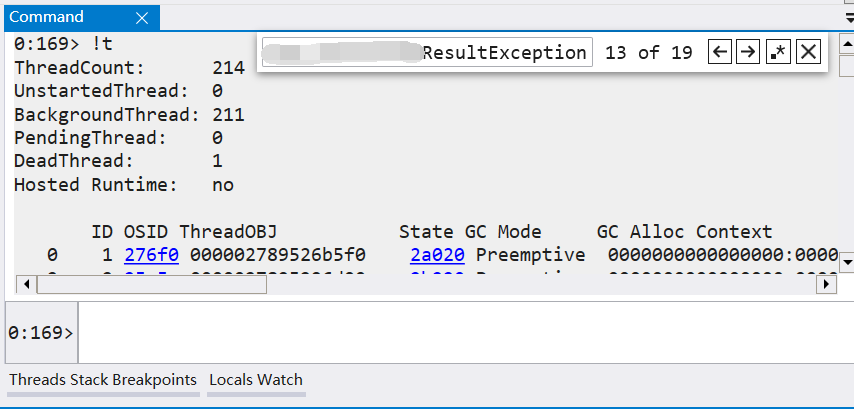
记一次 .NET某设备监控自动化系统 CPU爆高分析
一:背景 1. 讲故事 先说一下题外话,一个监控别人系统运行状态的程序,结果自己出问题了,有时候想一想还是挺讽刺的,哈哈,开个玩笑,我们回到正题,前些天有位朋友找到我,说…...

大数据与云计算
目录 一、大数据时代二、云计算——大数据的计算三、云计算发展现状四、云计算实现机制五、云计算压倒性的成本优势 一、大数据时代 我们先来看看百度关于 “大数据”(Big Data)的搜索指数。 可以看出,“大数据” 这个词是从2012年才引起关注…...

一. 并行处理与GPU体系架构-并行处理简介
目录 前言0. 简述1. 串行处理与并行处理的区别2. 并行执行3. 容易混淆的几个概念4. 常见的并行处理总结参考 前言 自动驾驶之心推出的 《CUDA与TensorRT部署实战课程》,链接。记录下个人学习笔记,仅供自己参考 本次课程我们来学习下课程第一章——并行处…...

vb机试考试成绩分析与统计,设计与实现(高数概率统计)-141-(代码+程序说明)
转载地址http://www.3q2008.com/soft/search.asp?keyword141 前言: 为何口出狂言,作任何VB和ASP的系统, 这个就是很好的一个证明 :) 又有些狂了... 数据库操作谁都会,接触的多了也没什么难的,VB编程难在哪?算法上,这个是一个算法题的毕业设计,里面涉及到对试卷的 平均分,最…...
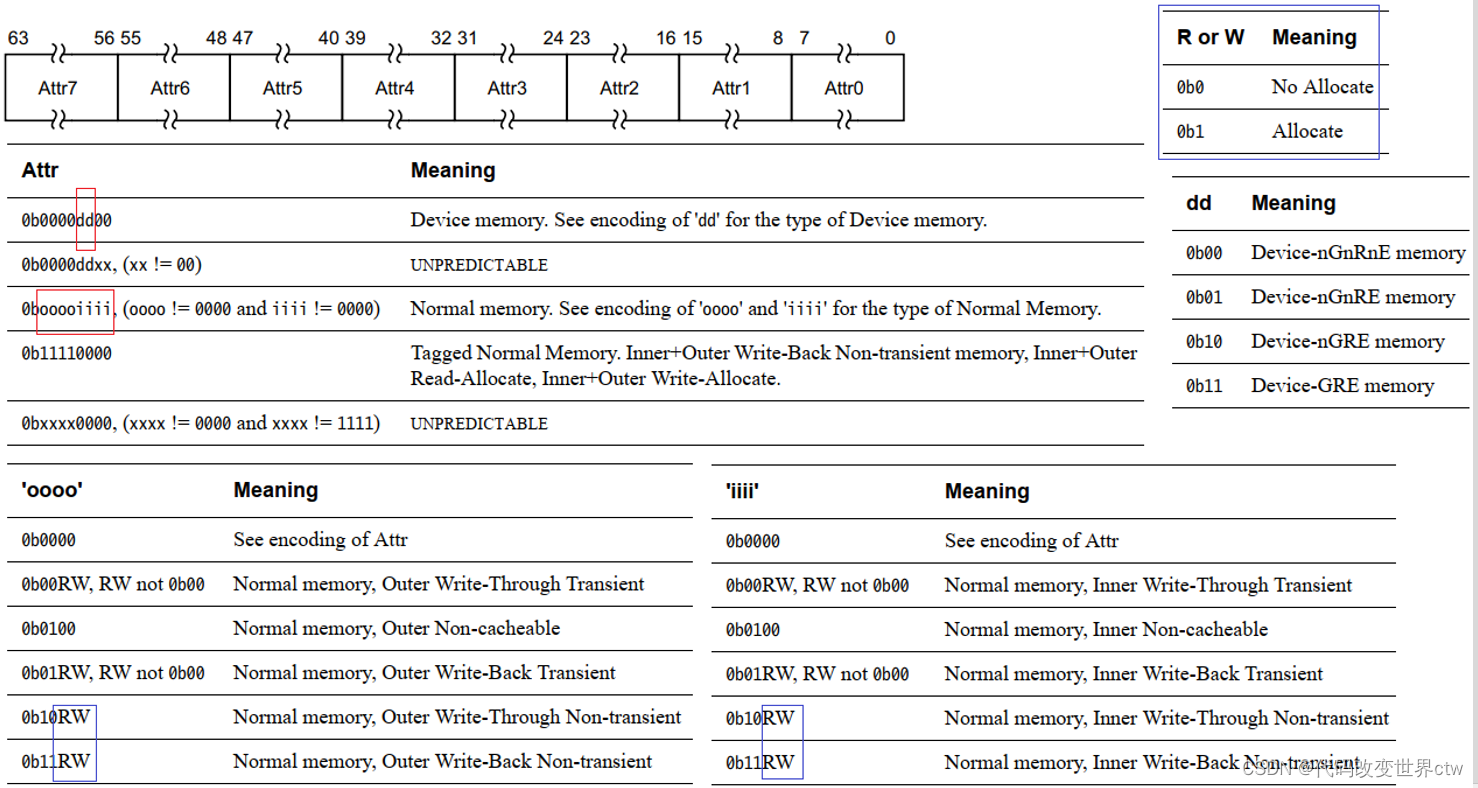
Arm MMU深度解读
文章目录 一、MMU概念介绍二、虚拟地址空间和物理地址空间2.1、(虚拟/物理)地址空间的范围2.2、物理地址空间有效位(范围) 三、Translation regimes四、地址翻译/几级页表?4.1、思考:页表到底有几级?4.2、以4KB granule为例,页表的…...

2024 年 AI 辅助研发趋势
在2024年,AI辅助研发的应用趋势将非常广泛。举个例子,比如在医疗健康领域,AI将深度参与新药研发、早期癌症研究以及辅助诊断等,助力医疗技术的突破。同时,在农业领域,AI也将通过无人机、智能装备等方式&…...

聊聊pytho中的函数
Python中的函数 一、Python中函数的作用与使用步骤 1、为什么需要函数 在Python实际开发中,我们使用函数的目的只有一个“让我们的代码可以被重复使用” 函数的作用有两个: ① 代码重用(代码重复使用) ② 模块化编程&#x…...

Python中starmap有什么用的?
目录 前言 starmap函数的作用 starmap函数的用法 starmap函数的示例 1. 对每个元组元素进行求和 2. 对每个元组元素进行乘积 实际应用场景 1. 批量处理函数参数 2. 并行处理任务 3. 批量更新数据库 总结 前言 在Python中, starmap 是一个非常有用的函数&…...
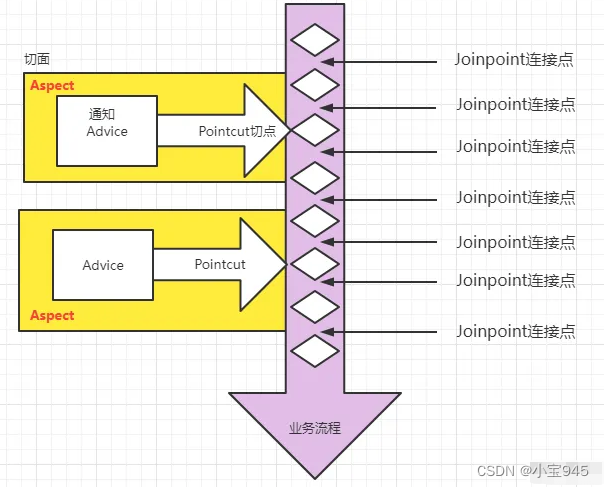
面向切面编程 AOP
提示:主要内容参考动力节点老杜的Spring6讲义。 面向切面编程 AOP 一、AOP介绍二、AOP的七大术语三、切点表达式 IoC使软件组件松耦合。AOP让你能够捕捉系统中经常使用的功能,把它转化成组件。AOP(Aspect Oriented Programming)&a…...

POS 之 奖励机制
为什么需要有奖惩机制 如果没有奖励,就不会有节点参与POS,运营节点有成本,而奖励正是让运营者获利的方式 如果没有惩罚,网络上会充斥着很多无效节点,会扰乱甚至破坏网络 所有奖励和惩罚在每个 Epoch 实施一次 奖励 什…...

Unity类银河恶魔城学习记录9-7 p88 Crystal instead of Clone源代码
Alex教程每一P的教程原代码加上我自己的理解初步理解写的注释,可供学习Alex教程的人参考 此代码仅为较上一P有所改变的代码 【Unity教程】从0编程制作类银河恶魔城游戏_哔哩哔哩_bilibili Blackhole_Skill_Controller.cs using System.Collections; using System…...

导出RWKV模型为onnx
测试模型: https://huggingface.co/RWKV/rwkv-5-world-3b 导出前对modeling_rwkv5.py进行一个修改: # out out.reshape(B * T, H * S) out out.reshape(B * T, H * S, 1) # <<--- modified out F.group_norm(out, nu…...
)
【LeetCode】整数转罗马数字 C语言 | 此刻,已成艺术(bushi)
Problem: 12. 整数转罗马数字 文章目录 思路解题方法复杂度Code 思路 暴力破解 转换 解题方法 由思路可知 复杂度 时间复杂度: O ( n ) O(n) O(n) 空间复杂度: O ( 1 ) O(1) O(1) Code char* intToRoman(int num) {char *s (char*)malloc(sizeof(char)*4000), *p s;while(…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...
