四节点/八节点四边形单元悬臂梁Matlab有限元编程 | 平面单元 | Matlab源码 | 理论文本
专栏导读
- 作者简介:工学博士,高级工程师,专注于工业软件算法研究
- 本文已收录于专栏:《有限元编程从入门到精通》本专栏旨在提供 1.以案例的形式讲解各类有限元问题的程序实现,并提供所有案例完整源码;2.单元类型包含:杆单元,梁单元,平面三角形单元,薄板单元,厚板单元,壳单元,四/六面体实体单元,金字塔单元等;3.物理场问题涉及:力学、传热学、电磁学及多物理场耦合等问题的稳态(静力学)和瞬态(动力学)求解。专栏旨在帮助有志于有限元工业软件开发的小伙伴,快速上手有限元编程,在案例中成长,摆脱按部就班填鸭式教学。
- 【所有专栏文章均提供对应视频课】,文本教程+视频教程,双向强化学习!
- 欢迎订阅专栏,订阅用户可私聊进入有限元编程交流群(知识交流、问题解答),并获赠丰厚的有限元相关学习资料(教材、源码、视频课)
- 专栏订阅地址:有限元编程从入门到精通_suoge223的博客-CSDN博客
文章目录
专栏导读
文章目录
【总体简介】💻🔍
【代码截图】
【文本教程截图】
【视频教程】
【总体简介】💻🔍
代码以受均布荷载和集中荷载的变截面悬臂梁为研究对象,通过matlab编制四节点和八节点四边形单元有限元程序来对悬臂梁进行受力分析。核心理论基础请参考博文《四节点/八节点四边形单元悬臂梁Matlab有限元编程》。
你将获得:四节点/八节点四边形单元的有限元matlab程序源码+程序理论文本doc文件
获取链接:四面体单元悬臂梁的Matlab有限元编程 | 实体单元 | Matlab源码 | 理论文本
一、问题概述
如图 所示,某变截面悬臂梁长度为2m,截面面积由0.6m至0.2m线性变化,受作用在自由端节点的集中荷载2P=kN和竖直方向均布荷载q=1kN/m作用,按平面应力问题分析,求解自由端节点挠度。变截面悬臂梁采用C30混凝土,弹性模量为E= 4 3 10 MPa,泊松比为。编制四节点和八节点四边形单元有限元程序,最终得到梁的变形。
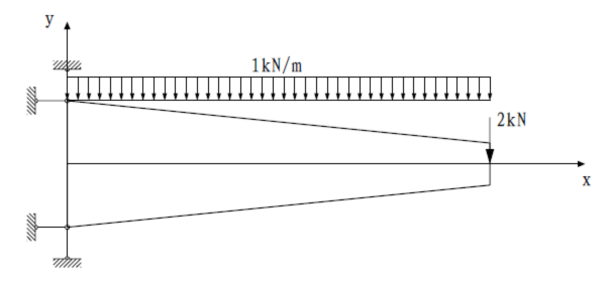
代码运行效果

二、求解思路
对于本问题采用基于MATLAB 编制有限元分析程序进行求解,其基本组成部分包括前处理模块、分析主程序模块和后处理模块。在前处理模块中,实现节点坐标输入、单元节点编号、网络划分以及边界条件输入等工作;在分析主程序模块中,求解整体刚度方程;在后处理模块中,实现结果显示、数据输出等工作。本文主要针对四节点四边形单元与八节点四边形单元理论和对应的计算程序进行讲解。具体理论基础
有限元法的基本步骤:
- 几何域离散,获得标准化的单元;
- 通过能量原理(虚功原理或最小势能原理,获得单元刚度方程;
- 单元的集成(装配);
- 处理位移边界条件;
- 计算支反力;
- 计算单元的其他物理量(应力应变)。
这几步中,最核心的内容是单元研究,具体包括:
- 节点描述
- 场描述
- 单元刚度方程。
【代码截图】

【文本教程截图】

【视频教程】
本代码案例已收录至【Matlab有限元编程从入门到精通/后处理/刚度矩阵/等参单元/高斯积分/Hammer积分/非线性/静力/动力/传热/三维/二维/梁板壳/实体/平面】 Matlab有限元编程从入门到精通/后处理/刚度矩阵/等参单元/高斯积分/Hammer积分/非线性/静力/动力/传热/三维/二维/梁板壳/实体/平面_哔哩哔哩_bilibili
相关文章:

四节点/八节点四边形单元悬臂梁Matlab有限元编程 | 平面单元 | Matlab源码 | 理论文本
专栏导读 作者简介:工学博士,高级工程师,专注于工业软件算法研究本文已收录于专栏:《有限元编程从入门到精通》本专栏旨在提供 1.以案例的形式讲解各类有限元问题的程序实现,并提供所有案例完整源码;2.单元…...

机器视觉学习(一)—— 认识OpenCV、安装OpenCV
目录 一、认识OpenCV 二、通过pip工具安装OpenCV 三、PyCharm安装OpenCV 一、认识OpenCV OpenCV(Open Source Computer Vision Library,开源计算机视觉库)是一个跨平台的计算机视觉库,最初由威尔斯理工学院的Gary Bradski于199…...

web3 DePIN赛道之OORT
文章目录 什么是DePIN什么是oort背景:去中心化云计算场景团队OORT AIOORT StorageOORT Compute 参考 什么是DePIN DePIN是Decentralized Physical Infrastructure Networks的简称,中文意思就是去中心化的网络硬件基础设施,是利用区块链技术和代币奖励来调动分散在世…...
QString 与 字符编码 QTextCodec
为了理解编码,我们要先区分 文件中字符编码 和 程序运行时字符编码 的区别。 文件中字符编码 顾名思义 就是 文字保存在文件中的采用的字符编码方式,可以在IDE中看到程序运行时字符编码,是编译器读取从源文件中读取到字符串后再按要求做的一次…...
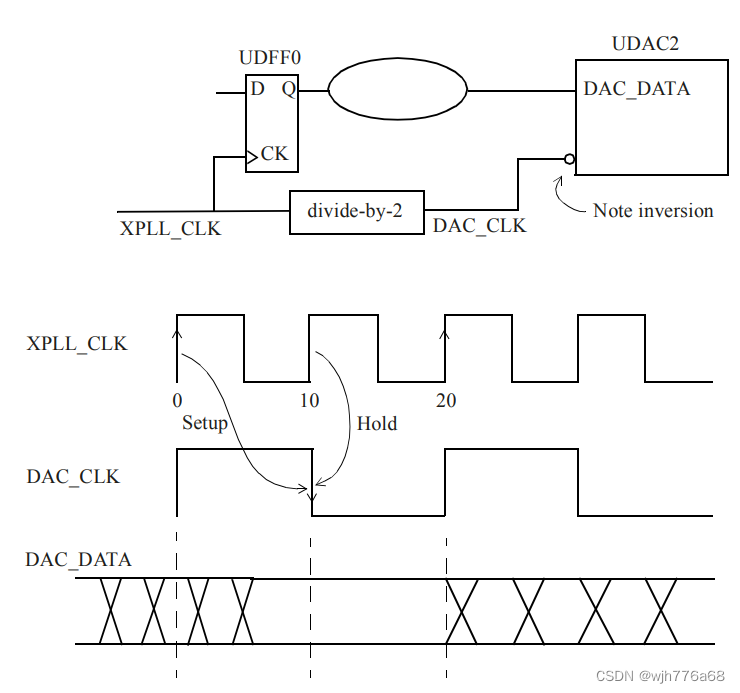
【STA】SRAM / DDR SDRAM 接口时序约束学习记录
1. SRAM接口 相比于DDR SDRAM,SRAM接口数据与控制信号共享同一时钟。在用户逻辑(这里记作DUA(Design Under Analysis))将数据写到SRAM中去的写周期中,数据和地址从DUA传送到SRAM中,并都在有效时…...

Git的基础使用
几条铁令!!!!! 切换分支前先提交本地的修改代码及时提交,提交过就不会丢遇到任何问题都不要删除文件目录,第一时间找人请教push前和merge前一定要pull保证代码为最新的,有冲突解决冲…...

贪吃蛇(C语言实现)
贪食蛇(也叫贪吃蛇)是一款经典的小游戏。 —————————————————————— 本博客实现使用C语言在Windows环境的控制台中模拟实现贪吃蛇小游戏。 实行的基本功能: • 贪吃蛇地图的绘制 • 蛇吃食物的功能(上、…...

使用 mysqldump 迁移 MySQL 表 OceanBase
使用 mysqldump 迁移 MySQL 表 OceanBase 一、什么是mysqldump二、使用mysqldump导出MySQL数据三、将数据导入到OceanBase四、注意 一、什么是mysqldump mysqldump 是 MySQL 数据库管理系统中的一个工具,用于将数据库中的数据导出为文本文件。它可以将整个数据库、…...
谷粒学院--在线教育实战项目【一】
谷粒学院--在线教育实战项目【一】 一、项目概述1.1.项目来源1.2.功能简介1.3.技术架构 二、Mybatis-Plus概述2.1.简介2.2.特性 三、Mybatis-Plus入门3.1.创建数据库3.2.创建 User 表3.3.初始化一个SpringBoot工程3.4.在Pom文件中引入SpringBoot和Mybatis-Plus相关依赖3.5.第一…...
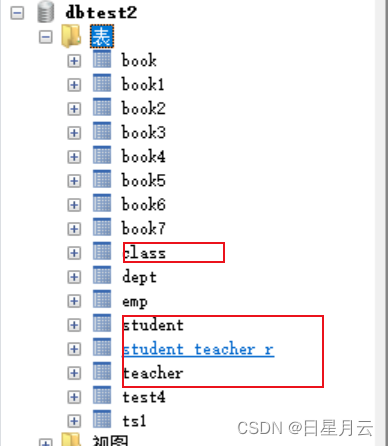
Power Design【数据库设计】
Power Design【数据库设计】 前言版权推荐Power Design【数据库设计】推荐11. PowerDesigner的使用11.1 开始界面11.2 概念数据模型11.3 物理数据模型11.4 概念模型转为物理模型11.5 物理模型转为概念模型11.6 物理模型导出SQL语句补充:sqlyog导入sql文件 最后 前言 2024-3-11…...

Spring Boot中Excel数据导入导出的高效实现
🌟 前言 欢迎来到我的技术小宇宙!🌌 这里不仅是我记录技术点滴的后花园,也是我分享学习心得和项目经验的乐园。📚 无论你是技术小白还是资深大牛,这里总有一些内容能触动你的好奇心。🔍 &#x…...
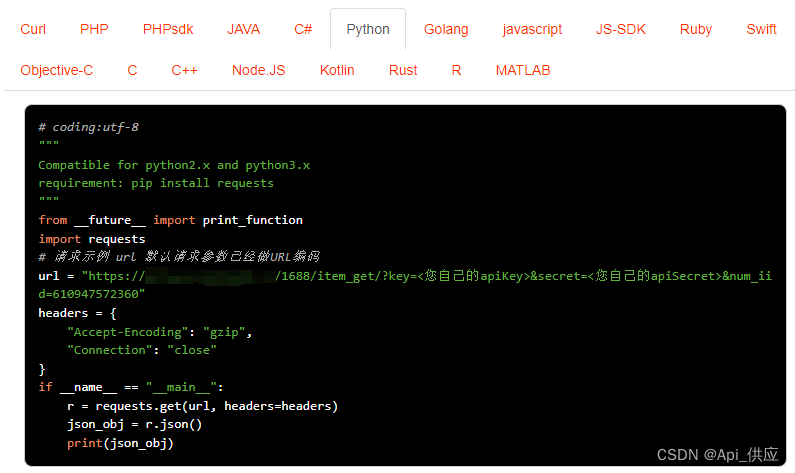
采购代购系统独立站,接口采集商品上货
采购代购系统独立站的建设与商品上货接口的采集是一个综合性的项目,涉及前端开发、后端开发、数据库设计以及API接口的对接等多个环节。以下是一个大致的步骤和考虑因素: 一、系统规划与需求分析 明确业务需求:确定代购系统的核心功能&…...
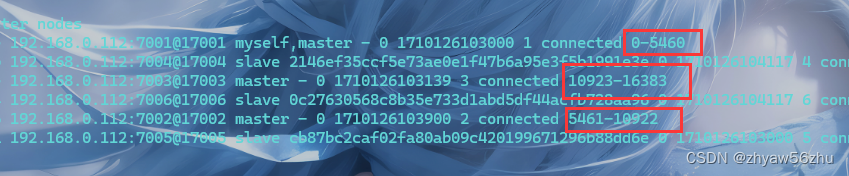
Redis精讲
redis持久化 RDB方式 Redis Database Backup file (redis数据备份文件), 也被叫做redis数据快照. 简单来说就是把内存中的所有数据记录到磁盘中. 快照文件称为RDB文件, 默认是保存在当前运行目录. [rootcentos-zyw ~]# docker exec -it redis redis-cli 127.0.0.1:6379> sav…...

ELFK 分布式日志收集系统
ELFK的组成: Elasticsearch: 它是一个分布式的搜索和分析引擎,它可以用来存储和索引大量的日志数据,并提供强大的搜索和分析功能。 (java语言开发,)logstash: 是一个用于日志收集,处理和传输的…...

excel批量数据导入时用poi将数据转化成指定实体工具类
1.实现目标 excel进行批量数据导入时,将批量数据转化成指定的实体集合用于数据操作,实现思路:使用注解将属性与表格中的标题进行同名绑定来赋值。 2.代码实现 2.1 目录截图如下 2.2 代码实现 package poi.constants;/*** description: 用…...
【软件工程导论】——软工学绪论及传统软件工程(学习笔记)
📖 前言:随着软件产业的发展,计算机应用逐步渗透到社会生活的各个角落,使各行各业都发生了很大的变化。这同时也促使人们对软件的品种、数量、功能和质量等提出了越来越高的要求。然而,软件的规模越大、越复杂…...
C语言编译成库文件的要求
keil编译成库文件 在Keil中,将C语言源文件编译成库文件通常需要进行以下步骤: 创建一个新的Keil项目,并将所需的C语言源文件添加到该项目中。 在项目设置中配置编译选项,确保生成的目标文件符合库文件的标准格式。 编译项目&…...

Python的模块应用和文件I/O
Python 解释 Python是一种高级编程语言,以其简洁、易读和易用而闻名。它是一种通用的、解释型的编程语言,适用于广泛的应用领域,包括软件开发、数据分析、人工智能等。python是一种解释型,面向对象、动态数据类型的高级程序设计…...

设计模式之依赖倒转原则
目录 1、 基本介绍 2、 应用实例 3、 依赖关系传递的三种方式 (1) 接口传递 (2) 构造方法传递 (3) setter方式传递 4、 注意事项和细节 1、 基本介绍 依赖倒转原则(Dependence Inversion Principle)是指: 高层模块不应该依赖低层模块,二者都应该依…...

Springboot启动后想要做某些事可以通过什么方法实现?
在Spring Boot应用中,如果你想在应用启动完成后执行一些特定的操作(例如缓存预热),可以实现CommandLineRunner或ApplicationRunner接口。这两个接口都提供了一个run方法,在Spring Boot应用上下文初始化完成后会被自动调…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...
