【数据结构:树与堆】向上/下调整算法和复杂度的分析、堆排序以及topk问题
文章目录
- 1.树的概念
- 1.1树的相关概念
- 1.2树的表示
- 2.二叉树
- 2.1概念
- 2.2特殊二叉树
- 2.3二叉树的存储
- 3.堆
- 3.1堆的插入(向上调整)
- 3.2堆的删除(向下调整)
- 3.3堆的创建
- 3.3.1使用向上调整
- 3.3.2使用向下调整
- 3.3.3两种建堆方式的比较
- 3.4堆排序
- 3.5TopK问题

1.树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。如下图:
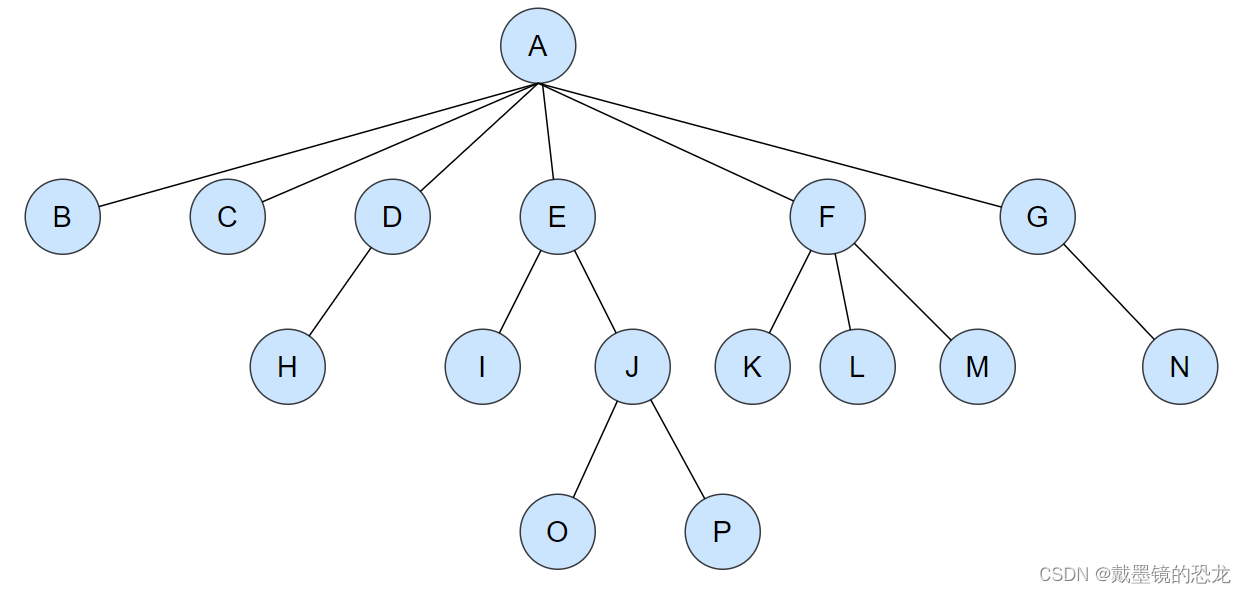
有一个特殊的结点,称为根结点,根节点没有前驱结点。例如A节点
除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。
例如:B节点又可以分成一棵树,该树只有根,没有子树。
D节点可以分为根节点和子树。D为根节点,只有一棵子树H。
因此树可以拆分为:根和子树。 每棵子树的根结点有且只有一个前驱,可以有0个或多个后继;所以,树是递归定义的。
注意:树形结构中,子树之间不能有交集,否则就不是树形结构,即:树中不能有环!。例如:
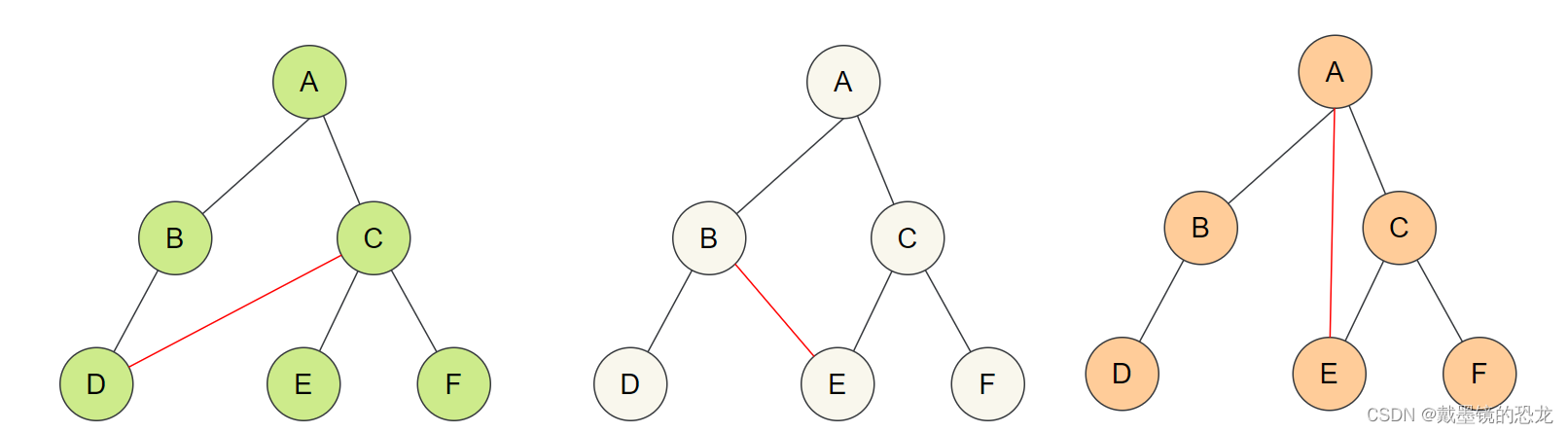

1.1树的相关概念
- 节点的度:一个
节点含有的子树的个数称为该节点的度; 如上图:A的为6 - 叶节点或终端节点:
度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点 - 分支节点或非终端节点:
度不为0的节点; 如上图:D、E、F、G…等节点为分支节点 - 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的
子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点,H是D的孩子节点 - 兄弟节点:具有
相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点 - 树的度:一棵树中,
最大的节点的度称为树的度; 如上图:树的度为6 - 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中
节点的最大层次; 如上图:树的高度为4 - 堂兄弟节点:
双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点 - 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先;P的祖先是A、E、J
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m(m>0)棵互不相交的树的集合称为森林;
1.2树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系。所以树的结构应该怎么定义呢?
//假设树的度为6
#define N 6
struct TreeNode
{int val;struct TreeNode* Child[N];
};
如果这样定义的话,不管你子树有没有孩子都开辟了空间,会比较浪费。
struct TreeNode
{int val;struct TreeNode** Child;//使用顺序表存储孩子int size;//当前个数int capacity;//容量
};
既然浪费了空间,那咱们就动态申请,有几个孩子由size决定,不够就扩容,但这种结构好像也不太好。
struct TreeNode
{int val;struct TreeNode* leftChile;//左孩子struct TreeNode* nextBrother;//右兄弟
};
左孩子右兄弟法:这种方法设计的非常巧妙,每个节点只记录它左边第一个孩子,其它孩子是第一个孩子的兄弟,由第一个孩子记录。这种方法好像看起来是最好的
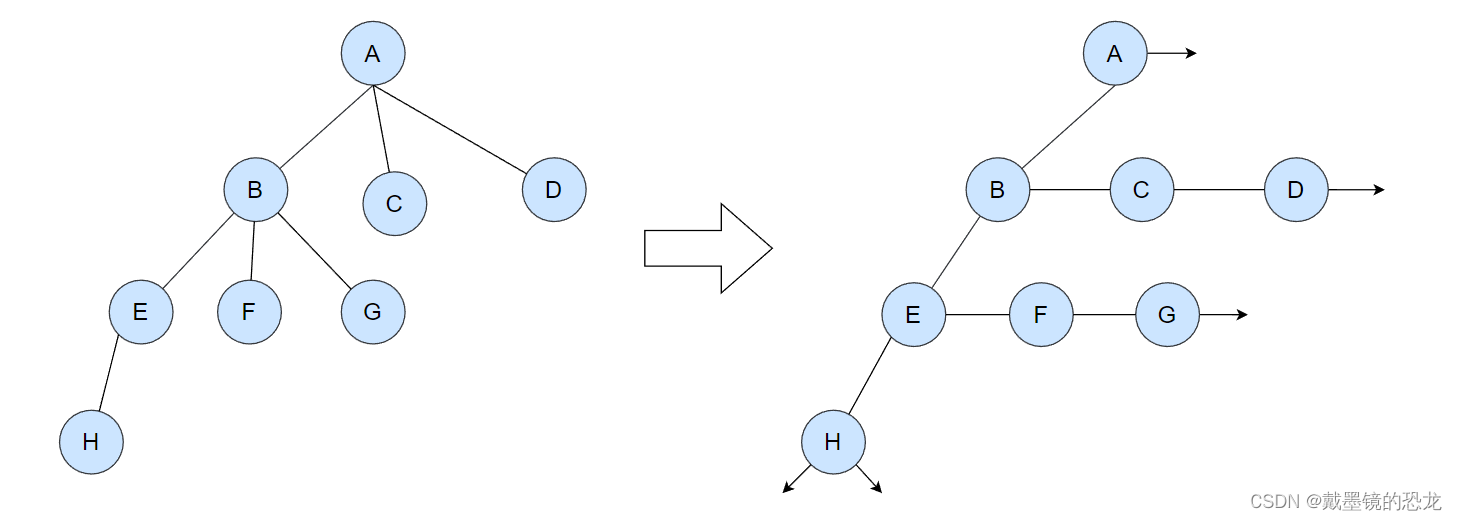
2.二叉树
2.1概念
二叉树是从树衍生出来的。
那什么叫二叉树呢?
二叉树:首先它是一棵树,其次它每个节点最多有两个分支;并且对两个分支进行区分,分别叫做左子树和右子树。如下图
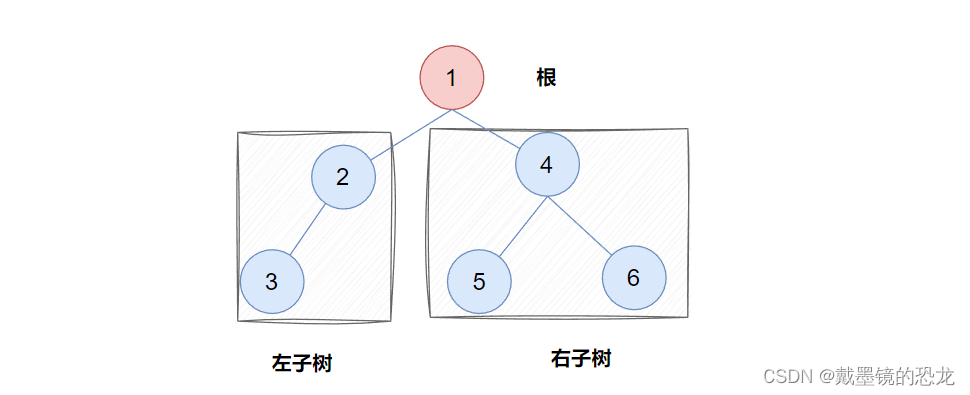
从上图可以看出:
- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:
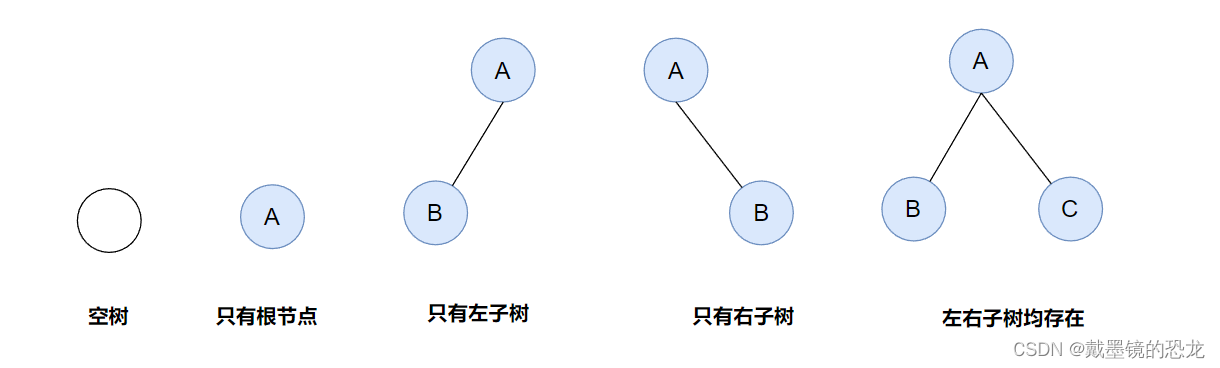
2.2特殊二叉树
- 满二叉树
满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。
满二叉树的前n-1层全是满的(度为2),叶子全在最后一层
如果一个二叉树的层数为K,且结点总数是2k-1,则这个二叉树就是满二叉树。
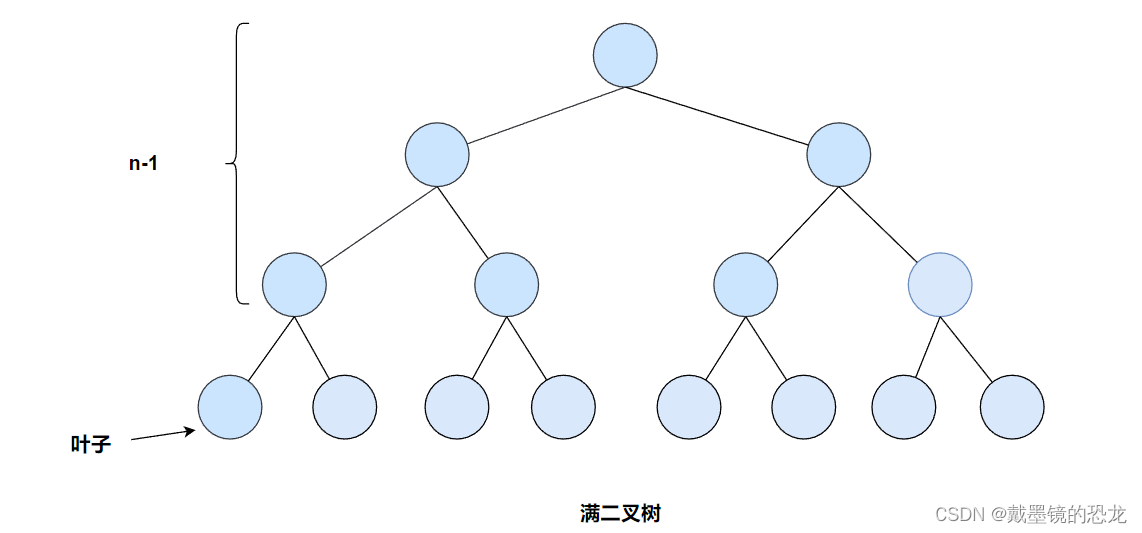
- 完全二叉树
完全二叉树跟满二叉树的区别是:完全二叉树的前n-1层也都是满的,最后一层不一定满,但是要求从左到右的节点连续,不能空。(没有左孩子就不能有右孩子)
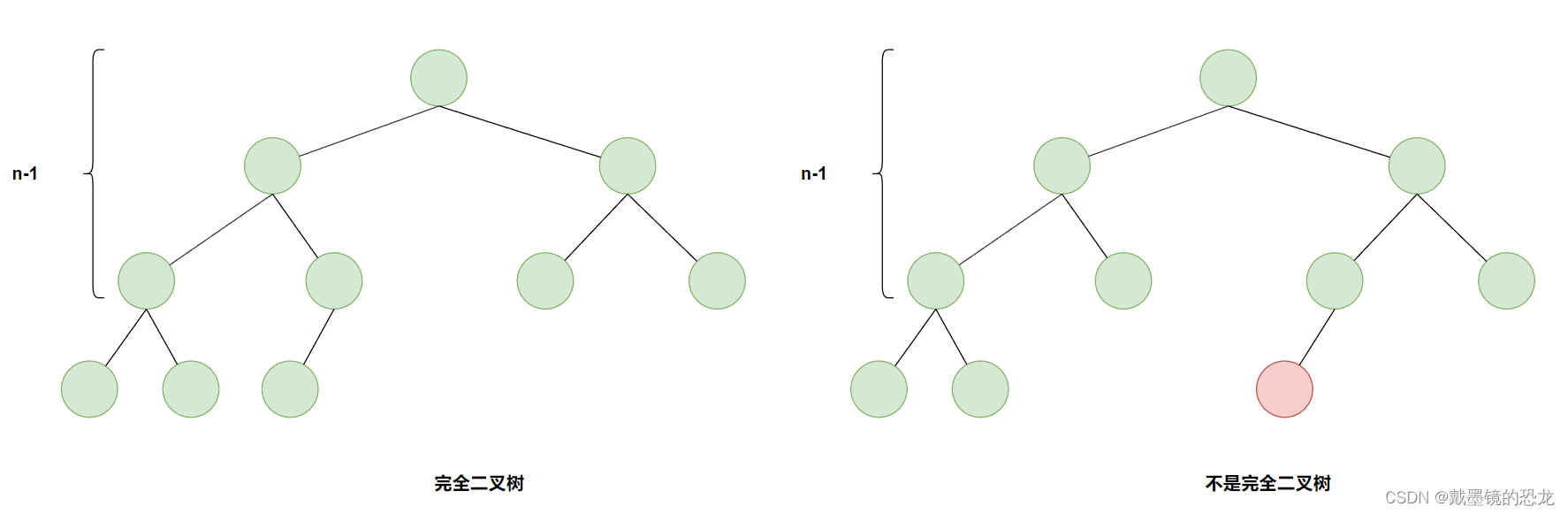
2.3二叉树的存储
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
- 顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树
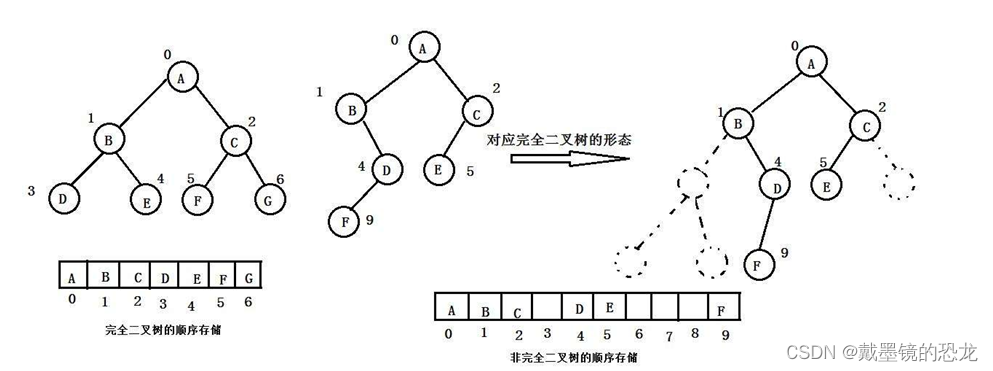
使用顺序存储存在一个规律:
-
leftChild = parent*2+1
- 例:C的左孩子的下标为2 * 2+1 = 5
-
rightChild = parent*2+2
- 例:C的右孩子的下标为2 * 2+2 = 6
-
parent = (Child - 1) / 2
- 例:F的父亲下标为(5-1)/ 2 = 2 G的父亲下标为(6-1)/ 2 = 2
-
有了这个规律我就不需要存储我的孩子或父亲在哪里,我使用下标算就可以了。
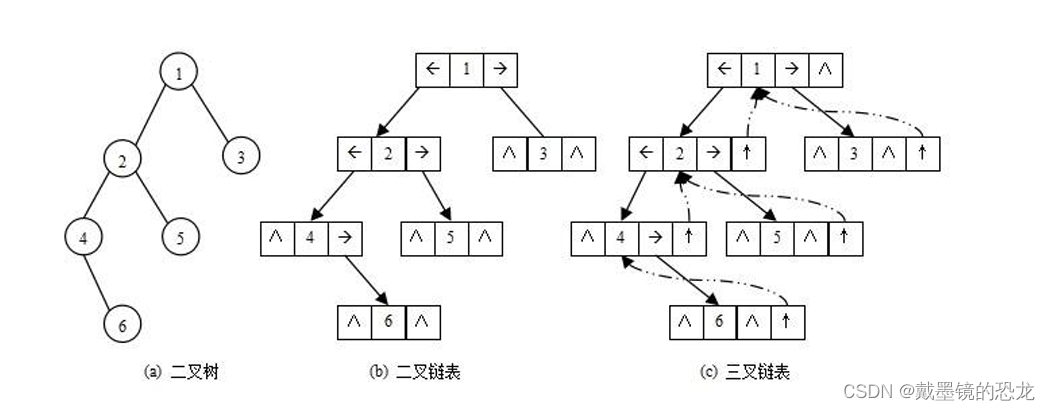
- 链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别 用来给出该结点左孩子和右孩子所在的链结点的存储地址,链式结构又分为二叉链和三叉链, 。
该结构一般用来存储非完全二叉树,不会有空间的浪费。
3.堆
- 普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。
- 完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储
堆:
- 堆是一棵完全二叉树。
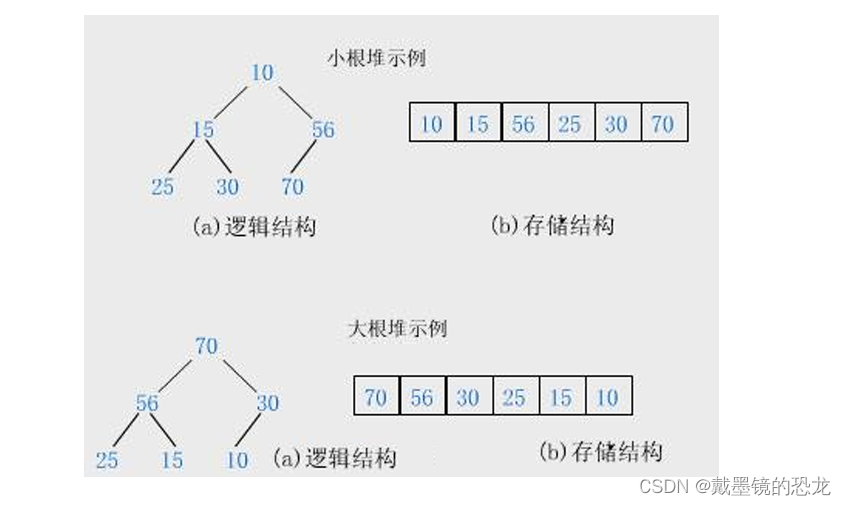
- 小堆:任何一个父亲 <= 孩子
- 大堆:任何一个父亲 >= 孩子
- 将根节点最大的堆叫做最大堆或大根堆,
根节点最小的堆叫做最小堆或小根堆
使用堆这种数据结构有什么好处呢?
TopK问题(找最值),最值就在根上。
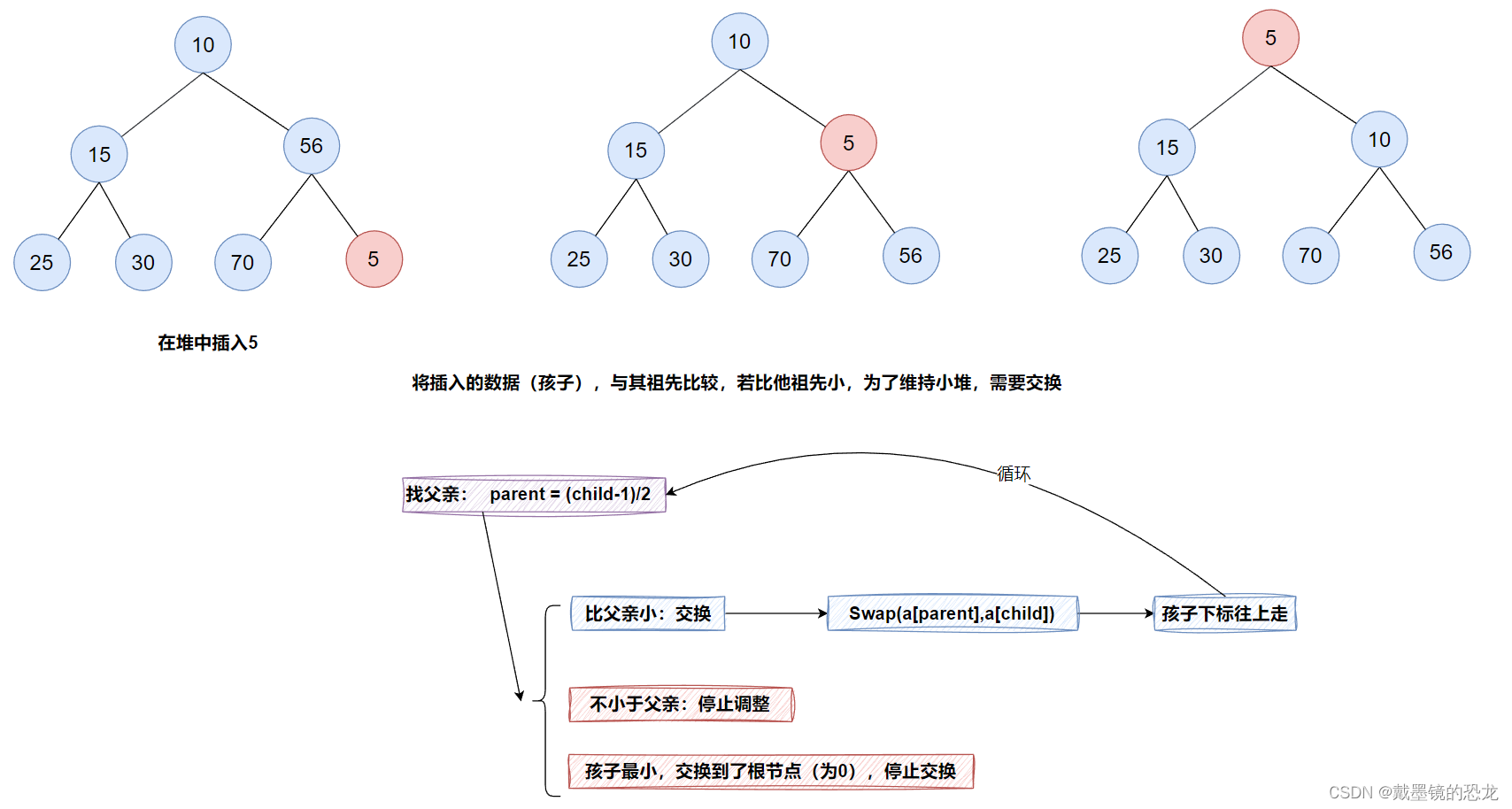
3.1堆的插入(向上调整)
假设已存在一个堆,现需向堆中插入元素5。
void Swap(HeapDataType* x, HeapDataType* y)
{HeapDataType tmp = *x;*x = *y;*y = tmp;
}void AdjustUp(HeapDataType* a, int child)
{int parent = (child - 1) / 2;//while(parent >= 0)while (child){//孩子小于父亲if (a[child] < a[parent]){//交换Swap(&a[child], &a[parent]);//改变下标child = parent;//继续找父亲parent = (child - 1) / 2;}else{break;}}
}// 堆的插入
void HeapPush(Heap* php, HeapDataType x)
{assert(php);//扩容if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HeapDataType* tmp = (HeapDataType*)realloc(php->a, sizeof(HeapDataType)*newcapacity);if (tmp == NULL){perror("realloc");return;}php->a = tmp;php->capacity = newcapacity;}//将数据先插入到堆中php->a[php->size] = x;php->size++;//插入后向上调整,使其仍然是堆//开始调整的位置为数组末尾位置:size-1AdjustUp(php->a, php->size - 1);
}
思考:如何让一个数组变成堆?
将数组的值插入堆中即可
int main()
{Heap* heap = HeapCreate();int arr[] = { 1,4,7,3,9,10 };for (int i = 0; i < sizeof(arr)/sizeof(int); i++){HeapPush(heap, arr[i]);}HeapDestroy(heap);return 0;
}
3.2堆的删除(向下调整)
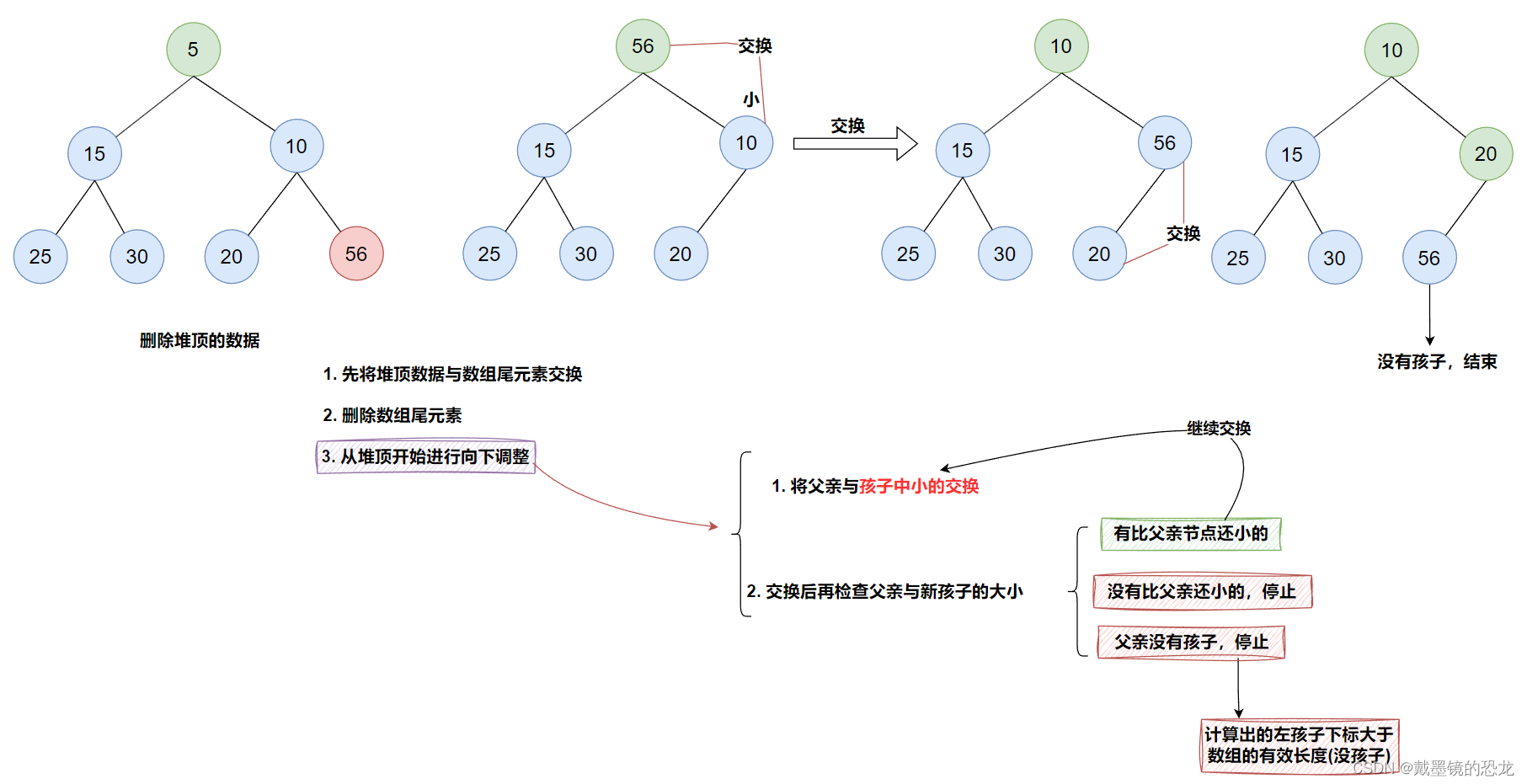
void AdjustDown(HeapDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n)//有左孩子就继续{//找小的孩子//若右孩子存在 且 右孩子小于左孩子,右孩子是小孩子if (child+1 < n && a[child+1] < a[child]){child++;}//小孩子小于父亲,交换if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}// 堆的删除
void HeapPop(Heap* php)
{assert(php);assert(php->size);Swap(&php->a[0], &php->a[php->size - 1]);//交换php->size--;//删除数组尾位置AdjustDown(php->a, php->size, 0);
}
3.3堆的创建
下面我们给出一个数组,这个数组逻辑上可以看做一颗完全二叉树,但是还不是一个堆,现在我们通过算法,把它构建成一个堆。根节点左右子树不是堆,我们怎么调整呢?
3.3.1使用向上调整
从数组的第二个元素开始,使其按照小堆/大堆的规则调整成堆
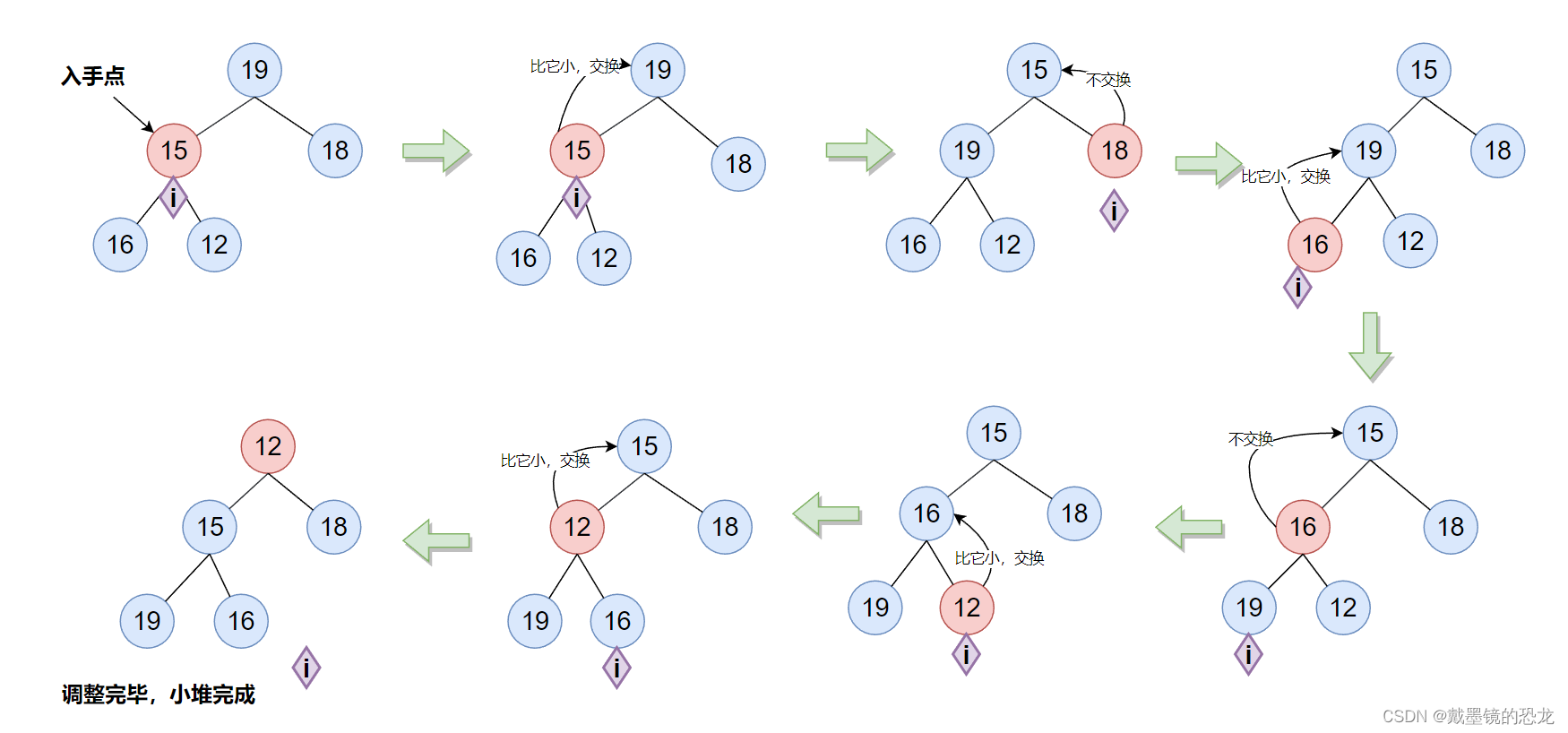
void HeapCreat(Heap* php, HeapDataType* a, int n)
{assert(php);php->a = (HeapDataType*)malloc(sizeof(HeapDataType) * n);//申请和数组同样大的空间if (php->a == NULL){perror("malloc fail");return;}memcpy(php->a, a, sizeof(HeapDataType) * n);//将数组中的元素拷贝进堆php->size = n;php->capacity = n;//向上调整,使其成堆for (int i = 1; i < n; i++){AdjustUp(php->a, i);}
}
3.3.2使用向下调整
用向下调整法,我们从倒数的第一个非叶子节点的子树开始调整,一直调整到根节点的树,就可以调整成堆。
其实本质上就是:从下往上,将根的每个子树调整成堆
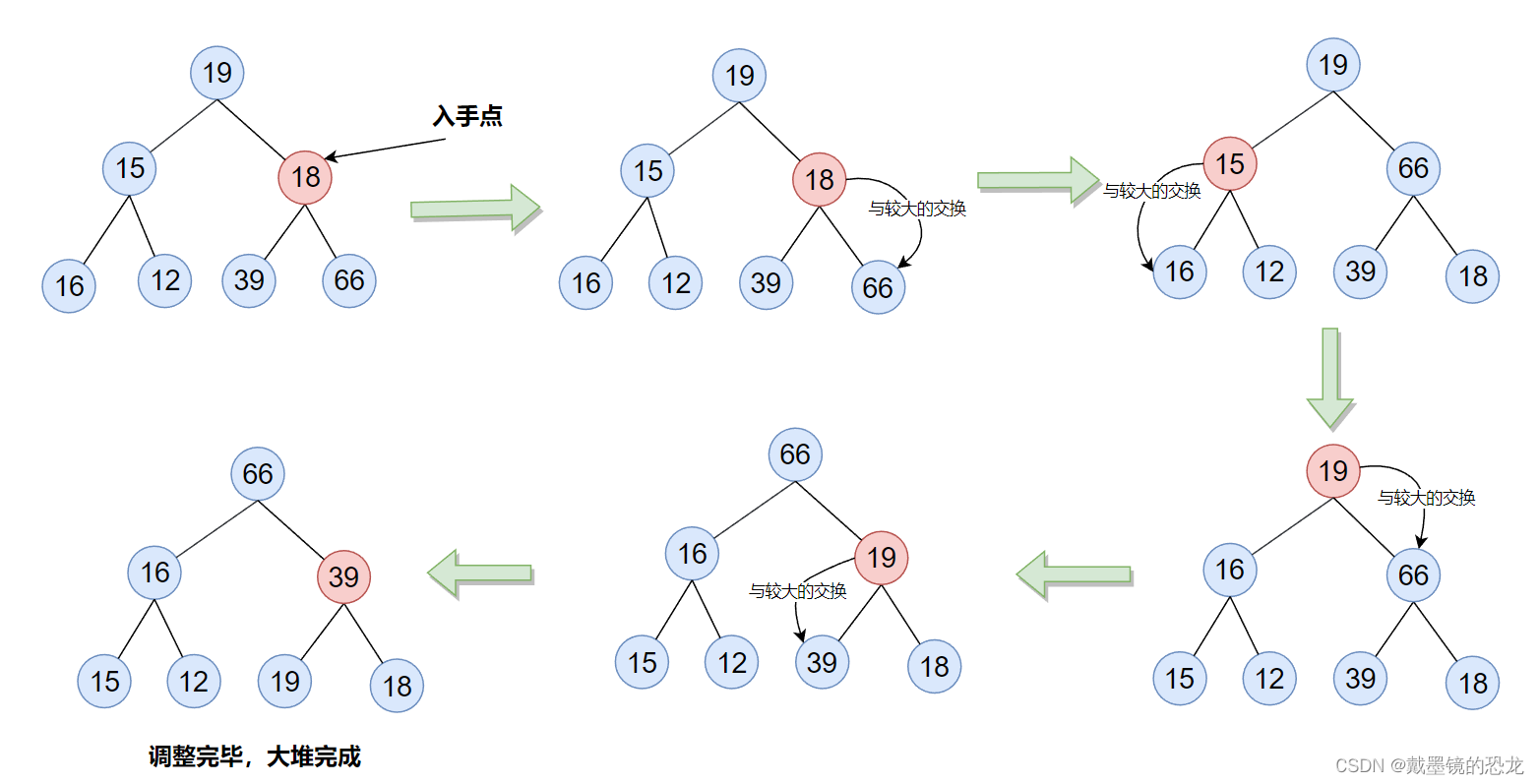
由于最后一个元素的下标为n-1,所以它的父亲应该是:(其下标-1)/2,也就是(n-1-1)/2。
void HeapCreat(Heap* php, HeapDataType* a, int n)
{assert(php);php->a = (HeapDataType*)malloc(sizeof(HeapDataType) * n);//申请和数组同样大的空间if (php->a == NULL){perror("malloc fail");return;}memcpy(php->a, a, sizeof(HeapDataType) * n);//将数组中的元素拷贝进堆php->size = n;php->capacity = n;//向下调整,使其成堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(php->a, n, i);}
}
3.3.3两种建堆方式的比较
- 树的高度与节点个数的关系
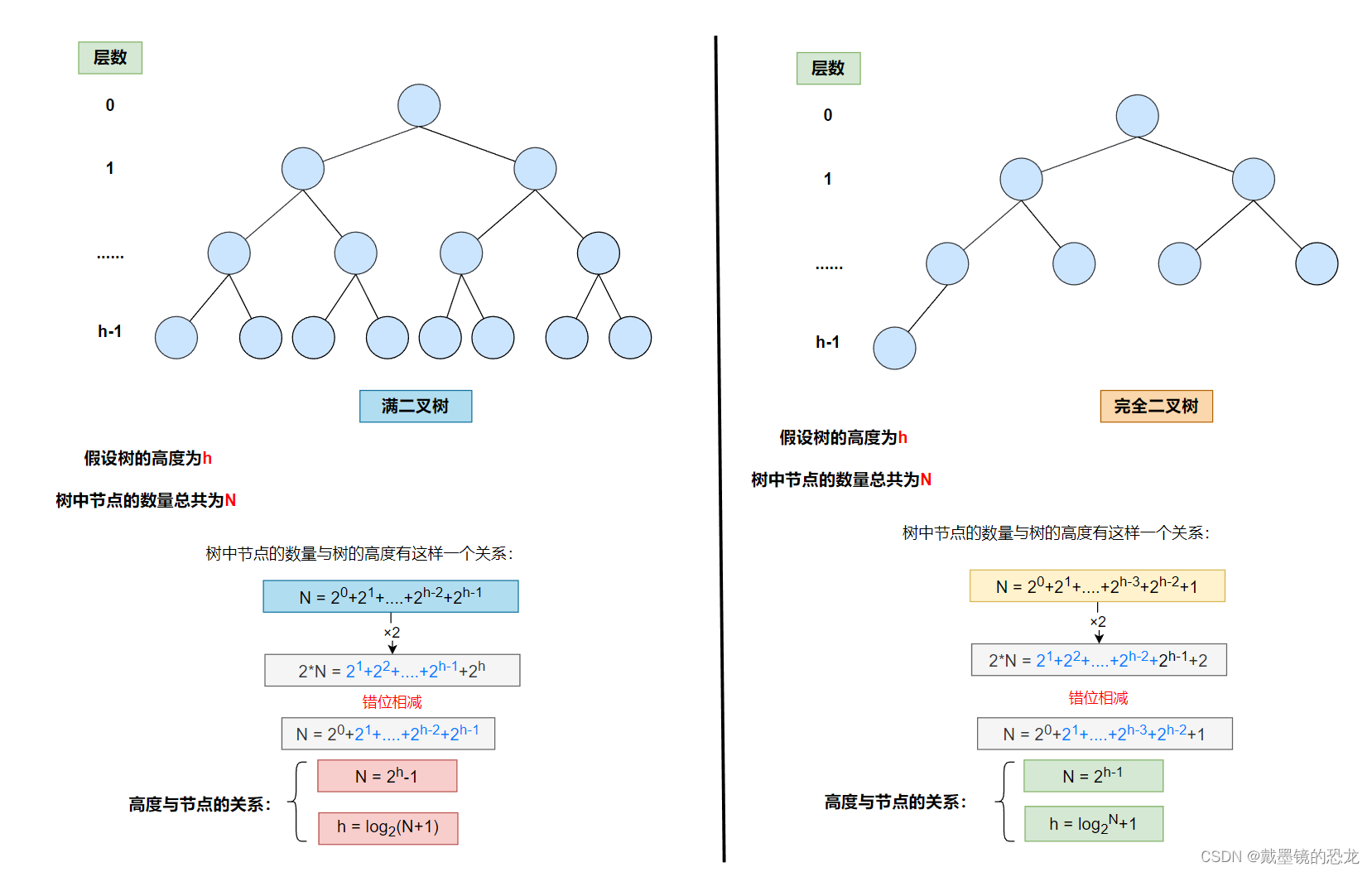
- 向上调整法建堆时间复杂度的分析
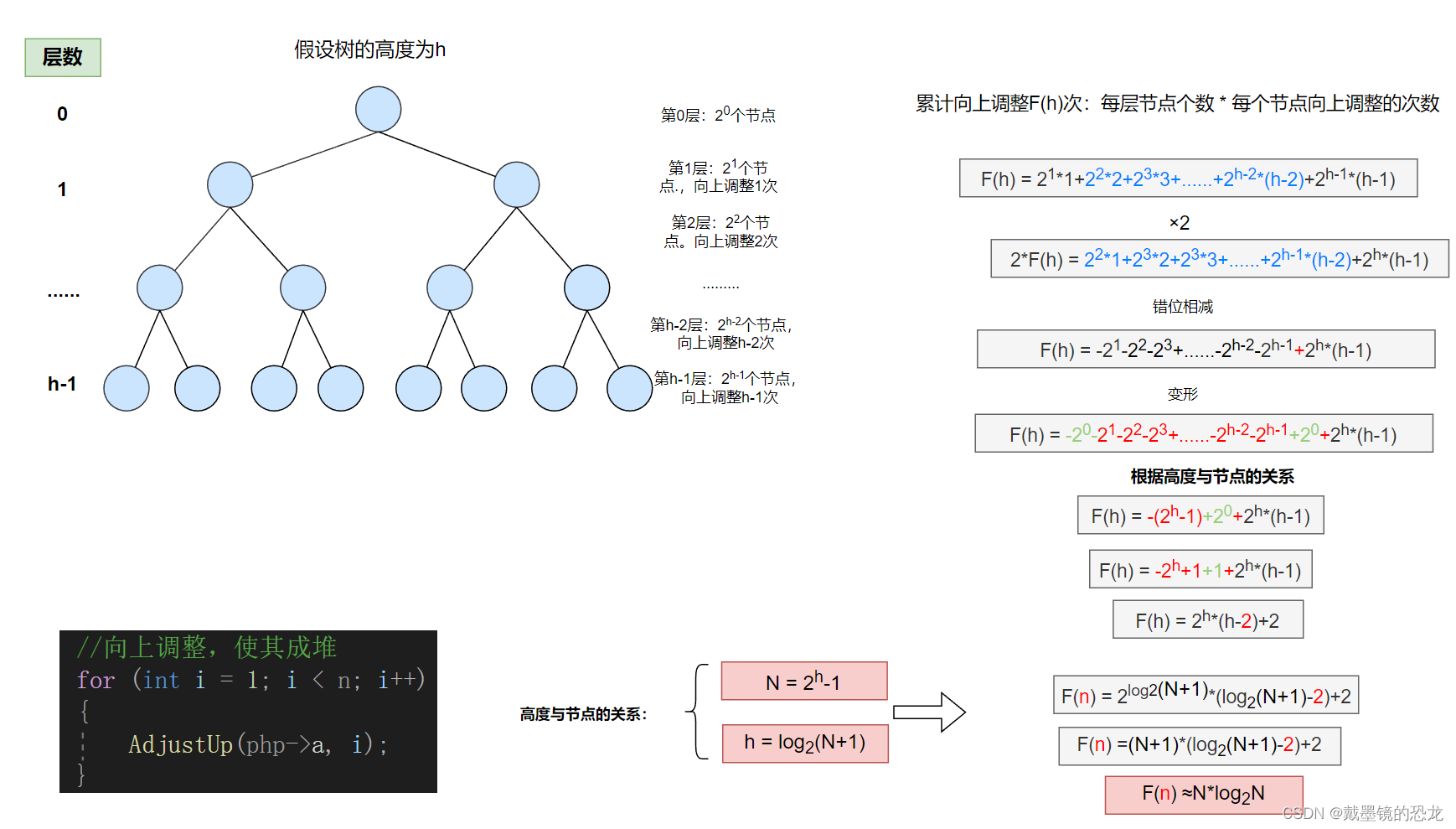
因此,向上调整建堆的时间复杂度为:O(N*log2N)
- 向下调整法建堆时间复杂度的分析
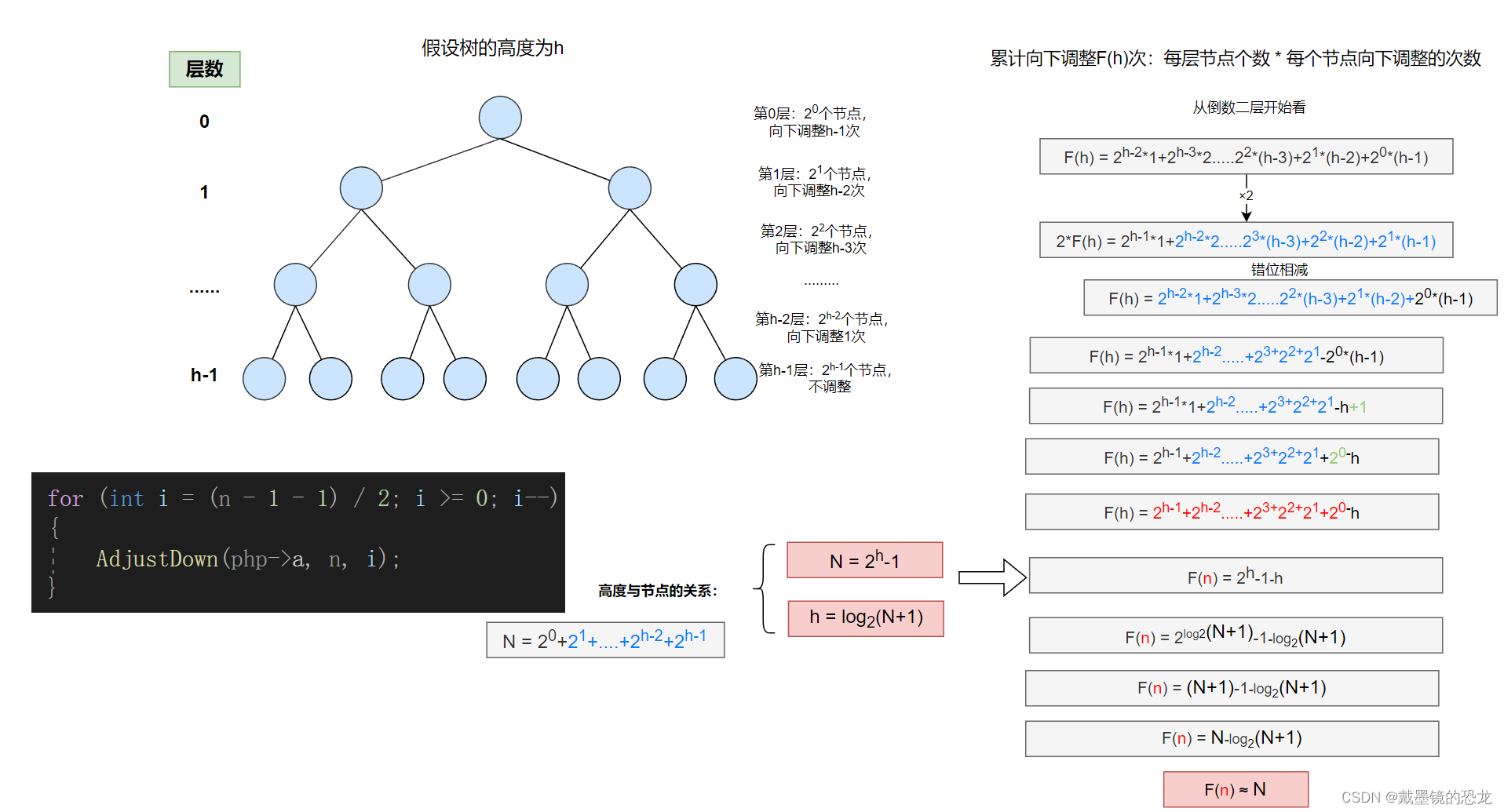
因此,向下调整建堆的时间复杂度为:O(N)
O(N*log2N) 与O(N)看来两种方法的效率差别还是挺大的。为什么差别这么大呢?

3.4堆排序
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
-
建堆
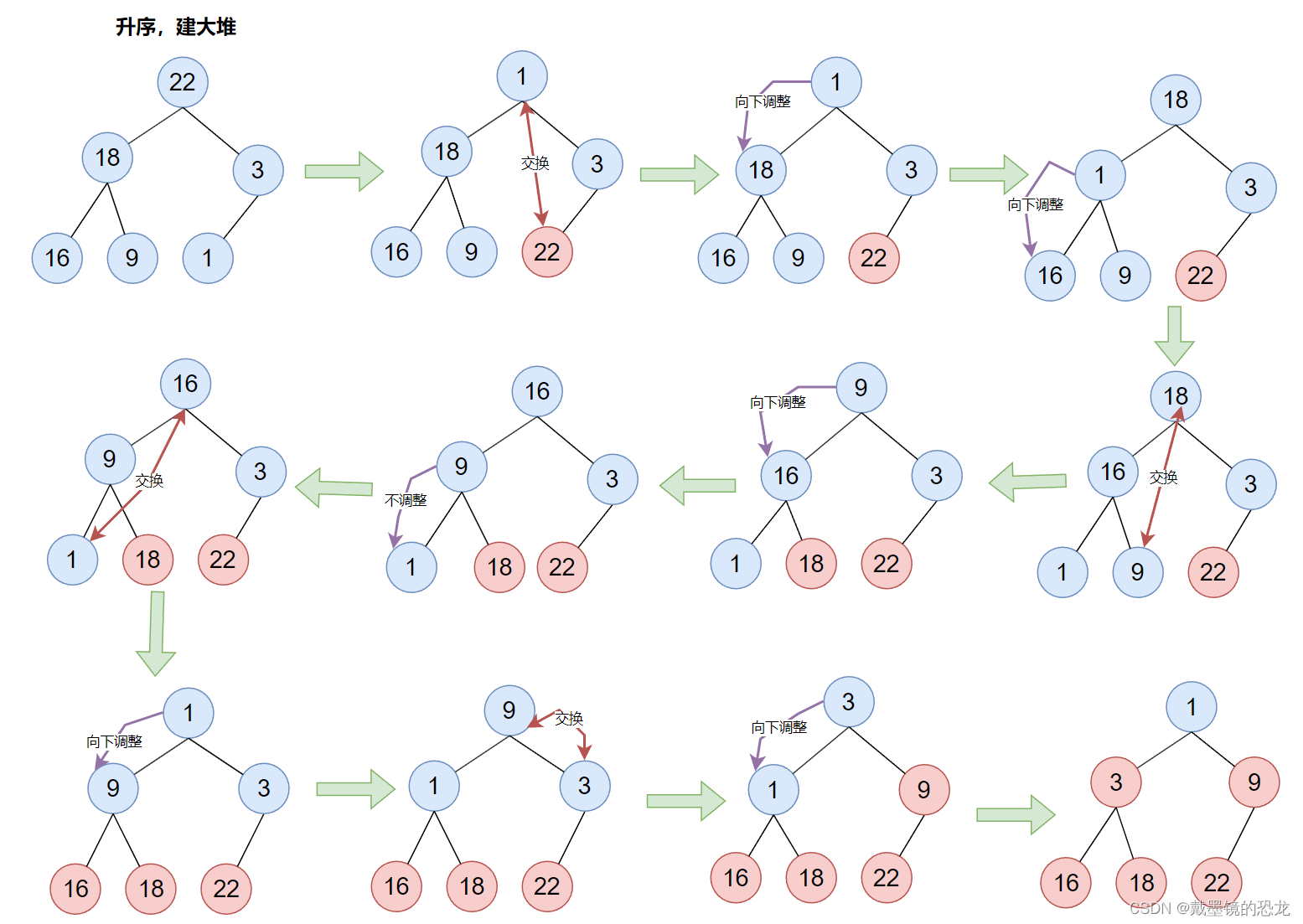
升序:建大堆
降序:建小堆 -
利用堆删除思想来进行排序
首位交换
最后一个值不看做堆里面的,向下调整选出次大的数据
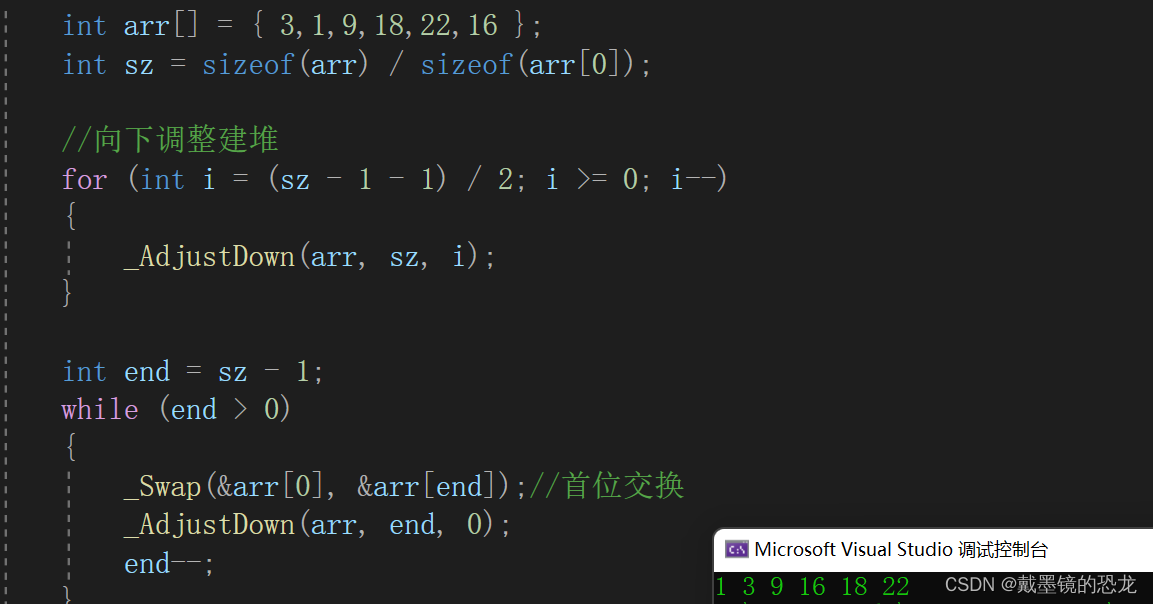
#include<stdio.h>
void _Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}void _AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){//右孩子存在,且大于左孩子if (child + 1 < n && a[child + 1] > a[child]){child++;}//孩子大于父亲,交换if (a[child] > a[parent]){_Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;//孩子不大于父亲,调整结束}}
}int main()
{int arr[] = { 3,1,9,18,22,16 };int sz = sizeof(arr) / sizeof(arr[0]);//向下调整建堆for (int i = (sz - 1 - 1) / 2; i >= 0; i--){_AdjustDown(arr, sz, i);}int end = sz - 1;while (end > 0){_Swap(&arr[0], &arr[end]);//首位交换_AdjustDown(arr, end, 0);end--;}for (int i = 0; i < sz; i++){printf("%d ", arr[i]);}return 0;
}
3.5TopK问题
TOP-K问题:即求数据中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
- 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆 - 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
- 将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
void TopK(int k)
{FILE* fp = fopen("data.txt", "r");if (fp == NULL){return;}int* heap = (int*)malloc(sizeof(int) * k);if (heap == NULL){perror("malloc fail");return;}//先读取k个数据for (int i = 0; i < k; i++){fscanf(fp, "%d", &heap[i]);}//根据k个数据建小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){_AdjustDown(heap, k, i);}int num = 0;while (fscanf(fp, "%d", &num) != EOF){//读取堆顶数据,比它大就替换它,进堆if (num > heap[0]){heap[0] = num;_AdjustDown(heap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", heap[i]);}fclose(fp);
}
相关文章:

【数据结构:树与堆】向上/下调整算法和复杂度的分析、堆排序以及topk问题
文章目录 1.树的概念1.1树的相关概念1.2树的表示 2.二叉树2.1概念2.2特殊二叉树2.3二叉树的存储 3.堆3.1堆的插入(向上调整)3.2堆的删除(向下调整)3.3堆的创建3.3.1使用向上调整3.3.2使用向下调整3.3.3两种建堆方式的比较 3.4堆排…...

vue3+element-plus el-input 自动获取焦点
虽然element有提供input的autofocus属性,但是当我们第二次进入页面就会发现autofocus已经不再生效,需要通过onMounted去触发input的focus解决这个问题。 1.先给el-input绑定一个ref:<el-input ref"inputRef" v-model"inp…...
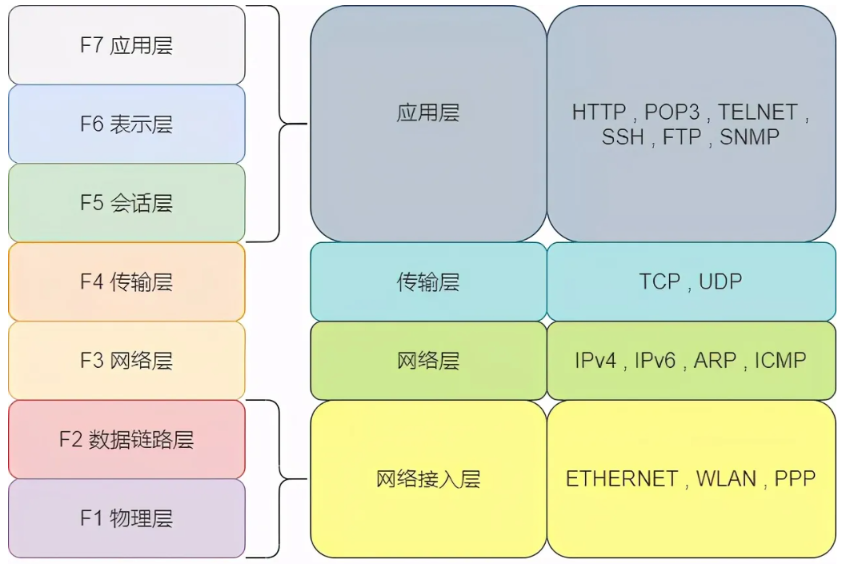
简单了解TCP/IP四层模型
什么是计算机网络? 计算机网络我们可以理解为一个巨大的城市地图,我们想从A地前往B地,其中要走的路、要避开的问题都交给计算机网络解决,直到我们可以正常的到达目的地,那么我们会把其中的过程抽象成一个网络模型&…...
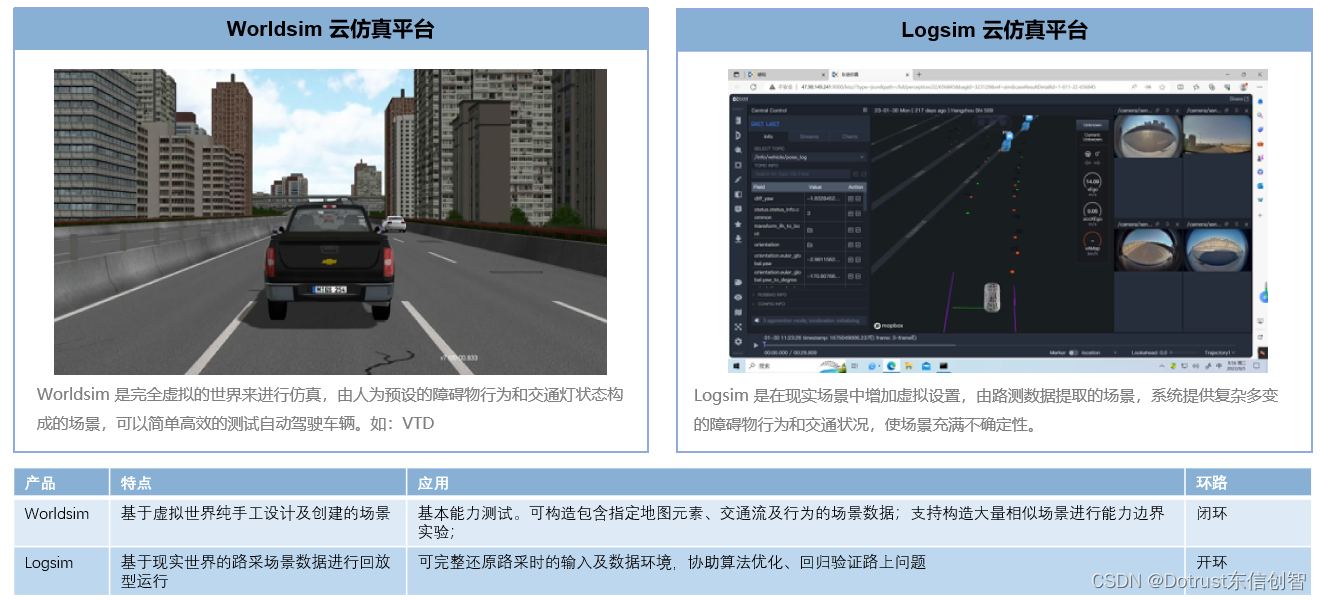
大模型时代下的自动驾驶研发测试工具链-SimCycle
前言: 最近OpenAI公司的新产品Sora的发布,正式掀起了AI在视频创作相关行业的革新浪潮,AI不再仅限于文本、语音和图像,而直接可以完成视频的生成,这是AI发展历程中的又一座重要的里程碑。AI正在不断席卷着过去与我们息…...

人工智能迷惑行为大赏
近年来,随着人工智能技术的不断发展和应用,我们在日常生活中越来越多地接触到各种智能设备和程序。然而,随之而来的是一些令人瞠目结舌的人工智能迷惑行为,让人们对这一新兴技术产生了更多的好奇和思考。 在人工智能迷惑行为大赏…...

ZJUBCA研报分享 | 《BTC/USDT周内效应研究》
ZJUBCA研报分享 引言 2023 年 11 月 — 2024 年初,浙大链协顺利举办为期 6 周的浙大链协加密创投训练营 (ZJUBCA Community Crypto VC Course)。在本次训练营中,我们组织了投研比赛,鼓励学员分析感兴趣的 Web3 前沿话题…...
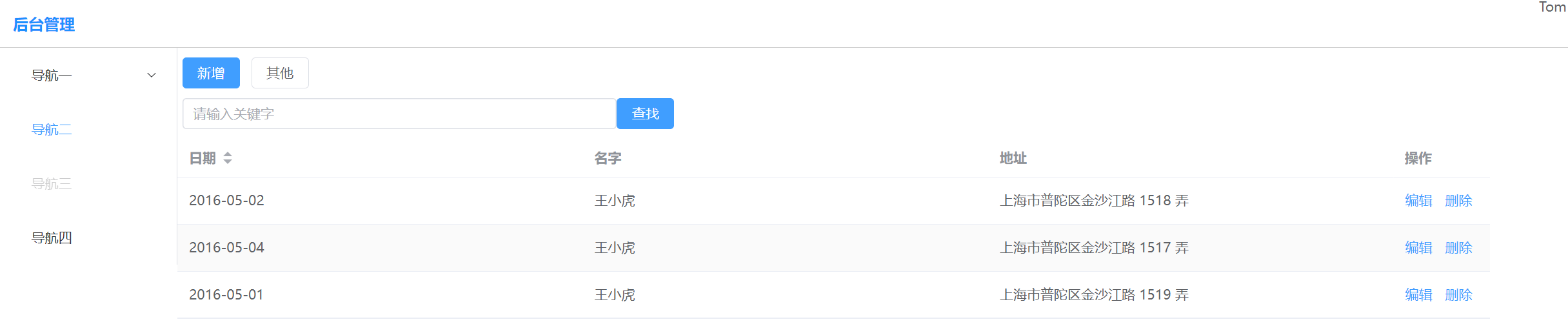
SSM整合项目(使用Vue3 + Element-Plus创建项目基础页面)
1.配置Vue启动端口 1.修改vue.config.js const {defineConfig} require(vue/cli-service) module.exports defineConfig({transpileDependencies: true }) module.exports {devServer: {port: 9999 //启动端口} }2.启动 2.安装Element Plus 命令行输入 npm install eleme…...
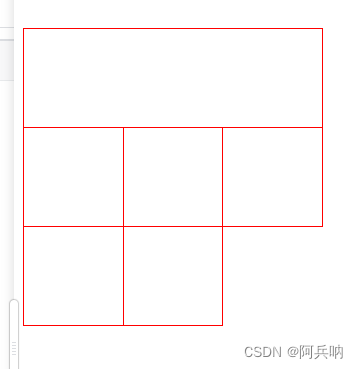
css相邻元素边框重合问题,解决方案
1、如下图所示,在给元素设置边框后,相邻元素会出现重合的问题 2、解决方案 给每个元素设置margin-top以及margin-left为负的边框 <div style"width: 300px;display: flex;flex-wrap: wrap;margin-top: 50px;"><div style"border…...
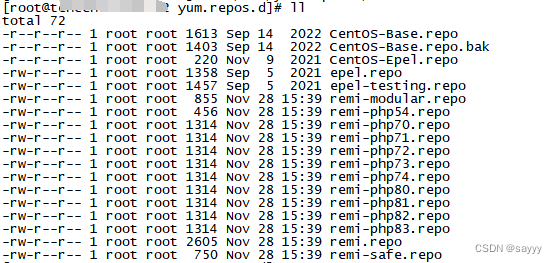
CentOS7 利用remi yum源安装php8.1
目录 前言remi yum源remi yum源 支持的操作系统remi yum源 支持的php版本 安装epel源安装remi源安装 php8.1查看php版本查看php-fpm服务启动php-fpm服务查看php-fpm服务运行状态查看php-fpm服务占用的端口查看 php8.1 相关的应用 前言 CentOS Linux release 7.9.2009 (Core) …...

深入探索Java设计模式:责任链模式解析与实践
目录 一、责任链模式的基础知识1. 模式结构2. 模式示例 二、责任链模式的实际应用1. 请求处理链2. 日志记录器 三、责任链模式的重要性和使用场景结语 欢迎阅读本篇博客,我们将深入探讨Java设计模式中的责任链模式,帮助初学者、初中级程序员和在校大学生…...

如何在项目中应用“API签名认证”
❤ 作者主页:李奕赫揍小邰的博客 ❀ 个人介绍:大家好,我是李奕赫!( ̄▽ ̄)~* 🍊 记得点赞、收藏、评论⭐️⭐️⭐️ 📣 认真学习!!!🎉🎉 文章目录 为什么需要AP…...

【AIGC+VisionPro】空间视频生意的创业者
1. 产品概述 -一款基于人工智能的2D到3D视频/图像转换工具,可将普通的2D视频/图像转换为令人惊艳的3D视觉体验。 - 它支持在PC上进行转换,并输出适用于Meta Quest、Apple Vision Pro等XR设备的3D格式。 2. 产品功能 - 利用尖端的3D AI系统,可将任何视频(Youtube、电影、游戏、…...
word转PDF的方法 简介快速
在现代办公环境中,文档格式转换已成为一项常见且重要的任务。其中,将Word文档转换为PDF格式的需求尤为突出,将Word文档转换为PDF格式具有多方面的优势和应用场景。无论是为了提高文档的可读性和稳定性、保障文档的安全性和保护机制、还是为了…...

【开源】SpringBoot框架开发图书管理系统
目录 一、 系统介绍二、 功能模块2.1 登录注册模块2.1 图书馆模块2.2 图书类型模块2.3 图书模块2.4 图书借阅模块2.5 公告模块 三、 源码解析3.1 图书馆模块设计3.2 图书类型模块设计3.3 图书模块设计3.4 图书借阅模块设计3.5 公告模块设计 四、 免责说明 一、 系统介绍 图书管…...

Java 继承与多态
一、继承 在Java中,继承是一种重要的面向对象编程概念,它允许一个类(称为子类或派生类)继承另一个类(称为父类或基类)的属性和方法。这意味着子类可以使用父类的成员变量和方法,并且可以添加自…...

C语言——递归题
对于递归问题,我们一定要想清楚递归的结束条件,每个递归的结束条件,就是思考这个问题的起始点。 题目1: 思路:当k1时,任何数的1次方都是原数,此时返回n,这就是递归的结束条件&#…...
构建空间场景轻应用,Mapmost Alpha来啦【文末赠书(10本)--第一期】
文章目录: 一、Mapmost Alpha 介绍二、Mapmost Alpha应对数字孪生业务痛点解决之道2.1 Mapmost Alpha 提供海量城市底板2.2 Mapmost Alpha 提供便捷的配置管理工具2.3 Mapmost Alpha 提供一键式部署发布和分享 三、沉浸式体验Mapmost Alpha3.1 创建应用3.2 新手指导…...
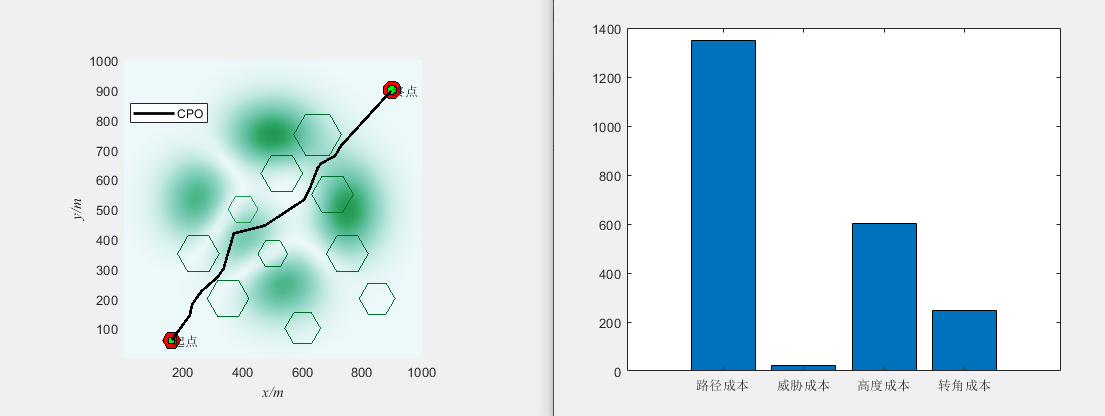
基于冠豪猪优化算法(Crested Porcupine Optimizer,CPO)的无人机三维路径规划(MATLAB)
一、无人机路径规划模型介绍 无人机三维路径规划是指在三维空间中为无人机规划一条合理的飞行路径,使其能够安全、高效地完成任务。路径规划是无人机自主飞行的关键技术之一,它可以通过算法和模型来确定无人机的航迹,以避开障碍物、优化飞行…...

html2canvas+jsPDF实现前端导出pdf
html2canvasjsPDF实现前端导出pdf 安装插件包 npm install jspdf npm install html2canvas引入插件 import html2canvas from html2canvas; import jsPDF from jspdf;生成pdf const perCanvas document.createElement(canvas);perCanvas.style.backgroundColor #fffconst …...

Paimon新版本核心特性和生产实践解读
最近Apche Paimon发布了最新版本0.7.0,在这个版本中,Paimon对一些新特性进行了增强。 Paimon在数据湖领域发展迅速,未来会在整个数据开发领域占有很重要的地位,今天我们来盘点一下当前能力的特点以及在生产环境中的使用情况。 Loo…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
