AcWing 4956. 冶炼金属
对于这个题,V越大,除出来的数就越小,V越小,除出来的数就越大,当我们找一个最大和最小值的时候,就可以通过这个性质进行二分来求解。
可以通过求满足 [ A V ] [\frac{A}{V}] [VA] 小于等于 B B B的最小的 V V V来求最小值,通过满足 [ A V ] [\frac{A}{V}] [VA] 小于等于 B − 1 B-1 B−1的 V V V最小的值来求最大值(这里是根据下取整函数的性质来决定的,取整函数的函数图像是一段段的横线,可以观察得B的V的最大值就是B-1的V的最小值)。
代码1:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;int get(int a, int b) {//二分函数//b最小取1,但是下面调用函数时有b-1,所以b有可能取到0,那么r就要取到比1e9大//则定义r为1e9+1int l = 1, r = 1e9 + 1;while (l < r) {int mid = l + r >> 1;if (a / mid <= b)r = mid;else l = mid + 1;}return r;
}int main() {int n; cin >> n;//最小一定是1,最大只能取1e9,大于1e9时B会得到0,不满足题目条件int minV = 1, maxV = 1e9;while (n--) {int a, b; cin >> a >> b;minV = max(minV, get(a,b));maxV = min(maxV, get(a, b - 1) - 1);}cout << minV << " " << maxV;return 0;
}
另一种二分法:
当我们要求V的最小值的时候,先浮现出一个数轴
|----------------------|----------------------|
L mid R
因为这里是找数,所以不是之前的那些需要满足条件,这里只需要看大小关系。
如果 [ A m i d ] [\frac{A}{mid}] [midA]大于B,就说明mid取小了,所以就要往右边找,也就是从mid +1 ~ R找,如果小于B,那就要从L ~ mid找。
对于求最大值也是同理。
另一种代码:非常模板风味的二分代码:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e4 + 10;int n;
int a[N], b[N];bool check1(int mid) { //check1求最小值用for (int i = 0; i < n; i++) {if (a[i] / mid > b[i])return false; }return true;
}bool check2(int mid) { //check2求最大值用for (int i = 0; i < n; i++) {if (a[i] / mid < b[i])return false;}return true;
}int main() {cin >> n;for (int i = 0; i < n; i++) cin >> a[i] >> b[i];//求最小值int l = 1, r = 1e9;while (l < r) {int mid = l + r >> 1;if (check1(mid))r = mid;else l = mid + 1;}cout << r << " ";//求最大值l = 1, r = 1e9;while (l < r) {int mid = l + r + 1 >> 1;if (check2(mid)) l = mid;else r = mid - 1;}cout << r << endl;return 0;
}
由于是复习二分,故不记录数学做法
相关文章:

AcWing 4956. 冶炼金属
对于这个题,V越大,除出来的数就越小,V越小,除出来的数就越大,当我们找一个最大和最小值的时候,就可以通过这个性质进行二分来求解。 可以通过求满足 [ A V ] [\frac{A}{V}] [VA] 小于等于 B B B的最小的…...

记一次面试经历
这段时间正好是金三银四的黄金时间段,正好这段时间也有很多企业有hc在招人,本文主要就是来聊聊我这段时间的面试经历吧。目前我是从北京投上海的岗位,现在有两家保底的offer。 简历投递 简历这块是基础也是必要的门槛,有没有面试…...
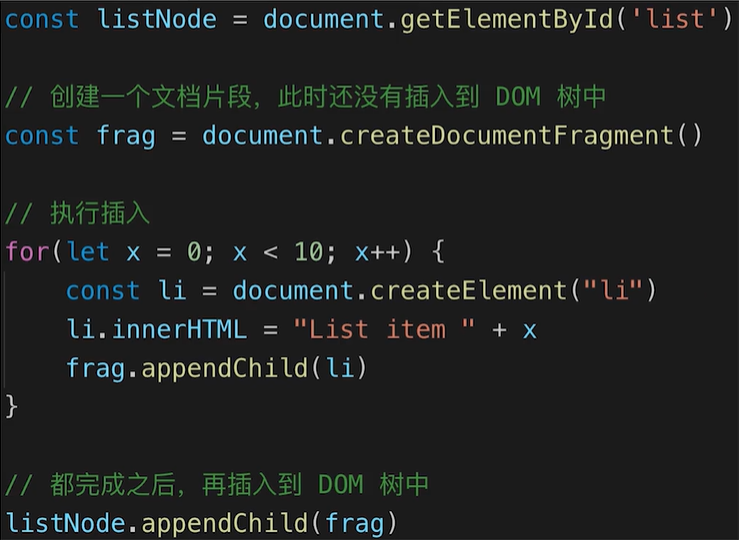
js【详解】DOM
文档对象模型(Document Object Model,简称DOM) DOM 是哪种数据结构 ? DOM 的本质是浏览器通过HTML代码解析出来的一棵 树。 操作 DOM 常用的 API 有哪些 ? 获取 DOM 节点 //方式 1:通过【id】获取…...
《互联网的世界》第六讲-去中心化和安全
互联网构建于开放互联的中立原则之上,公平接入,数据互联互通,流量被无差别对待,这意味着互联网本质上是匿名,去中心的,这与我们的现实世界完全不同。 但互联网上的主流业务却是 c/s 产销模式,试…...
nginx代理参数proxy_pass
proxy_pass参数用于配置反向代理,指定客户端请求被转发到后端服务器,后端地址可以是域名、ip端口URI 代理后端报错提示本地找不到CSS文件、JavaScript文件或图片 例如: nginx :10.1.74.109 后端服务:http://10.1.74.…...

_note_01
1.什么是跨平台 跨平台是指一个应用程序或一个编程语言,可以在不同的操作系统或平台上运行,而不需要对代码进行修改或重新编译。 跨平台应用程序或编程语言的设计和实现可以使开发者减少对特定平台的依赖,从而降低维护和开发的成本。同时&am…...

聊聊python中面向对象编程思想
面向对象编程思想 1、什么是面向过程 传统的面向过程的编程思想总结起来就八个字——自顶向下,逐步细化! → 将要实现的功能描述为一个从开始到结束按部就班的连续的“步骤” → 依次逐步完成这些步骤,如果某一个步骤的难度较大ÿ…...
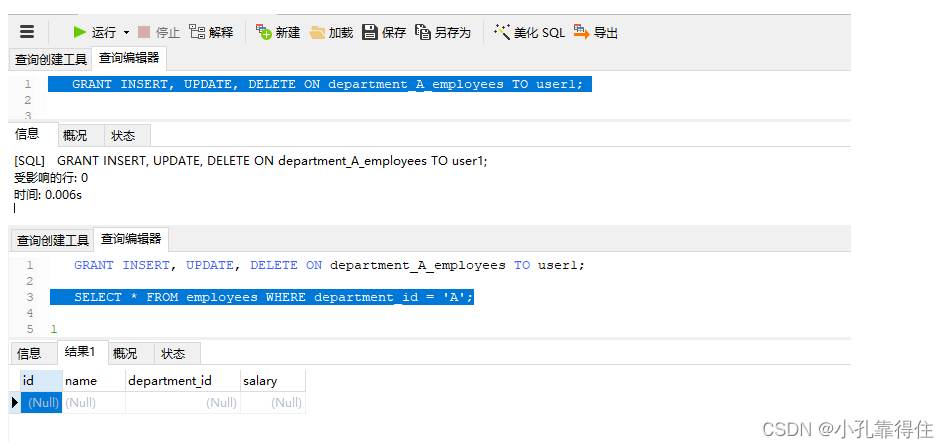
MySQL-视图:视图概述、使用视图注意点、视图是否影响基本表
视图 一、视图概述二、使用视图注意点三、视图操作是否影响基本表 一、视图概述 在数据库管理系统中,视图(View)是一种虚拟表,它并不实际存储数据,而是基于一个或多个实际表的查询结果。视图提供了一种对数据库中数据…...
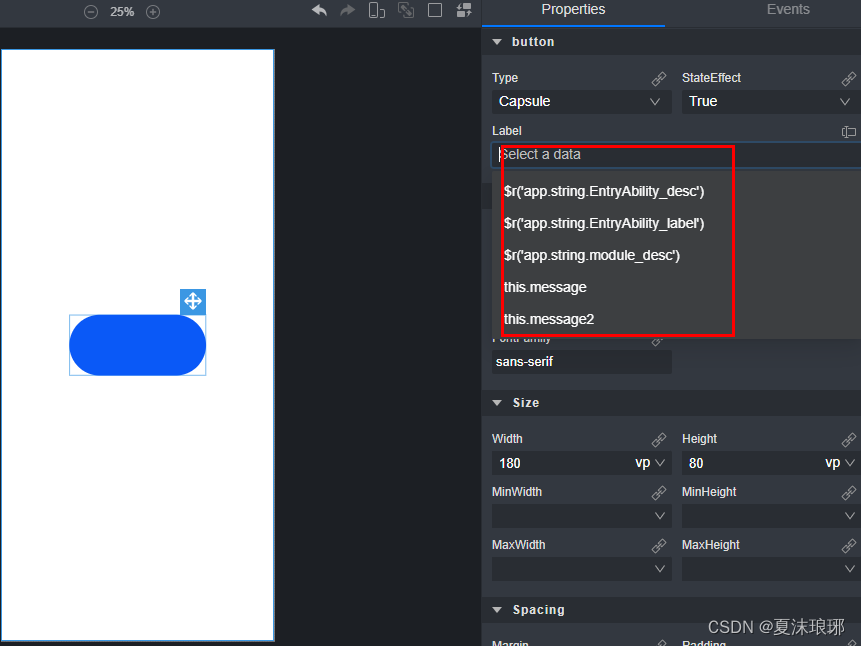
鸿蒙开发(四)-低代码开发
鸿蒙开发(四)-低代码开发 本文主要介绍下鸿蒙下的低代码开发。 鸿蒙低代码是指在鸿蒙操作系统进行应用开发时,采用简化开发流程和减少编码量的方式来提高开发效率。 1:开启低代码开发 首先我们打开DevEco Studio .然后创建工程。 如图所示ÿ…...
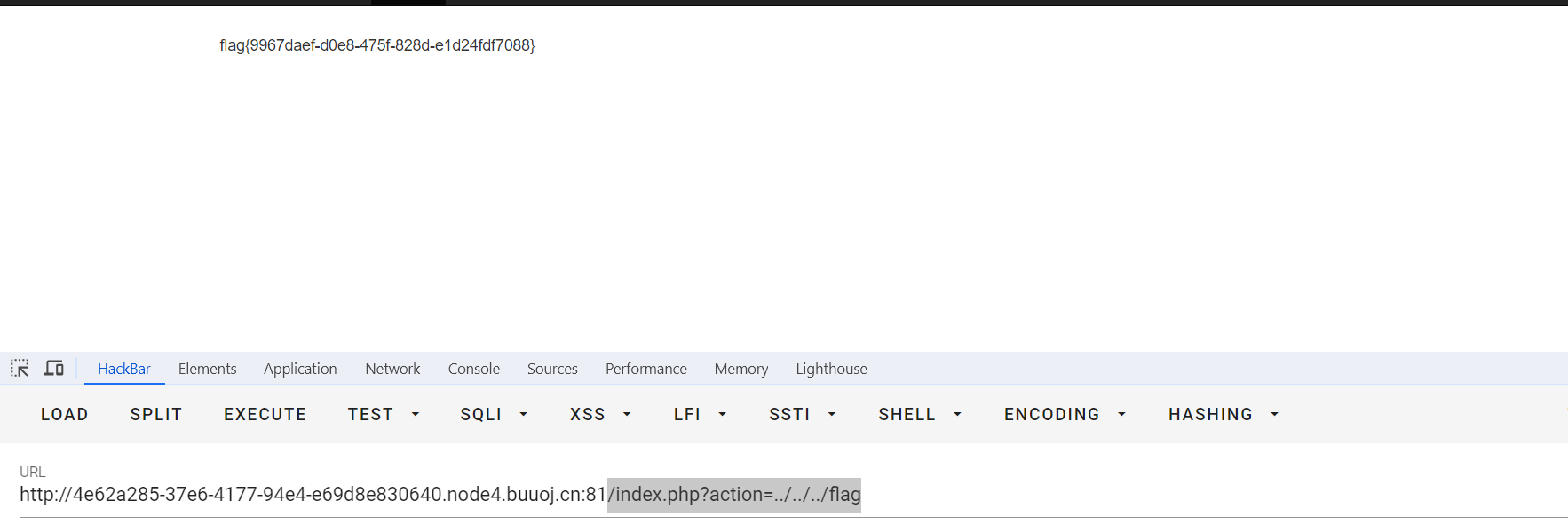
BUU [网鼎杯 2020 半决赛]AliceWebsite
BUU [网鼎杯 2020 半决赛]AliceWebsite 开题: hint附件是源码。在index.php中有一个毫无过滤的本地文件包含 <?php $action (isset($_GET[action]) ? $_GET[action] : home.php); if (file_exists($action)) {include $action; } else {echo "File not…...

超越 Siri 和 Alexa:探索LLM(大型语言模型)的世界
揭秘LLM:语言模型新革命,智能交互的未来趋势 近年来,虚拟助手的世界发生了重大转变。 虽然 Siri 和 Alexa 本身就是革命性的,但一种称为大型语言模型 (LLM) 的新型人工智能正在将虚拟助手的概念提升到一个全新的水平。 在这篇博文…...

Linux删除Mysql
//rpm包安装方式卸载 查包名:rpm -qa|grep -i mysql 删除命令:rpm -e –nodeps 包名//yum安装方式下载 1.查看已安装的mysql 命令:rpm -qa | grep -i mysql 2.卸载mysql 命令:yum remove mysql-community-server-5.6.36-2.el7.x86…...

CNN中常见的池化操作有哪些,作用是什么?
CNN中常见的池化操作有哪些,作用是什么? CNN中常见的池化操作只要是两种,平均值池化和最大值池化最大值池化常用于分类任务,是指在输入数据的局部区域内取最大值作为输出。最大池化的作用是降低特征图的尺寸,减少参数…...
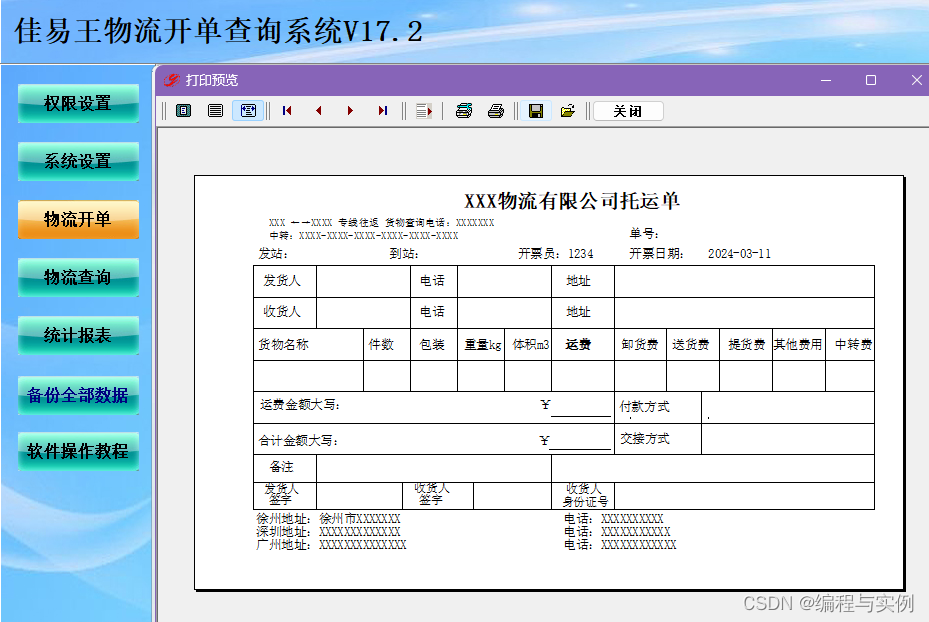
能打印单据的软件,如进出库单据,物流快运单据,定制单据样式
能打印单据的软件,如进出库单据,物流快运单据,定制单据样式 一、前言 软件文件下载可以点击最下方官网卡片——软件下载——试用版软件下载 1、不同行业打印的单据不同 2、同一个行业打印的样式可能不同 3、有的行业已经印刷好了许多打印…...
uniapp列表进入动画
app列表入场动画 - DCloud 插件市场 列表入场动画https://ext.dcloud.net.cn/plugin?id16957...

FPGA TestBench编写学习
1 timescale 1.1 简介 timescale指令用于指定编译器在处理仿真时的时间单位和时间精度。这个指令通常在模块的顶层声明中使用,它告诉编译器和仿真器如何解释代码中的时间值。 timescale指令的语法如下: timescale <time_unit> <time_precis…...

Centos7 安装mongoDB
下载安装包 curl -O https://fastdl.mongodb.org/linux/mongodb-linux-x86_64-3.2.12.tgz 解压 tar -zxvf mongodb-linux-x86_64-3.2.12.tgz移动到指定位置 mv mongodb-linux-x86_64-3.2.12/ /usr/local/mongodb在/usr/local/mongodb下创建文件夹 cd /usr/local/mongodb m…...
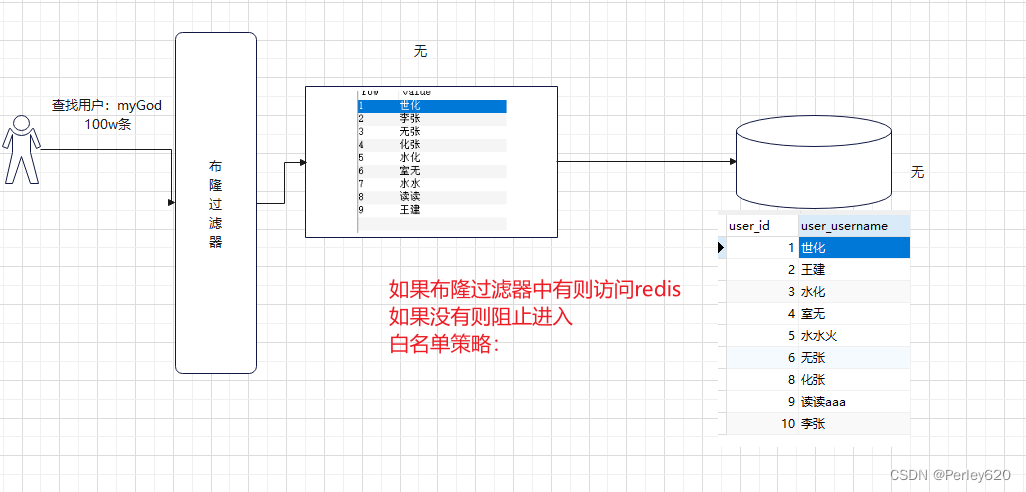
Redis冲冲冲——Redis持久化方式及其区别
目录 引出Redis持久化方式Redis入门1.Redis是什么?2.Redis里面存Java对象 Redis进阶1.雪崩/ 击穿 / 穿透2.Redis高可用-主从哨兵3.持久化RDB和AOF4.Redis未授权访问漏洞5.Redis里面安装BloomFilte Redis的应用1.验证码2.Redis高并发抢购3.缓存预热用户注册验证码4.R…...
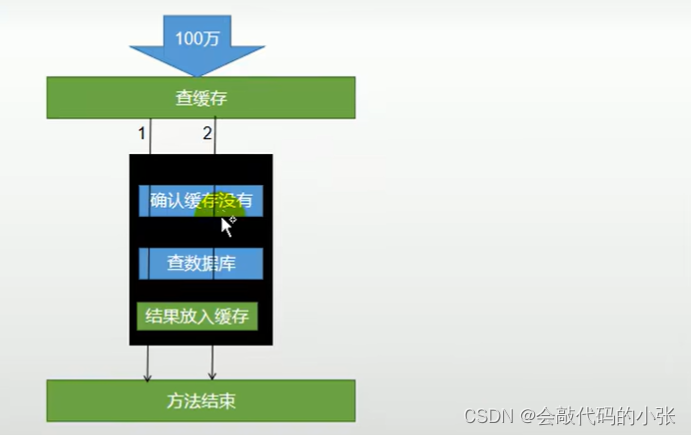
谷粒商城【成神路】-【10】——缓存
目录 🧂1.引入缓存的优势 🥓2.哪些数据适合放入缓存 🌭3.使用redis作为缓存组件 🍿4.redis存在的问题 🧈5.添加本地锁 🥞6.添加分布式锁 🥚7.整合redisson作为分布式锁 🚗…...

Facebook、亚马逊账号如何养号?
之前我们讨论过很多关于代理器的问题。它们的工作原理是什么?在不同的软件中要使用那些代理服务器?这些代理服务器之间的区别是什么?什么是反检测浏览器等等。 除了这些问题,相信很多人也会关心在使用不同平台的时代理器的选择问题。比如,为什么最好…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...
