【机器学习】支持向量机 | 支持向量机理论全梳理 对偶问题转换,核方法,软间隔与过拟合
支持向量机走的路和之前介绍的模型不同
之前介绍的模型更趋向于进行函数的拟合,而支持向量机属于直接分割得到我们最后要求的内容
1 支持向量机SVM基本原理
当我们要用一条线(或平面、超平面)将不同类别的点分开时,我们希望这条线尽可能地远离最靠近它的点。这些最靠近线的点被称为支持向量。而这条线到最靠近它的点的距离被称为间隔。支持向量机就是要找到一个最大间隔的线(或平面、超平面),这样可以更好地区分不同类别的点。
以下是支持向量机的一些关键概念和特性:
- 超平面:在二维空间中,超平面是一条直线;在三维空间中,它是一个平面;在更高维的空间中,超平面是一个超平面。对于一个二分类问题,超平面将特征空间划分为两个部分,每个部分对应一个类别。
- 支持向量:支持向量是离超平面最近的那些点。在SVM中,这些点对定义超平面起着重要作用,因为它们决定了超平面的位置。
- 间隔:支持向量到超平面的距离称为间隔。SVM的目标是找到具有最大间隔的超平面,这样可以更好地对新样本进行分类。
2 支持向量分类
2.1 支持向量机求解——对偶问题转换
在机器学习中,对偶问题是指将原始优化问题转化为另一个形式的问题。对于支持向量机(SVM)来说,对偶问题是通过对原始问题的拉格朗日函数进行求解得到的。
具体来说,原始的SVM优化问题是要最小化带有正则化项的损失函数。这个损失函数包括两部分:一部分是要使得分类间隔最大化,另一部分是要保证分类的准确性。直接求解这个问题可能比较复杂。为了简化求解过程,可以将原始问题转化为对偶问题。通过引入拉格朗日乘子,我们可以得到对偶问题。在对偶问题中,我们需要最大化一个关于拉格朗日乘子的函数,同时满足一些约束条件。
通过求解对偶问题,我们可以得到支持向量的拉格朗日乘子的最优解,然后可以使用这些乘子来计算权重向量和偏置,从而得到最终的分类超平面。
对偶问题满足KKT条件,KKT条件如下
KKT(Karush-Kuhn-Tucker)条件是最优化问题中的一组条件,用于描述在某些条件下最优解的性质。对于支持向量机(SVM)的对偶问题,KKT条件可以描述如下:
-
对偶互补条件:对于所有的 i i i,有 α i [ y i ( w T x i + b ) − 1 + ξ i ] = 0 \alpha_i [y_i (\mathbf{w}^T \mathbf{x}_i + b) - 1 + \xi_i] = 0 αi[yi(wTxi+b)−1+ξi]=0,即对所有的支持向量,乘子 α i \alpha_i αi不为零的条件下, y i ( w T x i + b ) − 1 + ξ i = 0 y_i (\mathbf{w}^T \mathbf{x}_i + b) - 1 + \xi_i = 0 yi(wTxi+b)−1+ξi=0,这表示支持向量的函数间隔与几何间隔之差等于1。
-
互补松弛条件:对于所有的 i i i,有 β i ξ i = 0 \beta_i \xi_i = 0 βiξi=0,即对所有的支持向量,松弛变量 ξ i \xi_i ξi不为零的条件下, β i = 0 \beta_i = 0 βi=0,表示松弛变量与 β i \beta_i βi之间的关系。
-
KKT条件:对于所有的 i i i,有 α i ≥ 0 \alpha_i \geq 0 αi≥0, y i ( w T x i + b ) − 1 + ξ i ≥ 0 y_i (\mathbf{w}^T \mathbf{x}_i + b) - 1 + \xi_i \geq 0 yi(wTxi+b)−1+ξi≥0, β i ≥ 0 \beta_i \geq 0 βi≥0, α i [ y i ( w T x i + b ) − 1 + ξ i ] = 0 \alpha_i [y_i (\mathbf{w}^T \mathbf{x}_i + b) - 1 + \xi_i] = 0 αi[yi(wTxi+b)−1+ξi]=0, β i ξ i = 0 \beta_i \xi_i = 0 βiξi=0。
KKT条件告诉我们,在最优解处,拉格朗日乘子和变量的取值必须满足这些条件。
基于KKT条件,更好求SVM的最优解
2.2 非线性问题——核方法
核方法是一种机器学习中常用的技术,特别是在支持向量机(SVM)等算法中经常使用。它的基本思想是通过一个非线性映射将原始的输入特征空间映射到一个更高维的特征空间,使得原本在低维空间中不可分的样本变得可分。这个非线性映射称为核函数,它可以避免在高维空间中进行实际的特征转换,从而节省计算成本。
在SVM中,核方法的主要作用是将样本从原始特征空间映射到一个更高维的空间,在这个高维空间中找到一个线性超平面来分割不同类别的样本。常用的核函数包括线性核、多项式核、高斯核(也称为径向基函数核)等,它们可以根据数据的特点选择合适的核函数来提高分类的准确性。
核方法的优势在于能够处理非线性可分的数据,同时避免了在高维空间中进行实际的特征转换,从而降低了计算复杂度。因此,核方法在机器学习中被广泛应用于分类、回归和聚类等任务中。
映射的时候,我们需要核函数进行映射
核函数是支持向量机(SVM)中的重要概念,它允许在高维空间中进行非线性分类。在SVM中,我们希望找到一个最优超平面来将不同类别的数据点分开。如果数据在原始特征空间中不是线性可分的,那么就需要使用核函数将数据映射到一个高维特征空间,使得数据在该空间中线性可分。
核函数的主要思想是,我们可以通过一个函数来计算两个向量在高维空间中的内积,而不必显式地计算它们在高维空间中的表示。这样做的好处是,可以避免在高维空间中显式地存储和计算数据,而是利用核函数的性质,只需计算原始特征空间中的内积,就可以得到在高维空间中的内积。这种技术称为“核技巧”。
常用的核函数包括:
- 线性核函数: K ( x i , x j ) = x i T x j K(\mathbf{x}_i, \mathbf{x}_j) = \mathbf{x}_i^T \mathbf{x}_j K(xi,xj)=xiTxj,直接计算两个向量在原始特征空间中的内积。
- 多项式核函数: K ( x i , x j ) = ( γ x i T x j + r ) d K(\mathbf{x}_i, \mathbf{x}_j) = (\gamma \mathbf{x}_i^T \mathbf{x}_j + r)^d K(xi,xj)=(γxiTxj+r)d,将数据映射到多项式特征空间。
- 高斯核函数(径向基函数核): K ( x i , x j ) = exp ( − γ ∥ x i − x j ∥ 2 ) K(\mathbf{x}_i, \mathbf{x}_j) = \exp(-\gamma \|\mathbf{x}_i - \mathbf{x}_j\|^2) K(xi,xj)=exp(−γ∥xi−xj∥2),将数据映射到无穷维的特征空间,适用于非线性可分的情况。
通过使用核函数,SVM可以在高维空间中进行复杂的非线性分类,而不必显式地计算和存储高维数据。核函数的选择通常基于对数据特征的理解和试验结果。
2.3 防止过拟合——软间隔与正则化
软间隔是支持向量机(SVM)中的概念,用于处理线性不可分的情况。在标准的线性可分SVM中,我们希望找到一个最优超平面,将不同类别的数据点完全分开。然而,在现实应用中,数据往往不是完全线性可分的,即存在一些噪音或异常点。为了处理这种情况,引入了软间隔的概念。
软间隔允许一些数据点位于超平面的错误一侧,但是通过引入一个惩罚项,希望这些错误被最小化。具体来说,软间隔SVM的优化问题包括两部分:最小化误分类点的数量(间隔违例)和最大化间隔。
软间隔SVM的优化问题可以形式化如下:
m i n w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ξ i min_{\mathbf{w}, b, \xi} \frac{1}{2} \|\mathbf{w}\|^2 + C \sum_{i=1}^{m} \xi_i minw,b,ξ21∥w∥2+C∑i=1mξi
subject to y i ( w T x i + b ) ≥ 1 − ξ i , ξ i ≥ 0 , ∀ i \text{subject to } y_i (\mathbf{w}^T \mathbf{x}_i + b) \geq 1 - \xi_i, \quad \xi_i \geq 0, \quad \forall i subject to yi(wTxi+b)≥1−ξi,ξi≥0,∀i
其中, w \mathbf{w} w是超平面的法向量, b b b是偏置项, ξ i \xi_i ξi是松弛变量, C C C是正则化参数,用于控制间隔违例的惩罚力度。优化问题的目标是要找到一个最优的超平面,以及对应的 ξ i \xi_i ξi,使得误分类的点尽量少,同时间隔尽量大。
软间隔SVM通过调节正则化参数 C C C可以在偏向于过拟合( C C C较小)和偏向于欠拟合( C C C较大)之间进行平衡,从而在实际应用中取得更好的性能。
2 支持向量回归
支持向量回归(Support Vector Regression,SVR)是支持向量机(SVM)的一种应用,用于解决回归问题。与传统的线性回归方法不同,SVR可以处理非线性关系,并且对异常值具有较强的鲁棒性。
SVR的基本思想与支持向量分类(SVC)类似,都是通过寻找一个最优的超平面(或者称为回归器)来拟合数据。与SVC不同的是,SVR的目标是最小化预测误差,而不是最大化间隔。
SVR的优化问题可以形式化如下:
min w , b , ξ , ξ ∗ 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ( ξ i + ξ i ∗ ) \min_{\mathbf{w}, b, \xi, \xi^*} \frac{1}{2} \|\mathbf{w}\|^2 + C \sum_{i=1}^{m} (\xi_i + \xi_i^*) minw,b,ξ,ξ∗21∥w∥2+C∑i=1m(ξi+ξi∗)
subject to { y i − w T ϕ ( x i ) − b ≤ ε + ξ i ∗ w T ϕ ( x i ) + b − y i ≤ ε + ξ i ξ i , ξ i ∗ ≥ 0 \text{subject to } \begin{cases} y_i - \mathbf{w}^T \phi(\mathbf{x}_i) - b \leq \varepsilon + \xi_i^* \\ \mathbf{w}^T \phi(\mathbf{x}_i) + b - y_i \leq \varepsilon + \xi_i \\ \xi_i, \xi_i^* \geq 0 \end{cases} subject to ⎩ ⎨ ⎧yi−wTϕ(xi)−b≤ε+ξi∗wTϕ(xi)+b−yi≤ε+ξiξi,ξi∗≥0
其中, w \mathbf{w} w是回归器的权重向量, b b b是偏置项, ξ i \xi_i ξi和 ξ i ∗ \xi_i^* ξi∗是松弛变量, ε \varepsilon ε是一个预先指定的参数,称为容忍度, C C C是正则化参数。
SVR的核心思想是通过最小化间隔违例( ξ i \xi_i ξi和 ξ i ∗ \xi_i^* ξi∗)的同时,尽可能保持间隔边缘,从而找到一个最优的超平面来拟合数据。支持向量是那些落在间隔边缘上的数据点,它们对于定义超平面和拟合模型起着关键作用。
总的来说,SVR通过引入间隔违例和正则化参数,可以在保持模型简单性的同时,有效地拟合非线性关系,并且对异常值具有较好的鲁棒性。
相关文章:

【机器学习】支持向量机 | 支持向量机理论全梳理 对偶问题转换,核方法,软间隔与过拟合
支持向量机走的路和之前介绍的模型不同 之前介绍的模型更趋向于进行函数的拟合,而支持向量机属于直接分割得到我们最后要求的内容 1 支持向量机SVM基本原理 当我们要用一条线(或平面、超平面)将不同类别的点分开时,我们希望这条…...

【JS】APIs:事件流、事件委托、其他事件、页面尺寸、日期对象与节点操作
1 事件流 捕获阶段:从父到子 冒泡阶段:从子到父 1.1 事件捕获 <body> <div class"fa"><div class"son"></div> </div> <script>const fadocument.querySelector(.fa);const sondocument.qu…...

定制红酒:如何根据客户需求调整红酒口感与风格
在云仓酒庄洒派,云仓酒庄洒派深知不同消费者对于红酒的口感与风格有着不同的喜好和需求。因此,云仓酒庄洒派根据消费者的具体要求,灵活调整红酒的口感与风格,以满足他们的期望。 首先,云仓酒庄洒派会与消费者进行深入的…...

利用excel批量修改图片文件名
今天同事提出需求要实现利用excel批量修改某文件夹下的图片重命名,衡量到各种条件,最后还是选择了vbs来实现。代码如下 代码 创建Excel对象 Set objExcel CreateObject("Excel.Application") objExcel.Visible False 隐藏Excel窗口 打开Ex…...
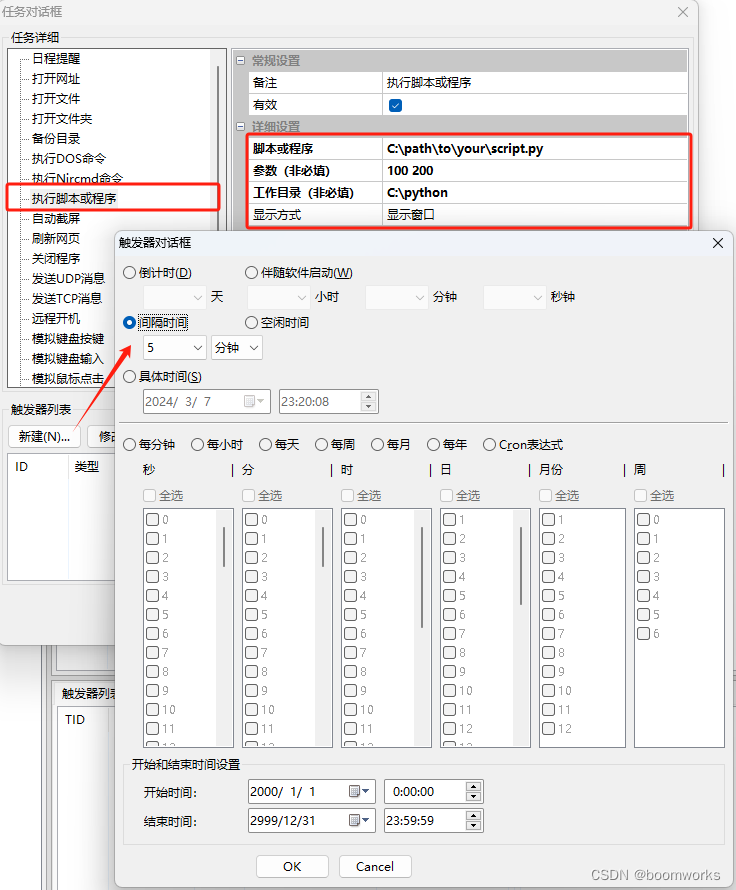
间隔5分钟执行1次Python脚本设置步骤 —— 定时执行专家
《定时执行专家》是一款制作精良、功能强大、毫秒精度、专业级的定时任务执行软件,用于在 Windows 系统上定时执行各种任务,包括执行脚本或程序。 下面是使用 "定时执行专家" 软件设置定时执行 Python 脚本的步骤: 步骤 1: 设置 P…...
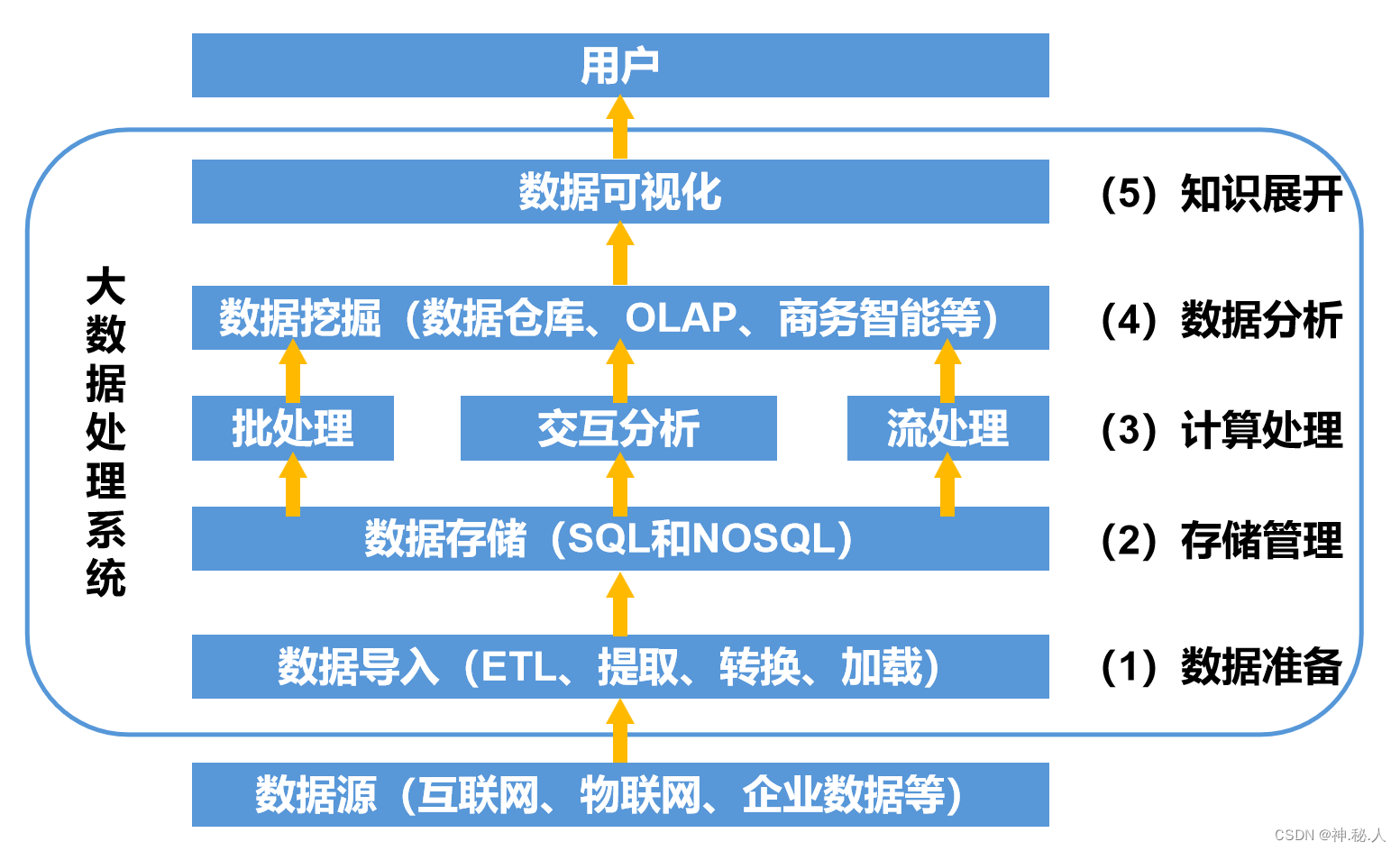
计算机网络基础【信息系统监理师】
计算机网络基础【信息系统监理师】 1、OSI七层参考模型2、TCP/IP协议3、网络拓扑结构分类4、网络传输介质分类5、网络交换技术6、网络存储技术7、网络规划技术8、综合布线系统8.1、综合布线工程内容8.1、隐蔽工程-金属线槽安装8.2、隐蔽工程-管道安装槽道与各种管线间的最小净距…...

网络安全风险评估:详尽百项清单要点
网络安全风险评估是识别、分析和评估组织信息系统、网络和资产中潜在风险和漏洞的系统过程。主要目标是评估各种网络威胁和漏洞的可能性和潜在影响,使组织能够确定优先顺序并实施有效的安全措施来减轻这些风险。该过程包括识别资产、评估威胁和漏洞、分析潜在影响以…...
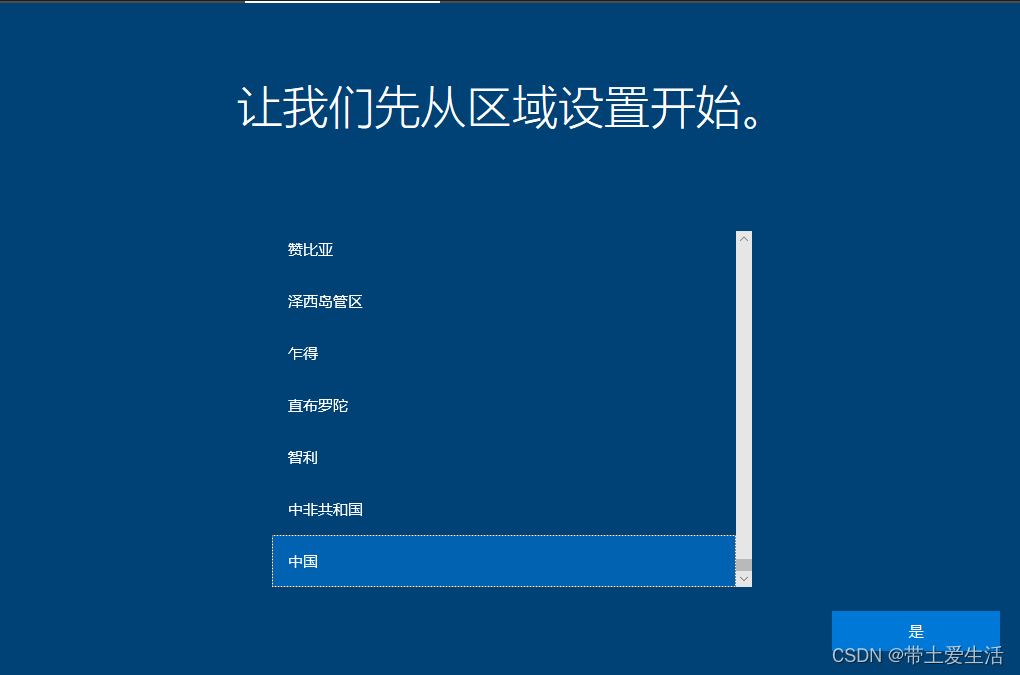
不会用虚拟机装win10?超详细教程解决你安装中的所有问题!
前言:安装中有任何疑问,可以在评论区提问,博主身经百战会快速解答小伙伴们的疑问 BT、迅雷下载win10镜像(首先要下载win10的镜像):ed2k://|file|cn_windows_10_business_editions_version_1903_updated_sep…...

洛谷 素数环 Prime Ring Problem
题目描述 PDF 输入格式 输出格式 题意翻译 输入正整数 nn,把整数 1,2,\dots ,n1,2,…,n 组成一个环,使得相邻两个整数之和均为素数。输出时,从整数 11 开始逆时针排列。同一个环恰好输出一次。n\leq 16n≤16,保证一定有解。 多…...
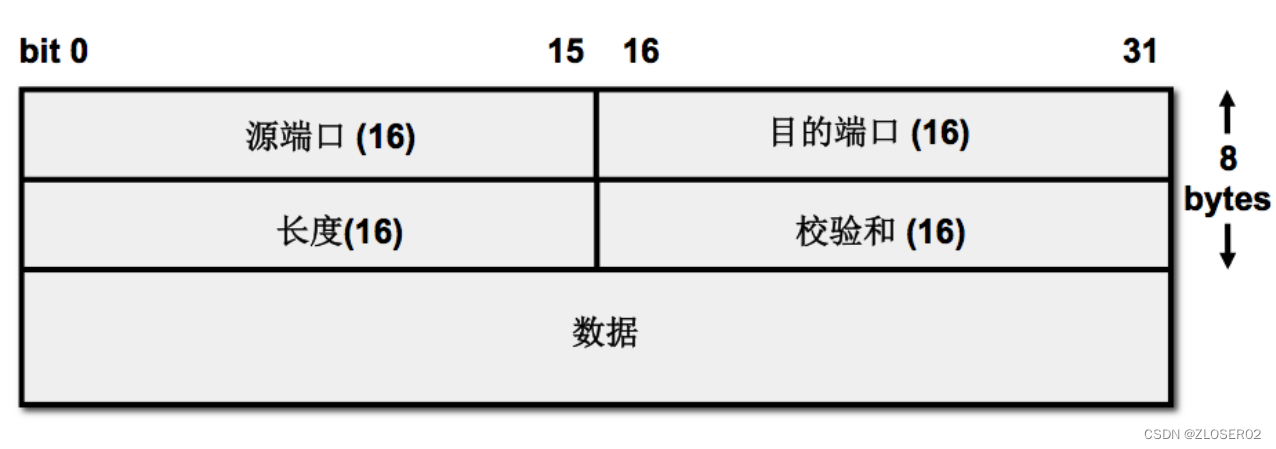
【DPDK】基于dpdk实现用户态UDP网络协议栈
文章目录 一.背景及导言二.协议栈架构设计1. 数据包接收和发送引擎2. 协议解析3. 数据包处理逻辑 三.网络函数编写1.socket2.bind3.recvfrom4.sendto5.close 四.总结 一.背景及导言 在当今数字化的世界中,网络通信的高性能和低延迟对于许多应用至关重要。而用户态网…...

开源好用的所见即所得(WYSIWYG)编辑器:Editor.js
文章目录 特点基于区块干净的数据 界面与交互插件标题和文本图片列表Todo表格 使用安装创建编辑器实例配置工具本地化自定义样式 今天介绍一个开源好用的Web所见即所得(WYSIWYG)编辑器: Editor.js Editor.js 是一个基于 Web 的所见即所得富文本编辑器,它…...

sqlite 损坏 修复
步骤1 SQLite Download Page下载sqlite3 对应的系统版本 2.参考怎么恢复sqlite 数据库文件✅ - 有乐数据恢复网 sqlite3 dbname > .mode insert > .output dbdump.sql > .dump > .exit 恢复方法1 1.创建一个新的数据库 例如名字叫 test.db 2sqlite3 test.…...
初学Vue——Vue路由
0 什么是Vue路由 类似于Html中的超链接(<a>)一样,可以跳转页面的一种方式。 前端路由:URL中hash(#号之后的内容)与组件之间的对应关系,如下图: 当我们点击左侧导航栏时,浏览器的地址栏会发生变化,路…...
如何使用宝塔面板搭建Discuz并结合cpolar实现远程访问本地论坛
文章目录 前言1.安装基础环境2.一键部署Discuz3.安装cpolar工具4.配置域名访问Discuz5.固定域名公网地址6.配置Discuz论坛 前言 Crossday Discuz! Board(以下简称 Discuz!)是一套通用的社区论坛软件系统,用户可以在不需要任何编程的基础上&a…...

llc的基波分析法
对于我们之前分析的 LLC等效谐振电路的分析,其实我们发现分析的并不是完整的方波输入,而是用正弦波来分的 那么为何用基波来分析呢,因为对于方波而言,根据傅里叶级数它是可以分解成基波、 1次、3次、5次.......等各种奇次谐波的入…...
一键清除JavaScript代码中的注释:使用正则表达式实现
这个正则表达式可以有效地匹配 JavaScript 代码中的各种注释,并且跳过了以 http: 或 https: 开头的链接。 /\/\*[\s\S]*?\*\/|\/\/[^\n]*|<!--[\s\S]*?-->|(?<!http:|https:)\/\/[^\n]*/gvscode 实战,ctrlF 调出查找替换工具,点…...
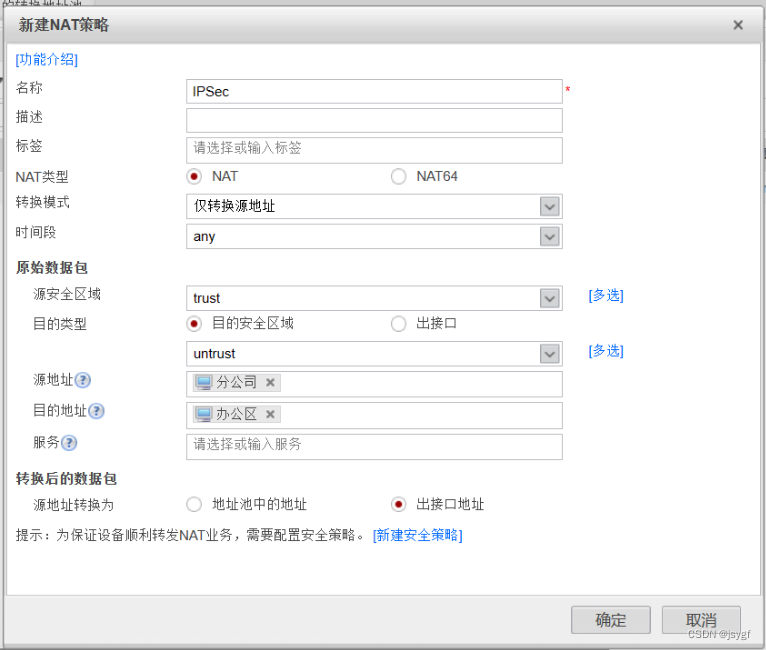
第七次作业
IPSEC VPPN实验配置 目标:在FW5和FW3之间建立一条IPSEC通道,保证10.0.2.0/24网段可以正常访问到192.168.1.0/24 1.FW1和FW2进行双机热备(之前实验没保存,可看上个实验) 还有一些配置前面实验有。 2.场景选择点对点…...

在jupyternotebook中,如何解决作图时负号无法显示的问题?
输入以下代码即可。 import matplotlib as mpl mpl.rcParams[axes.unicode_minus] False 原文链接:在jupyternotebook中,如何解决作图时负号无法显示的问题?...

ConnectionResetError: [WinError 10054] 远程主机强迫关闭了一个现有的连接。
发生的错误信息: File "C:\Users\malongqiang\.conda\envs\ObjectDetection\lib\ssl.py", line 1309, in do_handshakeself._sslobj.do_handshake() ConnectionResetError: [WinError 10054] 远程主机强迫关闭了一个现有的连接。 分析原因: …...

主流开发语言与环境介绍
主流开发语言与环境介绍 1. 引言 随着计算机科学的不断发展,各种编程语言和开发环境层出不穷。选择一种适合自己的主流开发语言和环境是每个开发者都必须面临的问题。本文将为大家介绍几种目前最为流行的主流开发语言和环境,帮助读者选择合适的工具进行…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
