C语言分析基础排序算法——插入排序
目录
插入排序
直接插入排序
希尔排序
希尔排序基本思路解析
希尔排序优化思路解析
完整希尔排序文件
插入排序
直接插入排序
所谓直接插入排序,即每插入一个数据和之前的数据进行大小比较,如果较大放置在后面,较小放置在前面,具体思路分析如下:
//以下面的数组为例
int data[] = { 23,34,84,99,67,26,21,89 };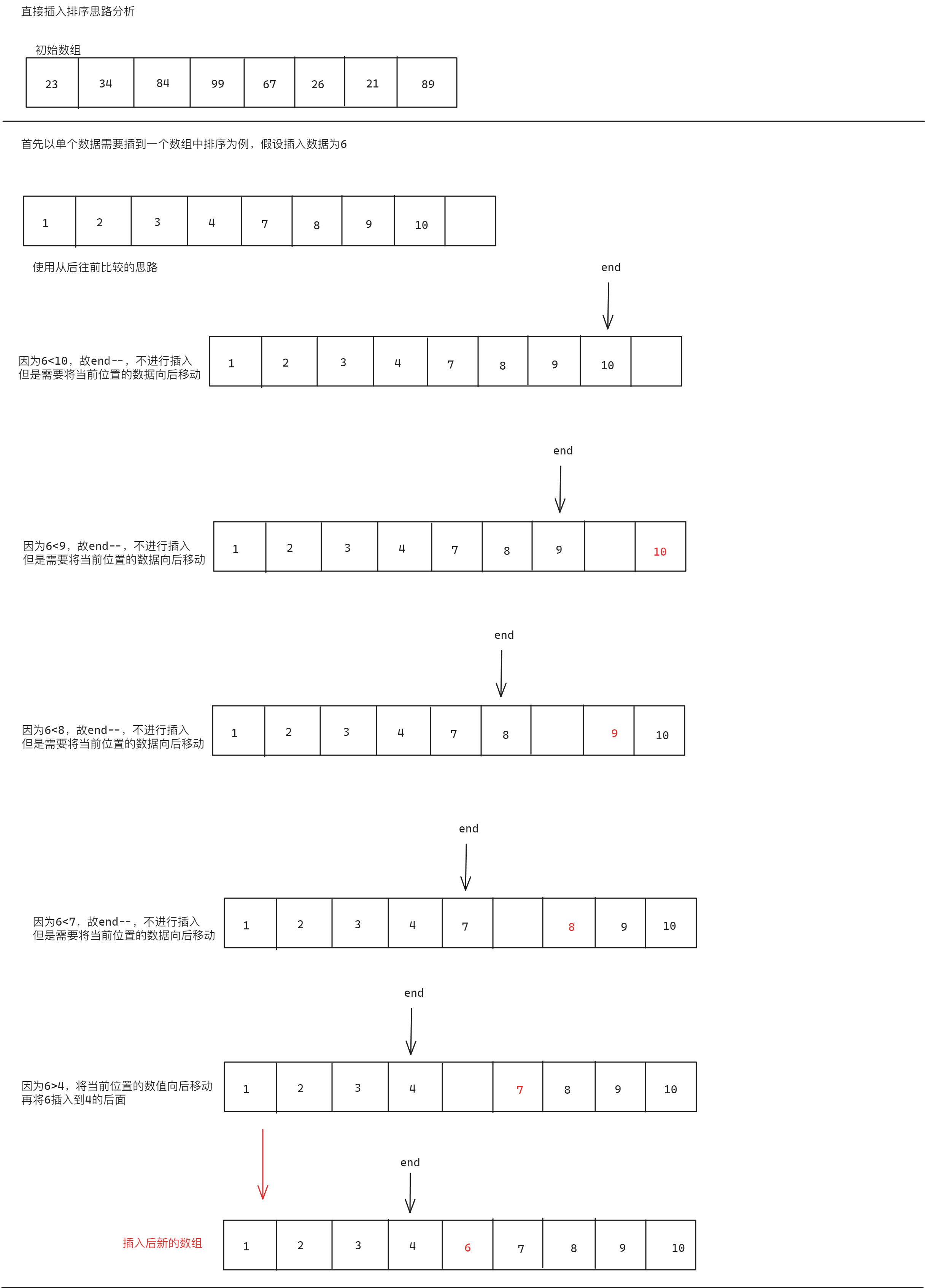
参考代码
#define _CRT_SECURE_NO_WARNINGS 1#include <stdio.h>void DirectInsert_sort(int* data, int sz)
{// 遍历数组for (int i = 1; i < sz; i++){int tmp = data[i];//获取数组的当前元素int end = i - 1;//获取数组的当前元素的上一个元素//当遇到比tmp大数值时,挪动数据,直到遇到比当前数据小的数据时跳出循环while (end >= 0){if (data[end] > tmp){data[end + 1] = data[end];end--;}else{break;}}//在end的后一个位置插入数据,插入完毕后直接更新i和end继续比较data[end + 1] = tmp;}
}int main()
{int data[] = { 23,34,84,99,67,26,21,89 };int sz = sizeof(data) / sizeof(int);DirectInsert_sort(data, sz);//打印排序后的数组for (int i = 0; i < sz; i++){printf("%d ", data[i]);}return 0;
}
输出结果:
21 23 26 34 67 84 89 99通过分析可以得出直接插入排序在最坏的情况下(数据为完全逆序的状态)时间复杂度为O(N2),而在最好的情况下(已经为有序状态,只需要遍历一遍数据即可),时间复杂度为O(N)
希尔排序
希尔排序基本思路解析
希尔排序的基本思路是将一组数据按照间隔值gap分成gap组,对各组进行插入排序,这一步被称作预排序,接着再使用直接插入排序对整体再进行一次排序,具体过程如下

//希尔排序基础思路
void ShellSort(int* data, int sz)
{int gap = 3;//首先进行三组预排序for (int i = 0; i < gap; i++){//每一组的排序for (int j = gap + i; j < sz; j += gap){int end = j - gap;int tmp = data[j];while (end >= 0){if (data[end] > tmp){data[end + gap] = data[end];end -= gap;}else{break;}}data[end + gap] = tmp;}}//最后进行整体插入排序gap = 1;for (int i = gap; i < sz; i += gap){int end = i - 1;int tmp = data[i];while (end >= 0){if (data[end] > tmp){data[end + gap] = data[end];end--;}else{break;}}data[end + gap] = tmp;}
}希尔排序优化思路解析
以上思路只是简单的分析,接下来对细节进行分析优化,具体思路如下
首先是间隔值gap,gap决定了分组的数量,也间接决定了最大值走到最后需要的次数,当gap特别大时,最大值很快就会到数据的最末尾,但是同时整体越不接近需要的升序;相反,当gap特别小时,最大值到数据末尾的次数变多,同时整体越接近有序,所以gap数值不容易确定,但是一般取gap为整体的1/3或者取1/2,即gap = size / 3或gap = size / 2 (size是数组长度)
第二个问题,如果将预排序和最后的插入排序分开写,那么需要写五个循环,三层循环解决预排序,两层循环解决最后的插入排序,所以可以考虑将预排序与直接插入排序放在一起,达到在同一个循环中解决问题
可以考虑将每一次循环变量移动的位置改为移动一位,代替原来的一次移动gap位,如下图所示
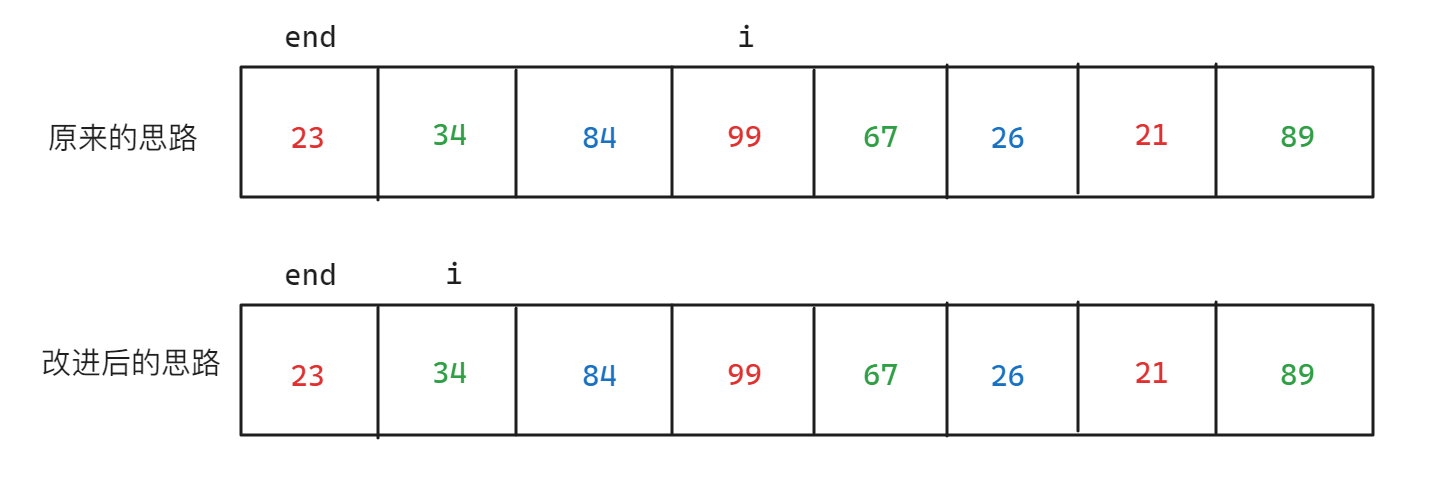
而改进后的思路与原来的思路对比:原来的思路是先排一组,排完一组后再排第二组,而改进后的思路是遇到i当前位置是哪一组的就排哪一组的数据,但是需要注意的是,当前的tmp所在位置为下一个相差gap的位置,该位置需要有确切的数值可以与end进行比较,所以tmp不能越界,假设当前tmp为3,数组最大下标为7,也就是tmp所在的下标最大只能为7,即i + gap不能超过7,故i最大只能为4,所以i不能超过5
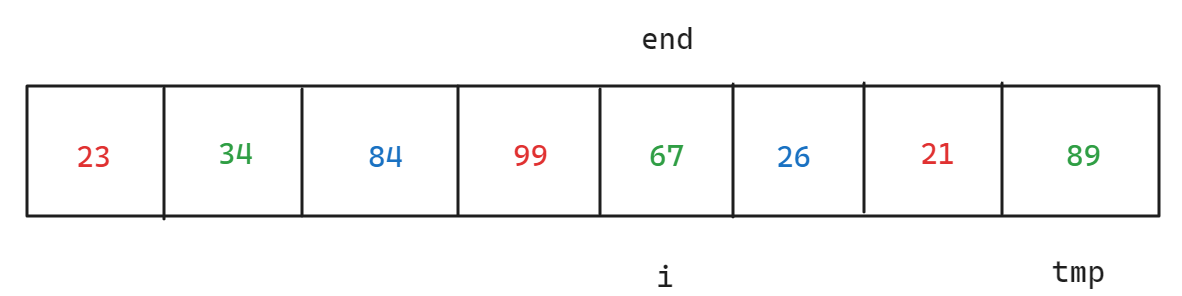
接下来是如何处理预排序和之后的直接排序放在一起的问题,对于这个问题,首先就是gap不能为一个固定值,如果gap为固定的某一个数值,例如3,那么预排序和直接插入排序还是需要两组循环才能解决,鉴于gap最后需要回到1,可以考虑从gap/3分组开始,当预排序完gap为3的一组时,接下来排gap为2的一组,最后着排gap为1的一组,因为第一次gap为3时已经将数据处理了一遍,而gap数值越小,就会使预排序的结果更接近预期的排序结果,所以可以考虑gap = gap / 3,每执行完一次预排序就更换一次gap间隔值,从而达到预排序与最后的直接插入排序放在一起,因为当gap为1时也可以满足预排序的思路,故放在一起也不会有任何冲突,只是间隔值从3变成了1,但是需要注意一个问题,当gap小于3时,gap最后的商为0,导致gap无法取到1,所以需要写成gap = gap / 3 + 1
//希尔排序优化思路
void ShellSort_modified(int* data, int sz)
{int gap = sz;while (gap > 1){gap = gap / 3 + 1;// 此处加1是为了确保最后一个gap一定为1,因为最后的直接插入排序是整体各自比较for (int i = 0; i < sz - gap; i++){int end = i;int tmp = data[i + gap];while (end >= 0){if (data[end] > tmp){data[end + gap] = data[end];end -= gap;}else{break;}}data[end + gap] = tmp;}}
}完整希尔排序文件
#define _CRT_SECURE_NO_WARNINGS 1#include <stdio.h>//希尔排序优化思路
void ShellSort_modified(int* data, int sz)
{int gap = sz;while (gap > 1){gap = gap / 3 + 1;// 此处加1是为了确保最后一个gap一定为1,因为最后的直接插入排序是整体各自比较for (int i = 0; i < sz - gap; i++){int end = i;int tmp = data[i + gap];while (end >= 0){if (data[end] > tmp){data[end + gap] = data[end];end -= gap;}else{break;}}data[end + gap] = tmp;}}
}int main()
{int data[] = { 23,34,84,99,67,26,21,89 };int sz = sizeof(data) / sizeof(int);ShellSort_modified(data, sz);for (int i = 0; i < sz; i++){printf("%d ", data[i]);}return 0;
}
输出结果:
21 23 26 34 67 84 89 99希尔排序总结:
- 希尔排序是对直接插入排序的优化
- 当
gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比 - 希尔排序的时间复杂度不好计算,因为
gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定
相关文章:

C语言分析基础排序算法——插入排序
目录 插入排序 直接插入排序 希尔排序 希尔排序基本思路解析 希尔排序优化思路解析 完整希尔排序文件 插入排序 直接插入排序 所谓直接插入排序,即每插入一个数据和之前的数据进行大小比较,如果较大放置在后面,较小放置在前面&#x…...
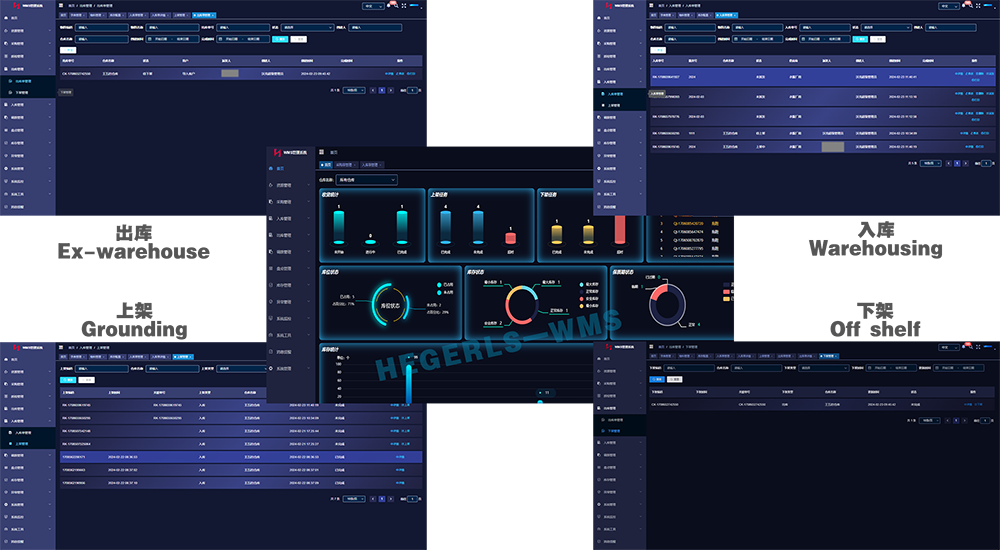
海格里斯HEGERLS智能托盘四向车系统为物流仓储自动化升级提供新答案
随着实体企业面临需求多样化、订单履行实时化、商业模式加速迭代等挑战,客户对物流仓储解决方案的需求也逐渐趋向于柔性化、智能化。作为近十年来发展起来的新型智能仓储设备,四向车系统正是弥补了先前托盘搬运领域柔性解决方案的空白。随着小车本体设计…...

SQLiteC/C++接口详细介绍-sqlite3类(一)
上一篇:SQLiteC/C接口简介 下一篇:SQLiteC/C接口详细介绍(二) 引言: SQLite C/C 数据库接口是一个流行的SQLite库使用形式,它允许开发者在C和C代码中嵌入 SQLite 基本功能的解决方案。通过 SQLite C/C 数据…...
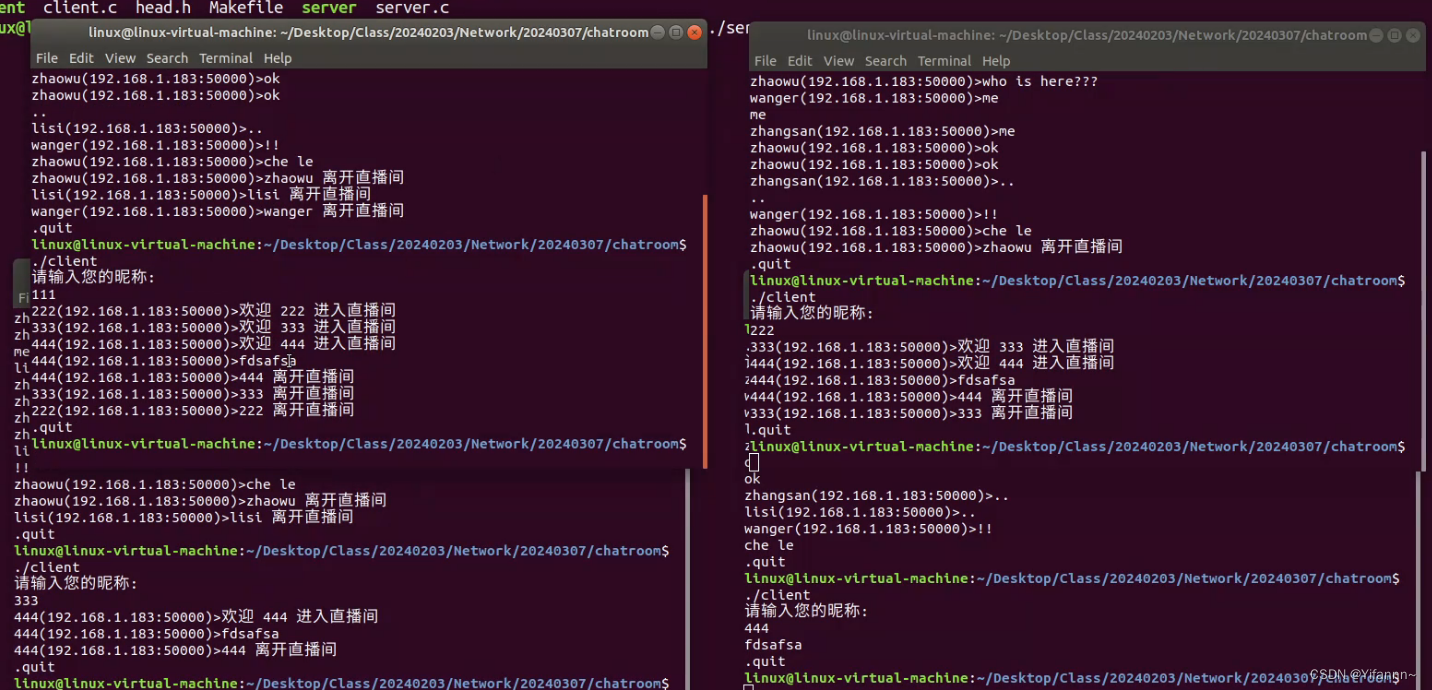
基于UDP实现直播间聊天的功能
需求:软件划分为用户客户端和主播服务端两个软件client.c和server.c 用户客户端负责:1.接收用户的昵称2.接收用户输入的信息,能够将信息发送给服务端3.接收服务端回复的数据信息,并完成显示主播服务端负责:1.对所有加入直播间的用…...

html5cssjs代码 006 文章排版《桃花源记》
html5&css&js代码 006 文章排版《桃花源记》 一、代码二、解释页面整体结构:头部信息:CSS样式:文章内容: 这段代码定义了一个网页,用于展示文章《桃花源记》的内容。网页使用了CSS样式来定义各个部分的显示效果…...

勾八头歌之数据科学导论—数据采集实战
一、数据科学导论——数据采集基本概念 第1关:巧妇难为无米之炊 第2关:数据采集概念与内涵 二、数据科学导论——数据采集实战 第1关:单网页爬取 import urllib.request import csv import re# ********** Begin ********** # dataurllib.r…...
微信小程序云开发教程——墨刀原型工具入门(素材面板)
引言 作为一个小白,小北要怎么在短时间内快速学会微信小程序原型设计? “时间紧,任务重”,这意味着学习时必须把握微信小程序原型设计中的重点、难点,而非面面俱到。 要在短时间内理解、掌握一个工具的使用…...

C#与WPF通用类库
个人集成封装,仓库已公开 NetHelper 集成了一些常用的方法; 如通用的缓存静态操作类、常用的Wpf的ValueConverters、内置的委托类型、通用的反射加载dll操作类、Wpf的ViewModel、Command、Navigation、Messenger、部分常用UserControls(可绑定的Passwo…...
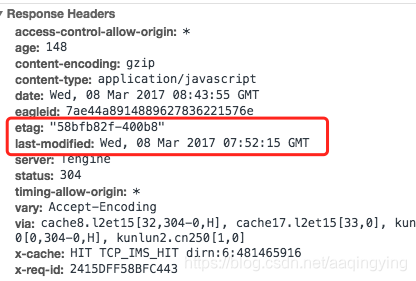
http协议中的强缓存与协商缓存,带图详解
此篇抽自本人之前的文章:http面试题整理 。 别急着跳转,先把缓存知识学会了~ http中的缓存分为两种:强缓存、协商缓存。 强缓存 响应头中的 status 是 200,相关字段有expires(http1.0),cache-control&…...

蓝桥杯2019年第十届省赛真题-修改数组
查重类题目,想到用标记数组记录是否出现过 但是最坏情况下可能会从头找到小尾巴,时间复杂度O(n2),数据范围106显然超时 再细看下题目,我们重复进行了寻找是否出现过,干脆把每个元素出现过的次数k记录下来,直…...
【Python使用】python高级进阶知识md总结第3篇:静态Web服务器-返回指定页面数据,静态Web服务器-多任务版【附代码文档】
python高级进阶全知识知识笔记总结完整教程(附代码资料)主要内容讲述:操作系统,虚拟机软件,Ubuntu操作系统,Linux内核及发行版,查看目录命令,切换目录命令,绝对路径和相对…...
ELK 日志分析系统
ELK (Elasticsearch、Logstash、Kibana)日志分析系统的好处是可以集中查看所有服务器日志,减轻了工作量,从安全性的角度来看,这种集中日志管理可以有效查询以及跟踪服务器被攻击的行为。 Elasticsearch 是个开源分布式…...

机器学习模型—逻辑回归
机器学习模型—逻辑回归 逻辑回归是一种用于分类任务的监督机器学习算法,其目标是预测实例属于给定类别的概率。逻辑回归是一种分析两个数据因素之间关系的统计算法。本文探讨了逻辑回归的基础知识、类型和实现。 什么是逻辑回归 逻辑回归用于二元分类,其中我们使用sigmoi…...

Ubuntu20.04 创建新的用户
1、了解Linux目录结构 推荐看一下:https://www.runoob.com/linux/linux-system-contents.html Linux支持多个用户进行操作的,这样提高了系统的安全性,也可以多人共用一个系统,不过要注意的是系统中安装的软件相关路径࿰…...

大数据入门之hadoop学习
大数据 1. 学习hadoop之前,我们先了解一下什么是大数据? 大数据通常指的是数据集规模非常庞大且难以在常规数据库和数据处理工具中有效处理的数据。 大数据的特点: 容量:大数据具有庞大的规模,远远超出了传统数据库和…...
MySQL安装使用(mac、windows)
目录 macOS环境 一、下载MySQL 二、环境变量 三、启动 MySql 四、初始化密码设置 windows环境 一、下载 二、 环境配置 三、安装mysql 1.初始化mysql 2.安装Mysql服务 3.更改密码 四、检验 1.查看默认安装的数据库 2.其他操作 macOS环境 一、下载MySQL 打开 MyS…...
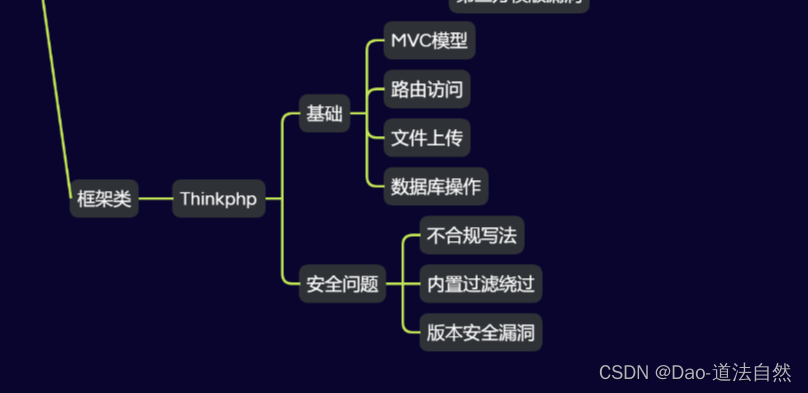
Day27:安全开发-PHP应用TP框架路由访问对象操作内置过滤绕过核心漏洞
目录 TP框架-开发-配置架构&路由&MVC模型 TP框架-安全-不安全写法&版本过滤绕过 思维导图 PHP知识点 功能:新闻列表,会员中心,资源下载,留言版,后台模块,模版引用,框架开发等 技…...
c++: 引用能否替代指针? 详解引用与指针的区别.
文章目录 前言1. 引用和指针的最大区别:引用不能改变指向2. 引用和指针在底层上面是一样的3. 引用和指针在sizeof面前大小不同4. 有多级指针,没有多级引用5.引用是引用的实体,指针会向后偏移同一个类型的大小 总结 前言 新来的小伙伴如果不知道引用是什么?可以看我的上一篇文…...

Java项目源码基于springboot的家政服务平台的设计与实现
大家好我是程序员阿存,在java圈的辛苦码农。辛辛苦苦板砖,今天要和大家聊的是一款Java项目源码基于springboot的家政服务平台的设计与实现,项目源码以及部署相关请联系存哥,文末附上联系信息 。 项目源码:Java基于spr…...
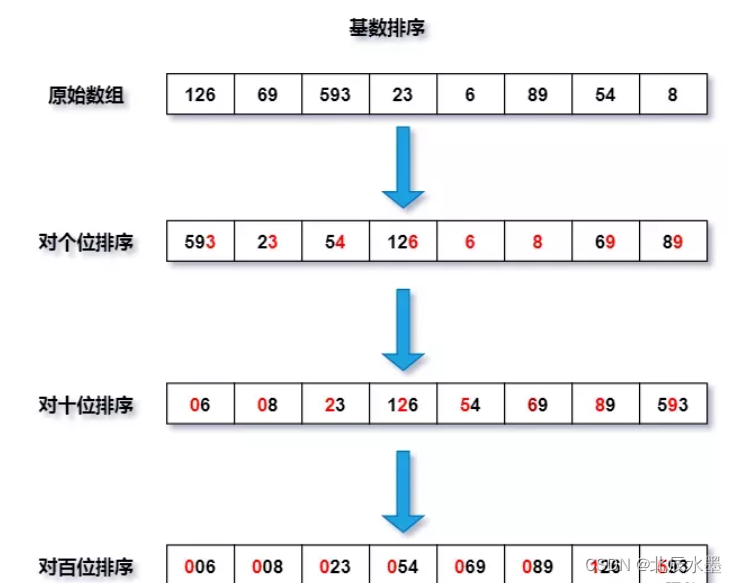
十大排序算法(冒泡排序、插入排序、选择排序、希尔排序、堆排序、快排、归并排序、桶排序、计数排序、基数排序)
目录 一、冒泡排序: 二、插入排序: 三、选择排序: 四、希尔排序: 五、堆排序: 六、快速排序: 6.1挖坑法: 6.2左右指针法 6.3前后指针法: 七、归并排序: 八、桶…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
