Python网站的搭建和html基础
1.Python网站代码及讲解
一般我们搭建小型的网站就用flask库就行了。
（1）安装flask库
安装完python后，按住windows徽标键和r,弹出“运行”，在里面输入cmd。
回车打开，输入“pip install flask”。
（2）代码
新建一个python文件，命名为app.py。
Python：
from flask import Flask, render_templateapp = Flask(__name__)@app.route('/')
def hello_world():return render_template('start.html')if __name__=="__main__":app.run(host='0.0.0.0')在和app.py同一目录中，创建一个文件夹，命名为templates，我们把html文件放在这里。
在templates文件夹中创建一个文件，这里和上面的代码呼应，就命名为start.html。
我们在start.html中输入如下代码：
html:
<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title>我的第一个网站</title>
</head>
<body><h1>Hello world!</h1>
</body>
</html>最后，我们运行一下代码，如下图：
点击http://127.0.0.1:5000。效果如下图：
2.注意事项
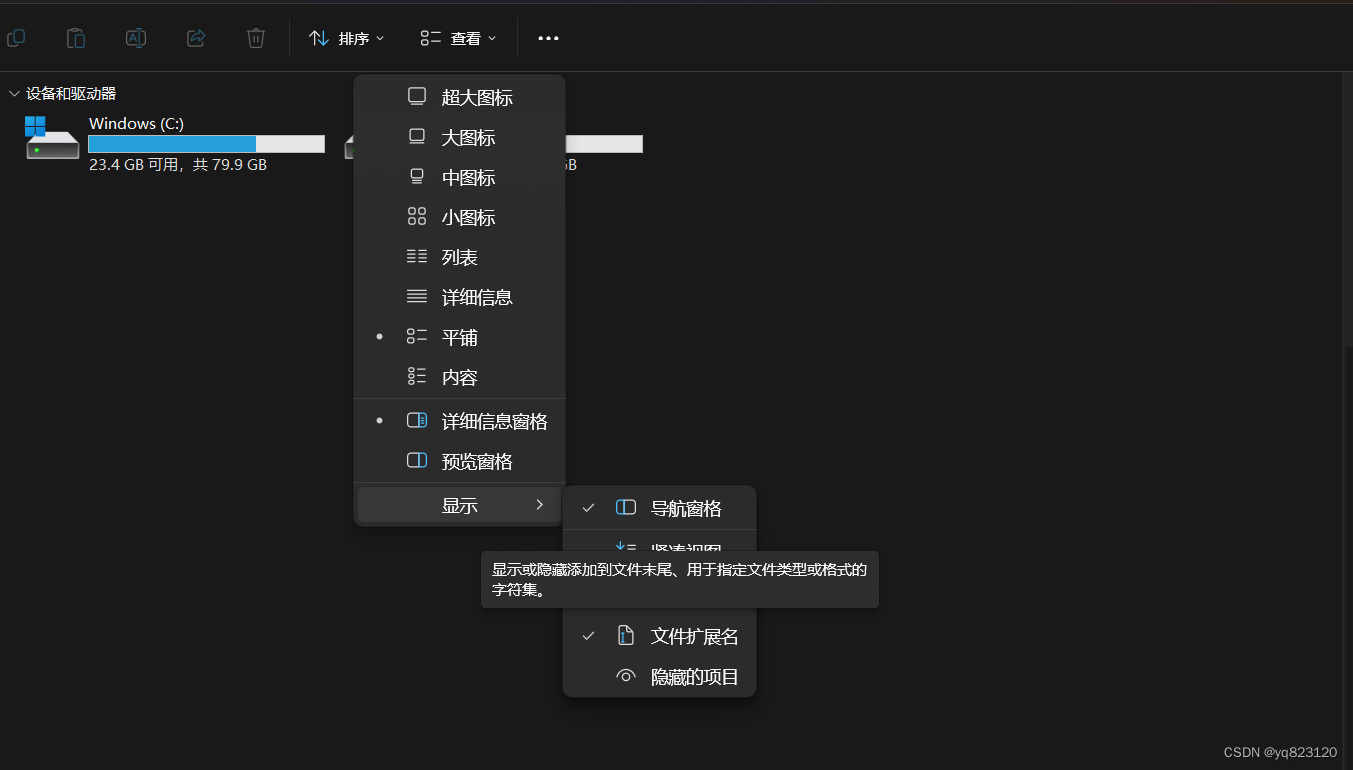
注意：一定要开启文件后缀名，如下图所示。
笔者所用的是windows11的版本。
3.PyCharm的安装和汉化
（1）安装
这里，笔者所用的Python IDLE为PyCharm，PyCharm：JetBrains为专业开发者提供的Python IDE. Python与Django IDE，支持智能代码补全、实时错误检查和快速修复，还支持HTML和CSS等等……
链接：下载 JetBrains 提供的 PyCharm：用于数据科学和 Web 开发的 Python IDE
https://www.jetbrains.com/pycharm/download/?section=windows
注意：没有特殊需要的读者，可以下载免费的社区版PyCharm。如下图所示：
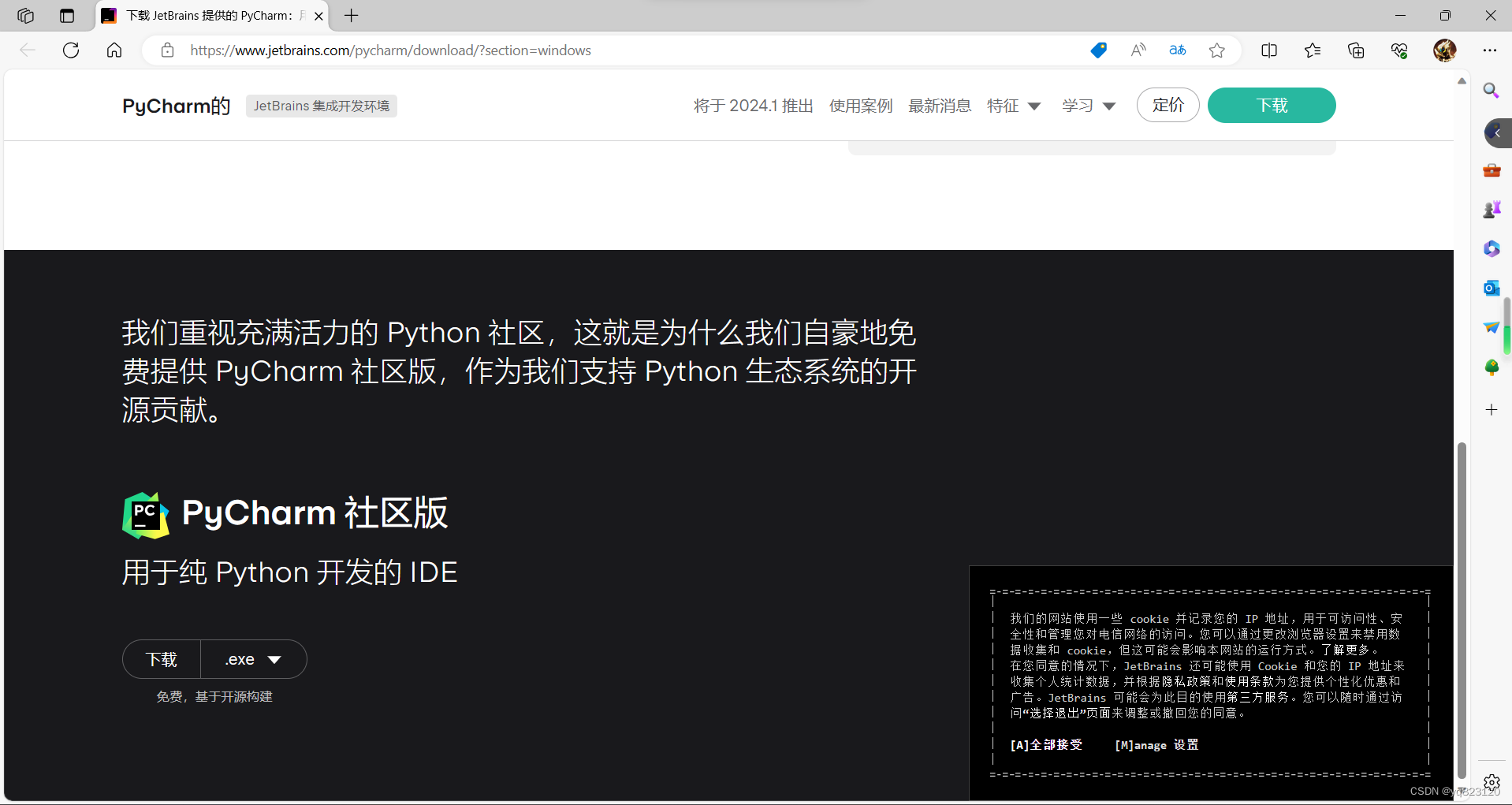（2）汉化
第一步，打开PyCharm，打开设置。
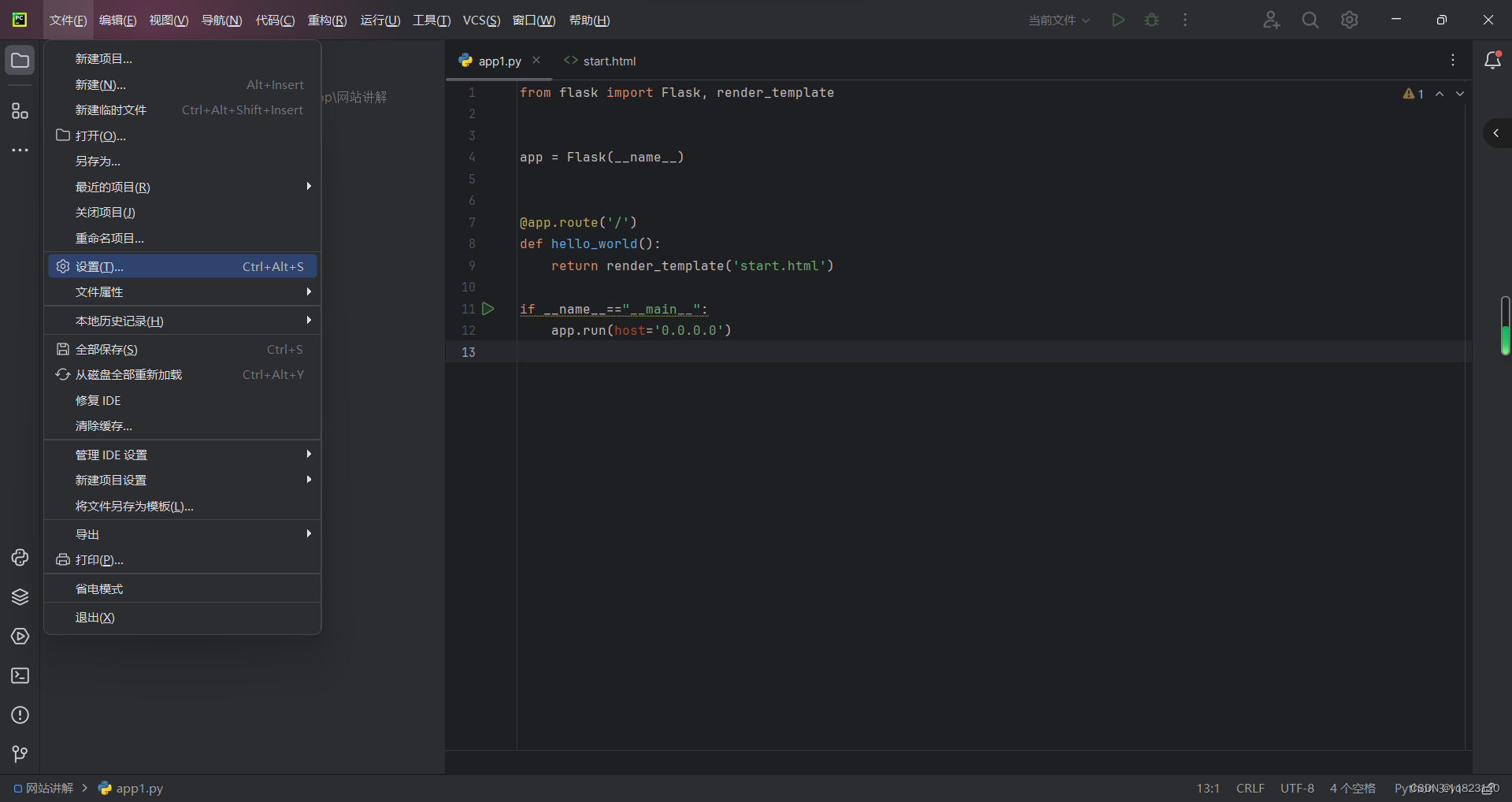
在设置中代开插件，搜索Chinese Language Pack。
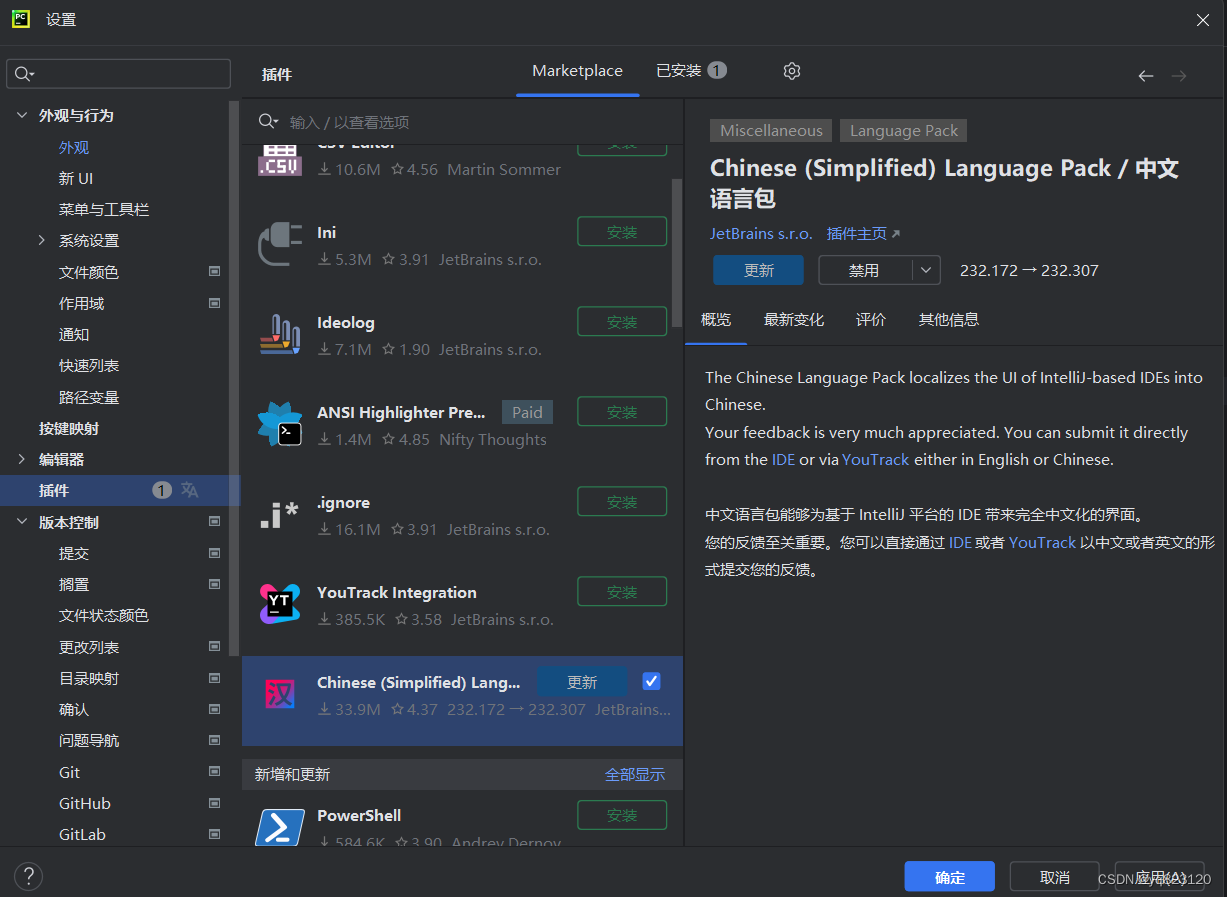
安装完后重启程序，就可以体验全中文的PyCharm了。
4.Python IDLE的安装
因为PyCharm运行程序是基于Python IDLE的，所以我们还要安装Python IDLE。
链接：
欢迎来到 Python.orghttps://www.python.org/安装后，打开Python IDLE，如下图：
完结撒花*★,°*:.☆(￣▽￣)/$:*.°★* 。
下一篇文章，笔者会详细讲解html的语法。
相关文章：
Python网站的搭建和html基础
1.Python网站代码及讲解 一般我们搭建小型的网站就用flask库就行了。 （1）安装flask库 安装完python后，按住windows徽标键和r,弹出“运行”，在里面输入cmd。 回车打开，输入“pip install flask”。 （2&am…...
SpringCloud(21)之SpringCloud Alibaba Nacos实战应用
一、Nacos安装 1.1 Nacos概述 Nacos是Alibaba微服务生态组件中的重要组件之一，主要用它实现应用的动态服务发现、配置管理、 服务管理。Nacos discovery alibaba/spring-cloud-alibaba Wiki GitHub Nacos 致力于帮助您发现、配置和管理微服务。Nacos 提供了一组简…...
Python 基础语法：基本数据类型（元组）
1 元组（Tuples）概述 1.1 元组的定义与特点 元组（Tuples）是Python中的一个内置数据类型，用于存储一系列有序的元素。元组中的元素可以是任何类型，包括数字、字符串、列表等，且元素之间用逗号…...
vuepress-theme-vdoing博客搭建教程
搭建流程 前言 这是笔者搭建个人博客所经历的流程，特附上笔记 笔者个人博客地址：沉梦听雨的编程指南 一、主题介绍 本博客使用的主题为：vuepress-theme-vdoing，相关介绍和使用方法可以参考该主题的官方文档 官方文档快速上手…...
ICC2：create terminal参考脚本
我正在「拾陆楼」和朋友们讨论有趣的话题，你⼀起来吧？ 拾陆楼知识星球入口 set list "" set i 0 ; set length xx set width xx foreach port $list { if {$i ＝＝ 0} { set startx 0 set starty 0 } else { set sta…...
并行计算CUDA DEMO
//并行计算CUDA DEMO #include "cuda_runtime.h" #include "device_launch_parameters.h" #include <stdio.h> cudaError_t addWithCuda(int *c, const int *a, const int *b, unsigned int size); __global__ void addKernel(int *c, const int …...
【linux线程(一)】什么是线程?怎样操作线程?
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:Linux从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学更多操作系统知识 🔝🔝 Linux线程 1. 前言2. 什么是线…...
python-0002-linux安装pycharm
下载软件包 下载地址：https://download.csdn.net/download/qq_41833259/88944791 安装 # 解压 tar -zxvf 你的软件包 # 进入软件解压后的路径，如解压到了/home/soft/pycharm cd /home/soft/pycharm cd bin # 执行启动命令 sh pycharm.sh # 等待软件启…...
扭蛋机小程序，扭蛋与互联网结合下的商机
扭蛋机作为一种娱乐消费模式，受众群体不再局限于儿童，也吸引了众多的年轻消费者。扭蛋机具有较大的随机性，玩具商品随机掉落，在购买前消费者完全不知道扭蛋中的商品是什么，这种未知性带来的惊喜感是吸引众多消费者的主…...
pytorch CV入门3-预训练模型与迁移学习
专栏链接：https://blog.csdn.net/qq_33345365/category_12578430.html 初次编辑：2024/3/7；最后编辑：2024/3/8 参考网站-微软教程：https://learn.microsoft.com/en-us/training/modules/intro-computer-vision-pytorc…...
Swift SwiftUI 学习笔记 2024
Swift SwiftUI 学习笔记 2024 一、资源 视频资源 StanfordUnivercity 公开课 2023: https://cs193p.sites.stanford.edu/2023 教程 Swift 初识：基础语法：https://docs.swift.org/swift-book/documentation/the-swift-programming-language/guidedtour/…...
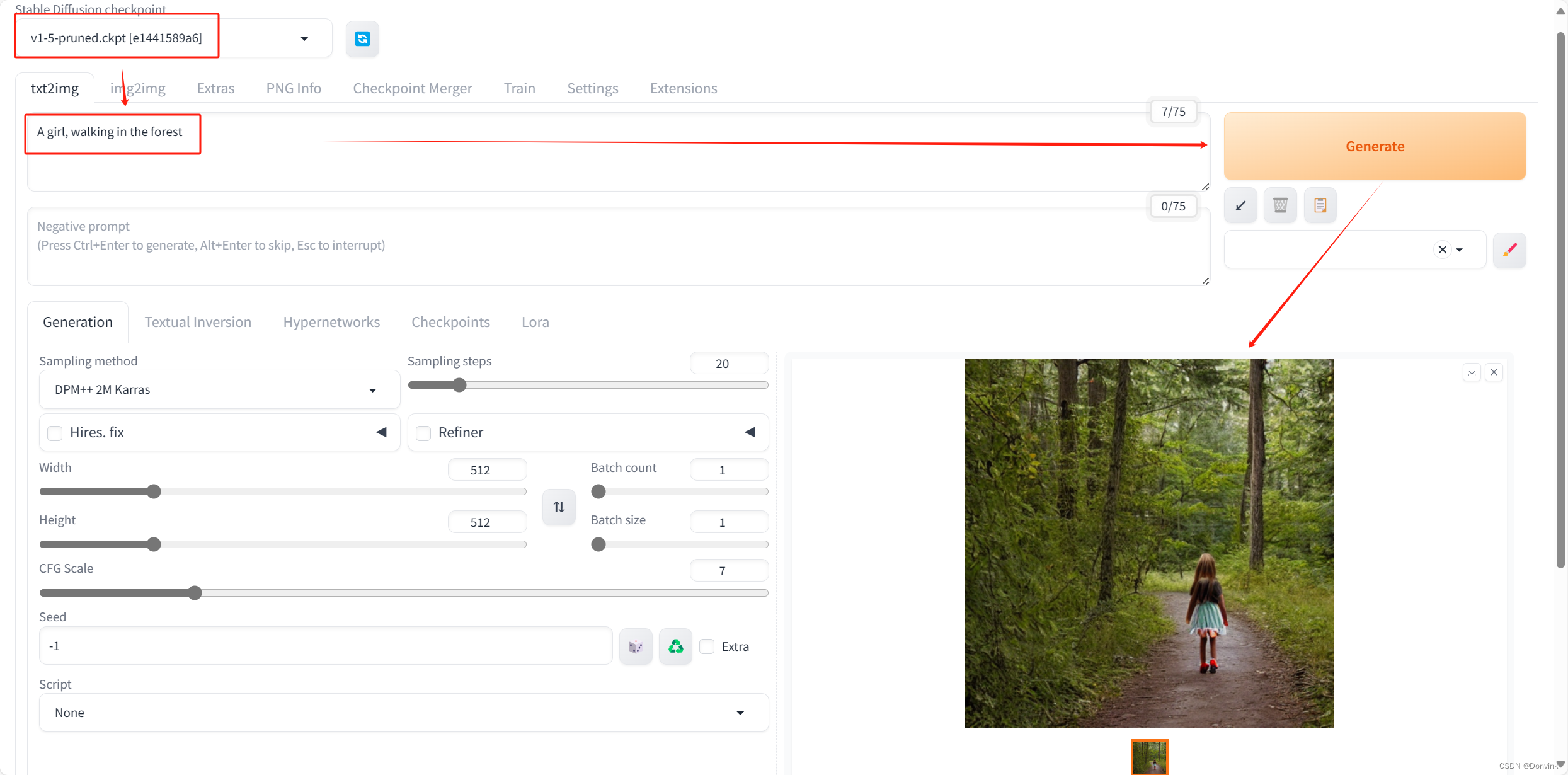
【Stable Diffusion】入门：原理简介+应用安装（Windows）+生成步骤
【Stable Diffusion】入门：原理简介应用安装（Windows）生成步骤 原理简介应用安装 原理简介 稳定扩散生成模型(Stable Diffusion)是一种潜在的文本到图像扩散模型，能够在给定任何文本输入的情况下生成照片般逼真的图像。 应用安…...
【栈】第十二届蓝桥杯省赛第一场C++ B组/研究生组《双向排序》（c++）
【题目描述】 给定序列 (a1,a2,⋅⋅⋅,an)(1,2,⋅⋅⋅,n)，即 aii。 小蓝将对这个序列进行 m 次操作，每次可能是将 a1,a2,⋅⋅⋅,aqi 降序排列，或者将 aqi,aqi1,⋅⋅⋅,an 升序排列。 请求出操作完成后的序列。 【输入格式】 输入的第一行…...
Gitea 安装和配置
Gitea 安装和配置: http://coffeelatte.vip.cpolar.top/post/software/applications/gitea/gitea_安装和配置/ 文章目录 Gitea 安装和配置: <http://coffeelatte.vip.cpolar.top/post/software/applications/gitea/gitea_%E5%AE%89%E8%A3%85%E5%92%8C%E9%85%8D%E7%BD%AE/>…...
CEF JS与c++能够交互的原理 以及 JS 调用C++的流程分析
相关章节：CEF 之 Render进程 与 Browser进程通信 目录 一、JS与c++能够交互的原理 二、JS调用C++ 流程梳理...
关于比特币的AI对话
【ChatGPT】 比特币源码开源吗？ 是的，比特币的源码是开源的。比特币项目是在MIT许可证下发布的，这意味着任何人都可以查看、修改、贡献和分发代码。比特币的源码托管在GitHub上，可以通过下面的链接进行访问： https://g…...
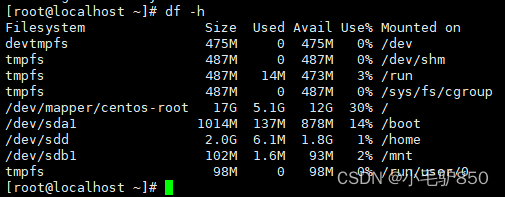
Linux查看磁盘命令df-h详解
df -h 是一个常用的 Linux 命令，用于查看文件系统的磁盘使用情况并以易于阅读的方式显示。以下是 df -h 命令的详细解释： -h：以人类可读的格式显示磁盘空间大小。例如，使用 GB、MB、KB 等单位代替字节。 执行 df -h 命令后&…...
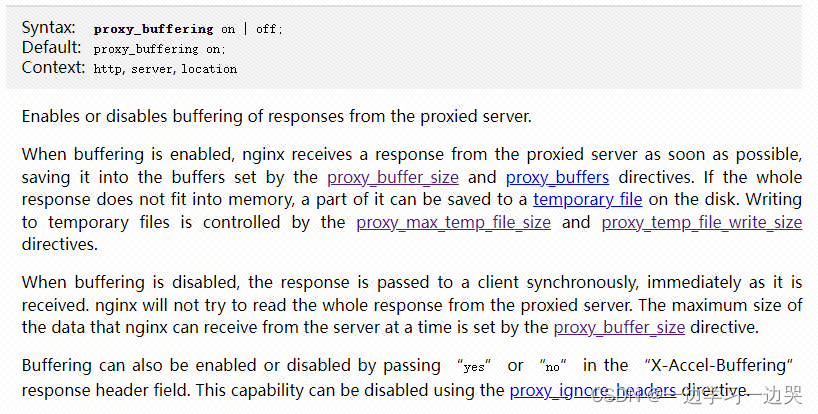
nginx-排查一次大文件无法正常下载问题
目录 问题现象&报错信息 问题现象以及分析 nginx报错信息 问题解决 方法1：配置proxy_max_temp_file_size 方法2：关闭proxy_buffering 参考文档 问题现象&报错信息 问题现象以及分析 文件正常从后端服务器直接下载时，一切正常…...
基于yolov5的草莓成熟度检测系统，可进行图像目标检测，也可进行视屏和摄像检测（pytorch框架）【python源码+UI界面+功能源码详解】
功能演示： 基于yolov5的草莓成熟度检测系统，系统既能够实现图像检测，也可以进行视屏和摄像实时检测_哔哩哔哩_bilibili （一）简介 基于yolov5的草莓成熟度系统是在pytorch框架下实现的，这是一个完整的项目…...
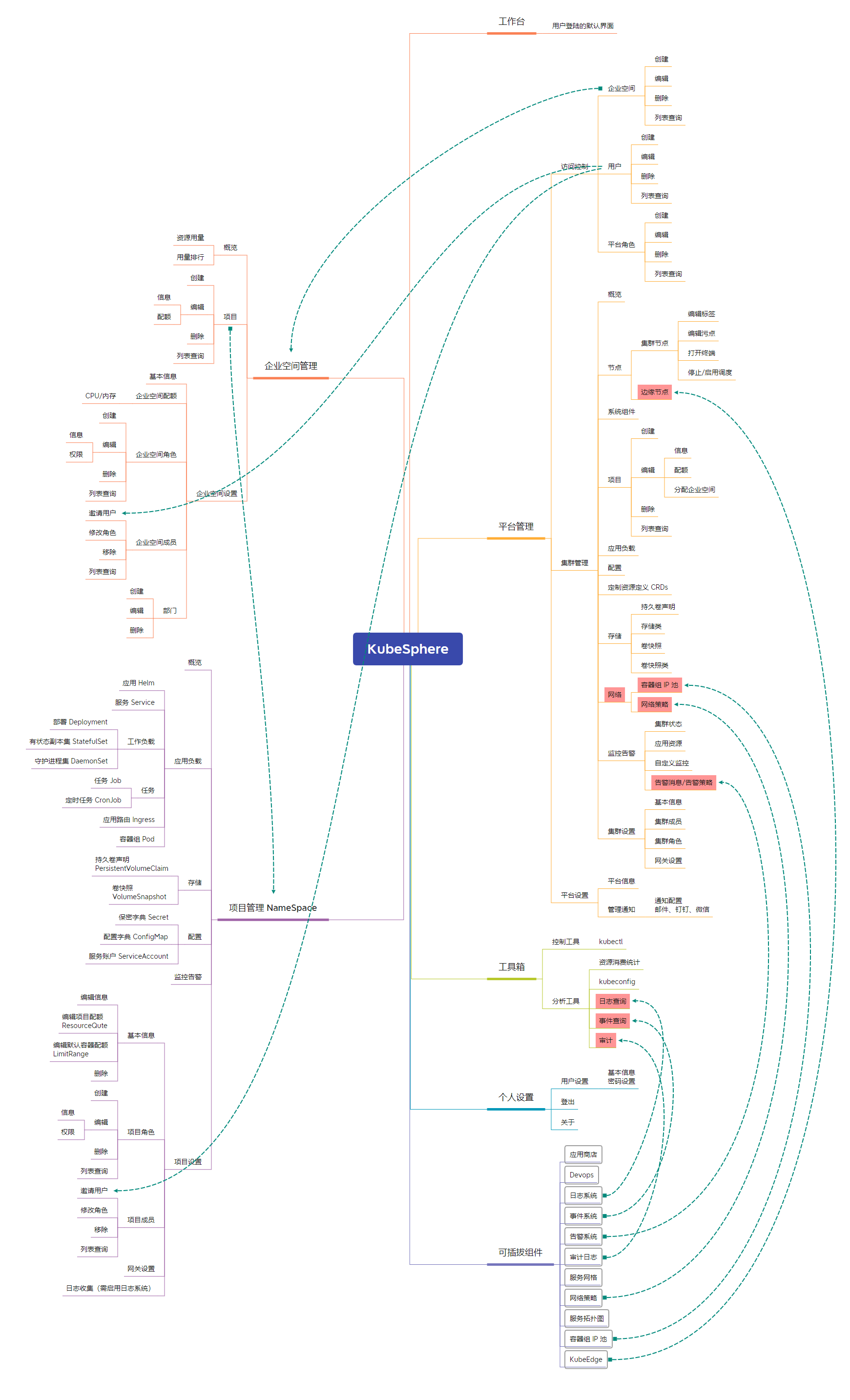
Kubesphere 保姆级分析
应用场景 KubeSphere 适用于多种场景，为企业提供容器化的环境，借助完善的管理和运维功能，让企业在数字化转型过程中从容应对各种挑战和各类业务场景，如多云多集群管理、敏捷软件开发、自动化运维、微服务治理、流量管理以及 DevO…...
渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义，在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容，其实不管是方块还是方块实体，都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器，用于动态创…...
《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术，说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号（调制） 把信息从信号中抽取出来&am…...
令牌桶 滑动窗口-＞限流 分布式信号量-＞限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结： 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析： 实际业务去理解体会统一注…...
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码： prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
【HTTP三个基础问题】
面试官您好！HTTP是超文本传输协议，是互联网上客户端和服务器之间传输超文本数据（比如文字、图片、音频、视频等）的核心协议，当前互联网应用最广泛的版本是HTTP1.1，它基于经典的C/S模型，也就是客…...
什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具，可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板，允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板，并通…...
laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...
回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
解决：Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象： android studio报错： [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决： 不要动CMakeLists.…...
【Linux系统】Linux环境变量：系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量：setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...