扭蛋机小程序,扭蛋与互联网结合下的商机
扭蛋机作为一种娱乐消费模式,受众群体不再局限于儿童,也吸引了众多的年轻消费者。扭蛋机具有较大的随机性,玩具商品随机掉落,在购买前消费者完全不知道扭蛋中的商品是什么,这种未知性带来的惊喜感是吸引众多消费者的主要原因。
目前,动漫产业发展非常迅速,这为扭蛋机行业提供了很大的市场需求,也为扭蛋商品提供了源源不断的商机。
扭蛋机在发展中,除了确保商品的创新,扭蛋机的玩法和新奇度也是企业获得盈利的关键。在当下信息化时代,扭蛋机的发展也需要顺应时代,向数字化发展,让玩家体验到线上扭蛋机带来的乐趣,推动扭蛋机市场的快速发展。

线上扭蛋机能够给玩家带来新鲜感,它可以根据节日进行主题更换,不在局限于单一主题。其次,线上玩法较多,抽奖、互动等功能都较为齐全,满足了玩家不断上升的需求。
扭蛋机小程序功能特点
1、操作简单
玩家在小程序上能够简单操作,直接选择扭蛋机进行扭蛋,商品会随机出来。玩家还可以随时随地进行体验,不受限制,大大提高了玩家的扭蛋体验。小程序也能够自动上下架商品,能够降低服务商的人力物力。
2、商品丰富
小程序中的扭蛋商品种类比较齐全,奖品也不再单一,涵盖了市面上的大部分热门赏品和隐藏款。小程序还可以定期推动各种扭蛋主题活动,增加用户的体验。
3、玩法丰富
小程序的玩法可以任意设置,满足当下玩家对玩法的要求。玩家还可以用积分兑换抽奖次数,获得隐藏款商品。
4、数据透明
小程序上的信息都是公开透明的,用户可以看到扭蛋商品信息、积分信息,以及中奖商品的快递信息。
5、数据分析
小程序后台可以实时更新数据,方便服务商浏览,及时调整服务方向以及营销策略,增加用户的黏性。
相关文章:

扭蛋机小程序,扭蛋与互联网结合下的商机
扭蛋机作为一种娱乐消费模式,受众群体不再局限于儿童,也吸引了众多的年轻消费者。扭蛋机具有较大的随机性,玩具商品随机掉落,在购买前消费者完全不知道扭蛋中的商品是什么,这种未知性带来的惊喜感是吸引众多消费者的主…...

pytorch CV入门3-预训练模型与迁移学习
专栏链接:https://blog.csdn.net/qq_33345365/category_12578430.html 初次编辑:2024/3/7;最后编辑:2024/3/8 参考网站-微软教程:https://learn.microsoft.com/en-us/training/modules/intro-computer-vision-pytorc…...

Swift SwiftUI 学习笔记 2024
Swift SwiftUI 学习笔记 2024 一、资源 视频资源 StanfordUnivercity 公开课 2023: https://cs193p.sites.stanford.edu/2023 教程 Swift 初识:基础语法:https://docs.swift.org/swift-book/documentation/the-swift-programming-language/guidedtour/…...
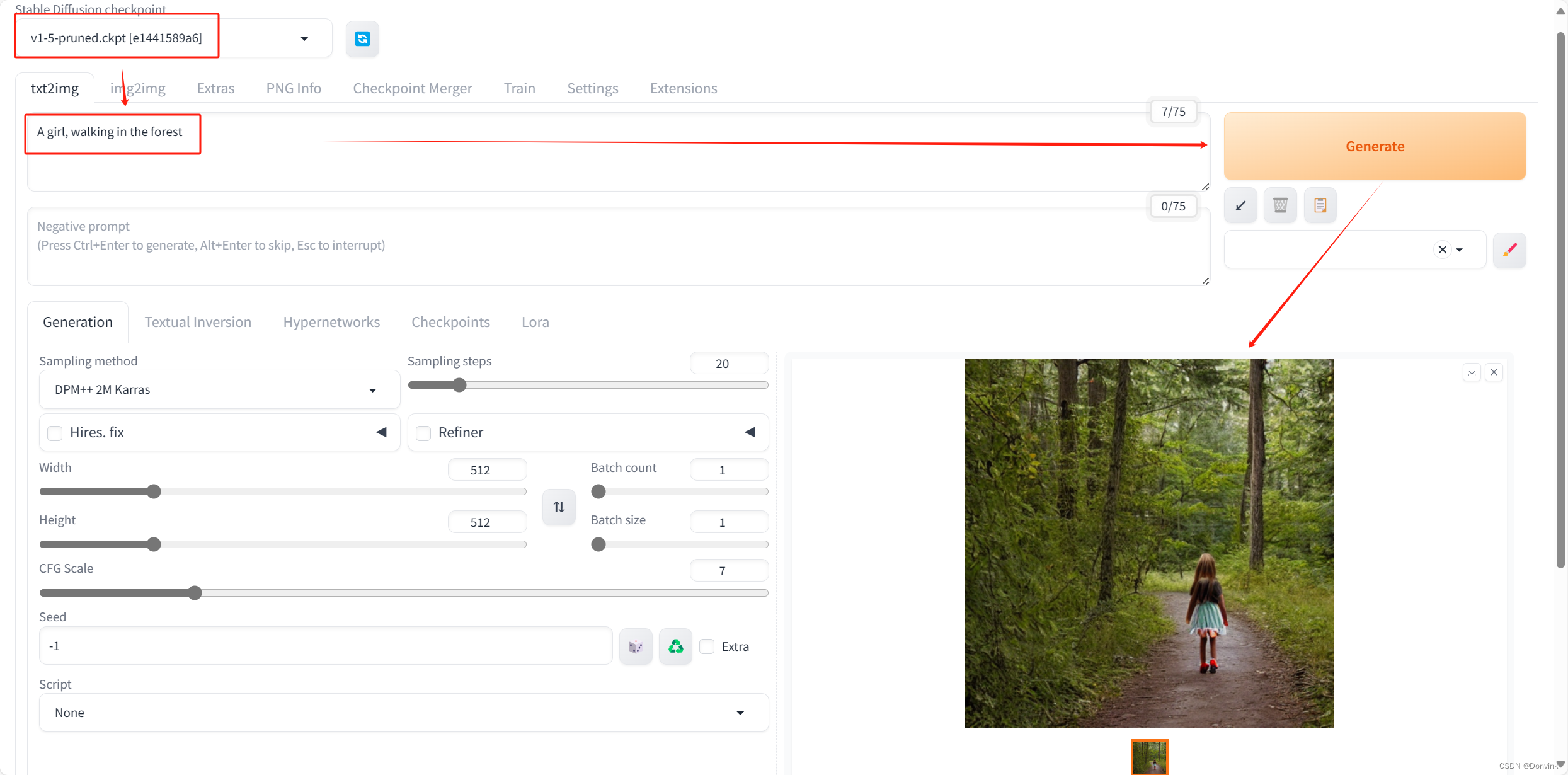
【Stable Diffusion】入门:原理简介+应用安装(Windows)+生成步骤
【Stable Diffusion】入门:原理简介应用安装(Windows)生成步骤 原理简介应用安装 原理简介 稳定扩散生成模型(Stable Diffusion)是一种潜在的文本到图像扩散模型,能够在给定任何文本输入的情况下生成照片般逼真的图像。 应用安…...
)
【栈】第十二届蓝桥杯省赛第一场C++ B组/研究生组《双向排序》(c++)
【题目描述】 给定序列 (a1,a2,⋅⋅⋅,an)(1,2,⋅⋅⋅,n),即 aii。 小蓝将对这个序列进行 m 次操作,每次可能是将 a1,a2,⋅⋅⋅,aqi 降序排列,或者将 aqi,aqi1,⋅⋅⋅,an 升序排列。 请求出操作完成后的序列。 【输入格式】 输入的第一行…...

Gitea 安装和配置
Gitea 安装和配置: http://coffeelatte.vip.cpolar.top/post/software/applications/gitea/gitea_安装和配置/ 文章目录 Gitea 安装和配置: <http://coffeelatte.vip.cpolar.top/post/software/applications/gitea/gitea_%E5%AE%89%E8%A3%85%E5%92%8C%E9%85%8D%E7%BD%AE/>…...

CEF JS与c++能够交互的原理 以及 JS 调用C++的流程分析
相关章节:CEF 之 Render进程 与 Browser进程通信 目录 一、JS与c++能够交互的原理 二、JS调用C++ 流程梳理...

关于比特币的AI对话
【ChatGPT】 比特币源码开源吗? 是的,比特币的源码是开源的。比特币项目是在MIT许可证下发布的,这意味着任何人都可以查看、修改、贡献和分发代码。比特币的源码托管在GitHub上,可以通过下面的链接进行访问: https://g…...
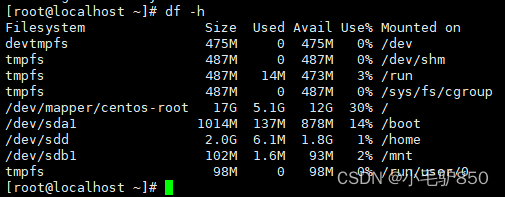
Linux查看磁盘命令df-h详解
df -h 是一个常用的 Linux 命令,用于查看文件系统的磁盘使用情况并以易于阅读的方式显示。以下是 df -h 命令的详细解释: -h:以人类可读的格式显示磁盘空间大小。例如,使用 GB、MB、KB 等单位代替字节。 执行 df -h 命令后&…...
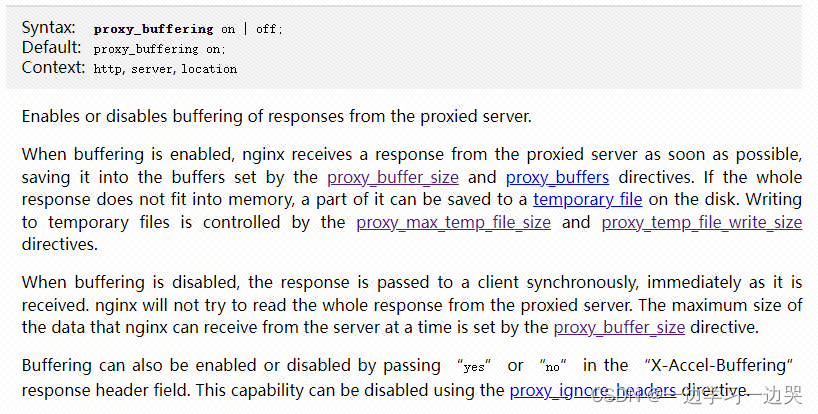
nginx-排查一次大文件无法正常下载问题
目录 问题现象&报错信息 问题现象以及分析 nginx报错信息 问题解决 方法1:配置proxy_max_temp_file_size 方法2:关闭proxy_buffering 参考文档 问题现象&报错信息 问题现象以及分析 文件正常从后端服务器直接下载时,一切正常…...

基于yolov5的草莓成熟度检测系统,可进行图像目标检测,也可进行视屏和摄像检测(pytorch框架)【python源码+UI界面+功能源码详解】
功能演示: 基于yolov5的草莓成熟度检测系统,系统既能够实现图像检测,也可以进行视屏和摄像实时检测_哔哩哔哩_bilibili (一)简介 基于yolov5的草莓成熟度系统是在pytorch框架下实现的,这是一个完整的项目…...
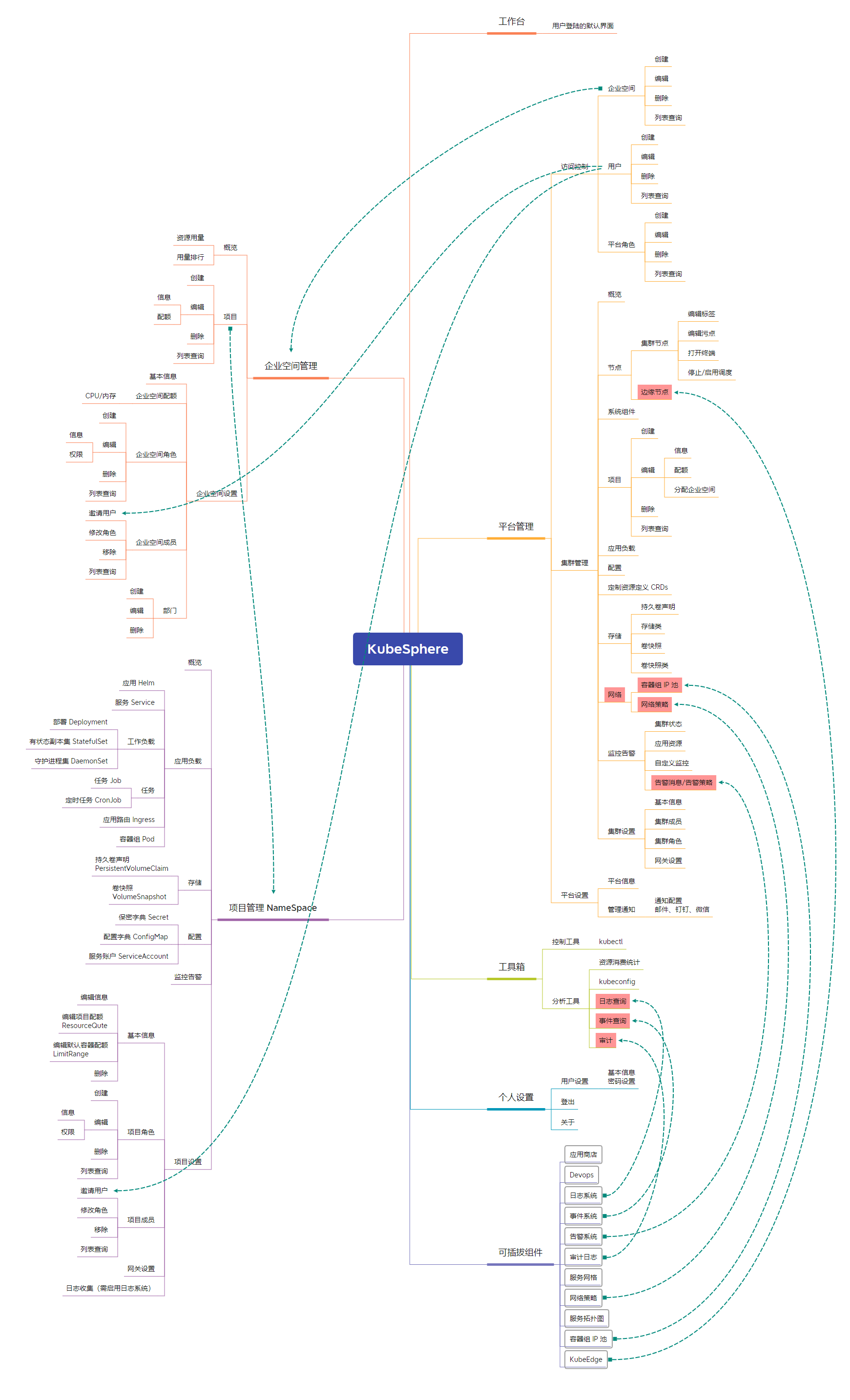
Kubesphere 保姆级分析
应用场景 KubeSphere 适用于多种场景,为企业提供容器化的环境,借助完善的管理和运维功能,让企业在数字化转型过程中从容应对各种挑战和各类业务场景,如多云多集群管理、敏捷软件开发、自动化运维、微服务治理、流量管理以及 DevO…...

力扣hot100:240.搜索二维矩阵II(脑子)
吉大21级算法分析与设计的一道大题,由于每一行都是排好序的直接逐行二分 可以达到:O(mlogn)。但是这里追求更广的思路可以使用其他方法。 矩阵四分: 在矩阵中用中心点比较,如果target大于中心点的值,则由于升序排列&am…...
)
Apache Hive(三)
一、Apache Hive 1、ETL数据清洗 数据问题 问题1:当前数据中,有一些数据的字段为空,不是合法数据 解决:where 过滤 问题2:需求中,需要统计每天、每个小时的消息量,但是数据中没有天和小时字段…...
的概念,并说明在Python中如何使用)
ORM(对象关系映射)的概念,并说明在Python中如何使用
ORM(对象关系映射)的概念,并说明在Python中如何使用 ORM(对象关系映射)是一种编程技术,它实现了将关系型数据库中的数据映射到程序中的对象模型,使得开发者能够使用面向对象的方式来操作数据…...

Br 算法
基于google的brotli开源,实现Br算法。 #include <brotli/encode.h> #include <brotli/decode.h>namespace br {/*compress unsigned char* content,if ok return non empty unsigned char * */std::string compress_string(const std::string& c…...

GPT实战系列-一种构建LangChain自定义Tool工具的简单方法
GPT实战系列-一种构建LangChain自定义Tool工具的简单方法 LLM大模型: GPT实战系列-探究GPT等大模型的文本生成 GPT实战系列-Baichuan2等大模型的计算精度与量化 GPT实战系列-GPT训练的Pretraining,SFT,Reward Modeling,RLHF …...

【Docker】Memcached 容器化部署
Memcached环境标准软件基于Bitnami Memcached 构建。当前版本为1.6.24 你可以通过轻云UC部署工具直接安装部署,也可以手动按如下文档操作,该项目已经全面开源,可以从如下环境获取 配置文件地址: https://gitee.com/qingplus/qingcloud-platf…...

Langchain-Chatchat本地搭建ChatGLM3模型和提取PDF内容
文章目录 1、软件要求2、安装CUDA2.1、安装gcc2.2、安装CUDA 3、安装Anaconda33.1、下载Anaconda33.2、创建python虚拟环境 4、部署系统4.1、下载源码4.2、安装依赖4.3、下载模型4.4、初始化配置和知识库4.4.1、初始化配置4.4.2、初始化知识库 4.5、运行4.6、运行4.6.1、启动4.…...
案例分析篇03:一篇文章搞定软考设计模式考点(2024年软考高级系统架构设计师冲刺知识点总结系列文章)
专栏系列文章推荐: 2024高级系统架构设计师备考资料(高频考点&真题&经验)https://blog.csdn.net/seeker1994/category_12593400.html 【历年案例分析真题考点汇总】与【专栏文章案例分析高频考点目录】(2024年软考高级系统架构设计师冲刺知识点总结-案例分析篇-…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...
