常见排序算法(C++)
评判一个排序算法时除了时间复杂度和空间复杂度之外还要考虑对cache的捕获效果如何,cache友好的排序算法应该对数据的访问相对集中,快速排序相较于堆排序优点就是在于对cache的捕获效果好。
堆排序
时间复杂度:O(n log n )
空间复杂度 O(1) 不稳定
cache不友好
void func(vector<int>&nums){function<void(int,int)>merge=[&](int start,int end){int child=start;int father=2*child+1;while(child<=end){if(child+1<=end&&nums[child+1]>nums[child]) child++;if(nums[father]<nums[child]){swap(nums[father],nums[child]);child=father;father=2*child+1;}else break;}};int n=nums.size();for(int i=n/2-1;i>=0;i--){merge(i,n-1);}for(int i=n-1;i>=0;i--){swap(nums[0],nums[i]);merge(0,i-1);}
}
快速排序
时间复杂度O(n log n)- O(n^2)
空间复杂度 O(1)
cache友好
void func(vector<int>&nums,int start,int end){if(start>=end) return;int s=start-1;int e=end+1;int val=nums[start];//这里选值可以优化int index=start;while(index<e){if(nums[index]==val) {index++;}else if(nums[index]<val){swap(nums[index],nums[++s]);index++;}else swap(nums[index],nums[--e]);}func(nums,start,s);func(nums,e,end);
}
归并排序
时间复杂度 O(n log n)
空间复杂度 O(n)
cache友好
void func(vector<int>&nums,int start,int end){if(start>=end) return;int mid=(start+end)/2;func(nums,start,mid);func(nums,mid+1,end);vector<int>tmp(end-start+1);int start1=start,start2=mid+1;int index=0;while(start1<=mid&&start2<=end){int val1=start1<=mid?nums[start1]:INT_MAX;int val2=start2<=end?nums[start2]:INT_MAX;if(val1>val2) tmp[index++]=nums[start2++];else tmp[index++]=nums[start1++];}for(int i=start;i<=end;i++) nums[i]=nums[i-start];
}
选择排序
时间复杂度 O(n^2)
空间复杂度 O(1)
cache不友好
void func(vector<int>&nums){int n=nums.size();for(int i=1;i<n;i++){int index=0;for(int j=0;j<n-i;j++){if(nums[index]>nums[j]) index=j;}swap(nums[index],nums[n-i]);}
}
插入排序
时间复杂度 O(n^2)
空间复杂度 O(1)
cache友好
void func(vector<int>&nums){int n=nums.size();for(int i=1;i<n;i++){int val=nums[i],j=i-1;while(j>=0&&nums[j]>val){nums[j+1]=nums[j--];}nums[j+1]=val;}
}
冒泡排序
时间复杂度 O(n^2)
空间复杂度 O(1)
cache不友好
void func(vector<int>&nums){int n=nums.size();for(int i=0;i<n;i++){bool b=true;for(int j=i+1;j<n;j++){if(nums[i]>nums[j]) {b=false;swap(nums[i],nums[j]);}}if(b) break;}
}
相关文章:
)
常见排序算法(C++)
评判一个排序算法时除了时间复杂度和空间复杂度之外还要考虑对cache的捕获效果如何,cache友好的排序算法应该对数据的访问相对集中,快速排序相较于堆排序优点就是在于对cache的捕获效果好。 堆排序 时间复杂度:O(n log n …...

多线程编程互斥锁mutex的创建
在Linux下的多线程编程中,互斥锁(mutex)的创建主要有两种方式:静态分配和动态分配。这两种方式的主要区别在于互斥锁的生命周期和初始化方式。 静态分配(静态方式) 静态分配方式是在程序编译时就已经确定互…...

在 SpringBoot3 中使用 Mybatis-Plus 报错
在 SpringBoot3 中使用 Mybatis-Plus 报错 Property ‘sqlSessionFactory’ or ‘sqlSessionTemplate’ are required Caused by: java.lang.IllegalArgumentException: Property sqlSessionFactory or sqlSessionTemplate are requiredat org.springframework.util.Assert.no…...
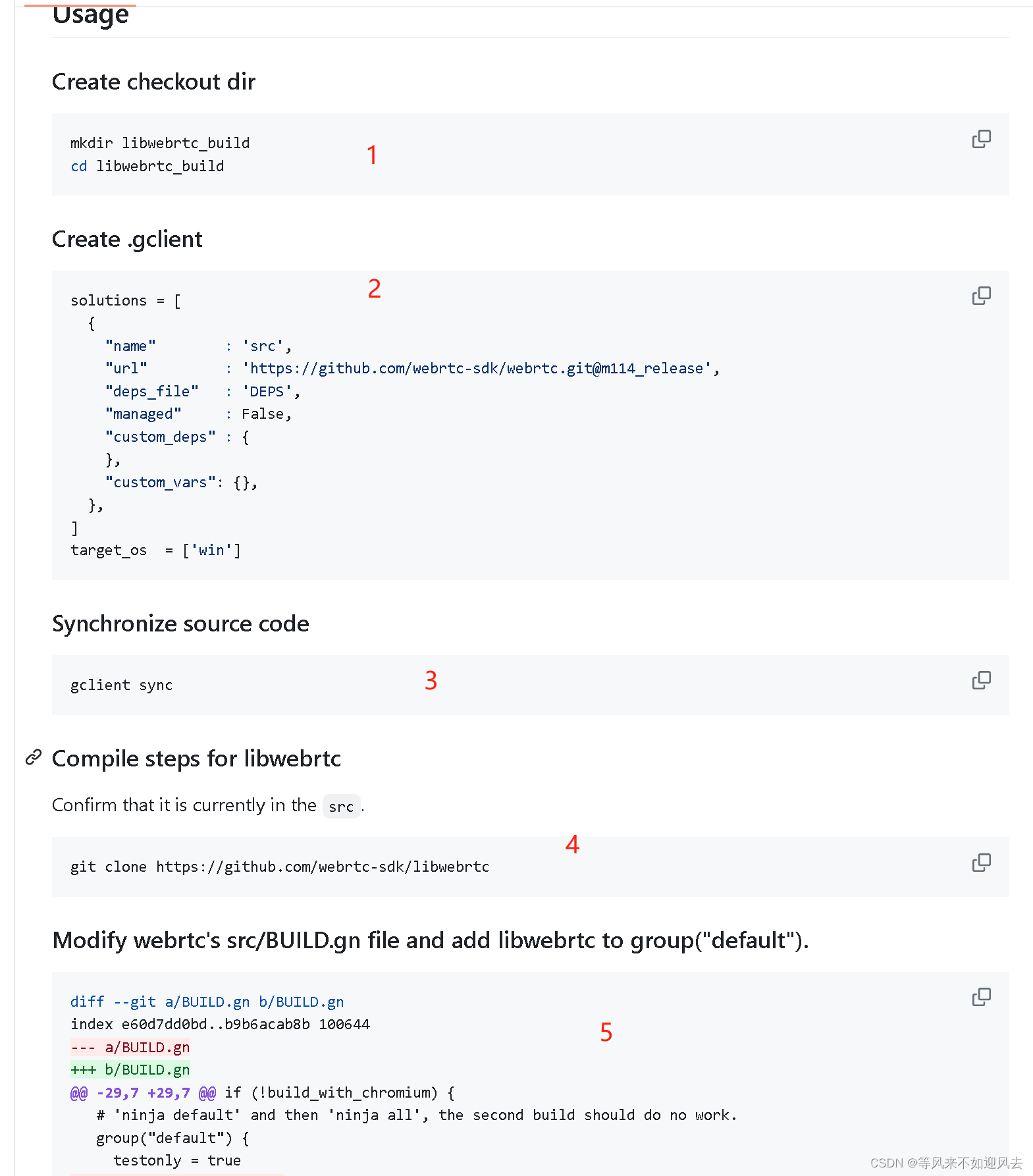
【libwebrtc】基于m114的构建
libwebrtc A C++ wrapper for binary release, mainly used for flutter-webrtc desktop (windows, linux, embedded).是 基于m114版本的webrtc 最新(20240309 ) 的是m122了。官方给出的构建过程 .gclient 文件 solutions = [{"name" : src,"url...
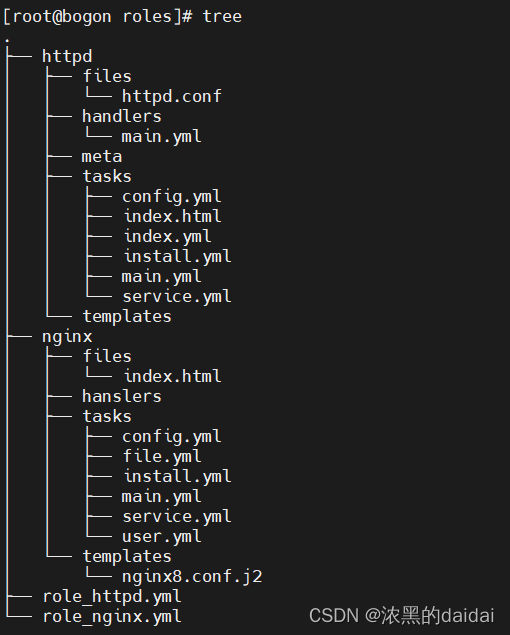
ansible-playbook的角色(role)
1前言 角色目录如下(分别为httpd角色和nginx角色) handlers/ :至少应该包含一个名为 main.yml 的文件; 其它的文件需要在此文件中通过include 进行包含 vars/ :定义变量,至少应该包含一个名为 main.yml 的…...
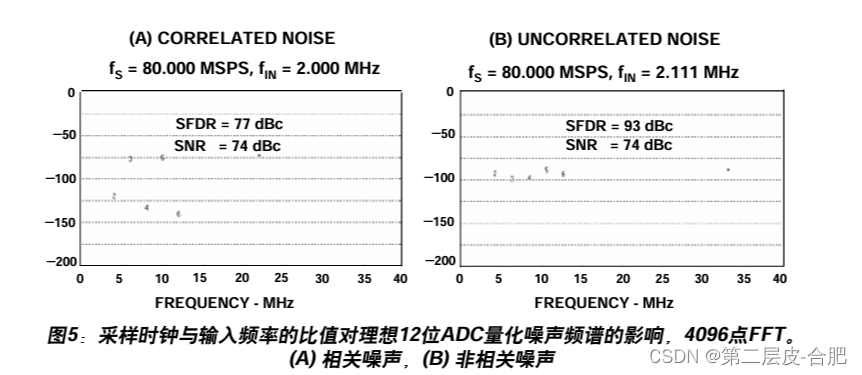
SNR = 6.02N + 1.76dB 公式推导
简介 接触ADC或DAC时您一定会碰到这个经常被引用的公式,用于计算转换器理论信噪比 (SNR)。与其盲目地相信表象,不如从根本上了解其来源,因为该公式蕴含着一些微妙之 处,如果不深入探究,可能导致对数据手册技术规格和转…...

归并排序 刷题笔记
归并排序的写法 归并排序 分治双指针 1.定义一个mid if(l>r)return ; 2.分治 sort(q,l,mid); sort(q,mid1,r); 3. 双指针 int il,jmid,k0; 将双序列扫入 缓存数组 条件 while(i<mid&&j<r) 两个数列比较大小 小的一方 进入缓存数组 4. 扫尾 while(…...

字节一面:TCP 和 UDP 可以使用同一个端口吗?
数据包是计算机网络通信的核心,包含头部和数据负载。TCP和UDP协议在传输层使用端口号区分服务和应用。操作系统通过IP头部中的协议字段和端口号来管理网络流量,确保TCP和UDP流量即使共用端口号也不会相互干扰。 在现代计算机网络中,数据传输…...
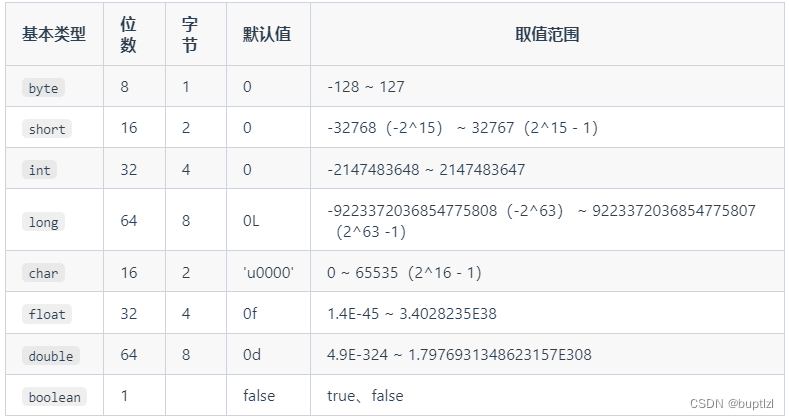
java guide 八股
Java语言特点 简单易学、面向对象(继承、封装、多态)、平台无关性(Java虚拟机jvm)、支持多线程、可靠、安全、高效、支持网络编程、编译与解释共存 JVM:Java虚拟机(跨平台的关键) JREÿ…...

Windows上使用client-go远程访问安装在本地WMware上的Linux虚拟机里的minikube
我在自己的Windows上安装了WMware,并在WMware上安装了CentOS操作系统,然后在CentOS上创建了一个叫minikube的用户,使用minikube用户启动了一个minikube集群,但是我在Windows上使用client-go并无法连通minikube,搜遍全网…...

Linux/Ubuntu/Debian基本命令:命令行历史记录
一组与类 Unix 环境中的命令行(Terminal)历史记录和命令调用相关的键盘快捷键: Ctrl R: 启动对以前使用过的命令的反向搜索。 当你键入时,它将查找并显示与输入的字符匹配的最新命令。Ctrl G: 退出历史搜索模式,不运行命令。 如…...

倒计时32天
L1-032 Left-pad - 2024团体程序设计天梯赛(历年真题)练习集 (pintia.cn) #include<bits/stdc.h> using namespace std; #define int long long const int N2e56; const int inf0x3f3f3f3f; void solve() {int n;char s;cin>>n>>s;ge…...
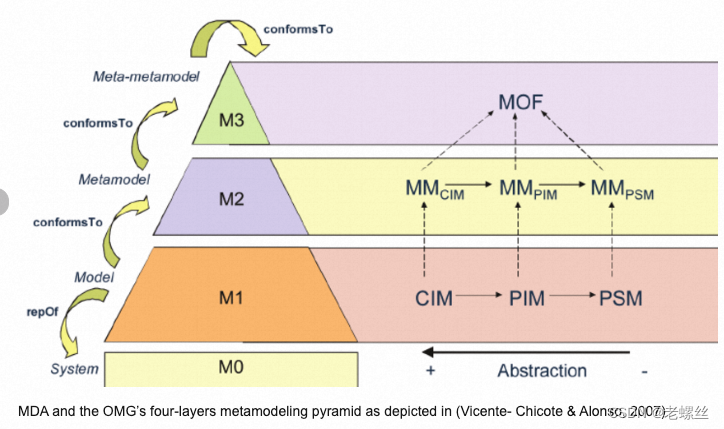
模型驱动架构MDA
MDE 模型驱动工程(MDE, Model-Driven Engineering)是软件工程的一个分支,它将模型与建模拓展到软件开发的所有方面,形成一个多维建模空间,从而将工程活动建立在这些模型的映射和转换之上。[1] MDE的基本原则是将模型视…...

std::error::Error 和 std::io::Error 的区别和用法
std::error::Error 和 std::io::Error 在 Rust 中都是用于错误处理的类型,但它们各自有不同的用途和场景。 std::error::Error: std::error::Error 是一个 trait,它定义了错误处理的基本接口。这个 trait 通常由其他具体的错误类型实现&…...
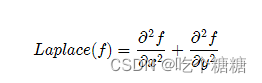
16 OpenCV Laplance算子
文章目录 图像的二阶导数Laplance算子代码示例 图像的二阶导数 在二阶导数的时候,最大变化处的值为零即边缘是零值。通过二阶 导数计算,依据此理论我们可以计算图像二阶导数,提取边缘。 Laplance算子 void Laplacian( InputArray src, Output…...
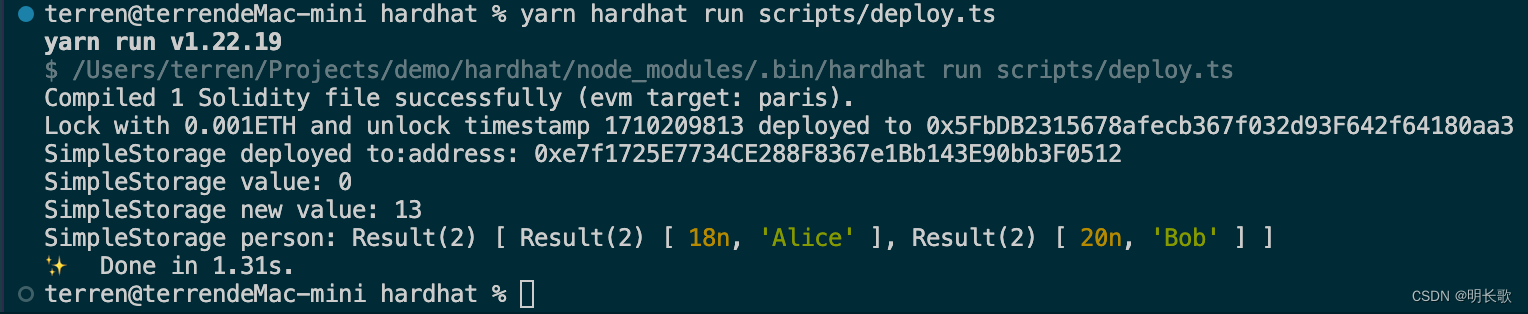
hardhat学习笔记
hardhat学习笔记会不定时填充内容。 初始化项目 yarn init 安装hardhat依赖 yarn add --dev hardhat 初始化 Hardhat yarn hardhat 代码格式化 yarn add --dev prettier prettier-plugin-solidity 项目中增加.prettierrc 与 .prettierignore 配置文件统一格式࿰…...

算法刷题day28
目录 引言一、截断数组二、双端队列三、日期统计 引言 这几道题是周赛里的几道题目,第一道题目我没用这种方法,但还是做出来了,用的一种比较特殊的思考方法,就是把每一个点都判断出来,不满足要求的就舍弃,…...
vivado 使用Design Runs窗口、
使用Design Runs窗口 “设计运行”窗口显示在项目中创建的所有合成和实现运行。它包括用于配置、管理和启动运行的命令。 打开Design Run窗口 选择窗口 → Design Runs打开“Design Runs”窗口。 设计运行窗口功能 •每个实现运行都缩进显示在其子级的合成运行下面。 …...

基于YOLOv8的手机摄像头的自动检测系统
文章大纲 数据集网络爬虫开源数据集标注目标定义标注标准标注工具标签更换脚本自制数据集下载地址自动检测系统设计与搭建模型训练与准确率代码仓库下载地址参考文献与学习路径随着移动通信技术的飞速发展,消费者对移动终端的要求也越来越高,各厂商纷纷提出自己的特色卖点,其…...
)
Ubuntu18.04添加内核模块(字符设备)
Ubuntu18.04添加内核模块(字符设备) 虚拟机Ubuntu18.04(内核版本linux-5.4.0-135-generic) 参考 嵌入式Linux驱动开发(一)——字符设备驱动框架入门 1 编译内核模块 创建字符设备代码文件char_dev.c&a…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
