图论（二）之最短路问题

最短路

Dijkstra求最短路

栗题

https://www.acwing.com/problem/content/851/

https://www.acwing.com/problem/content/852/

思想

迪杰斯特拉算法采用的是一种贪心的策略。

求源点到其余各点的最短距离步骤如下：

1. 用一个 dist 数组保存源点到其余各个节点的距离，dist[i] 表示源点到节点 i 的距离。初始时，dist 数组的各个元素为无穷大。
   用一个状态数组 state 记录是否找到了源点到该节点的最短距离，state[i] 如果为真，则表示找到了源点到节点 i 的最短距离，state[i] 如果为假，则表示源点到节点 i 的最短距离还没有找到。初始时，state 各个元素为假。

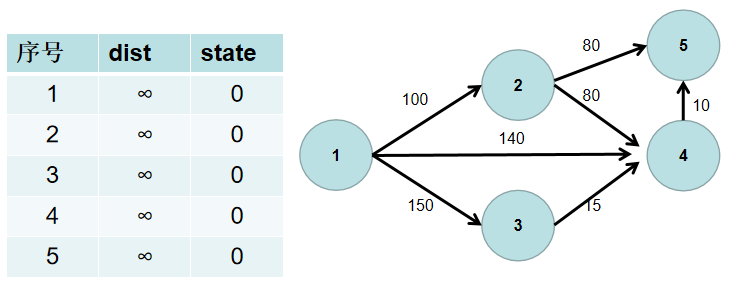
2. 源点到源点的距离为 0。即dist[1] = 0。

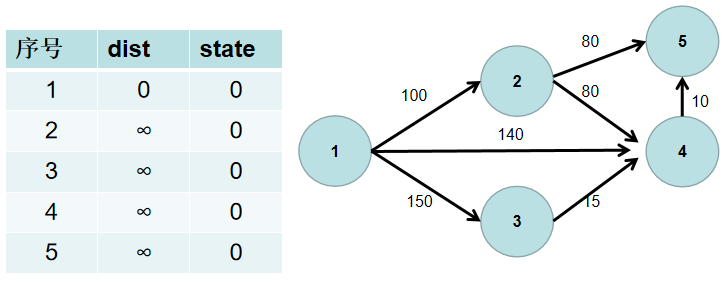
3. 遍历 dist 数组，找到一个节点，这个节点是：没有确定最短路径的节点中距离源点最近的点。假设该节点编号为 i。此时就找到了源点到该节点的最短距离，state[i] 置为 1。

   

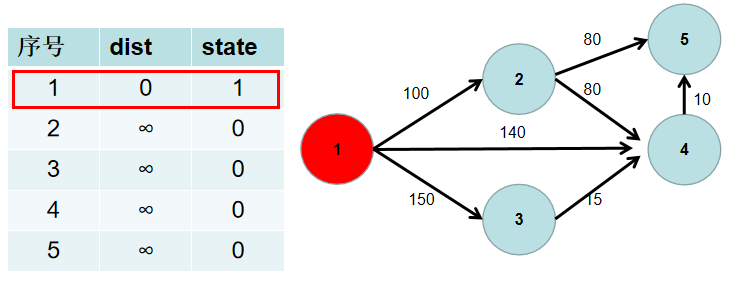
4. 遍历 i 所有可以到达的节点 j，如果 dist[j] 大于 dist[i] 加上 i -> j 的距离，即 dist[j] > dist[i] + w[i][j]（w[i][j] 为 i -> j 的距离） ，则更新 dist[j] = dist[i] + w[i][j]。

   

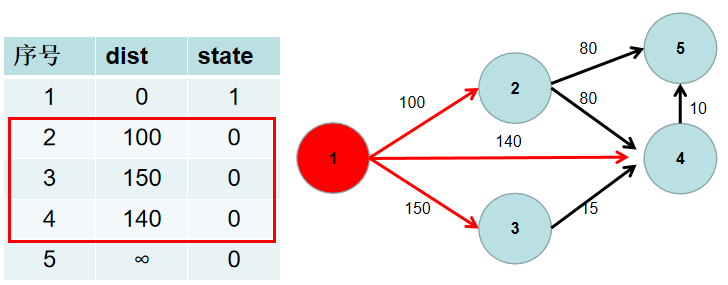
5. 重复 3 4 步骤，直到所有节点的状态都被置为 1。

   

6. 此时 dist 数组中，就保存了源点到其余各个节点的最短距离。

   

题目

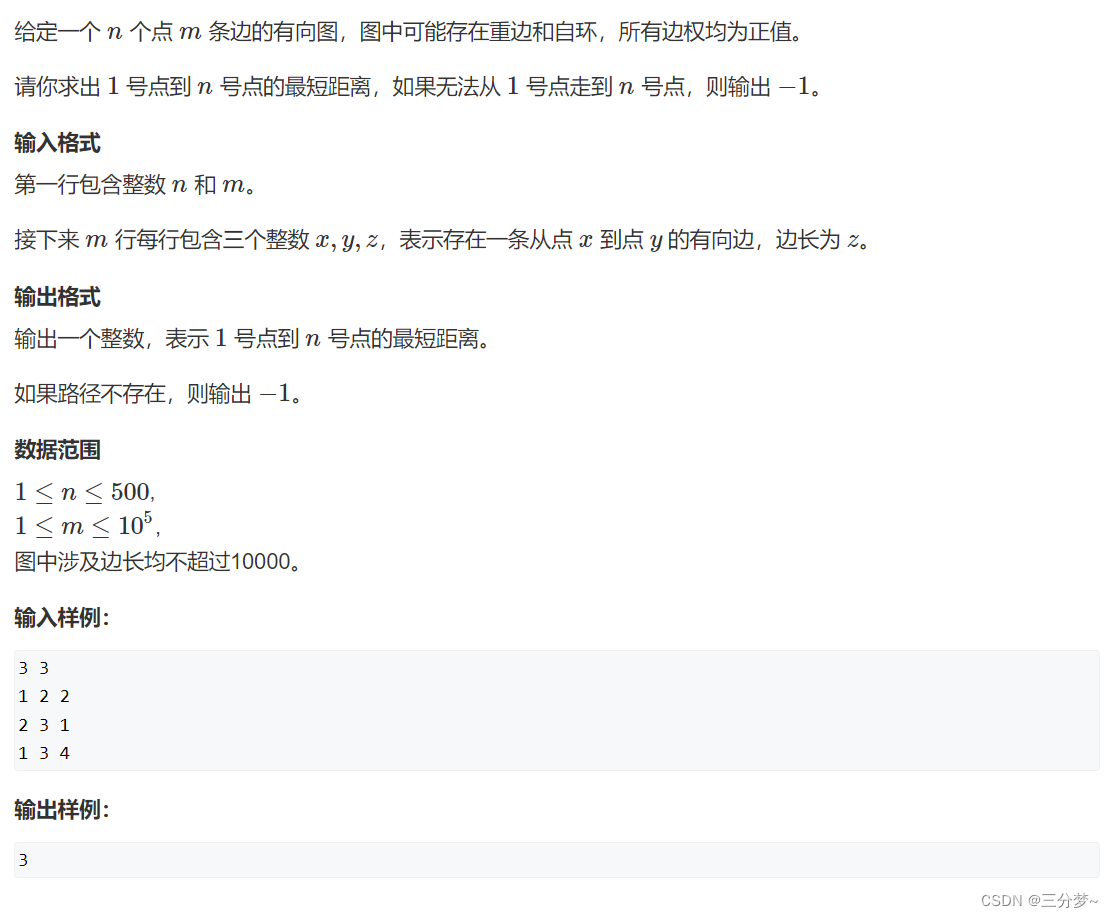
代码

#include<iostream>
#include <cstring>
#include <algorithm>
using namespace std;const int N = 510, M = 100010;int h[N], e[M], ne[M], w[M], idx;//邻接表存储图
int state[N];//state 记录是否找到了源点到该节点的最短距离
int dist[N];//dist 数组保存源点到其余各个节点的距离
int n, m;//图的节点个数和边数void add(int a, int b, int c)//插入边
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}void Dijkstra()
{memset(dist, 0x3f, sizeof(dist));//dist 数组的各个元素为无穷大dist[1] = 0;//源点到源点的距离为置为 0for (int i = 0; i < n; i++){int t = -1;for (int j = 1; j <= n; j++)//遍历 dist 数组，找到没有确定最短路径的节点中距离源点最近的点t{if (!state[j] && (t == -1 || dist[j] < dist[t]))t = j;}state[t] = 1;//state[i] 置为 1。for (int j = h[t]; j != -1; j = ne[j])//遍历 t 所有可以到达的节点 i{int i = e[j];dist[i] = min(dist[i], dist[t] + w[j]);//更新 dist[j]}}
}int main()
{memset(h, -1, sizeof(h));//邻接表初始化cin >> n >> m;while (m--)//读入 m 条边{int a, b, w;cin >> a >> b >> w;add(a, b, w);}Dijkstra();if (dist[n] != 0x3f3f3f3f)//如果dist[n]被更新了，则存在路径cout << dist[n];elsecout << "-1";
}

---

优化

下面进行优化，可以看出上方时间复杂度为$O(n^2)$， 查找距离源点最近的点没有被确定的点t需要$O(n)$，遍历t所有可以到达的节点 i需要$O(n)$， 而这可以进行优化

• 若是用小根堆（优先队列）进行存储， 那么每次找距离最近的那个点t只需要$O(1)$，而遍历t所有可以到达的需要$O(mlo{g}_n)$因为堆的修改需要$O(lo{g}_n)$

代码如下

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 150010;
//用邻接表的话重边可以不用考虑
typedef pair<int, int> PII;
int h[N], w[N], ne[N], idx, e[N];
int n, m;
bool st[N];
int dist[N];
void add(int a, int b, int c) {e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}int dijkstra() {memset(dist, 0x3f3f3f3f, sizeof dist);dist[1] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap;heap.push({0, 1});  //{距离，编号}while(heap.size()) {auto t = heap.top();heap.pop();int no = t.second, distance = t.first;if(st[no])  continue;   //若此编号已经找到距离，那么跳过st[no] = true;for(int i = h[no]; i != -1; i = ne[i]) {int j = e[i];if(dist[j] > dist[no] + w[i]) {dist[j] = dist[no] + w[i];heap.push({dist[j], j});}}}if(dist[n] == 0x3f3f3f3f)   return -1;return dist[n];
}int main() {scanf("%d%d", &n, &m);//邻接表第一步的必备memset(h, -1, sizeof h);while(m --) {int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}int t = dijkstra();cout << t;return 0;
}

---

bellman-ford

算法分析

1、问题：为什么Dijkstra不能使用在含负权的图中？
（这是以前错误的分析，若看完这个例子分析觉得正确的说明对最短路理解得还不够透彻，这里不做删除）
分析：如图所示：
若通过Dijkstra算法可以求出从1号点到达4号点所需的步数为3 (每次选择离源点最短距离的点更新其他点)
但实际上从 1 号点到达 4 号点所需步数为 1 (1 –> 2 –> 3),因此不能使用 Dijkstra 解决含负权图的问题

正确的分析
Dijkstra算法的3个步骤

1、找到当前未标识的且离源点最近的点t
2、对t号点点进行标识
3、用t号点更新其他点的距离
反例

结果：

dijkstra算法在图中走出来的最短路径是1 -> 2 -> 4 -> 5，算出 1 号点到 5 号点的最短距离是2 + 2 + 1 = 5，然而还存在一条路径是1 -> 3 -> 4 -> 5，该路径的长度是5 + (-2) + 1 = 4，因此 dijkstra 算法失效

dijkstra详细步骤

• 初始dist[1] = 0`

• 找到了未标识且离源点1最近的结点1，标记1号点，用1号点更新其他所有点的距离，2号点被更新成dist[2] = 2，3号点被更新成

  dist[3] = 5

• 找到了未标识且离源点1最近的结点2，标识2号点，用2号点更新其他所有点的距离，4号点被更新成dist[4] = 4

• 找到了未标识且离源点1最近的结点4，标识4号点，用4号点更新其他所有点的距离，5号点被更新成dist[5] = 5

• 找到了未标识且离源点1最近的结点3，标识3号点，用3号点更新其他所有点的距离，4号点被更新成dist[4] = 3
  结束

• 得到1号点到5号点的最短距离是5，对应的路径是1 -> 2 -> 4 -> 5，并不是真正的最短距离

2、什么是bellman - ford算法？
Bellman - ford 算法是求含负权图的单源最短路径的一种算法，效率较低，代码难度较小。其原理为连续进行松弛，在每次松弛时把每条边都更新一下，若在 n-1 次松弛后还能更新，则说明图中有负环，因此无法得出结果，否则就完成。
(通俗的来讲就是：假设 1 号点到 n 号点是可达的，每一个点同时向指向的方向出发，更新相邻的点的最短距离，通过循环 n-1 次操作，若图中不存在负环，则 1 号点一定会到达 n 号点，若图中存在负环，则在 n-1 次松弛后一定还会更新)

3、bellman - ford算法的具体步骤

for n次for 所有边 a,b,w (松弛操作)dist[b] = min(dist[b],back[a] + w)

注意：back[] 数组是上一次迭代后 dist[] 数组的备份，由于是每个点同时向外出发，因此需要对 dist[] 数组进行备份，若不进行备份会因此发生串联效应，影响到下一个点

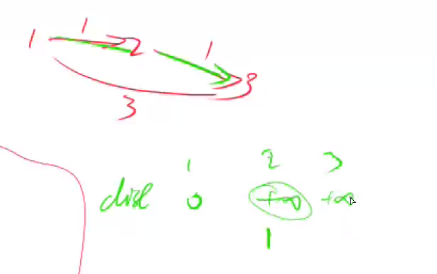
为什么需要back[a]数组
为了避免如下的串联情况， 在边数限制为一条的情况下，节点3的距离应该是3，但是由于串联情况，利用本轮更新的节点2更新了节点3的距离，所以现在节点3的距离是2。

正确做法是用上轮节点2更新的距离–无穷大，来更新节点3， 再取最小值，所以节点3离起点的距离是3。

for (int i = 0; i < k; i ++ )
{memcpy(backup, dist, sizeof dist);for (int j = 0; j < m ; j ++ ){int a = edges[j].a, b = edges[j].b, w = edges[j].w;dist[b] = min(dist[b], backup[a] + w);}
}

4、在下面代码中，是否能到达n号点的判断中需要进行if(dist[n] > INF/2)判断，而并非是if(dist[n] == INF)判断，原因是INF是一个确定的值，并非真正的无穷大，会随着其他数值而受到影响，dist[n]大于某个与INF相同数量级的数即可

5、bellman - ford算法擅长解决有边数限制的最短路问题
时间复杂度 O(nm)

其中n为点数，m为边数

作者：小呆呆
链接：https://www.acwing.com/solution/content/6320/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

只能用bellman-ford来解决的题型

有边数限制的最短路

这里题目说了可能为负权边或者负权回路，那么就不能用dijkstra和spfa算法

dijkstra不能解决负权边是因为 dijkstra要求每个点被确定后st[j] = true，dist[j]就是最短距离了，之后就不能再被更新了（一锤子买卖），而如果有负权边的话，那已经确定的点的dist[j]不一定是最短了

题目

完整代码

```cpp
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 510, M = 10010;struct Edge
{int a, b, c;
}edges[M];int n, m, k;
int dist[N];
int last[N];void bellman_ford()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < k; i ++ ){memcpy(last, dist, sizeof dist);for (int j = 0; j < m; j ++ ){auto e = edges[j];dist[e.b] = min(dist[e.b], last[e.a] + e.c);}}
}int main()
{scanf("%d%d%d", &n, &m, &k);for (int i = 0; i < m; i ++ ){int a, b, c;scanf("%d%d%d", &a, &b, &c);edges[i] = {a, b, c};}bellman_ford();if (dist[n] > 0x3f3f3f3f / 2) puts("impossible");else printf("%d\n", dist[n]);return 0;
}```

---

spfa求最短路

spfa 算法思路

明确一下松弛的概念。

• 考虑节点u以及它的邻居v，从起点跑到v有好多跑法，有的跑法经过u，有的不经过。

• 经过u的跑法的距离就是dist[u]+u到v的距离。

• 所谓松弛操作，就是看一看dist[v]和dist[u]+u到v的距离哪个大一点。

• 如果前者大一点，就说明当前的不是最短路，就要赋值为后者，这就叫做松弛。

spfa算法文字说明：

• 一个队列，初始时队列里只有起始点。

• 再建立一个数组记录起始点到所有点的最短路径（该表格的初始值要赋为极大值，该点到他本身的路径赋为0）。

• 再建立一个数组，标记点是否在队列中。

• 队头不断出队，计算始点起点经过队头到其他点的距离是否变短，如果变短且被点不在队列中，则把该点加入到队尾。

• 重复执行直到队列为空。

• 在保存最短路径的数组中，就得到了最短路径。

spfa 图解：

• 给定一个有向图，如下，求A~E的最短路。

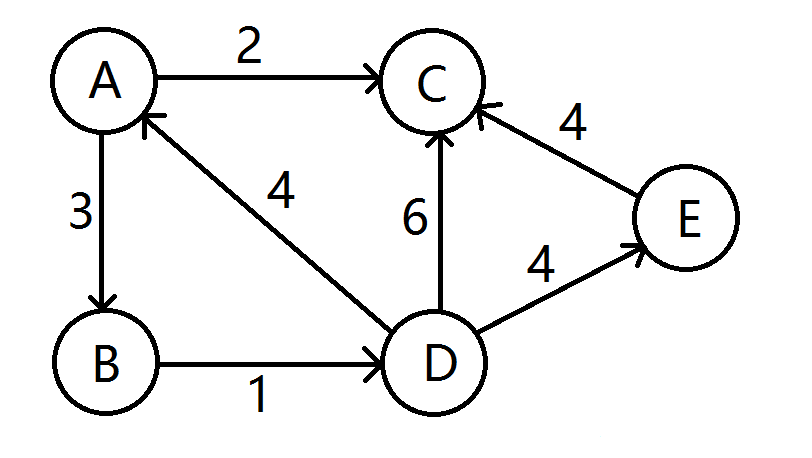
• 源点A首先入队，然后A出队，计算出到BC的距离会变短，更新距离数组，BC没在队列中，BC入队

• B出队，计算出到D的距离变短，更新距离数组，D没在队列中，D入队。然后C出队，无点可更新。

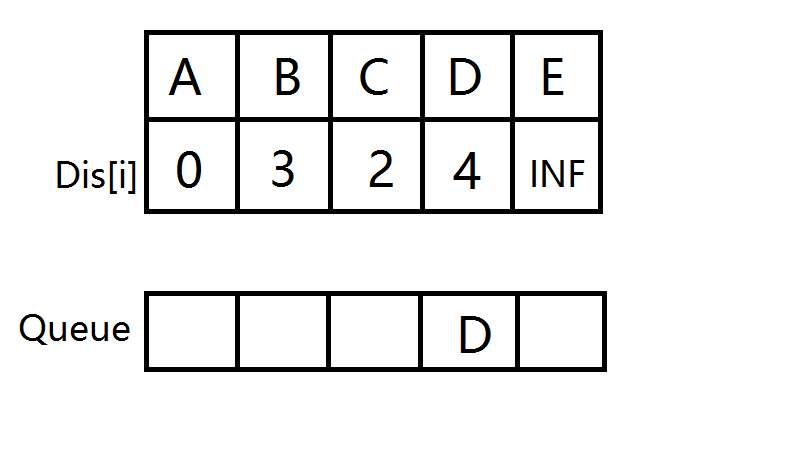
• D出队，计算出到E的距离变短，更新距离数组，E没在队列中，E入队。

• 

• E出队，此时队列为空，源点到所有点的最短路已被找到，A->E的最短路即为8

  

题目

https://www.acwing.com/problem/content/853/

完整代码

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 100010;
int w[N], h[N], idx, ne[N], e[N];
int n, m;
int dist[N];    //各点到源点的距离
bool st[N];
void add(int a, int b, int c) {e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}int spfa() {memset(dist, 0x3f3f3f3f, sizeof dist);dist[1] = 0;queue<int> q;    q.push(1);st[1] = true;   //代表在队列中了while(q.size()) {auto t = q.front();q.pop();st[t] = false;for(int i = h[t]; i != -1; i = ne[i]) {int j = e[i];if(dist[j] > dist[t] + w[i]) {dist[j] = dist[t] + w[i];if(!st[j]) {q.push(j);st[j] = true;   //在队列中了}}}}return dist[n];
}int main() {memset(h, -1, sizeof h);cin >> n >> m;while(m --) {int a, b, w;scanf("%d%d%d", &a, &b, &w);add(a, b, w);}int res = spfa();if(res == 0x3f3f3f3f)   cout << "impossible";else cout << res;return 0;
}

总结tips

---

spfa判断负环

https://www.acwing.com/problem/content/854/

算法分析

使用spfa算法解决是否存在负环问题

求负环的常用方法，基于SPFA，一般都用方法 2（该题也是用方法 2）：

• 方法 1：统计每个点入队的次数，如果某个点入队n次，则说明存在负环-
• 方法 2：统计当前每个点的最短路中所包含的边数，如果某点的最短路所包含的边数大于等于n，则也说明存在环

1. dist[x] 记录虚拟源点到x的最短距离

2. cnt[x] 记录当前x点到虚拟源点最短路的边数，初始每个点到虚拟源点的距离为0，只要他能再走n步，即cnt[x] >= n，则表示该图中一定存在负环，由于从虚拟源点到x至少经过n条边时，则说明图中至少有n + 1个点，表示一定有点是重复使用

3. 若dist[j] > dist[t] + w[i],则表示从t点走到j点能够让权值变少，因此进行对该点j进行更新，并且对应cnt[j] = cnt[t] + 1,往前走一步

注意：该题是判断是否存在负环，并非判断是否存在从1开始的负环，因此需要将所有的点都加入队列中，更新周围的点

故只需要对上方代码稍做改动即可：

代码如下

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 100010;
int w[N], h[N], idx, ne[N], e[N];
int n, m;
int dist[N];    //各点到源点的距离
int cnt[N]; //存储边的个数
bool st[N];
void add(int a, int b, int c) {e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}int spfa() {memset(dist, 0x3f3f3f3f, sizeof dist);	dist[1] = 0;			queue<int> q;    for(int i = 1; i <= n; i++) {st[i] = true;q.push(i);}while(q.size()) {auto t = q.front();q.pop();st[t] = false;for(int i = h[t]; i != -1; i = ne[i]) {int j = e[i];if(dist[j] > dist[t] + w[i]) {dist[j] = dist[t] + w[i];cnt[j] = cnt[t] + 1;if(cnt[j] > n)  return true;if(!st[j]) {q.push(j);st[j] = true;   //在队列中了}}}}return false;
}int main() {memset(h, -1, sizeof h);cin >> n >> m;while(m --) {int a, b, w;scanf("%d%d%d", &a, &b, &w);add(a, b, w);}bool res = spfa();if(res) cout << "Yes";else cout << "No";return 0;
}

---

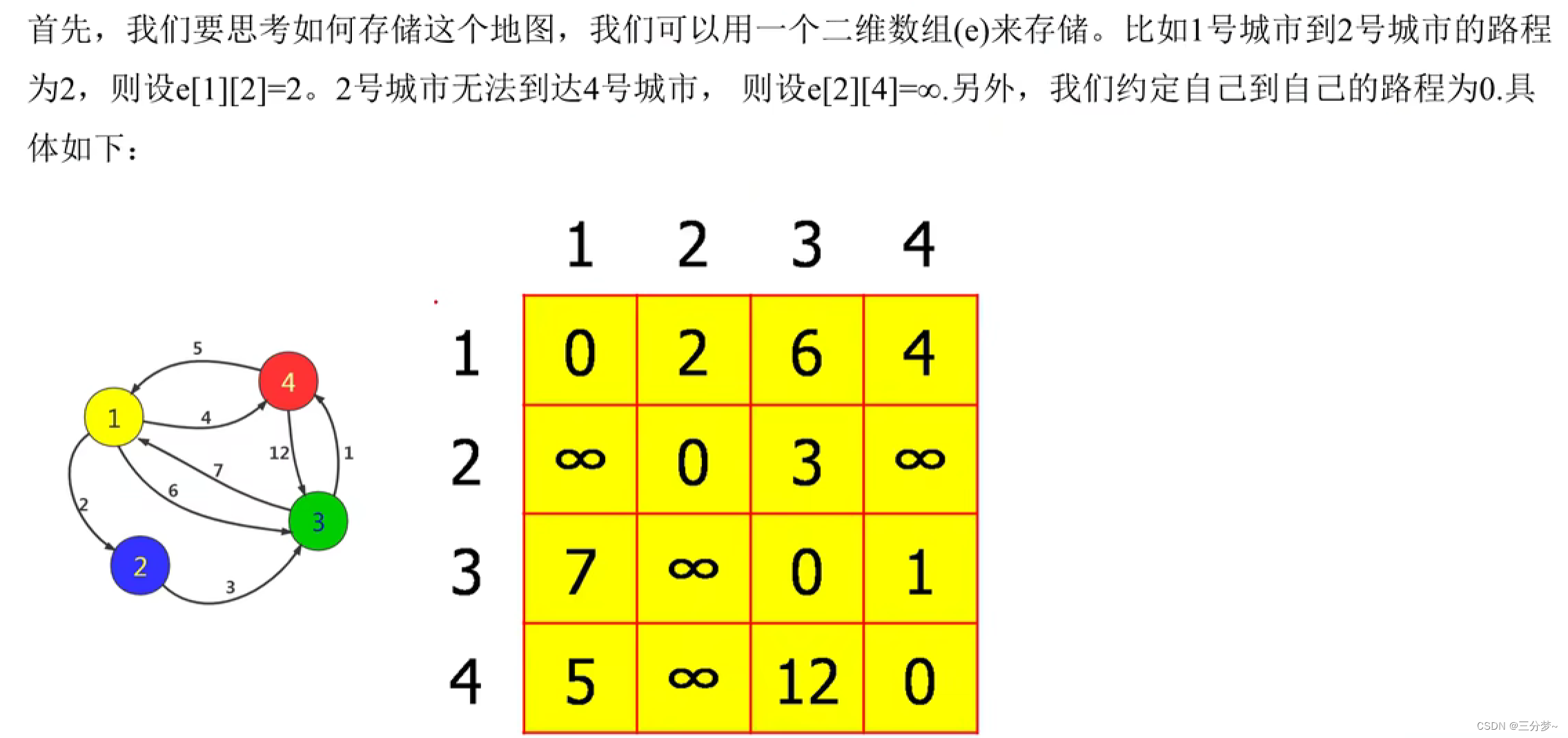
Floyd求最短路

求多源最短路

通过中转和动态规划来递推出最短路径距离

从i到j经过k，通过三重循环来实现

初始化自环为0，其他为INF

对于重边的情况下，我们初始化取最小距离

模拟过程

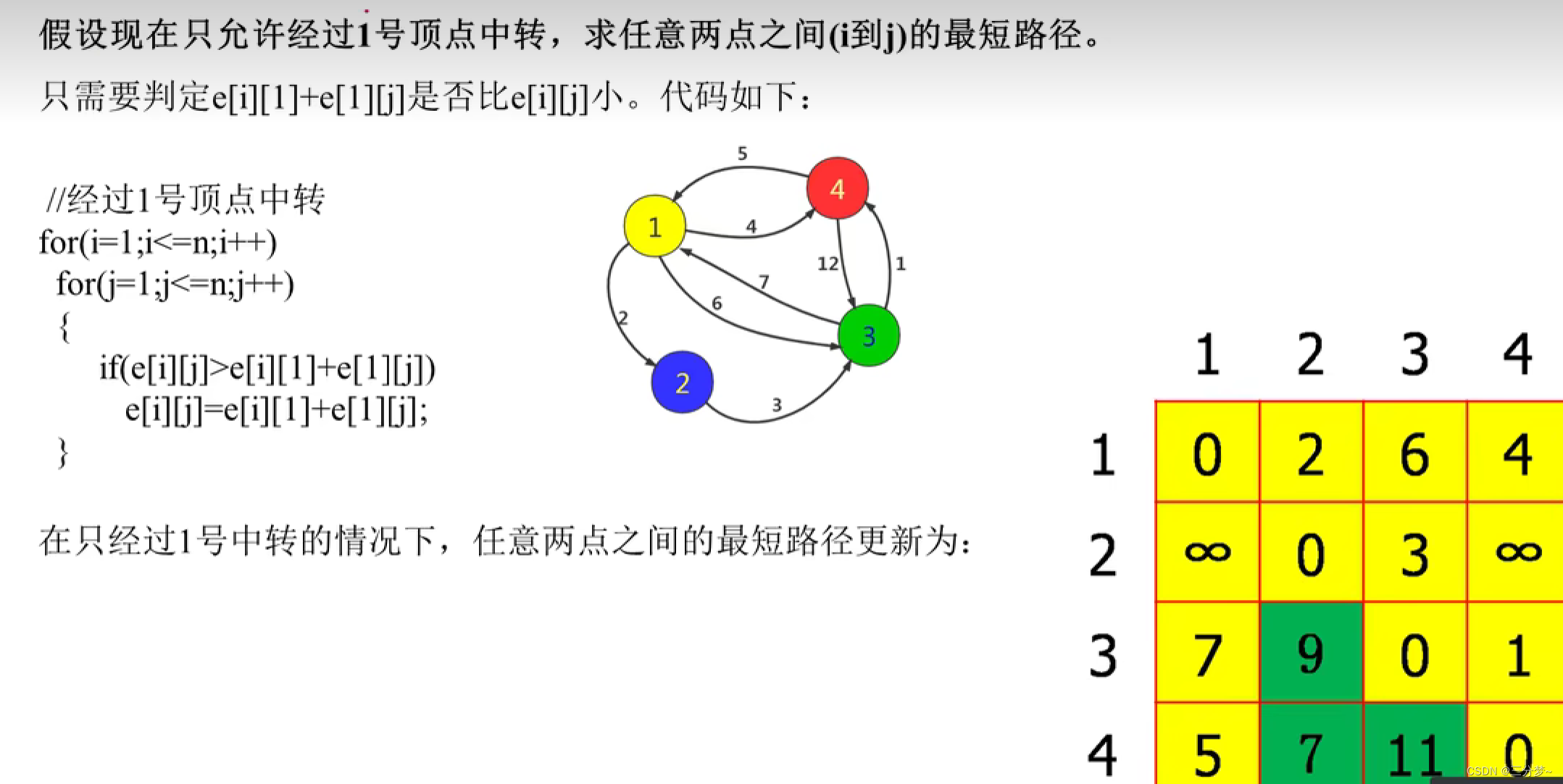
链接：https://www.acwing.com/problem/content/856/

题目

代码如下

using namespace std;
const int N = 210, INF = 1e9;
int n, m, Q;
int d[N][N];
void floyd() {for(int k = 1; k <= n; k++)		//依次经过1~n中的n各点进行中转for(int i = 1; i <= n; i++)for(int j = 1; j <= n; j++)d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
int main() {cin >> n >> m >> Q;//初始化处理重边和自环for(int i = 1; i <= n; i++)for(int j = 1; j <= n; j++)if(i == j)  d[i][j] = 0;else d[i][j] = INF;while(m --) {int x, y, z;scanf("%d%d%d", &x, &y, &z);d[x][y] = min(d[x][y], z);}floyd();while(Q --) {int a, b;scanf("%d%d", &a, &b);int res = d[a][b];if(res > INF / 2) printf("impossible\n");else cout << res << '\n';}return 0;
}