神经网络线性量化方法简介
可点此跳转看全篇
目录
- 神经网络量化
- 量化的必要性
- 量化方法简介
- 线性对称量化
- 线性非对称量化方法

神经网络量化
量化的必要性
| Network | Model size (MB) | GFLOPS |
|---|---|---|
| AlexNet | 233 | 0.7 |
| VGG-16 | 528 | 15.5 |
| VGG-19 | 548 | 19.6 |
| ResNet-50 | 98 | 3.9 |
| ResNet-101 | 170 | 7.6 |
| ResNet-152 | 230 | 11.3 |
| GoogleNet | 27 | 1.6 |
| InceptionV3 | 89 | 6 |
| MobileNet | 38 | 0.58 |
| SequeezeNet | 30 | 0.84 |
随着网络的深度变大,参数变多,神经网络消耗越来越多的算力,占用原来越大的存储资源。
若想在移动设备和嵌入式设备上运行深度学习神经网络,如此庞大的网络参数将对移动设备的运行内存和总线带宽资源造成巨大消耗。目前三个方向:
1)研究新型的轻量网络或者微型网络:设计更高效的新型网络架构,用相对较小的网络模型达到可接受的预测准确度(如MobileNet和SequeezeNet等)。
2)研究现有网络的参数缩减:如网络剪枝,参数量化等;
3)研究新型计算模型、体系结构和计算部件:如内存中计算、忆阻器等
量化方法简介
大多数网络模型都采用32位浮点数(FP32)来存储网络参数。如果改用较低精度的16位浮点数(FP16)来存储网络参数,那么网络模型就可以减小一半。
常用的低精度表示方法有16位定点数(INT16)、8位定点数(INT8)、4位定点数(INT4)、二进制(INT1)等。其中,使用INT1量化的网络称为二元神经网络(Binary Neural Network, BNN)。
根据网络参数到特定位宽定点数的映射类型,可将量化策略可分为线性量化和非线性量化两种。线性量化策略将所有的网络参数线性映射到特定量化精度的数据范围中。例如,如果某神经网络的参数值在[0.05, 12]范围内,假设采用INT8的线性量化策略,那么区间[0.05, 12]将被线性映射到[0, 255]。非线性策略则根据神经网络的参数密度,在线性量化策略的基础上进行调整。与线性量化策略相比,非线性量化策略能够将网络参数更均匀地映射到定点数区间,因此其量化效果较好,对预测精度的影响较小。
此外,根据量化后的网络参数是否关于坐标轴原点对称,可将量化策略分为对称量化和非对称量化两种。对称量化策略将网络参数映射到关于坐标原点对称的区间。例如,假设网络参数的取值范围是[-3, 6],若采用INT8的对称量化策略,则[-3, 6]将被映射到[-127, 127]。非对称量化允许将网络参数映射到不对称的区间。与对称量化策略相比,非对称量化策略能够将网络参数更均匀地映射到定点数区间,因此其量化效果较好,对预测精度的影响较小。
从经验上讲,当量化精度低于INT8时,量化后网络的精度急速下降。因此工业界目前普遍采用INT8的量化精度。
线性对称量化
首先找出每个网络层中参数取值区间端点绝对值的最大值MAX,然后将网络参数所在的[-MAX, MAX]的区间线性映射到[-127, 127]。
[!Note] 举例
假设某个网络层的参数在[-3,6]之间,最大值MAX为6。需要将[-6,6]线性映射到[-127,127],那么6可以用127表示,-3用-63表示。因为原本参数为FP32,而现在是INT8,所以能够将网络参数的大小缩小75%。
INT8线性对称量化步骤如下:
- 计算参数所在区间的端点 [ a , b ] [a,b] [a,b]绝对值的最大值 M A X = m a x { ∣ a ∣ , ∣ b ∣ } MAX=max\{|a|,|b|\} MAX=max{∣
相关文章:

神经网络线性量化方法简介
可点此跳转看全篇 目录 神经网络量化量化的必要性量化方法简介线性对称量化线性非对称量化方法神经网络量化 量化的必要性 NetworkModel size (MB)GFLOPSAlexNet2330.7VGG-1652815.5VGG-1954819.6ResNet-50983.9ResNet-1011707.6ResNet-15223011.3GoogleNet271.6InceptionV38…...

阿里云k8s内OSS报错UnKnownHost。
这个问题就是链接不上oss属于网络问题: 1.排查服务器 在服务器(ecs)上直接ping oss地址看是否能够通。 不通就要修改dns和hosts(这个不说,自己网上查) 2.排查容器 进去ping一下你的容器是否能访问到oss…...
nginx的使用,homebrew安装及使用nginx。
Nginx 是一个高性能的 HTTP 和反向代理服务器,它提供了诸如 IMAP、POP3 和 SMTP 等邮件代理服务。以下是 Nginx 的主要作用:12345 作为 Web 服务器。Nginx 能够以较少的系统资源提供高效率的服务,尤其在高并发连接下表现出色。1…...

计算机等级考试:信息安全技术 知识点六
1、P2DR模型是美国ISS公司提出的动态网络安全体系的代表模型,可用数学公式表达为Pt>DtRt,其中Pt表示:系统防护时间。 2、美国联邦政府颁布数字签名标准(Digital Signature Standard,DSS)的年份是1994 3、密码分析者(攻击者)已…...

vue provide 与 inject使用
在vue项目中,如果遇到跨组件多层次传值的话,一般会用到vuex,或者其他第三方共享状态管理模式,如pinia等,但是对于父组件与多层次孙子组件时,建议使用provide 与 inject,与之其他方式相比&#x…...

Vue3.0 所采用的 Composition Api 与 Vue2.x 使用的 Options Api 有什么不同?
开始之前 Composition API 可以说是Vue3的最大特点,那么为什么要推出Composition Api,解决了什么问题? 通常使用Vue2开发的项目,普遍会存在以下问题: 代码的可读性随着组件变大而变差每一种代码复用的方式ÿ…...
php集成修改数据库的字段
1.界面效果 2.代码 <?phpecho <form action"" method"post"><label for"table">表名:</label><input type"text" id"table" name"table"><br><div id"fieldsContaine…...
爬虫技术之正则提取静态页面数据
第一天 简单示例 在爬虫过程中,我们获取到了页面之后,通常需要做的就是解析数据,将数据持久化到数据库为我所用。如何又快又准确得提取有效数据?这是一门技术,看了我的博客之前可能略有难度,但各位大师看…...

字符串匹配算法:暴力匹配、KMP 算法、Boyer-Moore 算法、Rabin-Karp 算法
字符串匹配算法 字符串匹配算法是在一个字符串(称为文本)中查找另一个字符串(称为模式)出现的位置或者是否存在的算法。常见的字符串匹配算法包括暴力匹配、KMP算法、Boyer-Moore算法和Rabin-Karp算法。下面是对这些算法的简要介…...
微信小程序接入百度地图(微信小程序插件)使用文档
第一步配置域名 :在微信公众平台登录后配置服务域名称:https://apis.map.qq.com 第二步申请密钥 申请开发者密钥申请地址 第三步使用插件 选择添加插件 搜索腾讯位置服务地图选点 选择要授权的小程序 授权完毕会在这里显示插件信息 第四步查看使用文档 跳转至文…...

如果需要在Log4j中记录特定的异常信息,应该如何实现?如何动态地更改Log4j的日志级别?
如果需要在Log4j中记录特定的异常信息,应该如何实现? 在Log4j中记录特定的异常信息,你可以使用Logger类的error、warn、info等方法,这些方法通常接受一个字符串消息和一个Throwable对象(如异常)作为参数。下…...
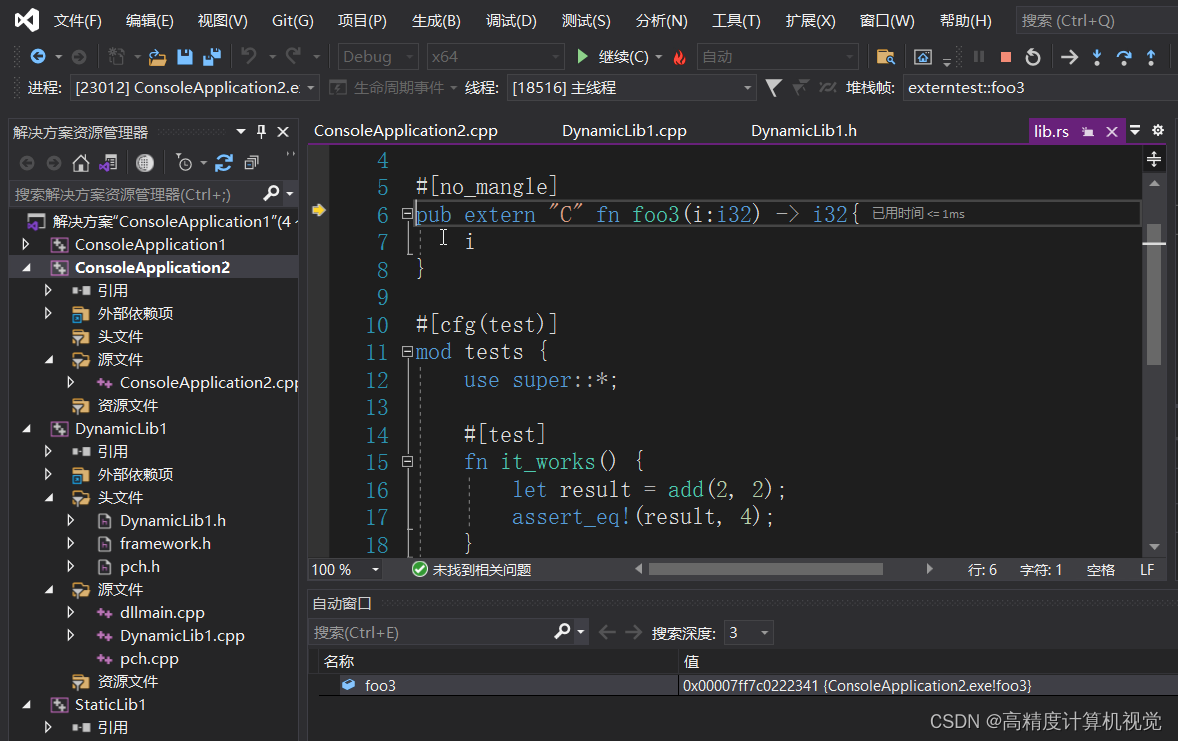
Rust入门:C++和Rust动态库(dll)的相互调用
无论是C调用Rust动态库还是Rust调用C动态库,其操作基本都是一样地简单,基本和C调用C的动态库没什么区别,只需要列出所需要导入的函数,并链接到相应的lib文件即可。 这里,在windows中,我们以dll动态库为例说…...

第三篇【传奇开心果系列】Python的自动化办公库技术点案例示例:深度解读Pandas股票市场数据分析
传奇开心果博文系列 系列博文目录Python的自动化办公库技术点案例示例系列 博文目录前言一、Pandas进行股票市场数据分析常见步骤和示例代码1. 加载数据2. 数据清洗和准备3. 分析股票价格和交易量4. 财务数据分析 二、扩展思路介绍1. 技术指标分析2. 波动性分析3. 相关性分析4.…...

3.11笔记2
目前使用的格里高利历闰年的规则如下: 公元年分非4的倍数,为平年。公元年分为4的倍数但非100的倍数,为闰年。公元年分为100的倍数但非400的倍数,为平年。公元年分为400的倍数为闰年。 请用一个表达式 (不能添加括号) 判断某一年…...
web服务器基础
目录 web服务器简介 (1)什么是www (2)网址及HTTP简介 (3)http协议请求的工作流程 主配置文件内的参数 目录标签 缺点 虚拟主机vhosts 示例的格式如下 实例 多IP实现多网页 修改监听端口号 hosts文件及域名解析 修改hosts文件内缓存格式 实现效果 实现多域名解析IP地址 在linux…...
矢量图片转换软件Vector Magic mac中文版功能特色
Vector Magic mac中文版是一款非常流行的矢量图片转换软件,它的功能特色主要体现在以下几个方面: 首先,Vector Magic mac中文版拥有出色的矢量转换能力。它采用世界上最好的全彩色自动描摹器,能够将JPG、PNG、BMP和GIF等位图图像…...
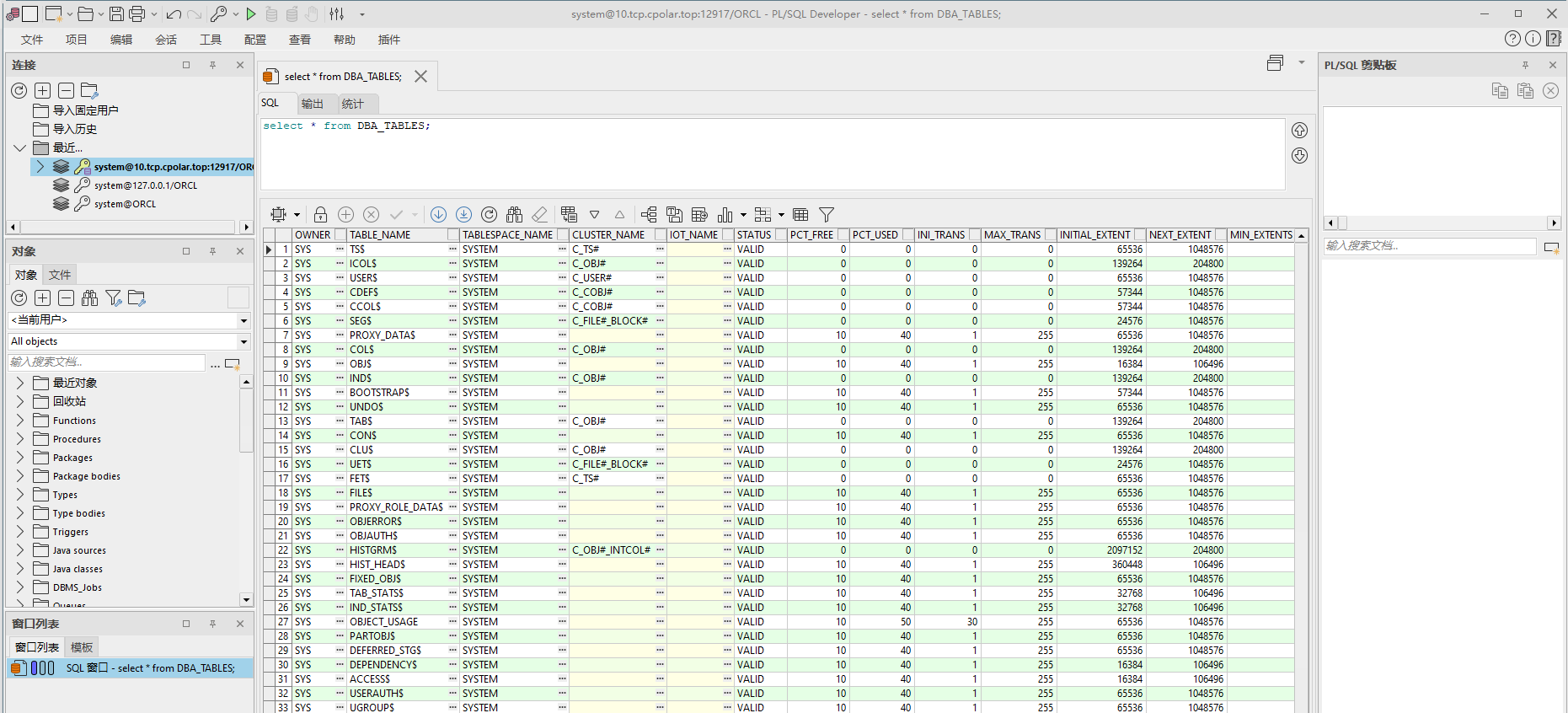
Window部署Oracle并实现公网环境远程访问本地数据库
文章目录 前言1. 数据库搭建2. 内网穿透2.1 安装cpolar内网穿透2.2 创建隧道映射 3. 公网远程访问4. 配置固定TCP端口地址4.1 保留一个固定的公网TCP端口地址4.2 配置固定公网TCP端口地址4.3 测试使用固定TCP端口地址远程Oracle 前言 Oracle,是甲骨文公司的一款关系…...
灵魂指针,教给(三)
欢迎来到白刘的领域 Miracle_86.-CSDN博客 系列专栏 C语言知识 先赞后看,已成习惯 创作不易,多多支持! 目录 一、 字符指针变量 二、数组指针变量 2.1 数组指针变量是什么 2.2 数组指针变量如何初始化 三、二维数组传参本质 四、函数…...
纯手工搭建一个springboot maven项目
前言:idea社区版无法自动搭建项目,手动搭建的经验分享如下: 1 包结构 参考下图: 2 项目结构 3 maven依赖 具体的项目包结构如下图: 依据这个项目包结构配置一个springboot 的 pom依赖: <?xml ve…...

【Java】使用`LinkedList`类来实现一个队列,并通过继承`AbstractQueue`或者实现`Queue`接口来实现自定义队列
使用LinkedList类来实现一个队列,并通过继承AbstractQueue或者实现Queue接口来实现自定义队列。 以下是一个简单的示例,其中队列的大小与另一个List的容量保持一致: import java.util.LinkedList; import java.util.List; import java.util…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
