LeetCode 1315.祖父节点值为偶数的节点和
给你一棵二叉树,请你返回满足以下条件的所有节点的值之和:
该节点的祖父节点的值为偶数。(一个节点的祖父节点是指该节点的父节点的父节点。)
如果不存在祖父节点值为偶数的节点,那么返回 0 。
示例:
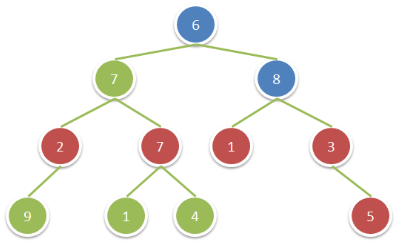
输入:root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]
输出:18
解释:图中红色节点的祖父节点的值为偶数,蓝色节点为这些红色节点的祖父节点。
提示:
树中节点的数目在 1 到 10^4 之间。
每个节点的值在 1 到 100 之间。
法一:直接递归模拟即可:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int sumEvenGrandparent(TreeNode* root) {int ans = 0;findAns(root, false, false, ans);return ans;}private:void findAns(TreeNode *node, bool isEvenFather, bool isEvenGrandFather, int &ans){if (node == nullptr){return;}if (isEvenGrandFather){ans += node->val;}findAns(node->left, !(node->val & 1), isEvenFather, ans);findAns(node->right, !(node->val & 1), isEvenFather, ans);}
};
如果树中有n个节点,此算法时间复杂度为O(n),空间复杂度为O(logn)。
法二:广度优先搜索,每遍历到一个偶数节点,将其孙子节点的值加上:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int sumEvenGrandparent(TreeNode* root) {queue<TreeNode *> q;q.push(root);int ans = 0;while (!q.empty()){TreeNode *node = q.front();q.pop();if (!(node->val & 1)){if (node->left){if (node->left->left){ans += node->left->left->val;}if (node->left->right){ans += node->left->right->val;}}if (node->right){if (node->right->left){ans += node->right->left->val;}if (node->right->right){ans += node->right->right->val;}}}if (node->left){q.push(node->left);}if (node->right){q.push(node->right);}}return ans;}
};
如果树中有n个节点,此算法时间复杂度为O(n),空间复杂度为O(logn)。
相关文章:

LeetCode 1315.祖父节点值为偶数的节点和
给你一棵二叉树,请你返回满足以下条件的所有节点的值之和: 该节点的祖父节点的值为偶数。(一个节点的祖父节点是指该节点的父节点的父节点。) 如果不存在祖父节点值为偶数的节点,那么返回 0 。 示例: 输入…...

C语言分支和循环总结
文章目录 概要结构介绍不同结构的语句简单运用小结 概要 C语言中分为三种结构:顺序结构,选择结构,循环结构 结构介绍 顺序结构就是从上到下,从左到右等等;选择结构可以想象是Y字路口就是到了一个地方会有不同的道路…...
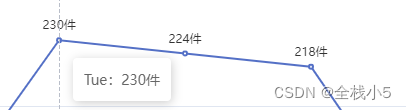
【Echarts】曲线图上方显示数字以及自定义值,标题和副标题居中,鼠标上显示信息以及自定义信息
欢迎来到《小5讲堂》 大家好,我是全栈小5。 这是《前端》系列文章,每篇文章将以博主理解的角度展开讲解, 特别是针对知识点的概念进行叙说,大部分文章将会对这些概念进行实际例子验证,以此达到加深对知识点的理解和掌握…...
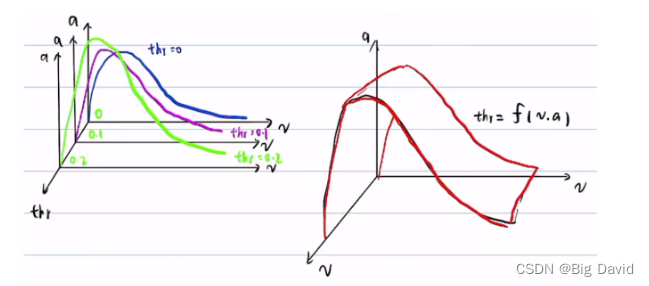
双环PID控制详细讲解
参考博客: (1)PID双环控制(速度环和位置环) (2)PID控制(四)(单环与双环PID) (3)内外双环pid算法 0 单环PID 目标位置→系…...

深入解析Java内存模型
一、背景 并发编程本质问题是:CPU、内存以及IO三者之间的速度差异。CPU速度快于内存、内存访问速度又远远快于IO,根据木桶理论,程序性能取决于最慢的操作,即IO操作。这样会出现CPU和内存交互时,CPU性能无法被充分利用…...

python使用国内镜像源
使用格式 格式为:pip install 库名 -i 镜像地址(注意空格的存在) pip install pandas -i https://pypi.tuna.tsinghua.edu.cn/simple 推荐的镜像源: 清华大学(推荐):https://pypi.tuna.tsing…...
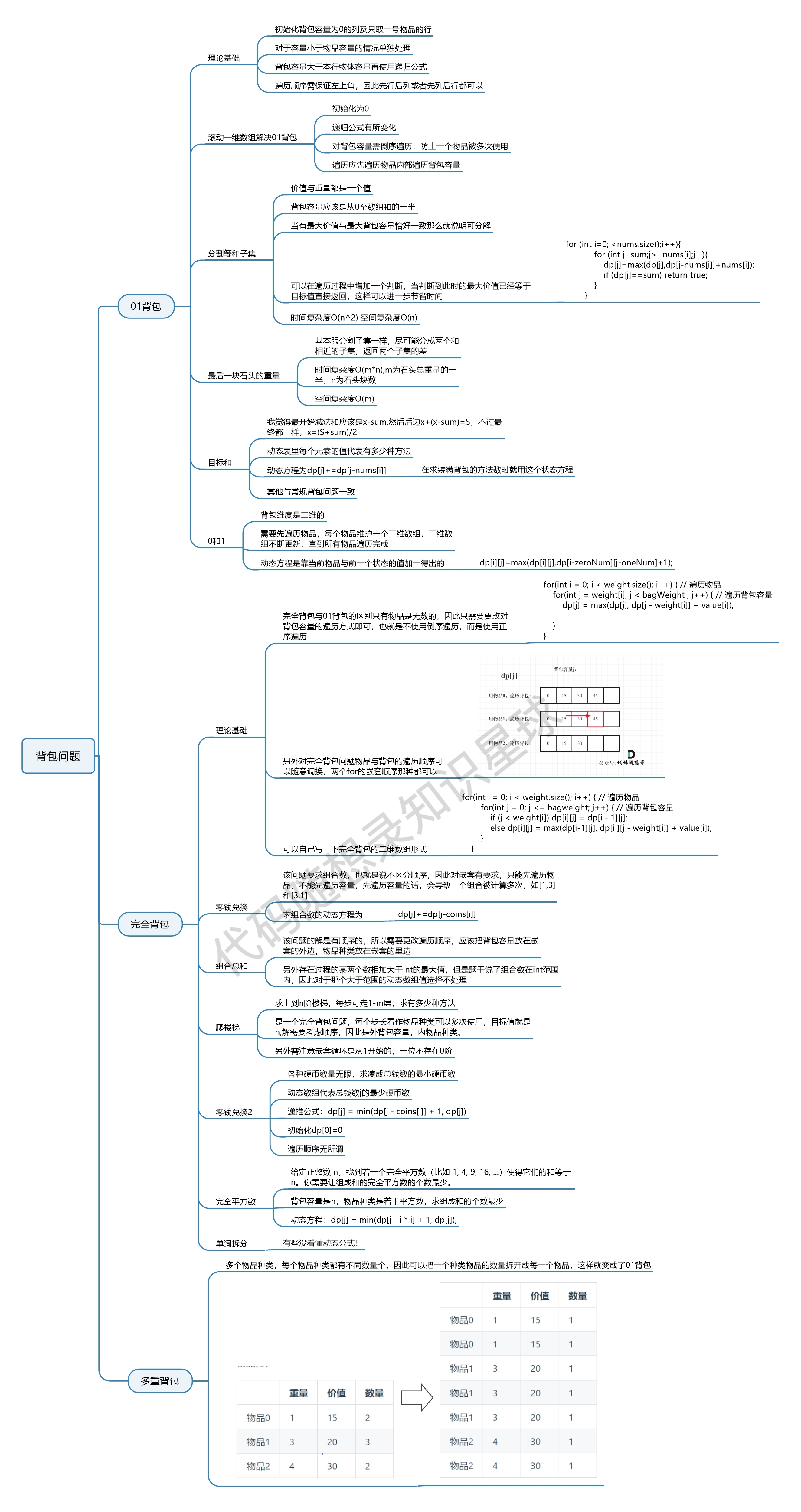
【动态规划】代码随想录算法训练营第四十六天 |139.单词拆分,关于多重背包,你该了解这些! ,背包问题总结篇!(待补充)
139.单词拆分 1、题目链接:. - 力扣(LeetCode) 2、文章讲解:代码随想录 3、题目: 给定一个非空字符串 s 和一个包含非空单词的列表 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词…...
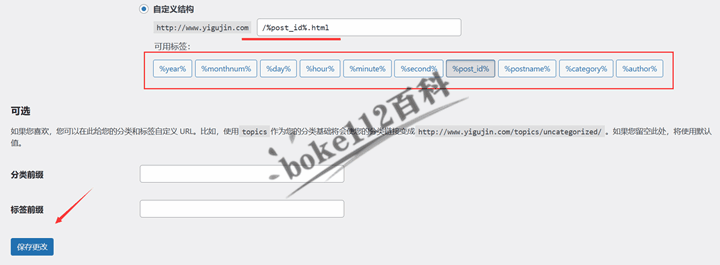
WordPress建站入门教程:如何选择和设置固定链接结构?
我们成功搭建好WordPress网站后,发布的文章对应的URL地址默认是使用“日期和名称型”,即是网站域名跟着的是年月日,最后是文章标题,如http://www.yigujin.com/2024/03/06/免费响应式WordPress博客主题JianYue/ 为了让我们的文章U…...

一款好用的AI工具——边界AICHAT(三)
目录 3.23、文档生成PPT演示3.24、AI文档翻译3.25、AI翻译3.26、论文模式3.27、文章批改3.28、文章纠正3.29、写作助手3.30、文言文翻译3.31、日报周报月报生成器3.32、OCR-DOC办公文档识别3.33、AI真人语音合成3.34、录音音频总结3.35、域方模型市场3.36、模型创建3.37、社区交…...

编程示例: 矩阵的多项式计算以javascript语言为例
编程示例: 矩阵的多项式计算以javascript语言为例 国防工业出版社的《矩阵理论》一书中第一章第8个习题 试计算2*A^8-3*A^5A^4A^2-4I A[[1,0,2],[0,-1,1],[0,1,0]] 代码如下 <html> <head> <title> 矩阵乘法 </title> <script srcset.js ><…...

project generator 简单使用
文章目录 1 progen 资源2 使用简介2.1 安装2.2 添加 target(可选)2.3 替换 CMake 模板(可选)2.4 创建 progen 项目 3 总结 1 progen 资源 0)简介:progen(project-generator,项目生成…...
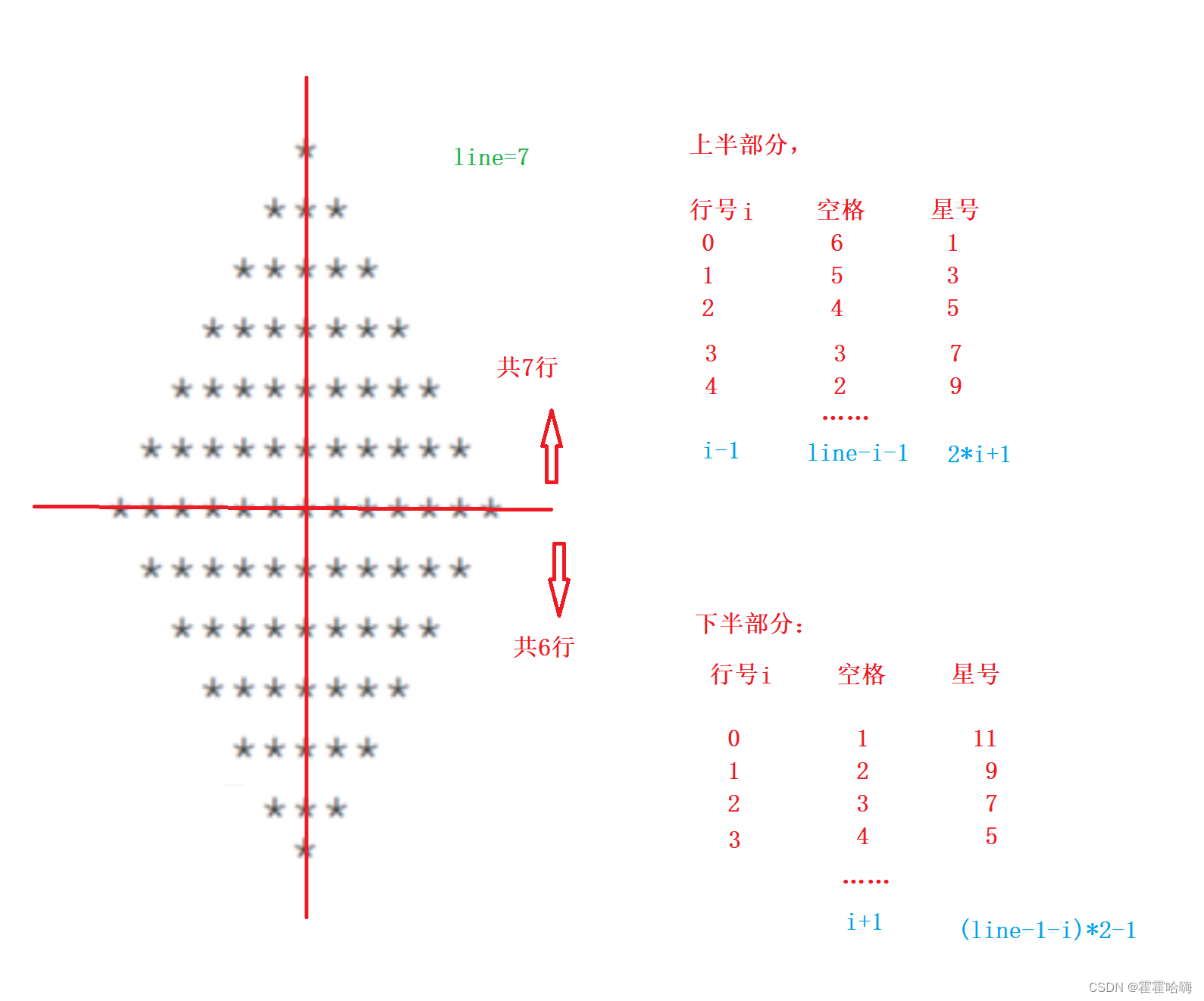
C语言 —— 图形打印
题目1: 思路: 如果我们要打印一个实心正方形,其实就是一个二维数组,i控制行,j控制列,行列不需要控制,arr[i][j]直接打印星号即可。 对于空心正方形,我们只需要控制行和列的条件&…...
常用模块)
Python基础学习(11)常用模块
文章目录 一、time二、random三、os四、sys五、json补充1:JSON字符串补充2:JSON字符串和字典的区别 六、hashlib Python基础学习(1)基本知识 Python基础学习(2)序列类型方法与数据类型转换 Python基础学习(3)进阶字符串(格式化输出) Python基础学习(4)散…...
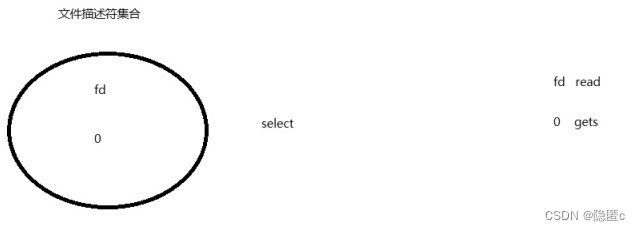
嵌入式学习37-TCP并发模型
TCP并发模型: 1.TCP多线程模型: 缺点: 1.创建线程会带来 资源开销 2.能够实现的 并发量 比较有限 2.IO模型: 1.阻塞IO: 没有…...

C语言字符函数和字符串函数
前言 今天这篇博客咱们一起来认识一些特殊的函数,在编程的过程中,我们经常要处理字符和字符串,为了方便字符和字符串,C语言提供了一些库函数,让我们一起看看这些函数都有什么功能吧!!࿰…...

Go语言必知必会100问题-22 空切片与nil切片有区别吗?
空切片与nil切片有区别吗? 很多开发人员经常混淆nil切片和空切片,不清楚什么时候使用空切片什么时候使用nil,而有些库函数又对这两者使用进行了区分。下面先来看看它们的定义。 空切片是length为0的切片当切片等于nil时为nil切片 下面是几种不同空切片…...
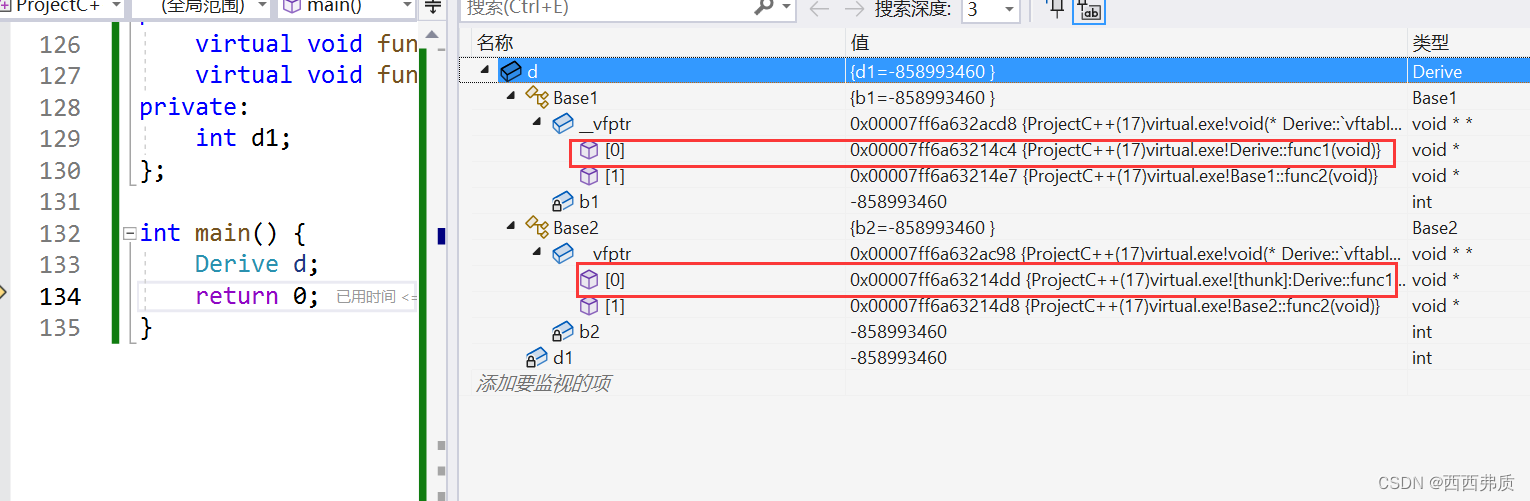
【C++进阶】C++多态概念详解
C多态概念详解 一,多态概念二,多态的定义2.1 多态构成的条件2.2 什么是虚函数2.3 虚函数的重写2.3.1 虚函数重写的特例2.3.2 override和final 2.4 重载和重写(覆盖)和重定义(隐藏)的区别 三,抽象…...
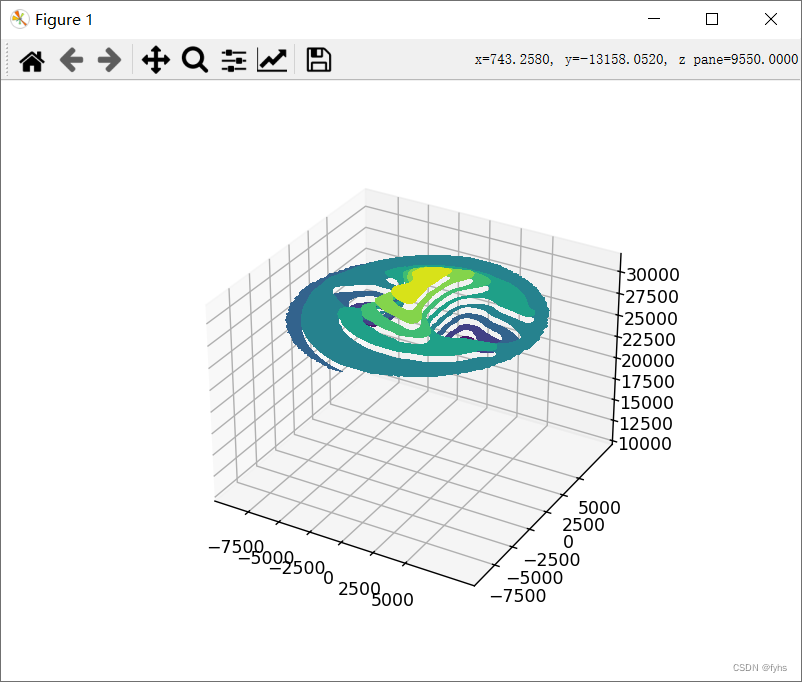
Python 导入Excel三维坐标数据 生成三维曲面地形图(面) 2、线条平滑曲面但有间隔
环境和包: 环境 python:python-3.12.0-amd64包: matplotlib 3.8.2 pandas 2.1.4 openpyxl 3.1.2 scipy 1.12.0 代码: import pandas as pd import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from scipy.interpolate import griddata imp…...
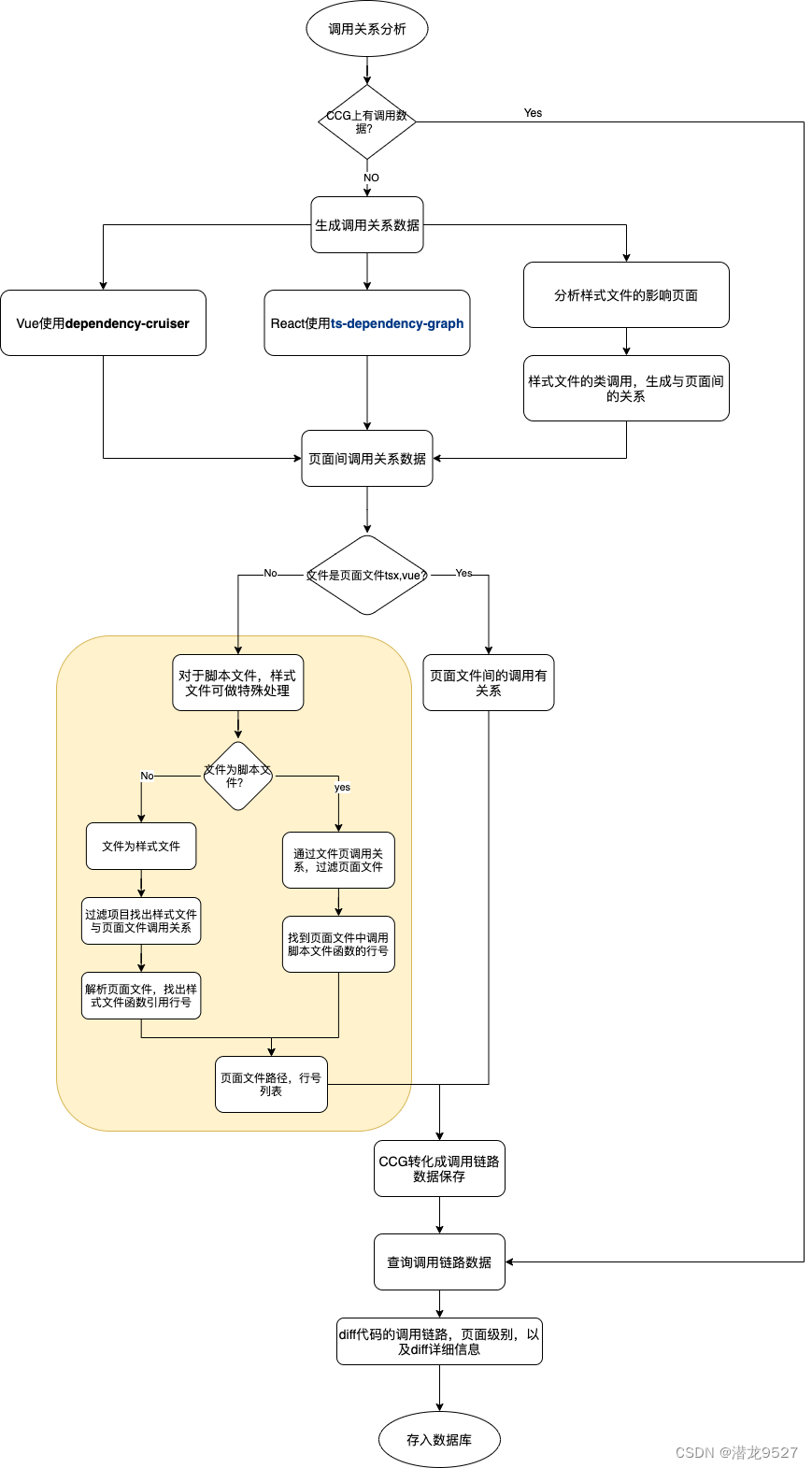
前端精准测试调用链路分析
精准测试在评估需求的测试范围时,需要评估一下代码的影响范围,这个范围有两部分:一是需求直接修改的代码;二是修改代码影响到的功能模块。代码影响到的功能一般是通过调用链路分析来实现的,java和kotlin代码可以由java…...

Objective-C blocks 概要
1.block的使用 1.1什么是block? Blocks是C语言的扩充功能:带有自动变量(局部变量)的匿名函数。 “带有自动变量”在Blocks中表现为“截取自动变量" “匿名函数”就是“不带名称的函数” 块,封装了函数调用及调用…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
