软聚类算法:模糊聚类 (Fuzzy Clustering)
前言
如果你对这篇文章感兴趣,可以点击「【访客必读 - 指引页】一文囊括主页内所有高质量博客」,查看完整博客分类与对应链接。
在介绍模糊聚类之前,我们先简单地列举一下聚类算法的常见分类:
- 硬聚类 (Hard Clustering)
- Connectivity-based clustering (Hierarchical Clustering)
- Centroid-based Clustering (k-means clustering)
- Distribution-based Clustering (Gaussian Mixture Model)
- Density-based Clusterin (DBSCAN)
- 软聚类 (Soft Clustering)
- Fuzzy Clustering
我们之前听说的大部分聚类算法均为硬聚类,即要求每个数据点只能属于一个特定的簇,scikit-learn 中有关于常见硬聚类算法的可视化展示,可供参考:
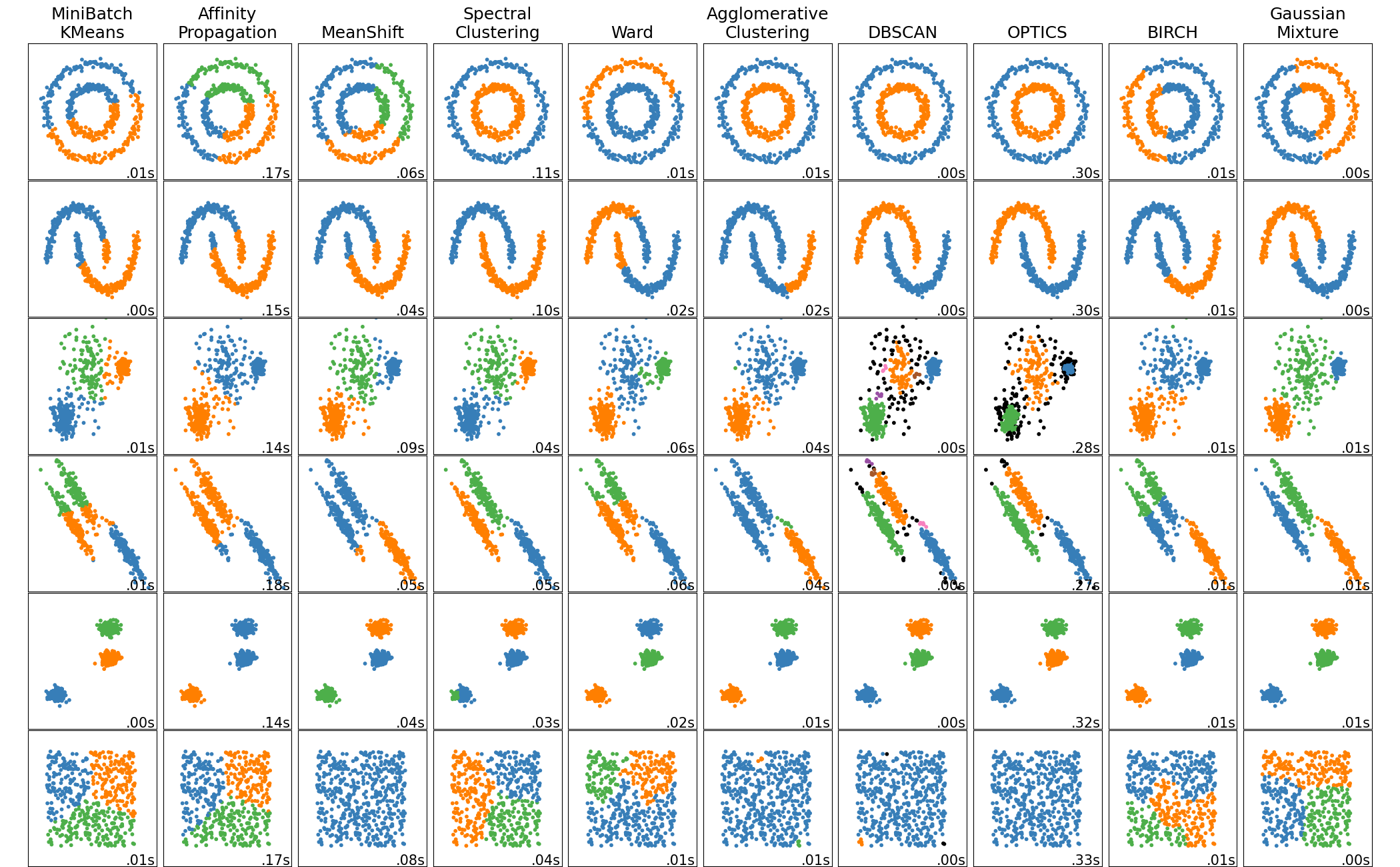
不同于硬聚类,软聚类放松了限制,即允许数据点可以同时属于多个簇。接下来要介绍的模糊聚类即为一种常见的软聚类算法。
模糊聚类
模糊聚类通常用一个向量来表示一个数据点的归属,向量中哪个维度的数值更大,意味着该数据点距离该维度对应簇更近,也可以理解为是归属于该簇的概率越大。
以 Fuzzy c-means (FCM) 聚类算法为例,其过程与 k-means 非常相似:
- 选择 CCC 作为簇个数
- 随机赋予每个点归属于各个簇的概率向量 {wi}i=1N{\{\boldsymbol{w}_i\}}_{i=1}^N{wi}i=1N
- 迭代至收敛
- 重新计算每个簇的簇中心 {ck}k=1C{\{\boldsymbol{c}_k\}}_{k=1}^C{ck}k=1C
- 重新计算每个点归属于各个簇的概率向量 {wi}i=1N{\{\boldsymbol{w}_i\}}_{i=1}^N{wi}i=1N
簇中心 ck\boldsymbol{c}_kck 计算式如下:
ck=∑i=1Nwi,kmxi∑i=1Nwi,km,\boldsymbol{c}_k=\frac{\sum_{i=1}^N w_{i,k}^m \boldsymbol{x}_i}{\sum_{i=1}^N w_{i,k}^m }, ck=∑i=1Nwi,km∑i=1Nwi,kmxi,
其中 m∈(1,∞)m\in (1,\infty)m∈(1,∞) 为超参,控制聚类的模糊程度,其数值越大,聚类结果越模糊,其数组越逼近 111, 其聚类效果越接近 k-means。
数据点 xi\boldsymbol{x}_ixi 的概率向量 wi\boldsymbol{w}_iwi 计算式如下:
wi,k=1∑j=1C(∥xi−ck∥∥xi−cj∥)2m−1,w_{i,k}=\frac{1}{\sum_{j=1}^C \left(\frac{\left\|\boldsymbol{x}_i-\boldsymbol{c}_k\right\|}{\left\|\boldsymbol{x}_i-\boldsymbol{c}_j\right\|}\right)^{\frac{2}{m-1}}}, wi,k=∑j=1C(∥xi−cj∥∥xi−ck∥)m−121,
其满足 ∑k=1Cwi,k=1\sum_{k=1}^C w_{i,k}=1∑k=1Cwi,k=1。FCM 整个聚类过程想要最小化的目标函数如下所示:
J(W,C)=∑i=1N∑k=1Cwi,km∥xi−ck∥2.J(\boldsymbol{W}, \boldsymbol{C})=\sum_{i=1}^N \sum_{k=1}^C w_{i,k}^m\left\|\boldsymbol{x}_i-\boldsymbol{c}_k\right\|^2. J(W,C)=i=1∑Nk=1∑Cwi,km∥xi−ck∥2.
参考资料
- wiki - Fuzzy clustering
- scikit-learn clustering
相关文章:

软聚类算法:模糊聚类 (Fuzzy Clustering)
前言 如果你对这篇文章感兴趣,可以点击「【访客必读 - 指引页】一文囊括主页内所有高质量博客」,查看完整博客分类与对应链接。 在介绍模糊聚类之前,我们先简单地列举一下聚类算法的常见分类: 硬聚类 (Hard Clustering) Connec…...

Java Web 实战 02 - 多线程基础篇(1)
Java Web 实战 02 - 多线程基础篇 - 1一 . 认识线程1.1 概念1.1.1 什么是线程?1.1.2 为什么要有多个线程?1.1.3 进程和线程的区别(面试题)1.2 第一个多线程程序1.3 创建线程1.3.1 继承Thread类1.3.2 实现Runnable接口1.3.3 继承 Thread 类 , 使用匿名内部类1.3.4 实现 Runnab…...
C/C++开发,无可避免的多线程(篇三).协程及其支持库
一、c20的协程概念 在c20标准后,在一些函数中看到co_await、co_yield、co_return这些关键词,这是c20为协程实现设计的运算符。 协程是能暂停执行以在之后恢复的函数。原来我们调用一个功能函数时,只要调用了以后,就要完整执行完该…...
原创论文项目背景合集)
高级信息系统项目管理(高项 软考)原创论文项目背景合集
以下为原创的高项论文项目背景合集5篇,建议自己以此为基础,再多多打磨完善一下,避免雷同,同时使项目背景更加真实可信。 一、某市智慧工地系统建设项目 某市住建局智慧工地系统建设项目是在该市住建局促进建筑行业转型升级和科技创新,强化工程质量安全,推动建筑业高质量…...

锁屏面试题百日百刷-Hive篇(十一)
锁屏面试题百日百刷,每个工作日坚持更新面试题。锁屏面试题app、小程序现已上线,官网地址:https://www.demosoftware.cn。已收录了每日更新的面试题的所有内容,还包含特色的解锁屏幕复习面试题、每日编程题目邮件推送等功能。让你…...

一看就懂,等保2.0工作流程这么做
等保2.0相关国家标准于2019年12月1日开始实施,标志着我国网络安全等级保护工作进入一个崭新的阶段,对于加强我国网络安全保障工作,提升网络安全保护能力具有十分重要的意义。很多行业主管单位要求行业客户开展等级保护工作,合理地…...
Kerberos 域委派攻击之非约束性委派
CSDN文章自动迁移自博客在Windows 2000 Server 首次发布 Active Directory 时,Microsoft 必须提供一种简单的机制来支持用户通过 Kerberos 向 Web Server 进行身份验证并需要代表该用户更新后端数据库服务器上的记录的方案。这通常称为“Kerberos 双跳问题”&#x…...
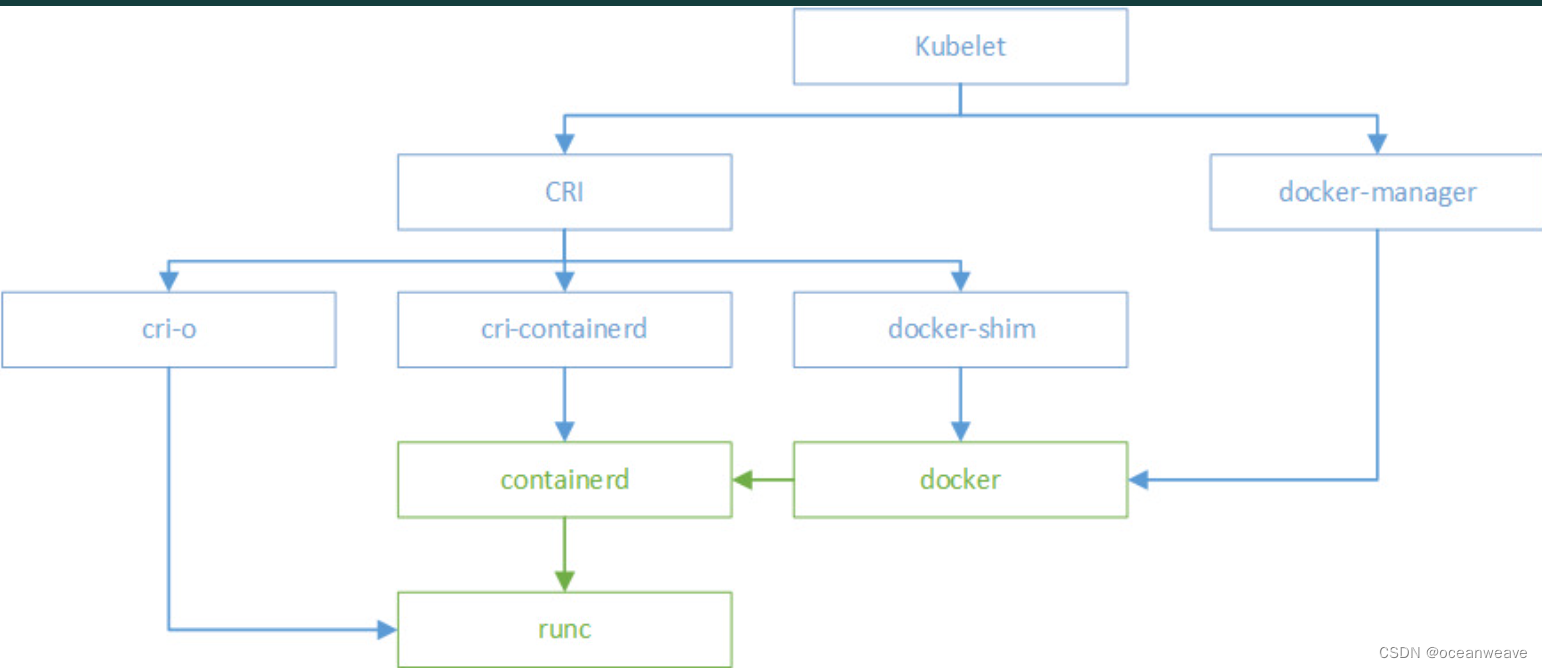
【容器运行时】一文理解 OCI、runc、containerd、docker、shim进程、cri、kubelet 之间的关系
参考 docker,containerd,runc,docker-shim 之间的关系Containerd shim 进程 PPID 之谜内核大神教你从 Linux 进程的角度看 DockerRunC 简介OCI和runCContainerd 简介从 docker 到 runCDockershim究竟是什么技术干货|Docker和 Con…...
spark兼容性验证
前言 Apache Spark是专门为大规模数据处理而设计的快速通用的计算引擎,Spark拥有Hadoop MapReduce所具有的优点,但不同于Mapreduce的是Job中间输出结果可以保存在内存中,从而不再需要读写HDFS,因此Spark能更好的适用于数据挖掘与…...

docker逃逸复现--pid=host模式下的逃逸
漏洞原理当docker以--pidhost模式启动时,你可以通过在容器进程中注入一些shellcode进行逃逸。相当于给了docker Linux中的CAP_SYS_PTRACE权限--pidhost:意味着宿主机与容器公享一套pid,如此做容器就可以访问并跟踪宿主机的进程Linux中的CAP_S…...

【环境配置】Windows系统下搭建Pytorch框架
【环境配置】Windows系统下搭建Pytorch框架 在Windows Serve 2019系统下搭建Pytorch框架 目录 【环境配置】Windows系统下搭建Pytorch框架1.用驱动总裁安装显卡驱动2.在cmd运行nvidia-smi3.安装cuda4.安装cudnn5.安装pytorch的命令1.首次安装2.操作失误需要重新安装6.安装torc…...
Dockerfile简单使用入门
什么是 Dockerfile? Dockerfile 是一个用来构建镜像的文本文件,文本内容包含了一条条构建镜像所需的指令和说明。 docker build命令用于从Dockerfile构建映像。可以在docker build命令中使用-f标志指向文件系统中任何位置的Dockerfile。 例如࿱…...

什么是CCC认证3C强制认证机构
什么是CCC认证3C强制认证机构? 3C认证的全称为“强迫性产物认证轨制”,它是中国政府为掩护消费者人身平安和国度平安、增强产物品质治理、按照法律法规履行的一种产物及格评定轨制。所谓3C认证,便是中国强迫性产物认证轨制,英文名…...

C语言-基础了解-18-C共用体
C共用体 一、共用体 共用体是一种特殊的数据类型,允许您在相同的内存位置存储不同的数据类型。您可以定义一个带有多成员的共用体,但是任何时候只能有一个成员带有值。共用体提供了一种使用相同的内存位置的有效方式 二、定义共同体 为了定义共用体&…...
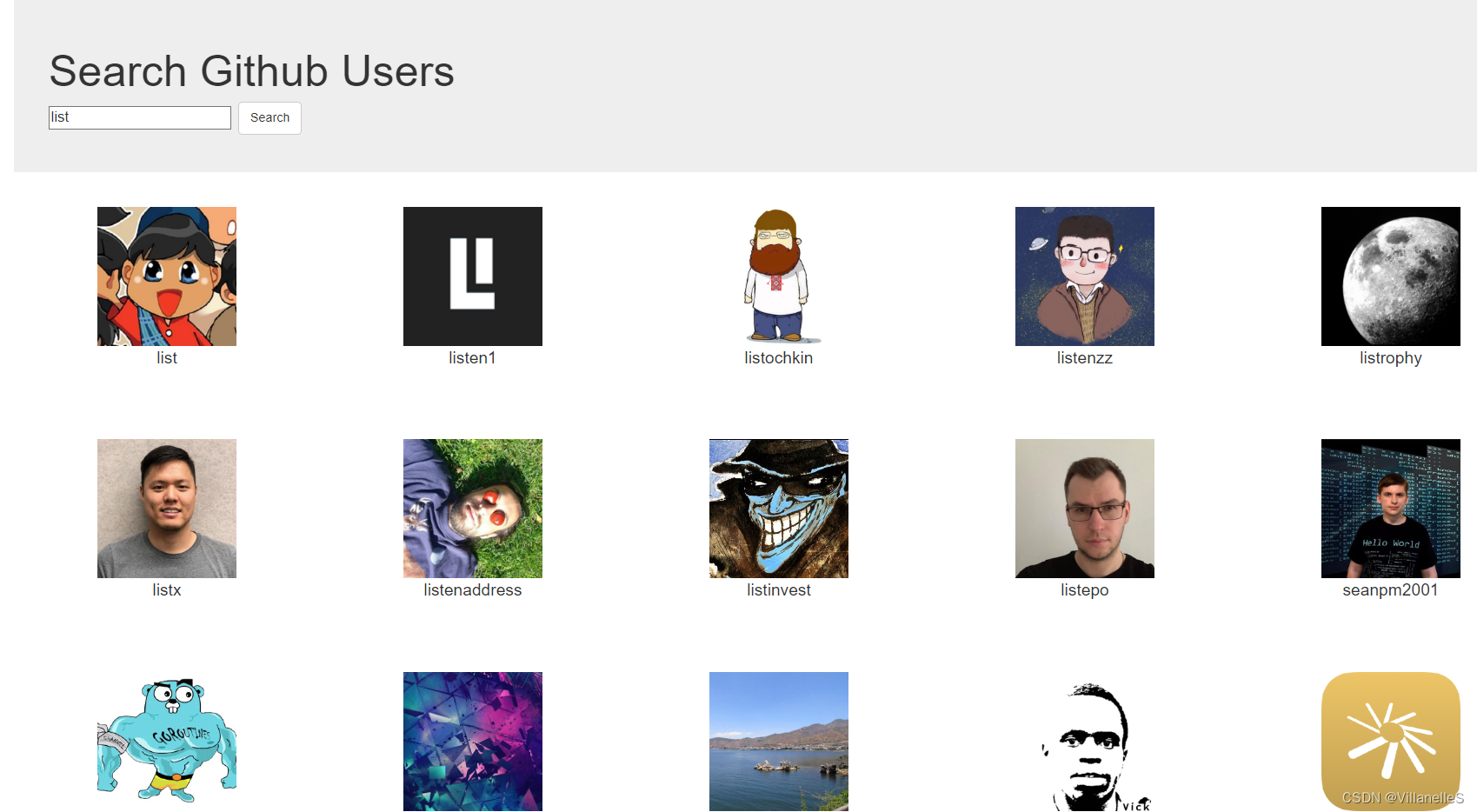
Vue基础18之github案例、vue-resource
Vue基础18github案例静态页面第三方样式引入(以bootstrap举例)App.vueSearch.vueList.vue列表展示接口地址使用全局事件总线进行兄弟间组件通信Search.vueList.vue完善案例List.vueSearch.vue补充知识点:{...this.info,...this.dataObj}效果呈…...
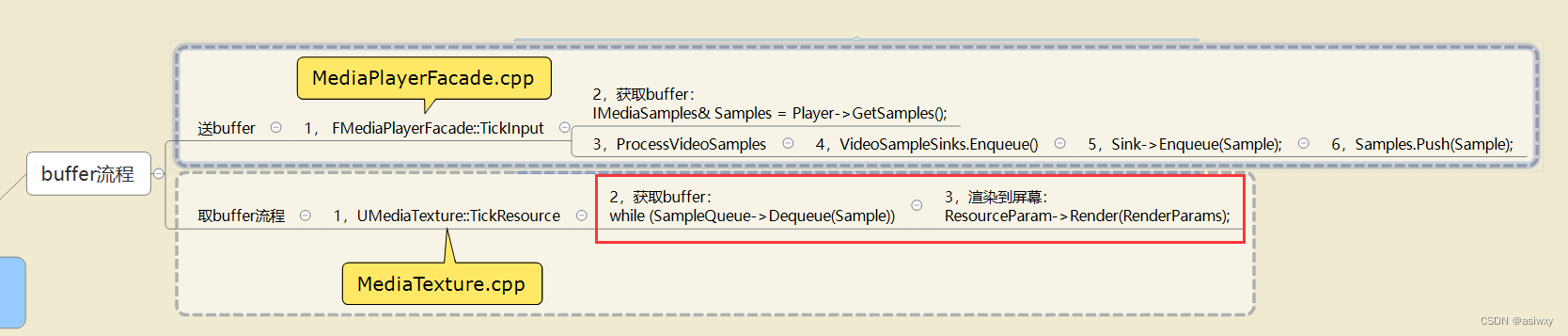
UE4 c++ Mediaplayer取消自动播放,运行时首帧为黑屏的问题
0,前言 工作需要使用C制作一个ue4的视频插件,其中一个功能是能够选择 运行时是否自动播放 视频的功能。 在实现时遇见了一个问题,取消自动播放之后,运行时首帧是没有取到的,在场景里面看是黑色的。就这个问题我想到了使…...

C语言-基础了解-17-C结构体
C结构体一、c结构体C 数组允许定义可存储相同类型数据项的变量,结构是 C 编程中另一种用户自定义的可用的数据类型,它允许您存储不同类型的数据项。结构体中的数据成员可以是基本数据类型(如 int、float、char 等),也可…...
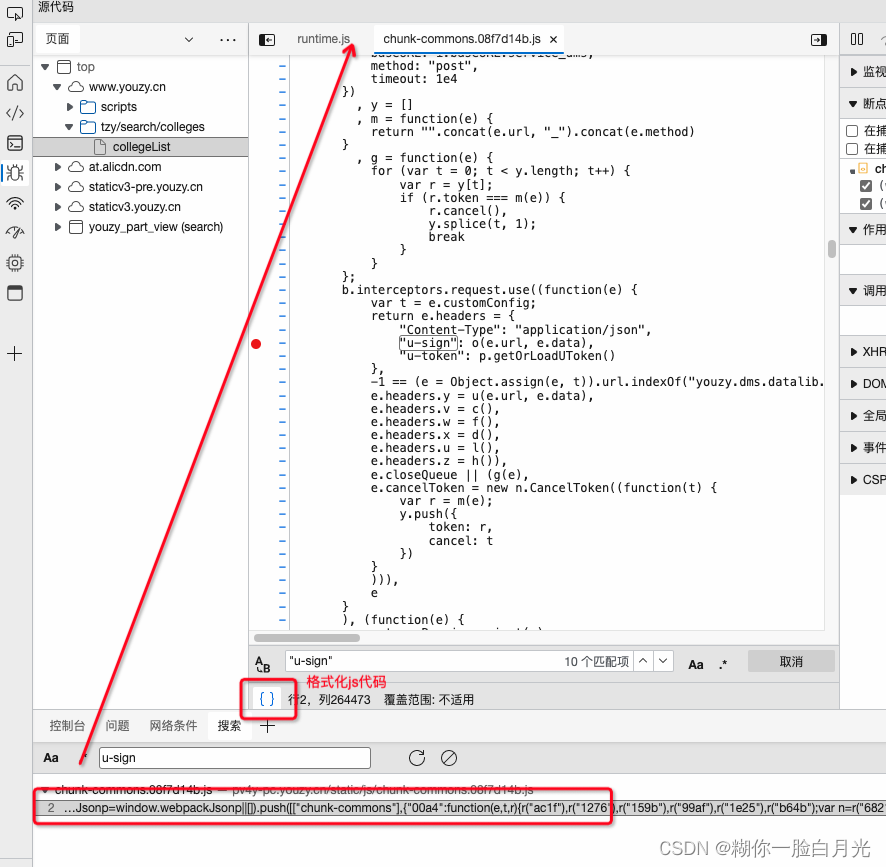
Python爬虫实践:优志愿 院校列表
https://www.youzy.cn/tzy/search/colleges/collegeList获取目标网址等信息打开开发人员工具(F12),拿到调用接口的地址,以及接口请求参数等信息,如下curl https://uwf7de983aad7a717eb.youzy.cn/youzy.dms.basiclib.ap…...

Java框架学习 | MySQL和Maven笔记
1.MySQL提问式思考 为什么要有数据库?MySQL的优劣势?Java的优劣势? JavaMySQL开源具有大量的社区成员和丰富的资源免费/具有大量的社区成员和丰富的资源可扩展性多态、继承和接口等分区、复制和集群等方式扩展数据库的容量和性能安全性有许…...

C++入门教程||C++ 变量作用域||C++ 常量
C 变量作用域 作用域是程序的一个区域,一般来说有三个地方可以声明变量: 在函数或一个代码块内部声明的变量,称为局部变量。在函数参数的定义中声明的变量,称为形式参数。在所有函数外部声明的变量,称为全局变量。 我…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
