【C语言步行梯】自定义函数、函数递归详谈

🎯每日努力一点点,技术进步看得见
🏠专栏介绍:【C语言步行梯】专栏用于介绍C语言相关内容,每篇文章将通过图片+代码片段+网络相关题目的方式编写,欢迎订阅~~
文章目录
- 什么是函数
- 库函数
- 自定义函数
- 函数执行示例
- 函数的参数
- 函数的调用
- 函数的嵌套调用和链式访问
- 函数的定义和声明
- 函数递归
什么是函数
数学中我们常见到函数的概念。但是你了解C语言中的函数吗?C语言中的函数可不是数学上的表达式,咱一起来看看它究竟是什么<( ̄︶ ̄)↗[GO!]
我们知道,原材料进入工厂后,之后就会有产品产出。函数就像是工厂一样,我们将没有处理过的数据放进去,它就会返回给我需要的结果。

在维基百科中,将函数解释为子程序。因为函数具有独立处理数据或实现一部分功能的能力。下面我们来看一下比较官方的解释:
在计算机科学中,子程序是一个大型程序中的某部分代码, 由一个或多个语句块组成。它负责完成某项特定任务,而且相较于其他代码,具备相对的独立性。一般会有输入参数并有返回值,提供对过程的封装和细节的隐藏。这些代码通常被集成为软件库。
库函数
在C语言中,函数分为自定义函数和库函数。自定义函数就是程序员需要自行实现的函数,而库函数是C语言库中自带的,我们可以在包含对应头文件的情况下使用。
既然程序员可以自行编写函数,那为什么会有库函数?

在我们刚开始学习C语言时,迫不及待地在屏幕上打印"Hello World"。这时我们调用了printf函数,并且是在包含了stdio头文件的前提下。其实,printf已经在stdio头文件编写好了,我们需要时可以随时调用。
我们先来介绍一些常用的库函数吧。首先看看pow函数,它用于计算n的k次方,第一个传入的参数是底数,第二个传入的参数是指数。例如:计算 2 8 2^8 28就可以用pow(2,8)。
#include <stdio.h>
#include <math.h>//调用pow函数需要包含math头文件int main()
{printf("%d\n", pow(2, 8));return 0;
}
再来介绍一个求字符串长度的函数strlen,只要将字符串传入,它就会将字符串长度返回。
#include <stdio.h>
#include <string.h>//调用strlen函数需要包含string头文件int main()
{printf("%d\n", strlen("Jammingpro"));
}
最后,我们介绍一下字符串拷贝函数strcpy。如果我们要将str1中的字符拷贝到str2中,则可以使用strcpy(str2, str1)。
#include <stdio.h>
#include <string.h>int main()
{char str1[] = "Jammingpro";char str2[] = "xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx";strcpy(str2, str1);printf("%s\n", str2);return 0;
}
★ps:字符串在存储时,最后一个位置会以\0结束,表示字符串结束。strcpy在拷贝时,会将被拷贝字符串的\0字符一并拷贝下来。
现在,我们就能知道为什么要有库函数了。像上面我们描述的基础功能,它们不是业务性的代码。我们在开发的过程中每个程序员都可能用的到,为了支持可移植性和提高程序的效率,所以C语言的基础库中提供了一系列类似的库函数,方便程序员进行软件开发。
当然,C语言中有那么多的库函数,我们不可能记得牢固,在需要的时候我们可以上官方文档查询→C语言库函数查询通道
自定义函数
如果库函数能干所有的事情,那还要程序员干什么?所有更加重要的是自定义函数。
自定义函数和库函数一样,有函数名,返回值类型和函数参数。 但是不一样的是这些都是我们自己来设计。这给程序员一个很大的发挥空间。下面我们看一看函数的组成↓↓↓
ret_type func_name(para1,...)
{statement;//语句项
}
//ret_type --> 返回值类型
//func_name --> 函数名称
//para1 --> 函数参数
函数执行示例
我们先看一个例子吧,下面代码的get_max用于获取两个数中的较大值↓↓↓
#include <stdio.h>int get_max(int num1, int num2)
{return (num1 > num2 ? num1 : num2);
}int main()
{int m = 0;int n = 0;scanf("%d %d", &m, &n);printf("较大值是:%d\n", get_max(m, n));
}
看完这段代码,可能还是不大理解它的执行流程。下面我通过图片+文字解释的方式模拟程序执行流程。
程序从main函数依次向下执行,如图所示,执行1、2、3号语句。当执行到printf函数所在行时,因为调用了get_max函数,此时程序跳转到get_max代码所在位置执行,执行完毕后,将计算结果返回给调用位置。此时,printf再打印出最大值。

函数的参数
在上面的代码中,我们看到printf中的get_max()中有两个参数,分别是m和n。而main函数上方的get_max函数中也有两个参数,即num1和num2。下面我们来聊聊这两个地方的参数有什么不同,再聊聊程序调用函数时内存的变化。
★ps:程序在执行过程中,会将函数信息、变量等保存在栈中。栈保存数据从高地址向低地址处保存。栈有后进先出的特点,后放进去的数据要先取出来,才能取其他数据。
①函数执行到main函数时,会将main函数信息入栈(入栈就是保存到栈空间的意思),如下图所示。

②执行m和n的定义语句后,会先后在栈中开辟一个空间,用于保存m和n的数值。

③执行scanf语句读取用户输入,保存到m和n所在地址。这里假设输入的数值是8和5。
★ps:&是取地址运算符

④执行printf时遇到了get_max函数,此时调用get_max函数,则需要将该函数的信息先入栈。将m的值传递给num1时,此时num1入栈,并初始化为8;将n的值传递给num2时,此时num2入栈,并初始化为5。

⑤在get_max函数执行完毕后,num2、num1、get_max依次出栈(出栈就是从栈空间删除的意思)。在整个程序执行完毕,n、m、main函数依次出栈。
这里的m和n是实参,它们是在函数调用前已经存在的变量。而num1、num2称为形参,它们是在函数调用时才开辟空间的变量。下面看一下实参和形参的具体定义:
实际参数(实参):
真实传给函数的参数,叫实参。实参可以是:常量、变量、表达式、函数等。无论实参是何种类
型的量,在进行函数调用时,它们都必须有确定的值,以便把这些值传送给形参。
形式参数(形参):
形式参数是指函数名后括号中的变量,因为形式参数只有在函数被调用的过程中才实例化(分配
内存单元),所以叫形式参数。形式参数当函数调用完成之后就自动销毁了。因此形式参数只在
函数中有效。
现在我有个想法,我想实现一个交换两个数数值的函数,你来判断一下,下面的代码能否实现交换两个数值的效果。
#include <stdio.h>
void Swap(int num1, int num2)
{int tmp = num1;num1 = num2;num2 = tmp;
}
int main()
{int m = 5;int n = 6;printf("交换前,m = %d, n = %d\n",m, n);Swap(m, n);printf("交换后,m = %d, n = %d\n", m, n);return 0;
}
这段代码无法实现m和n的数值交换。因为m和n传递给num1和num2时,num1和num2开辟了新的空间,num1和num2的交换并不会影响m和n。两者存放的位置都不一样,不会互相影响的。
如果我们真的想实现两个数的数值交换,则调用函数时,函数中交换的必须是主函数中的m和n,而不能再另外开辟空间。咱们来看一下新的代码↓↓↓
#include <stdio.h>
void Swap(int* pm, int* pn)
{int tmp = *pm;*pm = *pn;*pn = tmp;
}
int main()
{int m = 5;int n = 6;printf("交换前,m = %d, n = %d\n",m, n);Swap(&m, &n);printf("交换后,m = %d, n = %d\n", m, n);return 0;
}
这段代码,在调用函数时,将m和n的地址传递给get_max函数,get_max函数中使用指针进行接收。在m和n存储位置上的交换操作就能真正交换m和n的数值了。
函数的调用
传值调用
函数的形参和实参分别占有不同内存块,对形参的修改不会影响实参。
传址调用
传址调用是把函数外部创建变量的内存地址传递给函数参数的一种调用函数的方式。
这种传参方式可以让函数和函数外边的变量建立起正真的联系,也就是函数内部可以直接操作函数外部的变量。
学习完上面的内容,先让我们应用一下吧。

test1:写一个函数判断是不是闰年
#include <stdio.h>int is_leap_year(int year)
{return ((year % 4 == 0 && year % 100 != 0) || (year % 400 == 0));
}int main()
{int year = 0;scanf("%d", &year);if(is_leap_year(year))printf("是闰年\n");elseprintf("不是闰年\n");return 0;
}
★ps:闰年满足如下条件中的一个:①能被4整除,且不能被100整除;②能被400整除。
test2:写一个函数,每调用一次这个函数,num的数值就会+1
#include <stdio.h>int add_1(int num)
{return num + 1;
}int main()
{int num = 0;num = add_1(num);printf("%d\n", num);return 0;
}
函数的嵌套调用和链式访问
嵌套调用
嵌套调用是指,一个函数中调用了另一个函数。我们来看一个例子,你就会知道了↓↓↓
#include <stdio.h>void sayHi()
{printf("Hi!\n");
}void introduc()
{printf("starting....\n");sayHi();
}int main()
{introduc();return 0;
}
上面代码中introduc函数中被调用后,它又调用了sayHi函数。像这种在一个函数中调用另一个函数的情况,就称为函数的嵌套调用。
链式调用
关于链式调用,我还是需要一个例子来解释。↓↓↓
★ps:printf函数的返回值是它在屏幕上打印的字符个数
#include <stdio.h>
int main()
{printf("%d ", printf("%d ", printf("%d ", 43)));return 0;
}
像上面的代码中,调用printf("%d “,43)的返回值作为下一个printf函数的参数的情况,称为链式调用。这里用图片解释一下这个代码的执行过程↓↓↓

先执行printf(”%d ",43),在屏幕上打印"43 "(最后有一个空格),一共3个字符,所以它的返回值为3。在执行绿色框的printf时,它打印"3 ",一共2个字符,所以它的返回值为2。在执行最外围的printf时,它打印"2 “。所以最后打印出"43 3 2”。
函数的定义和声明
首先让我们谈一谈函数的定义,函数的定义就是给出函数的名称、参数、返回值,并且给出函数体,给出函数的具体实现。下面给出函数定义的具体描述:
函数定义
函数的定义是指函数的具体实现,交待函数的功能实现。
例如,下面的Add函数就是函数定义,因为它给出了Add函数具体是怎么实现的。
int Add(int a, int b)
{return a + b;
}
上面给出的各个例子中,我都会将自定义函数放在main函数之前。因为编译器在处理代码时是从上到下的。假如我们将自定义函数放在main函数的后面,若此时main函数中调用了自定义函数,编译器此时并不认识,因为它还没读到,此时编译器将会报错。下图中,蓝色部分是编译器已经读到的部分,因为get_max函数编译器还没读到,当读到调用get_max函数时就会报错。

为了避免编译器报错,我们可以在main函数前给出函数的声明,即使函数定义在main函数后,也不用担心了。
#include <stdio.h>int get_max(int num1, int num2);//我就是函数的声明
//int get_max(int, int); -->写成这样也可以,参数名可以省略int main()
{int m = 0;int n = 0;scanf("%d %d", &m, &n);printf("较大值是:%d\n", get_max(m, n));
}int get_max(int num1, int num2)
{return (num1 > num2 ? num1 : num2);
}
下面我们来看一下关于函数声明的定义和注意事项:
函数声明
- 告诉编译器有一个函数叫什么,参数是什么,返回类型是什么。但是具体是不是存在,无关
紧要。 - 函数的声明一般出现在函数的使用之前。要满足先声明后使用。
- 函数的声明一般要放在头文件中的。
关于上面的第3条,我来解释解释吧。在实际开发过程中,一个项目需要很多程序员开发,大家不可能同时在一个源文件中编写代码。此时,我们可以先在后缀为.h的头文件中给出各个函数的声明,在函数的定义的文件中包含这个头文件,在调用这些函数的主函数所在文件也包含这个头文件就可以了。
★ps:包含C语言库的头文件使用#include<头文件名.h>,调用自定义的头文件,使用`#include “头文件名.h”
下面就是一个分文件编写的示例。max.h中保存的是函数的声明,mac.c保存的是函数的定义。在编译器读取前main.c时,#include max.h语句会将max.h中的函数声明文本替换到main.c中,当执行到get_max时,编译器会自动跳转到max.c中指定对应的函数。

函数递归
什么是递归呢?先来看一下递归的定义↓↓↓
程序调用自身的编程技巧称为递归。 递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。 递归的主要思考方式在于:把大事化小
递归的两个必要条件
- 存在限制条件,当满足这个限制条件的时候,递归便不再继续。
- 每次递归调用之后越来越接近这个限制条件。
上面我们介绍了,函数调用会将函数的相关信息保存到栈中,如果无限递归,则栈会被装满,此时就会报错。
上面这堆关于递归的解释还是让人头大,下面给些例子+图形解释,来理解一下函数递归吧。

下面代码使用函数递归,求解n!(n的阶乘)。
#include <stdio.h>int cal(int n)
{if(n <= 1) return 1;else return cal(n - 1) * n;
}int main()
{int n = 0;scanf("%d", &n);printf("%d! = %d",n ,cal(n));return 0;
}
以n=4为例,我们来看一下函数递归的执行过程。main函数指定到printf时,调用了cal(4)。下面给出cal(4)的执行步骤:
①cal(4)被调用
②4 <= 1不满足,执行else分支,即return cal(n-1)*n --> cal(3) * 4
③cal(3)被调用,3 <= 1不满足,执行else分支,即return cal(n-1)*n --> cal(2)*3
④cal(2)被调用,2 <= 1不满足,执行else分支,即return cal(n-1)*n --> cal(1)*2
⑤cal(1)被调用,1 <= 1满足,返回1
⑥cal(2)的return语句返回cal(1)2,即返回12
⑦cal(3)的return语句返回cal(2)3,即返回23
⑧cal(4)的return语句返回cal(3)4,即返回64给调用处

下面再出一个递归示例:接收一个整型数,打印它的每一位。例如:123,打印"1 2 3"。
#include <stdio.h>
void printNum(int n)
{if(n > 9)printNum(n / 10);printf("%d ", n % 10);
}int main()
{int n = 0;scanf("%d", &n);printNum(n);return 0;
}
以123为例,借助图解释这段代码的递归过程。
①调用printNum(123)。printNum(123)执行,if语句判断条件成立调用printNum(123 / 10),即调用printNum(12)
②printNum(12)执行,if语句判断条件成立调用printNum(12 / 10),即调用printNum(1)
③printNum(1)执行,if语句判断条件不成立,打印1后返回
④返回printNum(12),向下打印2后返回
⑤返回printNum(123),向下打印3后返回函数调用处

经过上面的介绍,对函数递归有了大致的了解了!在介绍函数调用时,我们讲到了,函数调用时需要保存函数的信息(也称为建立栈帧)。如果递归的层数过多,则时空效率过低。
下面我们通过一个例子来讲解递归存在的问题,同时比较一下迭代相比递归的优势。下面是一个以递归形式实现的求解斐波那契数列的代码↓↓↓
#include <stdio.h>long long fib(n)
{if(n <= 2) return 1;else return fib(n - 1) + fib(n - 2);
}int main()
{int n = 0;scanf("%d", &n);printf("第n项为:%d\n", fib(n));
}
以fib(50)为例,它的执行过程如下所示。我们可以发现fib(46)等被多次计算,这导致了大量的时间和空间的浪费。

我们可以通过执行下面代码,得出在计算fib(50)时,重复计算fib(3)多少次,这将会是一个很大的数字。
#include <stdio.h>int count = 0;long long fib(n)
{if(n == 3) count++;if(n <= 2) return 1;else return fib(n - 1) + fib(n - 2);
}int main()
{int n = 0;scanf("%d", &n);fib(50);printf("%d\n", count);return 0;
}
在调试 fib 函数的时候,如果你的参数比较大,那就会报错: `stack overflow(栈溢出) 这样的信息。 系统分配给程序的栈空间是有限的,但是如果出现了死循环,或者(死递归),这样有可能导致一直开辟栈空间,最终产生栈空间耗尽的情况,这样的现象我们称为栈溢出。
该如何解决上面的问题呢?
- 将递归改写成非递归。
- 使用static对象替代nonstatic局部对象。在递归函数设计中,可以使用static对象替代nonstatic局部对象(即栈对象),这不仅可以减少每次递归调用和返回时产生和释放nonstatic对象的开销,而且static对象还可以保存递归调用的中间状态,并且可为各个调用层所访问。
咱们再来看看迭代法(非递归)实现斐波那契数列↓↓↓
#include <stdio.h>int fib(int n)
{int a = 1;int b = 1;int c = 1;for(int i = 2; i < n; i++){c = a + b;a = b;b = c;}return c;
}int main()
{int n = 0;scanf("%d", &n);printf("%d\n", fib(n));return 0;
}
相比于递归的重复计算,迭代法并不会出现。将两份代码放Visual Studio执行fib(50),会发现迭代法许久都出不来结果。
★ps:
- 许多问题是以递归的形式进行解释的,这只是因为它比非递归的形式更为清晰。
- 但是这些问题的迭代实现往往比递归实现效率更高,虽然代码的可读性稍微差些。
- 当一个问题相当复杂,难以用迭代实现时,此时递归实现的简洁性便可以补偿它所带来的运行时开销。
下面我们用牛刀小试一下:
小明每次可以向上爬一阶或者两阶楼梯,现输入台阶的阶数,请输入爬到楼顶的方法数。例如:3阶台阶的方法数为3;4阶台阶的方法数为5。
#include <stdio.h>int climb(int n)
{if(n <= 1) return 1;else return climb(n - 1) + climb(n - 2);
}int main()
{int stair = 0;scanf("%d", &stair);printf("%d\n", climb(stair));return 0;
}
爬到第n阶台阶,可以是从n-1号台阶爬1阶到达,也可以是从n-2号台阶爬2阶到达。由此可以到climb(n) = climb(n - 1) + climb(n - 2)。这道题是一个递归可实现的问题,也可以用动态规划的方法(迭代的方式)实现哦!
🚩这篇文章结束了~~
如果文章中出现了错误,欢迎私信或留言。(๑•̀ㅂ•́)و✧
有任何疑问请评论或私信哦~~o( ̄▽ ̄)ブ
相关文章:

【C语言步行梯】自定义函数、函数递归详谈
🎯每日努力一点点,技术进步看得见 🏠专栏介绍:【C语言步行梯】专栏用于介绍C语言相关内容,每篇文章将通过图片代码片段网络相关题目的方式编写,欢迎订阅~~ 文章目录 什么是函数库函数自定义函数函数执行示例…...

小米汽车上市进入倒计时,已开启内部试驾
在十四届全国人大二次会议上,全国人大代表、小米集团创始人、董事长CEO雷军回应了小米汽车的最新消息,小米汽车预计很快就要正式上市。 小米汽车推出了两款车型:SU7和SU7 Max。这两款车型均为纯电轿车,带来了不同的配置和性能特点…...

React render方法的原理?在什么时候会被触发?
一、原理 首先,render函数在react中有两种形式: 在类组件中,指的是render方法: class Foo extends React.Component {render() {return <div> Foo </div>;} } 在函数组件中,指的是函数组件本身&#x…...

打卡学习kubernetes——了解kubernetes组成及架构
目录 1 什么是kubernetes 2 kubernetes组件 3 kubernetes架构 1 什么是kubernetes kubernetes是一个旨在自动部署、扩展和运行应用容器的开源平台。目标是构建一个生态系统,提供组件和工具以减轻在公共和私有云中运行应用程序的负担。 kubernetes是:…...

python(ogr)处理geojson为本地shp文件
前言 本次所利用的geojson数据来自https://geo.datav.aliyun.com/areas_v3/bound/410000_full.json ,如果觉得下方代码看起来不方便,可以来GitHub上来看,在这上面还有一些辅助内容便于理解 GISpjd/GIS-union-Python (github.com)https://gi…...
Docker容器化技术(使用Dockerfile制作镜像)
Docker中的镜像分层 Docker 支持通过扩展现有镜像,创建新的镜像。实际上,Docker Hub 中 99% 的镜像都是通过在 base 镜像中安装和配置需要的软件构建出来的。 1、Docker 镜像为什么分层 镜像分层最大的一个好处就是共享资源。 比如说有多个镜像都从相…...

C++ struct 结构体类型
在处理大批量数据时,一般会使用数组来实现,数组中各元素都属于同一数据类型。但在实际问题中,要处理的一组数据往往具有不同的数据类型。如一个学生的个人信息有学号(num)、姓名(name)、性别&am…...

什么是VR虚拟现实体验店|VR主题馆加盟|元宇宙文化旅游
VR虚拟现实体验店是一种提供虚拟现实技术体验的场所。在这样的店铺里,顾客可以通过专业的设备和技术,体验虚拟现实技术带来的沉浸式感觉。 通常,这些商店提供一系列VR体验,包括互动游戏、沉浸式模拟、虚拟旅游和其他VR内容。客户可…...
【智能家居入门1之环境信息监测】(STM32、ONENET云平台、微信小程序、HTTP协议)
作为入门本篇只实现微信小程序接收下位机上传的数据,之后会持续发布如下项目:①可以实现微信小程序控制下位机动作,真正意义上的智能家居;②将网络通讯协议换成MQTT协议再实现上述功能,此时的服务器也不再是ONENET&…...
)
AIGC安全研究简述(附资料下载)
2023 AIGC技术实践及展望资料合集(29份).zip 2023 AIGC大型语言模型(LLM)实例代码合集.zip 2023大模型与AIGC峰会(公开)PPT汇总(25份).zip AIGC的安全研究是一个复杂且重要的领域,涉及多个关键…...
初识Spring MVC
什么是Spring MVC? 官方给的解释是 Spring Web MVC 是基于 Servlet API 构建的原始 Web 框架,从⼀开始就包含在 Spring 框架中。它的 正式名称“Spring Web MVC”来⾃其源模块的名称(Spring-webmvc),但它通常被称为"Spring MVC" 注:Severlet是…...
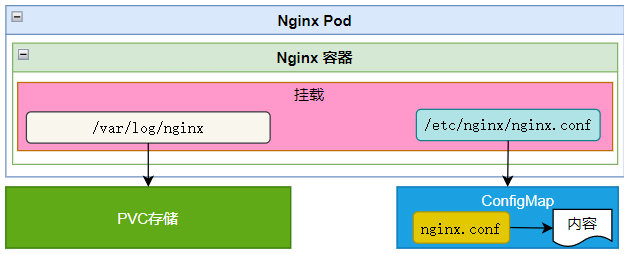
云原生之容器编排实践-ruoyi-cloud项目部署到K8S:Nginx1.25.3
背景 前面搭建好了 Kubernetes 集群与私有镜像仓库,终于要进入服务编排的实践环节了。本系列拿 ruoyi-cloud 项目进行练手,按照 MySQL , Nacos , Redis , Nginx , Gateway , Auth ,…...
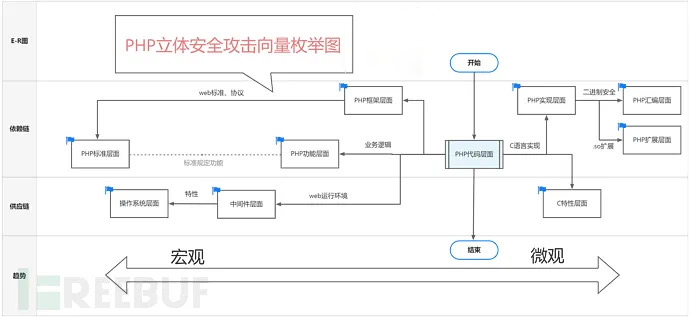
PHP立体安全攻击向量:保护应用程序的关键挑战
PHP立体安全攻击向量:保护应用程序的关键挑战 PHP作为一种广泛使用的服务器端脚本语言,拥有庞大的用户群体和丰富的生态系统。然而,随着互联网的发展,网络安全问题也变得愈发严重。本文将深入探讨PHP的立体安全攻击向量࿰…...
【功能大全】手机短信验证码一键注册登录流程
目录 发送验证码 注册登录 用户表设计 编辑申请腾讯云短信与密钥 找到云短信服务 开通腾讯云短信服务 编辑创建短信签名 编辑编辑创建短信正文模版编辑编辑 等待审核 测试短信编辑 SDK密钥创建 SpringBoot集成腾讯云短信 pom中导入腾讯云短…...

【Python】【Matplotlib】深入解析plt.grid()---原理、应用与注意事项
【Python】【Matplotlib】深入解析plt.grid()—原理、应用、源码与注意事项 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、PyTorch零基础入门教程Ǵ…...

数据库规范化设计案例解析
1.介绍 数据库规范化设计是数据库设计的一种重要方法,旨在减少数据库中的冗余数据,提高数据的一致性,确保数据依赖合理,从而提高数据库的结构清晰度和维护效率。规范化设计通过应用一系列的规范化规则(或称“范式”&a…...
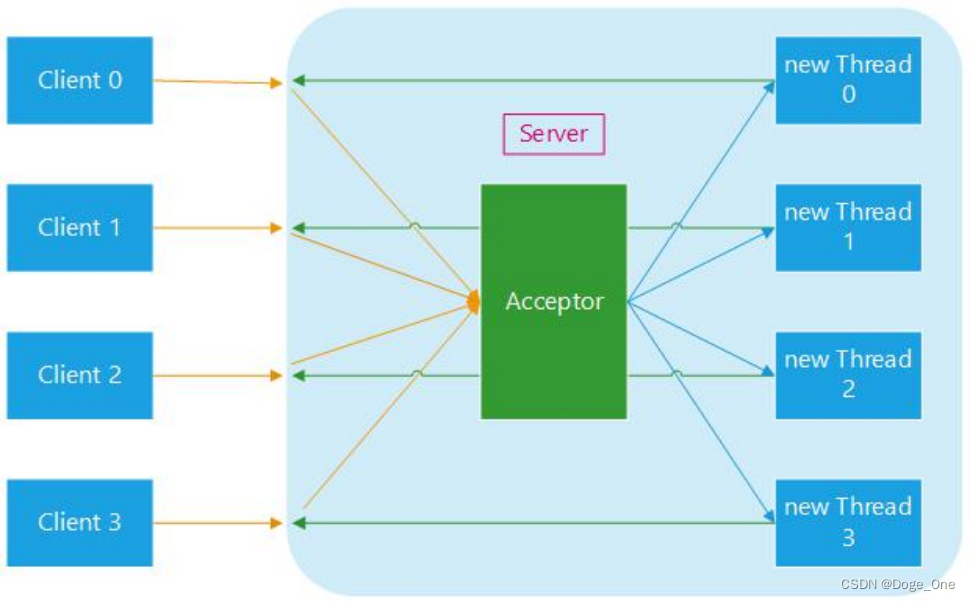
服务器段的连接端口和监听端口编程实现
new ServerSocket(int)是开启监听端口,并不是连接端口。真正的连接端口是随机开辟的空闲端口,当连接创建完成后,监听关口可以继续等待下一次连接请求,处于空闲等待状态。 编程实现方式 1 、主线程一直处于阻塞等待状态,…...

用“定时执行专家”武装你的电脑,做时间管理大师!
简介 你是否厌倦了重复繁琐的电脑操作?你是否希望能够解放双手,提高工作效率?“定时执行专家”是一款功能强大的定时任务执行软件,可以帮你轻松实现自动化办公,让你成为时间管理大师! 软件功能 支持25种任…...

css3实现3D立方体旋转特效源码
源码介绍 CSS3自动旋转正方体3D特效是一款基于css3 keyframes属性制作的图片相册自动旋转立方体特效 效果展示 下载地址 css3实现3D立方体旋转特效代码...

计算器系统基础知识-校验码
1.奇偶校验码 通过在编码中增加一位奇数校验位来使编码中1的个数为奇数(奇校验)或者为偶数(偶校验),从而使码距变为2。 常见的奇偶校验码有三种:水平奇偶校验码、垂直奇偶校验码和水平垂直校验码。 以下是奇偶校验码的示例: public …...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...
