代码随想录算法训练营第五十九天丨503. 下一个更大元素 II、42. 接雨水
503. 下一个更大元素 II
还是比较容易想的,扩展数组一倍即可。
class Solution:def nextGreaterElements(self, nums: List[int]) -> List[int]:extended_nums = nums * 2n = len(nums)mono = []res = [- 1] * nfor i, num in enumerate(extended_nums):while mono and extended_nums[mono[-1]] < num:if mono[-1] < n:res[mono[-1]] = nummono.pop()mono.append(i)return res看了代码随想录的题解可以用%运算减少空间复杂度。
class Solution:def nextGreaterElements(self, nums: List[int]) -> List[int]:n = len(nums)mono = []res = [- 1] * nfor i in range(2 * n):while mono and nums[mono[-1]] < nums[i % n]:res[mono[-1]] = nums[i % n]mono.pop()mono.append(i % n)return res42. 接雨水
手撕成功!
维护单调栈找右边第一个大的就是右边界,这时候把当前元素pop出来,如果栈不为空,说明左边也有比当前元素大的左边界,那么这俩边界之间就可以接雨水!!!
class Solution:def trap(self, height: List[int]) -> int:res = 0mono = []for right in range(len(height)):while mono and height[mono[-1]] < height[right]:cur = mono.pop()if mono:left = mono[-1]res += (right - left - 1) * (min(height[left], height[right]) - height[cur])mono.append(right)return res信心巨大增强!!!
记录一下双指针暴力解法:
class Solution:def trap(self, height: List[int]) -> int:n = len(height)if n == 0:return 0ans = 0for i in range(1, n - 1): # 对于每个位置max_left = max(height[:i]) # 找到左边的最大值max_right = max(height[i+1:]) # 找到右边的最大值# 计算当前位置能接的雨水量water = min(max_left, max_right) - height[i]if water > 0:ans += waterreturn ans动态规划解法:
class Solution:def trap(self, height: List[int]) -> int:n = len(height)left_max = [0] * nright_max = [0] * nans = 0# 从左向右计算左侧最大高度left_max[0] = height[0]for i in range(1, n):left_max[i] = max(left_max[i - 1], height[i])# 从右向左计算右侧最大高度right_max[n - 1] = height[n - 1]for i in range(n - 2, -1, -1):right_max[i] = max(right_max[i + 1], height[i])# 计算每个位置能接的雨水量,并累加for i in range(n):ans += min(left_max[i], right_max[i]) - height[i]return ans双指针究极优化:
class Solution:def trap(self, height: List[int]) -> int:left, right = 0, len(height) - 1 # 初始化左右指针left_max, right_max = height[left], height[right] # 初始化左右最大值ans = 0while left < right:# 更新左侧最大值和右侧最大值left_max = max(left_max, height[left])right_max = max(right_max, height[right])# 根据当前的最大值,计算能接的雨水,并移动指针if left_max < right_max:ans += left_max - height[left]left += 1else:ans += right_max - height[right]right -= 1return ans今日总结:
接雨水一刷AC,虽然花了1小时,成就感满满。
相关文章:

代码随想录算法训练营第五十九天丨503. 下一个更大元素 II、42. 接雨水
503. 下一个更大元素 II 还是比较容易想的,扩展数组一倍即可。 class Solution:def nextGreaterElements(self, nums: List[int]) -> List[int]:extended_nums nums * 2n len(nums)mono []res [- 1] * nfor i, num in enumerate(extended_nums):while mono…...
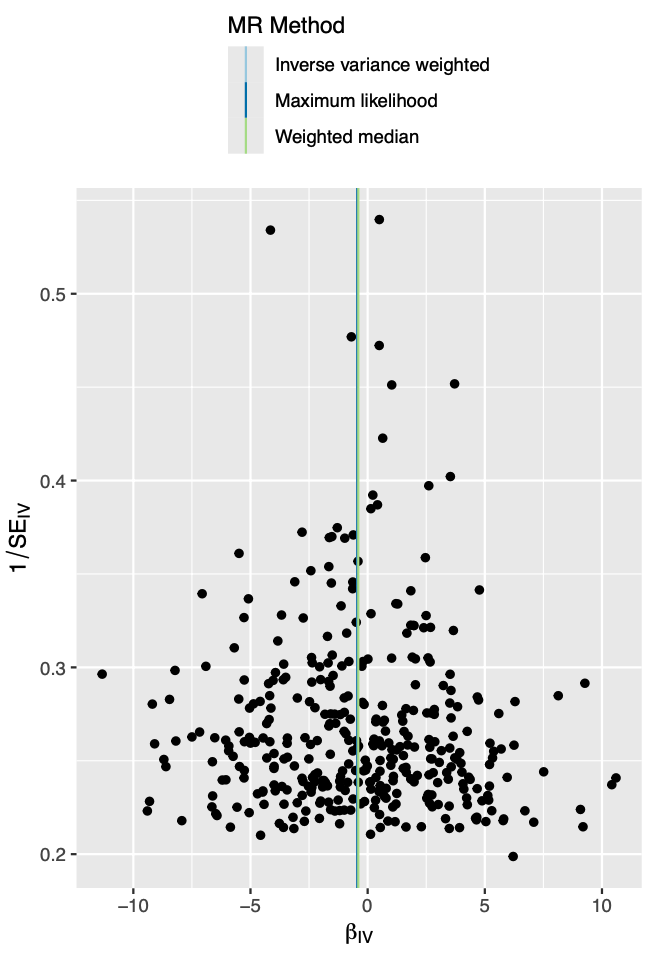
全代码分享|R语言孟德尔随机化怎么做?TwoSampleMR包MR一套标准流程
文章目录 1.前言1.1 成立条件1.2 三大要素1.3 统计原理 2.demo2.1 加载R包2.2 主要MR分析2.3 MR补充分析、多态性、验证 2.4 结果可视化 1.前言 孟德尔随机化(Mendelian randomization,MR)是一种利用基因变异作为工具变量来评估暴露与结果之间因果关系的统计方法。…...

【AI视野·今日NLP 自然语言处理论文速览 第八十四期】Thu, 7 Mar 2024
AI视野今日CS.NLP 自然语言处理论文速览 Thu, 7 Mar 2024 Totally 52 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers The Heuristic Core: Understanding Subnetwork Generalization in Pretrained Language Models Authors Adith…...

英伟达推出免训练,可生成连贯图片的文生图模型ConsiStory,生成角色一致性解决新方案
目前,多数文生图模型皆使用的是随机采样模式,使得每次生成的图像效果皆不同,在生成连贯的图像方面非常差。 例如,想通过AI生成一套图像连环画,即便使用同类的提示词也很难实现。虽然DALLE 3和Midjourney可以对图像实现…...

Jmeter 性能 —— 50TPS与秒杀分析!
1、50tps——5tps分析 50tps基本上已经满足了大部分中小型企业要求了 需求:期望我项目的接口,都要能满足50tps? 算 50tps:50 个事务每秒50 t/s 1分钟:50\*60s 3000 事务1小时 3000 \* 60 180000 事务 1小时要处理…...

【前端】如何计算首屏及白屏时间
文章目录 一、首屏时间二、白屏时间 一、首屏时间 白屏时间:页面渲染完所有内容的时间 简单点就是在<body> 标签后写js代码计算,但是不是很准确 <head><title>白屏时间</title> </head> <body></body> <s…...
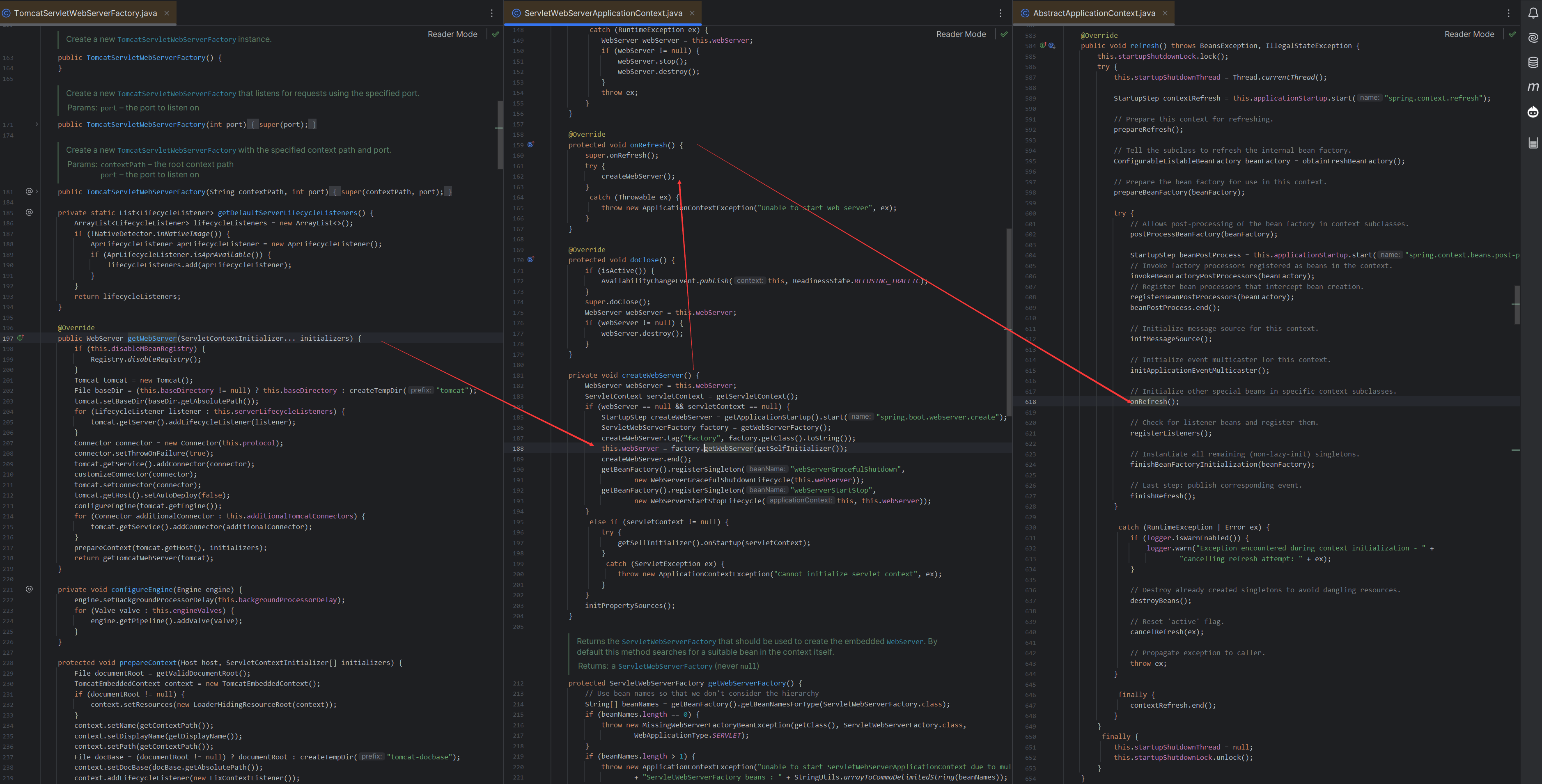
重学SpringBoot3-ServletWebServerFactoryAutoConfiguration类
更多SpringBoot3内容请关注我的专栏:《SpringBoot3》 期待您的点赞👍收藏⭐评论✍ 重学SpringBoot3-ServletWebServerFactoryAutoConfiguration类 工作原理关键组件以TomcatServletWebServerFactory为例ServletWebServerFactory会创建webServer的时机关键…...
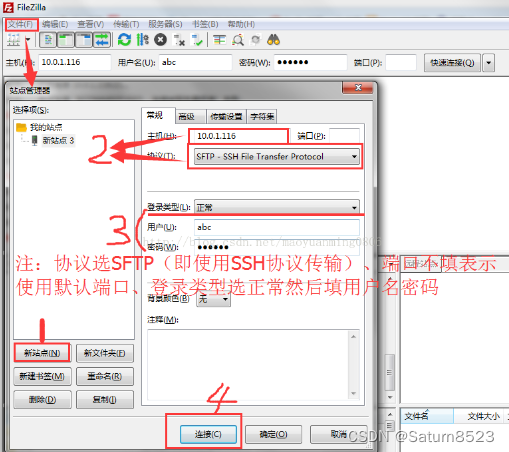
FileZillaClient连接被拒绝,无法连接
1.ECONNREFUSED - 连接被服务器拒绝 2、无法连接FZ时,判断没有ssh 更新源列表: sudo apt-get update 安装 openssh-server :sudo apt-get install openssh-server 查看是否启动ssh:sudo ps -e | grep ssh...

每日一面——成员初始化列表、移动构造和拷贝构造
写前声明:参考链接 C面经、面试宝典 等 ✊✊✊每日一面——成员初始化列表、移动构造和拷贝构造 一、类成员初始化方式?构造函数的执行顺序?为什么用成员初始化列表会快一些?二、final和override关键字三、拷贝初始化和直接初始化…...
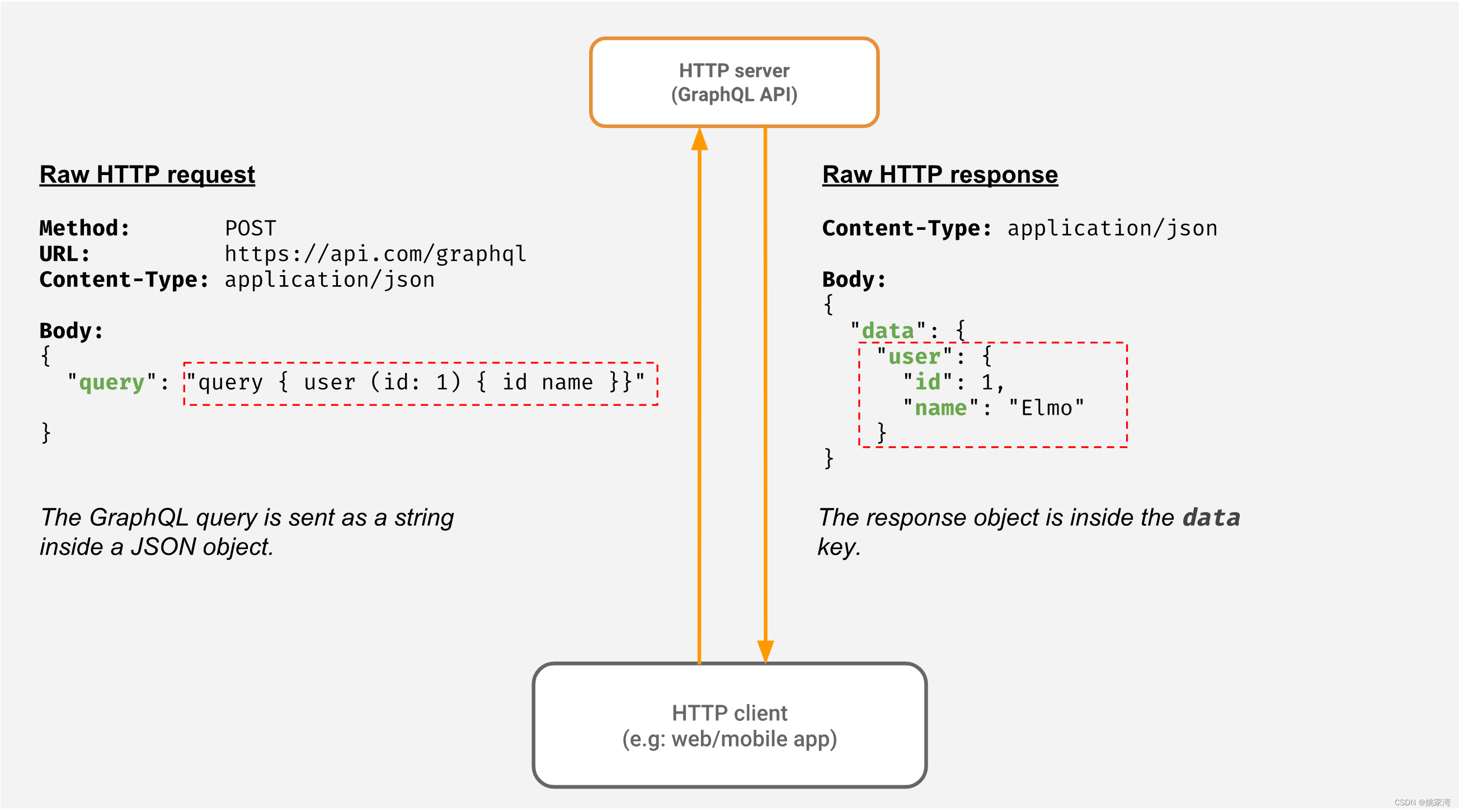
OPC UA 服务器的Web访问
基于Web 的应用非常普及,例如基于web 的SCADA ,物联网 Dashboard 等等,那么基于Web 的应用如何访问OPC UA 服务器呢?本博文讨论这方面的问题。 Web 的通信方式 Web 是我们通常讲的网站,它由浏览器,HTTP 服…...

docker 子网
当需要给容器分配指定 ip ,为避免ip 冲突,指定容器子网处理 创建 subnet 子网 docker network create --subnet 10.0.0.0/24 --gateway 10.0.0.1 subnet-testdocker network ls NETWORK ID NAME DRIVER SCOPE ... f582ecf297bc sub…...

QT使用RabbitMQ
文章目录 1.RabbitMQ 客户端下载地址:1.1RabbitMQ基本结构:2.搭建RabbitMQ server3.安装步骤4.运行4.1 报错问题解决5.使用5.1 配置Web管理界面6.常用命令总结7.Qt客户端编译7.1 这里重点强调一下,这个文件需要改成静态库7.2 下载地址:(qamqp自己下载,下载成功后,静态编译…...

什么是R语言?什么是R包?-R语言001
R语言是一种专为统计计算和图形而设计的编程语言和环境。它最初由罗斯伊哈卡和罗伯特亨特尔在1993年创建,灵感来源于S语言。R语言已经发展成为统计学、数据分析、科学研究以及许多其他领域中最受欢迎和广泛使用的工具之一。R语言的核心是一个开源的解释型语言&#…...

Java17 --- springCloud之LoadBalancer
目录 一、LoadBalancer实现负载均衡 1.1、创建两个相同的微服务 1.2、在客户端80引入loadBalancer的pom 1.3、80服务controller层: 一、LoadBalancer实现负载均衡 1.1、创建两个相同的微服务 1.2、在客户端80引入loadBalancer的pom <!--loadbalancer-->&…...
 使用 brew 安装nvm)
Mac(含M1) 使用 brew 安装nvm
目录 Mac 安装nvm 下载命令 配置环境变量 刷新 Mac(M1) 安装nvm 搜索 下载 为nvm创建文件夹 配置环境变量 刷新 Mac 安装nvm 下载命令 brew install nvm 配置环境变量 vi ~/.zshrc 内容如下: export NVM_DIR"$HOME/.nvm"[ -s "/usr/local…...
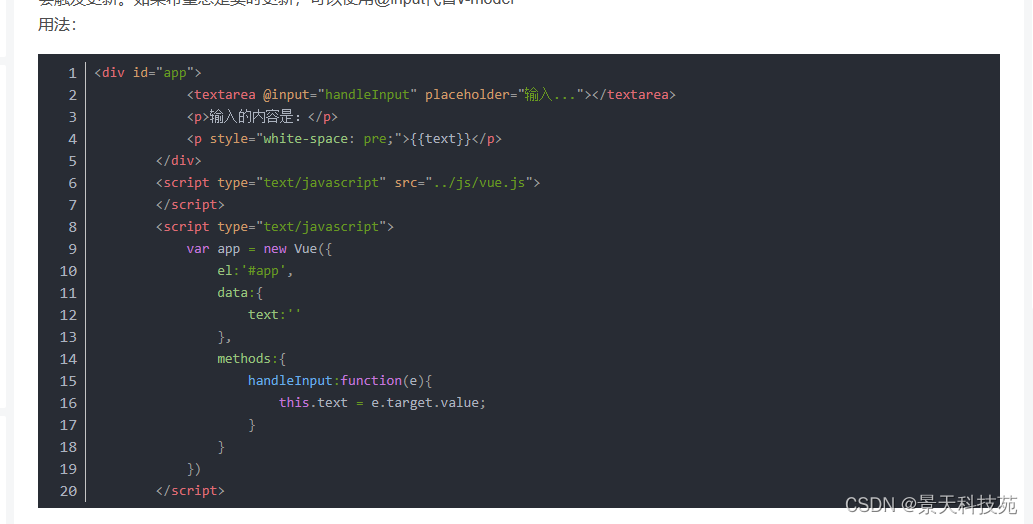
优秀的前端框架vue,原理剖析与实战技巧总结【干货满满】
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 所属的专栏:前端零基础教学,实战进阶 景天的主页:景天科技苑 文章目录 Vuevue.js库的基本使用vue.js的M-V-VM思…...

<2024最新>ChatGPT逆向教程
前言 在使用本篇文章用到的项目以及工具时,需要对其有一定的了解,无法访问以及无法使用的问题作者不承担任何责任,可以自行想办法解决遇到的问题。 文章若有不合适,有问题的地方,请私聊指出,谢谢~ 准备工具 一台至少 2 核 2G 内存的服务器,推荐是位于香港、新加坡或…...

C#编程技巧--2
1.使用泛型: 泛型允许你编写更加灵活和可重用的代码,同时提高类型安全性。 C# 中的泛型功能允许你编写更加灵活和可重用的代码,并且可以增加类型安全性。通过使用泛型,你可以编写适用于不同类型的代码,而无需为每种类型单独重写代…...

设计模式 代理模式
代理模式主要使用了 Java 的多态,主要是接口 干活的是被代理类,代理类主要是接活, 你让我干活,好,我交给幕后的类去干,你满意就成,那怎么知道被代理类能不能干呢? 同根就成ÿ…...

关于学习时间
这篇文章我来说一下我对于我最近学习时间的一些思考。 早上和下午是我最为活跃和高效的时间段。 我能够专注地工作,不容易分心。 然而,到了晚上,我的状态开始下降,这是很正常的情况。 由于早上和下午的专注学习,我的大…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
