全代码分享|R语言孟德尔随机化怎么做?TwoSampleMR包MR一套标准流程
文章目录
- 1.前言
- 1.1 成立条件
- 1.2 三大要素
- 1.3 统计原理
- 2.demo
- 2.1 加载R包
- 2.2 主要MR分析
- 2.3 MR补充分析、多态性、验证
- 2.4 结果可视化
1.前言
孟德尔随机化(Mendelian randomization,MR)是一种利用基因变异作为工具变量来评估暴露与结果之间因果关系的统计方法。
它基于这样的原理:基因变异是在出生前就随机分配给个体的,类似于在随机对照试验中随机分配治疗,因此可以帮助区分因果关系和简单相关性。孟德尔随机化通常用于观察性数据,以确定一个特定的生物标志物、行为或其他暴露是否真正地影响了健康结果,而不是仅仅与之相关。通过这种方法,研究者可以减少混杂因素的影响,避免了传统观察性研究中常见的一些偏差。
1.1 成立条件
孟德尔随机化方法的关键在于三个基本假设的成立:
- 相关性假设(Relevance assumption):所选的遗传变异与暴露因素必须有明确的关联。这意味着这些遗传变异能够作为影响暴露水平的可靠指标。
- 独立性假设(Independence assumption):遗传变异与任何影响结果的混杂因素必须独立。基于孟德尔遗传定律,遗传变异在受精时随机分配给后代,这个随机分配过程保证了其与后天环境因素的独立性。
- 排他性假设(Exclusion restriction assumption):遗传变异对结果的影响只能通过其对暴露的影响来体现,不应存在其他路径。这意味着遗传变异与结果之间的关联完全是通过暴露因素介导的。
孟德尔随机化的实施通常需要大量的基因组数据,包括与暴露因素和结果变量相关的遗传变异信息。通过统计分析这些数据,研究者可以估计出暴露与结果之间的因果关系大小。
这种方法在流行病学和遗传流行病学领域尤其有用,特别是在探索疾病的潜在风险因素时。不过,孟德尔随机化研究的解释需要谨慎,因为违反上述任一假设都可能导致估计的偏误。此外,该方法还受限于可用的遗传变异信息和样本大小。
1.2 三大要素
在孟德尔随机化研究中,主要涉及三个关键组成部分:暴露因素、结果,以及作为连接两者的桥梁的遗传变异。
暴露因素:这指的是可能对某个健康结果产生影响的任何因素,如生活方式、环境因素、生物标志物等。在孟德尔随机化中,研究人员试图评估这种暴露是否对结果具有因果效应。例如,暴露因素可以是饮酒量、体育锻炼、血压或血脂水平等。
结果:这是研究的终点,通常是健康相关的结果,如疾病发生、健康状况指标、生理测量值等。在孟德尔随机化研究中,结果是研究者试图了解其是否受到暴露因素的影响。例如,结果可以是心血管疾病、糖尿病、肥胖或寿命等。
遗传变异:在孟德尔随机化框架中,遗传变异是连接暴露因素和结果的关键。这些遗传变异(通常是单核苷酸多态性,SNPs)根据遗传原理,在人群中随机分布,与暴露因素具有相关性但又不受后天环境因素的影响。遗传变异作为工具变量,其作用是帮助研究者推断暴露因素与结果之间的因果关系,而不是仅仅描述它们之间的关联。这些遗传变异必须满足特定条件,即与暴露因素强相关、与混杂因素无关,且仅通过影响暴露因素来影响结果。
1.3 统计原理
孟德尔随机化分析中通常使用的是工具变量(IV)估计的数学框架。这个框架可以帮助我们理解如何通过遗传变异(作为工具变量)来估计一个暴露因素对结果的因果效应。下面是一个简化的版本,描述了这一过程中涉及的主要步骤和公式。
看起来你对LaTeX格式的数学公式表示很感兴趣!那么,按照你提供的官方格式,孟德尔随机化中的关键公式也可以这样优雅地展示:
-
第一阶段回归:
给定遗传变异 (Z) 对暴露因素 (X) 的影响可以表示为:
X = α + β Z X Z + ϵ X = \alpha + \beta_{ZX}Z + \epsilon X=α+βZXZ+ϵ
其中,(X) 代表暴露因素,(Z) 是遗传变异(工具变量),(\alpha) 是截距,(\beta_{ZX}) 表示遗传变异对暴露因素的影响程度,(\epsilon) 是误差项。 -
第二阶段回归:
调整后的暴露因素 (X) 对结果 (Y) 的影响可以通过下面的方程来估计:
Y = γ + β X Y X ^ + ν Y = \gamma + \beta_{XY}\hat{X} + \nu Y=γ+βXYX^+ν
这里,(Y) 表示结果变量,(\hat{X}) 是从第一阶段回归中得到的基于遗传变异的暴露因素预测值,(\gamma) 是截距,(\beta_{XY}) 是调整后的暴露因素对结果影响的因果效应系数,(\nu) 是误差项。 -
工具变量估计的因果效应:
暴露因素 (X) 对结果 (Y) 的因果效应可以通过下面的比率来估计:
β ^ X Y = Cov ( Z , Y ) Cov ( Z , X ) \hat{\beta}_{XY} = \frac{\text{Cov}(Z, Y)}{\text{Cov}(Z, X)} β^XY=Cov(Z,X)Cov(Z,Y)
其中,(\hat{\beta}_{XY}) 是通过遗传工具变异估计的暴露因素对结果影响的因果效应系数,(\text{Cov}(Z, Y)) 和 (\text{Cov}(Z, X)) 分别表示遗传变异与结果变量以及遗传变异与暴露因素之间的协方差。
另外可以看一下前一篇的文献分享:
两步法的双样本孟德尔随机化怎么做?2暴露因素+4风险因素+3结果
2.demo
这里复现的是教育年限对EC的影响
2.1 加载R包
library(devtools)
library(tidyr)
# devtools::install_github("MRCIEU/MRInstruments")
library(MRInstruments)
library(MendelianRandomization)
library(TwoSampleMR)
#install.packages("simex")
library(simex)
#install_github("rondolab/MR-PRESSO")
library(MRPRESSO)
2.2 主要MR分析
mydata <- read.table("01mydata_edu_cancer.txt", header=T, sep="\t", check.names = F, stringsAsFactors = F)
heterogeneity <- mr_heterogeneity(mydata)
heterogeneity
# id.exposure id.outcome outcome exposure method Q Q_df Q_pval
# 1 ieu-a-1001 lAx3ZW outcome || id:ieu-a-1001 MR Egger 347.7875 362 0.6951200
# 2 ieu-a-1001 lAx3ZW outcome || id:ieu-a-1001 Inverse variance weighted 347.8263 363 0.7075905### 二选一
# 2.1 如果I2<25%或Q_P>0.05,使用固定效应的逆方差加权法(IVW)
mr_results <- mr(mydata, method_list=c('mr_ivw_fe'))
mr_results
generate_odds_ratios(mr_results)
# 2.2 如果I2>25%且Q_P<0.05,使用随机效应的逆方差加权法(IVW)
mr_results <- mr(mydata, method_list=c('mr_ivw_mre'))
mr_results
generate_odds_ratios(mr_results)
2.3 MR补充分析、多态性、验证
选择加权还是不加权取决于数据特性和分析目的,当所有基因-暴露估计的可变性(标准误)大致相同时,不加权的方法可能更为适用,反之则使用加权。
教大家一个更简单的方法:加权和不加权都做,选结果好的(P值更显著的),如果都显著则选择加权的,因为它还照顾到每个点的不确定性,更为全面
mr_results1 <- mr(mydata, method_list=c('mr_two_sample_ml', 'mr_egger_regression',"mr_simple_median", "mr_weighted_median", "mr_penalised_weighted_median","mr_simple_mode", "mr_weighted_mode"))
mr_results1# 4.1 MR-Egger截距测试
mr_pleiotropy_test(mydata)
mr_egger(mr_input(bx = mydata$beta.exposure, bxse = mydata$se.exposure, by = mydata$beta.outcome, byse = mydata$se.outcome)) # 4.2 MR多态性残差和异常值(MR-PRESSO)测试
# 运行MR-PRESSO全局方法
mr_presso(BetaOutcome = "beta.outcome", BetaExposure = "beta.exposure", SdOutcome = "se.outcome", SdExposure = "se.exposure", OUTLIERtest = TRUE, DISTORTIONtest = TRUE, data = mydata, NbDistribution = 1000, SignifThreshold = 0.05, seed = 123456) # 5.1 IVW radial: mr_ivw_radial
mr(mydata, method_list=c("mr_ivw_radial"))
# 5.2 Egger-SIMEXS
mr_egger(mr_input(bx = mydata$beta.exposure, bxse = mydata$se.exposure, by = mydata$beta.outcome, byse = mydata$se.outcome))
BetaXG <- mydata$beta.exposure
BetaYG <- mydata$beta.outcome
seBetaXG <- mydata$se.exposure
seBetaYG <- mydata$se.outcome
BYG <- BetaYG * sign(BetaXG) # 预处理步骤,确保所有基因-暴露估计都是正的
BXG <- abs(BetaXG) # MR-Egger回归(未加权)
Fit1 <- lm(BYG ~ BXG, x=TRUE, y=TRUE)
mod.sim1 <- simex(Fit1, B=1000, measurement.error = seBetaXG, SIMEXvariable="BXG", fitting.method ="quad", asymptotic="FALSE")
summary(mod.sim1)
# MR-Egger回归(加权)
Fit2 <- lm(BYG ~ BXG, weights=1/seBetaYG^2, x=TRUE, y=TRUE)
mod.sim2 <- simex(Fit2, B=1000, measurement.error = seBetaXG, SIMEXvariable="BXG", fitting.method ="quad", asymptotic="FALSE")
summary(mod.sim2)# IVW不加权
Fit3 <- lm(BYG ~ -1 + BXG, x=TRUE, y=TRUE)
mod.sim3 <- simex(Fit3, B=1000, measurement.error = seBetaXG, SIMEXvariable="BXG", fitting.method="quad", asymptotic="FALSE")
summary(mod.sim3)
# IVW加权
Fit4 <- lm(BYG ~ -1 + BXG, weights=1/seBetaYG^2, x=TRUE, y=TRUE)
mod.sim4 <- simex(Fit4, B=1000, measurement.error = seBetaXG, SIMEXvariable="BXG", fitting.method="quad", asymptotic="FALSE")
summary(mod.sim4)
2.4 结果可视化
library(ggplot2)
# 散点图
plot1 <- mr_scatter_plot(mr_results1, mydata)
plot1# 单个SNP森林图
res_single <- mr_singlesnp(mydata,parameters = default_parameters(),single_method = "mr_wald_ratio",all_method = c("mr_ivw", 'mr_two_sample_ml', "mr_weighted_median")
)
significant_snps <- res_single[res_single$p < 0.05, ] # 只保留P<0.05
plot2 <- mr_forest_plot(significant_snps)
plot2# 留一法敏感性测试
single <- mr_leaveoneout(mydata)
top_30 <- single[order(single$p), ][1:30, ] # 只保留P最小的前30个
plot3 <- mr_leaveoneout_plot(top_30)
plot3# 漏斗图
plot4 <- mr_funnel_plot(res_single)
plot4
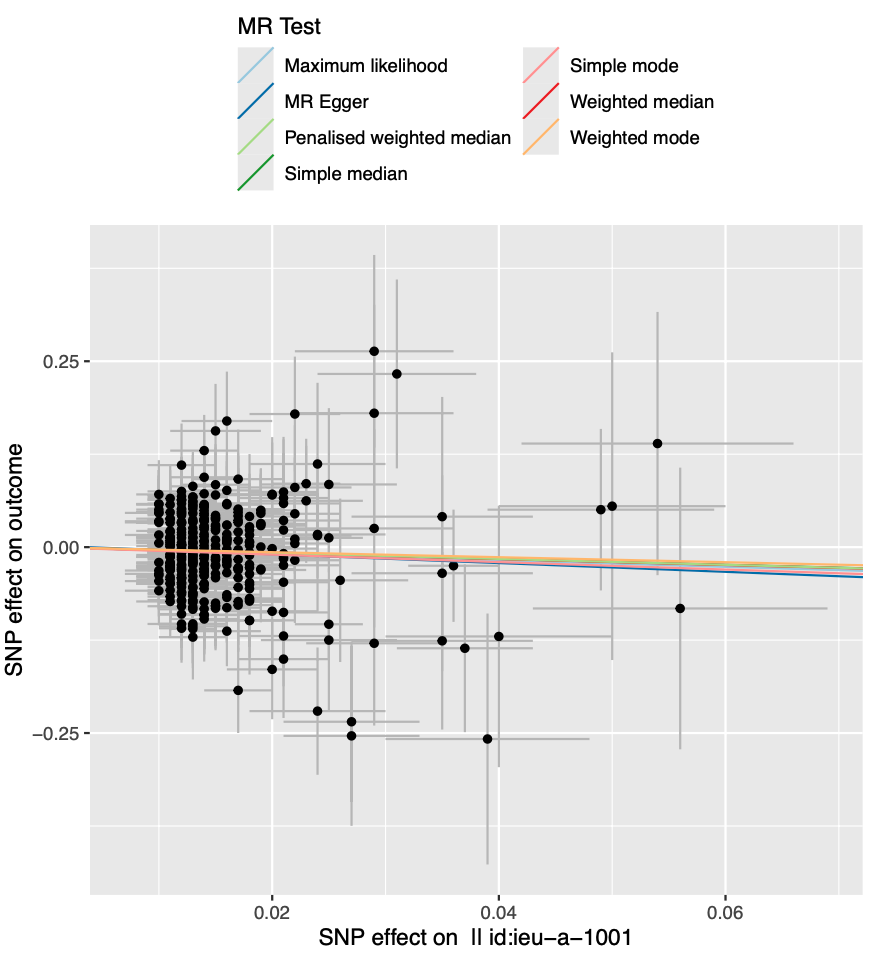 这个图是一个孟德尔随机化(MR)分析的散点图,通常用来评估遗传变异对某个健康结果的影响,并且试图解释这种影响是否有可能是因果的。在这个图中,每个点代表一个单独的遗传变异(通常是单核苷酸多态性,SNP)。横轴显示了每个SNP对暴露因素(例如某种生理指标或行为)的影响大小,而纵轴显示了每个SNP对结果(例如某种疾病或健康状况)的影响大小。每个点的位置表示了暴露和结果的关联,而点的大小可能表示了这种关联的统计权重,或者样本中该变异的频率。
这个图是一个孟德尔随机化(MR)分析的散点图,通常用来评估遗传变异对某个健康结果的影响,并且试图解释这种影响是否有可能是因果的。在这个图中,每个点代表一个单独的遗传变异(通常是单核苷酸多态性,SNP)。横轴显示了每个SNP对暴露因素(例如某种生理指标或行为)的影响大小,而纵轴显示了每个SNP对结果(例如某种疾病或健康状况)的影响大小。每个点的位置表示了暴露和结果的关联,而点的大小可能表示了这种关联的统计权重,或者样本中该变异的频率。
具体来说,图中展示了不同MR测试方法的结果线,这些线通常用于评估MR分析的整体趋势,这些方法可能包括:
| Type | Note |
|---|---|
| MR Egger | 这是一种检测和校正遗传仪表变量偏差的方法,用来评估遗传工具的有效性和存在潜在的选择性混杂。 |
| 加权中位数(Weighted median) | 这种方法允许部分遗传工具变量是无效的,但假定至少一半的工具变量信息是有效的。 |
| 惩罚加权中位数(Penalised weighted median) | 类似于加权中位数,但是通过对变异点施加惩罚来减少个别点的影响力,通常是为了控制极端值。 |
| 简单模式(Simple mode)和加权模式(Weighted mode) | 评估最常见的效应大小或者考虑了权重的效应大小。 |
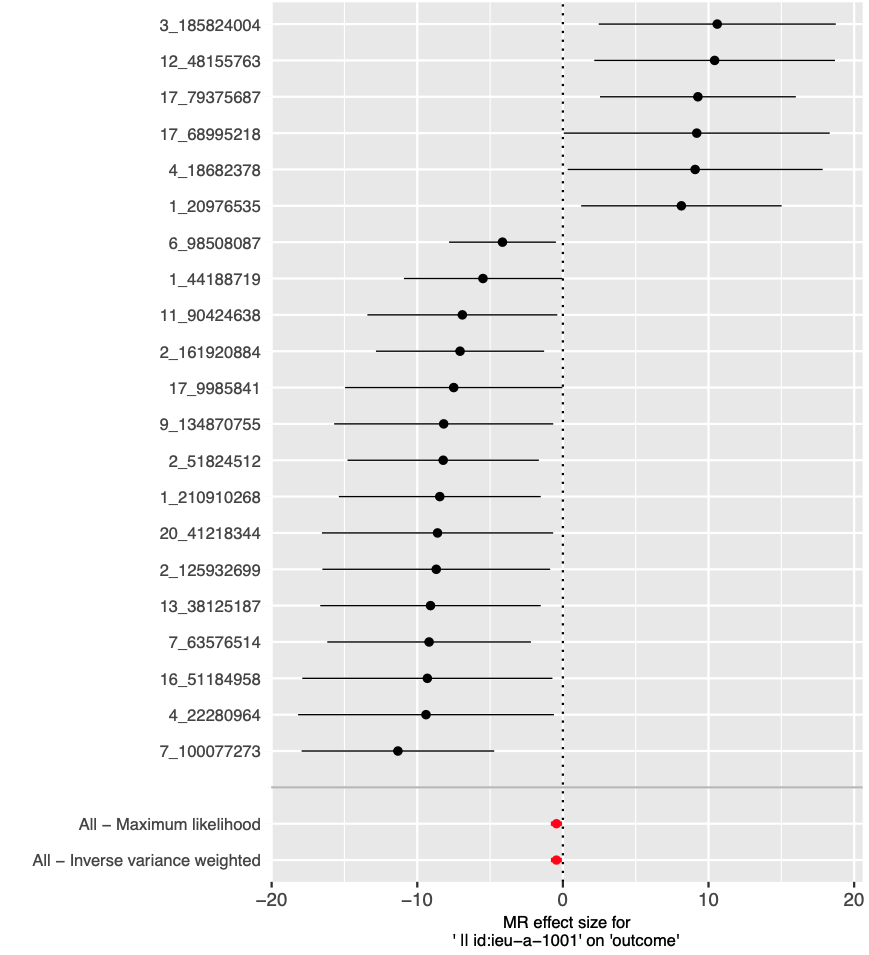
这张图是一个孟德尔随机化(MR)分析的森林图,展示了一系列遗传变异(单核苷酸多态性,SNPs)对某个结果的影响大小。在森林图中,每个水平线段代表一个SNP的估计效应及其95%置信区间,点代表估计效应的中心值。这种图形用于显示多个研究或分析的结果,并通常包括一个汇总的估计效应。
具体来说,左侧的数字可能是SNPs的编号或者是它们位于基因组上的位置(例如染色体上的特定位置)。中间的黑点代表每个SNP对结果的估计效应大小,而横向的线表示估计效应的置信区间;如果线越短,表示估计的不确定性越小。
在图的底部,有两个综合的点估计和置信区间:
| Type | Note |
|---|---|
| All – Maximum likelihood | 表示使用最大似然法对所有SNPs的效应大小进行综合估计。 |
| All – Inverse variance weighted | 表示使用逆方差加权法汇总所有SNPs的效应,这是最常用的汇总方法,给予不确定性较小的估计更大的权重。 |
红色的点估计和置信区间通常指示存在一个或多个离群值或强烈的偏离,这可能意味着那些特定的遗传变异与结果之间的关联可能受到了某些混杂因素或特定偏倚的影响。
该森林图提供了一个直观的方式来评估各个遗传变异对结果的可能影响,并且可以帮助研究人员判断是否有足够的证据支持遗传变异和结果之间的因果关系。在这种分析中,如果汇总估计的置信区间不包括零(垂直虚线),则通常被认为是有统计学意义的。在这张图中,大多数点的置信区间都跨过了零点线,暗示单个SNP的效应可能不具有统计学意义;但汇总效应点估计偏离零,表明可能存在暴露和结果之间的总体关联。然而,需要进一步的分析来确认这些发现。 这个图是一个“leave-one-out”敏感性分析的森林图,它用于孟德尔随机化(MR)研究中。在这种分析中,每次从分析中排除一个遗传变异(SNP),然后重新计算暴露因素对结果的影响,这样可以评估每个SNP对整体估计结果的影响程度。
这个图是一个“leave-one-out”敏感性分析的森林图,它用于孟德尔随机化(MR)研究中。在这种分析中,每次从分析中排除一个遗传变异(SNP),然后重新计算暴露因素对结果的影响,这样可以评估每个SNP对整体估计结果的影响程度。
在图中,每条水平线代表除了一个特定SNP之外的所有SNPs对结果影响的估计。横轴显示了估计效应的大小,点代表估计效应的中心值,线表示95%置信区间。
左侧的数字很可能是SNPs的标识符,可能是它们在基因组上的位置编号。
这种分析方法可以帮助研究人员识别任何可能异常影响整体分析结果的单个遗传变异。如果去除某个SNP后估计效应发生了显著变化,那么这个SNP可能是一个强烈的异常值或具有强烈的影响力。如果移除任何单一SNP后结果保持稳定,这表明MR分析的结果是稳健的,不会因单个SNP的异常而受到过度影响。
在图的底部,“All”项通常表示所有SNPs包含在内的总体效应大小估计。如果这个总体估计的置信区间不包括零点,这通常表明有一个统计上显著的效应。这张图显示的大多数点的置信区间都不包括零点,表明即使单独去除任何一个SNP,MR分析的结果也表明暴露可能对结果有显著影响。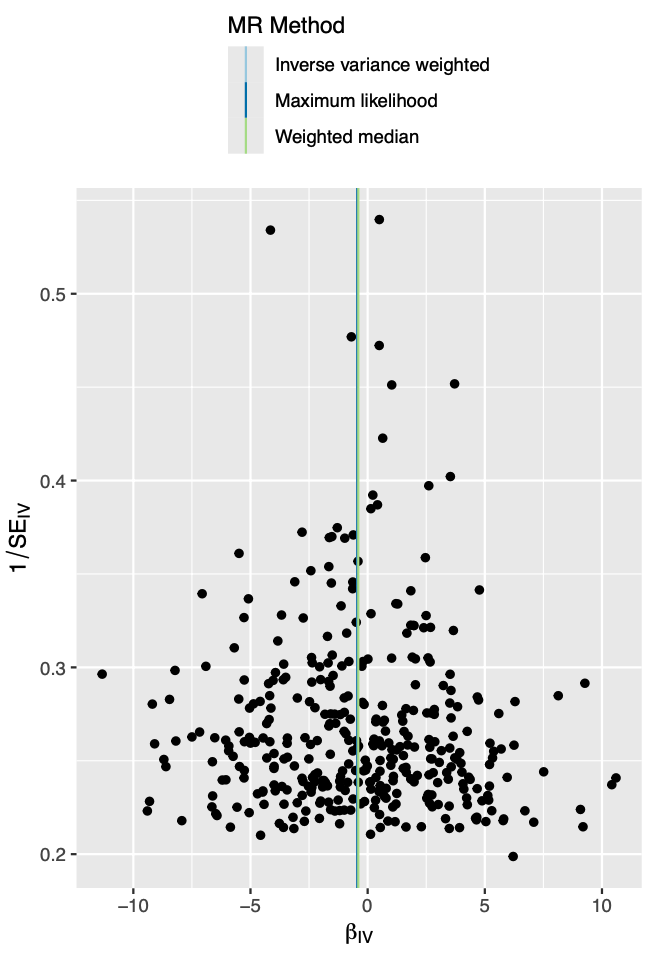
你提供的图是孟德尔随机化(MR)分析中常用的散点图,它用于展示遗传工具的效力(即遗传变异对暴露因素的影响大小)与它们对结果估计的因果效应大小之间的关系。
图中的横轴表示遗传变异对暴露因素的影响估计值,也就是效应大小。纵轴代表标准误差的倒数,用来表示每个估计的精确度;纵轴上方位置较高的点表明标准误差较小,估计的精确度更高。
在这种图中,我们通常会寻找是否存在漏斗形状,这样的形状意味着标准误差较大的估计(通常是效应大小较小的遗传变异)会更分散,而标准误差较小的估计则更集中。这有助于评估各个遗传变异作为工具变量时的稳健性和可信度。
图中还标注了不同的MR方法,例如逆方差加权(Inverse variance weighted)、最大似然(Maximum likelihood)和加权中位数(Weighted median)等,这些都是合成所有遗传变异影响的不同统计方法。
总体来说,这张图是在利用遗传信息探究特定暴露因素(如生活习惯、环境因素等)与健康结果(如某种疾病的风险)之间是否存在因果关系的工具。通过这种方法,研究人员可以在一定程度上避免传统观察性研究中常见的混淆因素,更可靠地揭示潜在的因果效应。
上述图注为GPT生成,实属无奈,纯代码分享但字数不够被定义为低质量文章,大家见谅
最后,示例数据仅供参考,笔者发现这个分析结果并不如意,权作教程示例数据使用,无实际意义!
有需要的小伙伴可以直接替换数据学起来吧~
多线程核糖体后台回复MR1领取示例文件与代码
相关文章:

全代码分享|R语言孟德尔随机化怎么做?TwoSampleMR包MR一套标准流程
文章目录 1.前言1.1 成立条件1.2 三大要素1.3 统计原理 2.demo2.1 加载R包2.2 主要MR分析2.3 MR补充分析、多态性、验证 2.4 结果可视化 1.前言 孟德尔随机化(Mendelian randomization,MR)是一种利用基因变异作为工具变量来评估暴露与结果之间因果关系的统计方法。…...

【AI视野·今日NLP 自然语言处理论文速览 第八十四期】Thu, 7 Mar 2024
AI视野今日CS.NLP 自然语言处理论文速览 Thu, 7 Mar 2024 Totally 52 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers The Heuristic Core: Understanding Subnetwork Generalization in Pretrained Language Models Authors Adith…...

英伟达推出免训练,可生成连贯图片的文生图模型ConsiStory,生成角色一致性解决新方案
目前,多数文生图模型皆使用的是随机采样模式,使得每次生成的图像效果皆不同,在生成连贯的图像方面非常差。 例如,想通过AI生成一套图像连环画,即便使用同类的提示词也很难实现。虽然DALLE 3和Midjourney可以对图像实现…...

Jmeter 性能 —— 50TPS与秒杀分析!
1、50tps——5tps分析 50tps基本上已经满足了大部分中小型企业要求了 需求:期望我项目的接口,都要能满足50tps? 算 50tps:50 个事务每秒50 t/s 1分钟:50\*60s 3000 事务1小时 3000 \* 60 180000 事务 1小时要处理…...

【前端】如何计算首屏及白屏时间
文章目录 一、首屏时间二、白屏时间 一、首屏时间 白屏时间:页面渲染完所有内容的时间 简单点就是在<body> 标签后写js代码计算,但是不是很准确 <head><title>白屏时间</title> </head> <body></body> <s…...
重学SpringBoot3-ServletWebServerFactoryAutoConfiguration类
更多SpringBoot3内容请关注我的专栏:《SpringBoot3》 期待您的点赞👍收藏⭐评论✍ 重学SpringBoot3-ServletWebServerFactoryAutoConfiguration类 工作原理关键组件以TomcatServletWebServerFactory为例ServletWebServerFactory会创建webServer的时机关键…...
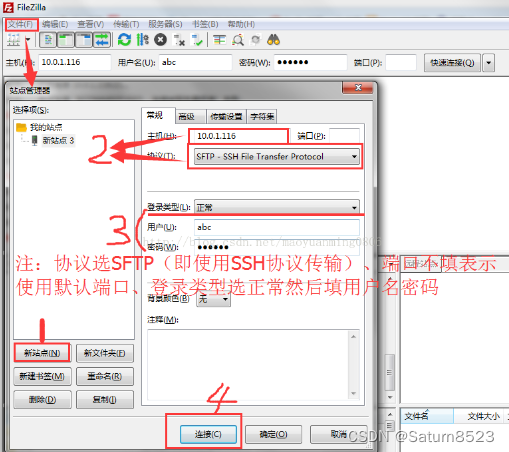
FileZillaClient连接被拒绝,无法连接
1.ECONNREFUSED - 连接被服务器拒绝 2、无法连接FZ时,判断没有ssh 更新源列表: sudo apt-get update 安装 openssh-server :sudo apt-get install openssh-server 查看是否启动ssh:sudo ps -e | grep ssh...

每日一面——成员初始化列表、移动构造和拷贝构造
写前声明:参考链接 C面经、面试宝典 等 ✊✊✊每日一面——成员初始化列表、移动构造和拷贝构造 一、类成员初始化方式?构造函数的执行顺序?为什么用成员初始化列表会快一些?二、final和override关键字三、拷贝初始化和直接初始化…...
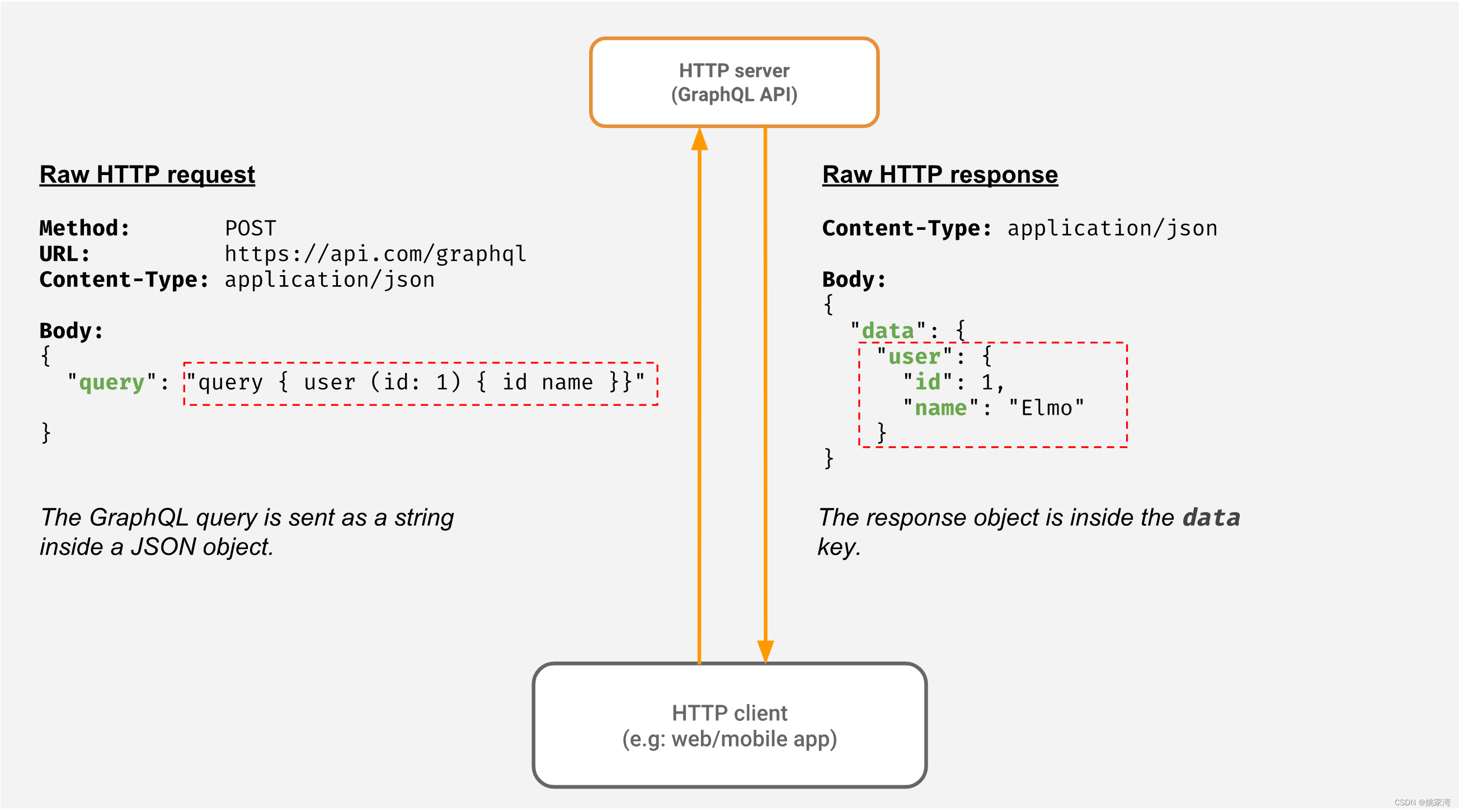
OPC UA 服务器的Web访问
基于Web 的应用非常普及,例如基于web 的SCADA ,物联网 Dashboard 等等,那么基于Web 的应用如何访问OPC UA 服务器呢?本博文讨论这方面的问题。 Web 的通信方式 Web 是我们通常讲的网站,它由浏览器,HTTP 服…...

docker 子网
当需要给容器分配指定 ip ,为避免ip 冲突,指定容器子网处理 创建 subnet 子网 docker network create --subnet 10.0.0.0/24 --gateway 10.0.0.1 subnet-testdocker network ls NETWORK ID NAME DRIVER SCOPE ... f582ecf297bc sub…...

QT使用RabbitMQ
文章目录 1.RabbitMQ 客户端下载地址:1.1RabbitMQ基本结构:2.搭建RabbitMQ server3.安装步骤4.运行4.1 报错问题解决5.使用5.1 配置Web管理界面6.常用命令总结7.Qt客户端编译7.1 这里重点强调一下,这个文件需要改成静态库7.2 下载地址:(qamqp自己下载,下载成功后,静态编译…...

什么是R语言?什么是R包?-R语言001
R语言是一种专为统计计算和图形而设计的编程语言和环境。它最初由罗斯伊哈卡和罗伯特亨特尔在1993年创建,灵感来源于S语言。R语言已经发展成为统计学、数据分析、科学研究以及许多其他领域中最受欢迎和广泛使用的工具之一。R语言的核心是一个开源的解释型语言&#…...

Java17 --- springCloud之LoadBalancer
目录 一、LoadBalancer实现负载均衡 1.1、创建两个相同的微服务 1.2、在客户端80引入loadBalancer的pom 1.3、80服务controller层: 一、LoadBalancer实现负载均衡 1.1、创建两个相同的微服务 1.2、在客户端80引入loadBalancer的pom <!--loadbalancer-->&…...
 使用 brew 安装nvm)
Mac(含M1) 使用 brew 安装nvm
目录 Mac 安装nvm 下载命令 配置环境变量 刷新 Mac(M1) 安装nvm 搜索 下载 为nvm创建文件夹 配置环境变量 刷新 Mac 安装nvm 下载命令 brew install nvm 配置环境变量 vi ~/.zshrc 内容如下: export NVM_DIR"$HOME/.nvm"[ -s "/usr/local…...
优秀的前端框架vue,原理剖析与实战技巧总结【干货满满】
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 所属的专栏:前端零基础教学,实战进阶 景天的主页:景天科技苑 文章目录 Vuevue.js库的基本使用vue.js的M-V-VM思…...

<2024最新>ChatGPT逆向教程
前言 在使用本篇文章用到的项目以及工具时,需要对其有一定的了解,无法访问以及无法使用的问题作者不承担任何责任,可以自行想办法解决遇到的问题。 文章若有不合适,有问题的地方,请私聊指出,谢谢~ 准备工具 一台至少 2 核 2G 内存的服务器,推荐是位于香港、新加坡或…...

C#编程技巧--2
1.使用泛型: 泛型允许你编写更加灵活和可重用的代码,同时提高类型安全性。 C# 中的泛型功能允许你编写更加灵活和可重用的代码,并且可以增加类型安全性。通过使用泛型,你可以编写适用于不同类型的代码,而无需为每种类型单独重写代…...

设计模式 代理模式
代理模式主要使用了 Java 的多态,主要是接口 干活的是被代理类,代理类主要是接活, 你让我干活,好,我交给幕后的类去干,你满意就成,那怎么知道被代理类能不能干呢? 同根就成ÿ…...

关于学习时间
这篇文章我来说一下我对于我最近学习时间的一些思考。 早上和下午是我最为活跃和高效的时间段。 我能够专注地工作,不容易分心。 然而,到了晚上,我的状态开始下降,这是很正常的情况。 由于早上和下午的专注学习,我的大…...
Github:Your browser did something unexpected. Please try again.
问题概述 Github:Your browser did something unexpected. Please try again. If the error continues, try disabling all browser extensions. 问题原因: 提示是插件出了问题,关闭了所有插件也无法解决,搜索了一下说是VPN的问题…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
