【数据结构学习笔记】选择排序
【数据结构学习笔记】选择排序
参考电子书:排序算法精讲
算法原理
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕
const nums = [1, 4, 6, 2, 0];let minIndex;
for (let i = 0; i < nums.length; i++) {minIndex = i;for (let j = i + 1; j < nums.length; j++) {if (nums[j] < nums[minIndex]) {minIndex = j;}}const temp = nums[i];nums[i] = nums[minIndex];nums[minIndex] = temp;
}
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
优化方式
- 当 i = nums.length - 1 时,j = nums.length 直接跳出循环,因此可以跳过
const nums = [1, 4, 6, 2, 0];let minIndex;
for (let i = 0; i < nums.length - 1; i++) {minIndex = i;for (let j = i + 1; j < nums.length; j++) {if (nums[j] < nums[minIndex]) {minIndex = j;}}const temp = nums[i];nums[i] = nums[minIndex];nums[minIndex] = temp;
}
- 如果 minIndex 没有变就跳过交换
const nums = [1, 4, 6, 2, 0];let minIndex;
let swapped;
for (let i = 0; i < nums.length; i++) {minIndex = i;swapped = false;for (let j = i + 1; j < nums.length - i; j++) {if (nums[j] < nums[minIndex]) {minIndex = j;swapped = true;}}if (!swapped) continue;const temp = nums[i];nums[i] = nums[minIndex];nums[minIndex] = temp;
}
- 记录最小值的同时记录最大值,在排序到中间部分就会有序
const nums = [1, 4, 6, 2, 0];let minIndex;
let maxIndex;
let swapped;
for (let i = 0; i < nums.length; i++) {minIndex = i;maxIndex = i;swapped = false;for (let j = i + 1; j < nums.length - i; j++) {if (nums[j] < nums[minIndex]) {minIndex = j;swapped = true;}if (nums[j] > nums[maxIndex]) {maxIndex = j;swapped = true;}}if (!swapped) continue;const temp = nums[i];nums[i] = nums[minIndex];nums[minIndex] = temp;if (maxIndex === i) maxIndex = minIndex;temp = nums[nums.length - 1 - i];nums[nums.length - 1 - i] = nums[maxIndex];nums[maxIndex] = temp;
}
相关例题
LC 215.数组中的第 k 个最大元素
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
/*** @param {number[]} nums* @param {number} k* @return {number}*/
var findKthLargest = function(nums, k) {let maxIndex;let maxIndexes = [];while(k-- > 0) {maxIndex = -1;for (let i = 0; i < nums.length; i++) {if (maxIndexes.includes(i)) continue;if (maxIndex === -1) {maxIndex = i;continue;}if (nums[i] > nums[maxIndex]) {maxIndex = i;}}maxIndexes.push(maxIndex);}return nums[maxIndexes[maxIndexes.length - 1]];
};
受限于 Leetcode 更新了测试用例,此题用选择排序会出现超时,但是算法思想不变即可
相关文章:

【数据结构学习笔记】选择排序
【数据结构学习笔记】选择排序 参考电子书:排序算法精讲 算法原理 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元…...

小资金适合做伦敦金的投资吗?
在回答这个问题之前,我们首先需要了解伦敦金是什么。伦敦金,也称为伦敦金市场交易的黄金,是一种国际性的金融交易产品,其价格受全球政治、经济、货币政策、供求关系等多种因素影响,波动性较大。因此,投资伦…...
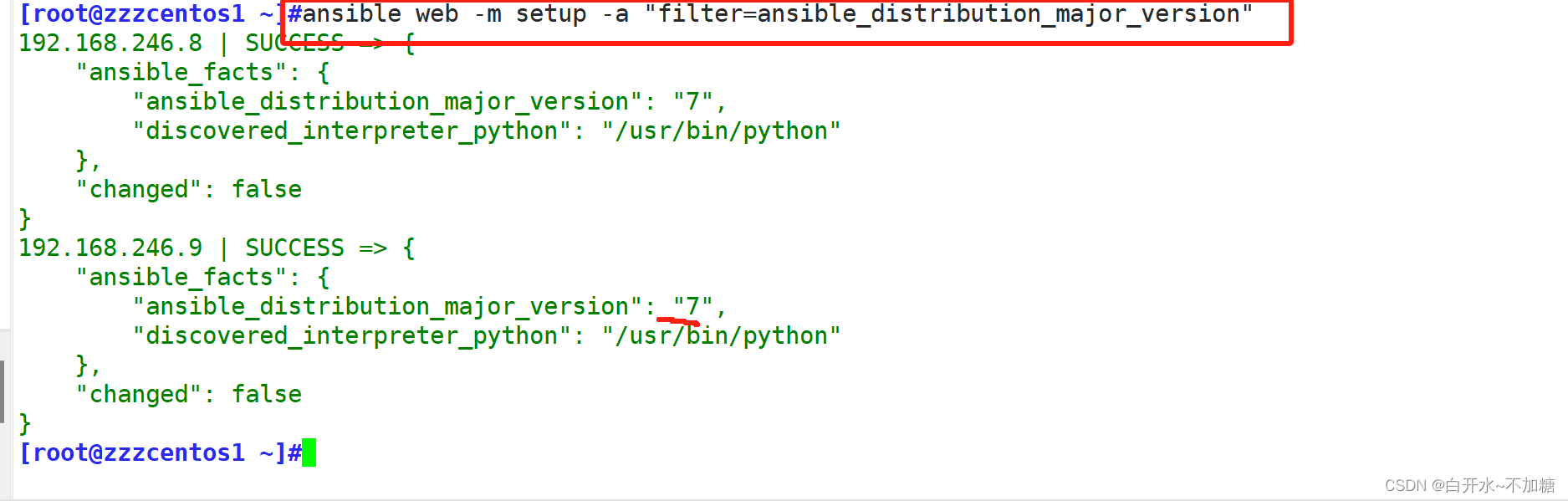
自动化运维工具 ---------------Ansible
一、Ansible 发展史及功能 作者:Michael DeHaan( Cobbler pxe kikstar 与 Func 作者)ansible 的名称来自科幻小说《安德的游戏》中跨越时空的即时通信工具,使用它可以在相距数光年的距离,远程实时控制前线的舰队战斗2…...

富格林:有效做单安全盈利方法
富格林悉知,在伦敦金的投资中,是否安全盈利很大一部分因素取决于是否有效做单,投资者在进入市场之后,需要学习了解伦敦金相关规则,学习一定的做单的技巧,这样有利于我们后续做单顺畅盈利。以下总结几点安全…...
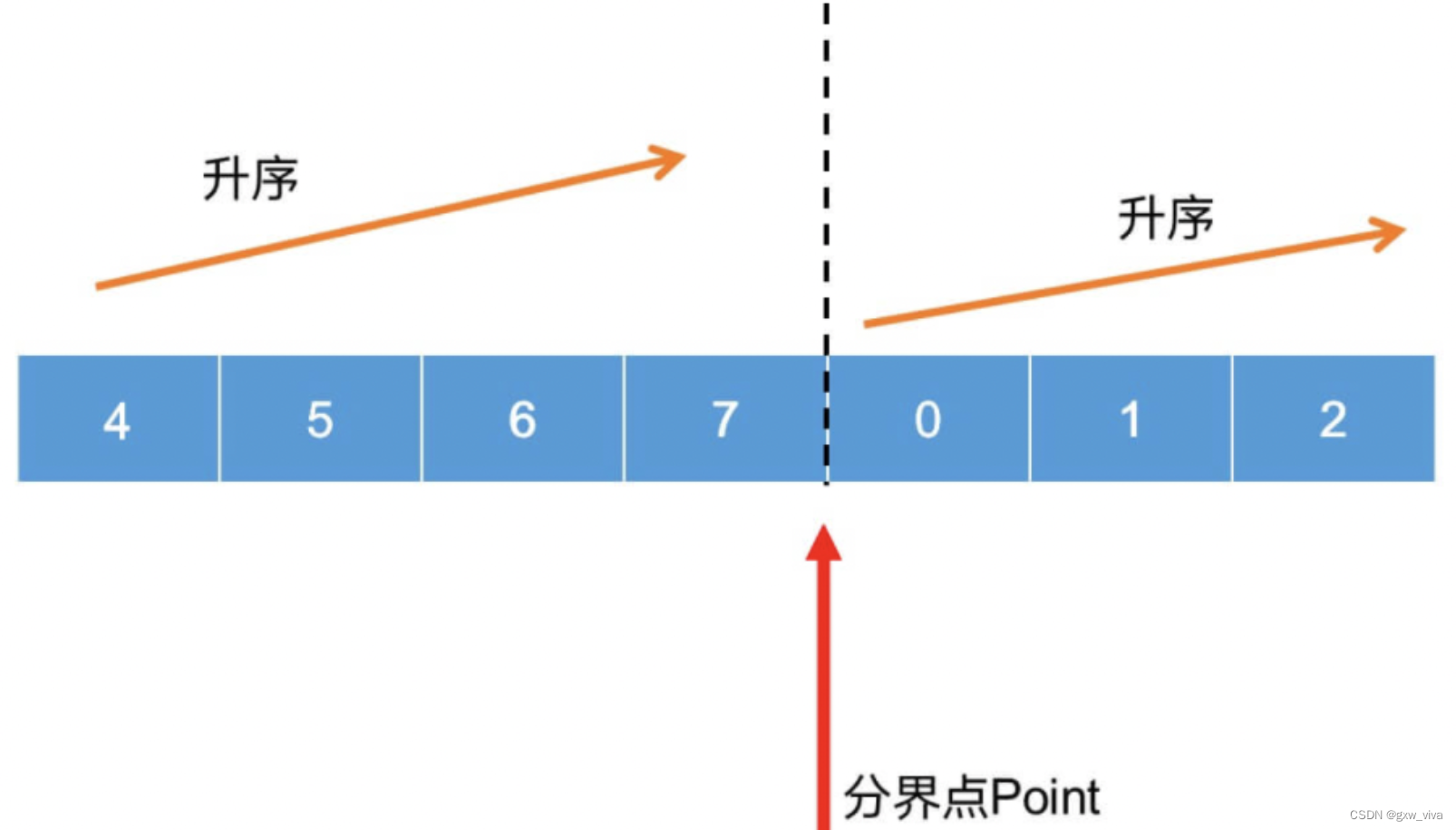
二分查找的理解及应用场景。
一、是什么 在计算机科学中,二分查找算法,也称折半搜索算法,是一种在有序数组中查找某一特定元素的搜索算法 想要应用二分查找法,则这一堆数应有如下特性: 存储在数组中有序排序 搜索过程从数组的中间元素开始&…...
共创时代,品牌如何做好UGC营销?
在当下的互联网时代,众多品牌已经逐渐意识到“产品为重”的影响方式已经很难提升转化率,内容才是吸引用户的必胜法宝,然而当代人被海量信息裹挟,人们的注意力成为稀缺资源,在这个环境下,UGC成为品牌的营销方…...
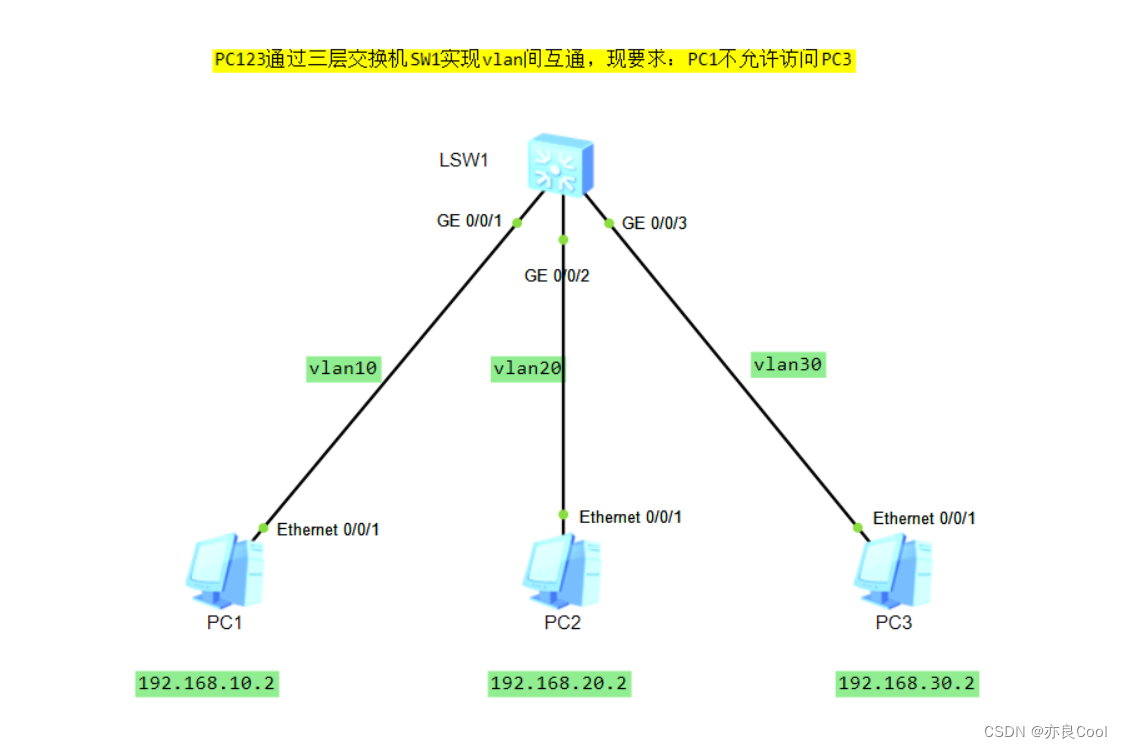
华为三层交换机:ACL的基本实验
实验要求: PC1不允许访问PC3,PC3可以访问PC1 分析问题: PC1不允许访问PC3,问题中含有“目标地址”则我们需要设置目标地址,这样基本ACL是不行的,必须使用高级ACL [sw1]acl ? INTEGER<2000-2999>…...
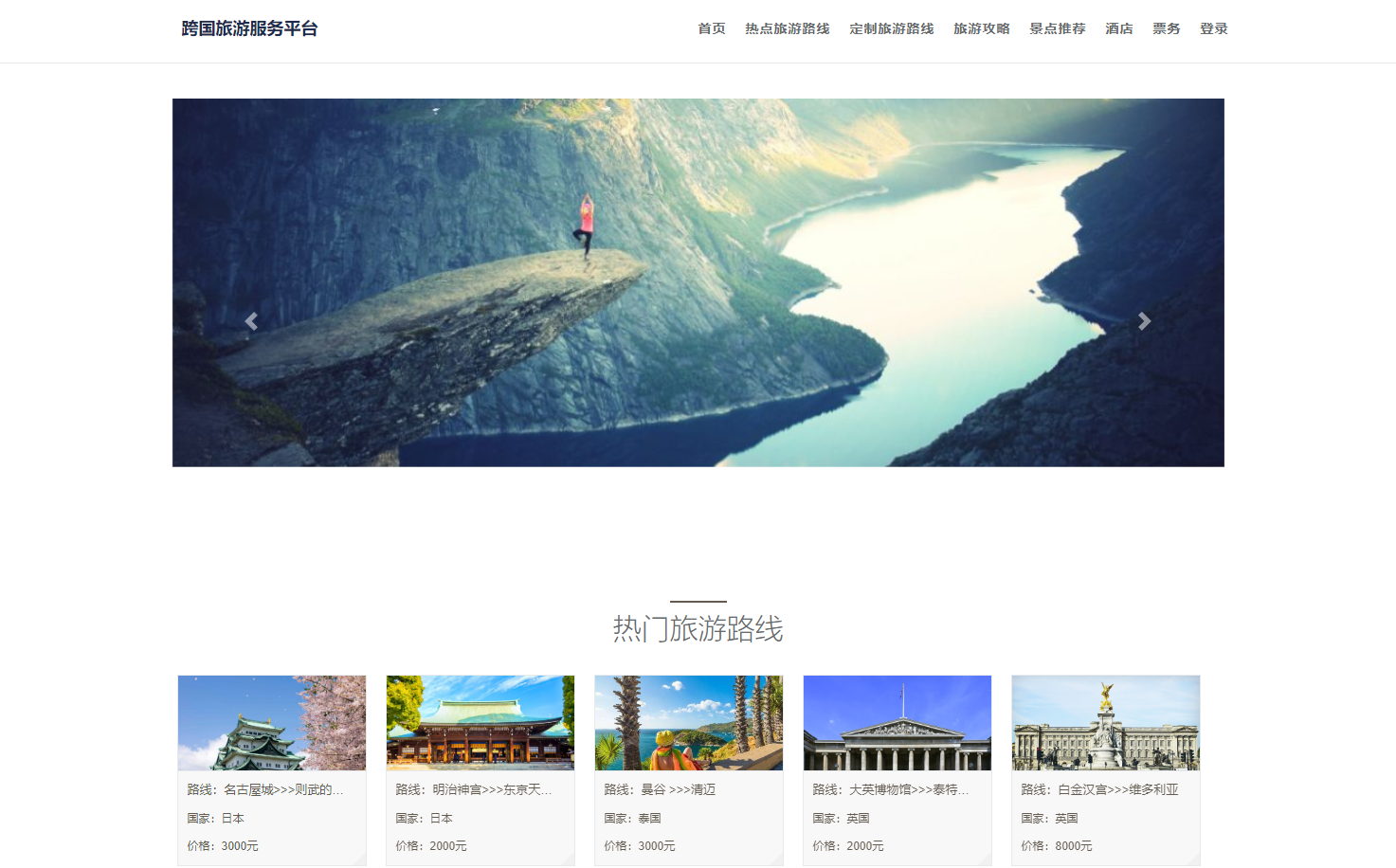
基于springboot+vue的旅游管理系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…...

4. git 添加版本标签
要给某一分支的某一提交版本添加标签(tag),你首先需要确定该提交版本在分支上的具体哈希值(commit hash)。 一旦你有了这个哈希值,你就可以像之前描述的那样使用 git tag 命令来创建标签。 以下是如何操作的…...
2024 PhpStorm激活,分享几个PhpStorm激活的方案
文章目录 PhpStorm 公司简介我这边使用PhpStorm的理由PhpStorm 2023.3 最新变化AI Assistant 预览阶段结束 正式版基于 LLM 的代码补全测试代码生成编辑器内代码生成控制台中基于 AI 的错误解释 Pest 更新PHP 8.3 支持#[\Override] 特性新的 json_validate() 函数类型化类常量弃…...
)
2419. prufer序列(prufer编码,模板题)
活动 - AcWing 本题需要你实现prufer序列与无根树之间的相互转化。 假设本题涉及的无根树共有 n 个节点,编号 1∼n。 为了更加简单明了的描述无根树的结构,我们不妨在输入和输出时将该无根树描述为一个以 n 号节点为根的有根树。 这样就可以设这棵无…...

鸿蒙Harmony应用开发—ArkTS声明式开发(基础手势:Text)
显示一段文本的组件。 说明: 该组件从API Version 7开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 子组件 可以包含Span和ImageSpan子组件。 接口 Text(content?: string | Resource, value?: TextOptions) 从API versi…...

开源大数据集群部署(十五)Zookeeper集群部署
作者:櫰木 1、集群规划 主机版本角色系统用户hd1.dtstack.com3.7.1followerzookeeperhd2.dtstack.com3.7.1leaderzookeeperhd3.dtstack.com3.7.1followerzookeeper 2、zookeeper kerberos主体创建 在生产中zk服务端和客户端票据可以设置成不通名称或相同名称&am…...

服务器镜像是什么
镜像即镜像服务器。镜像服务器与主服务器的服务内容都是一样的,只是放在一个不同的地方,分担主服务器的负载量。 可以使用,但不是原版的。在网上内容完全相同而且同步更新的两个或多个服务器,除主服务器外,其余的都被称…...
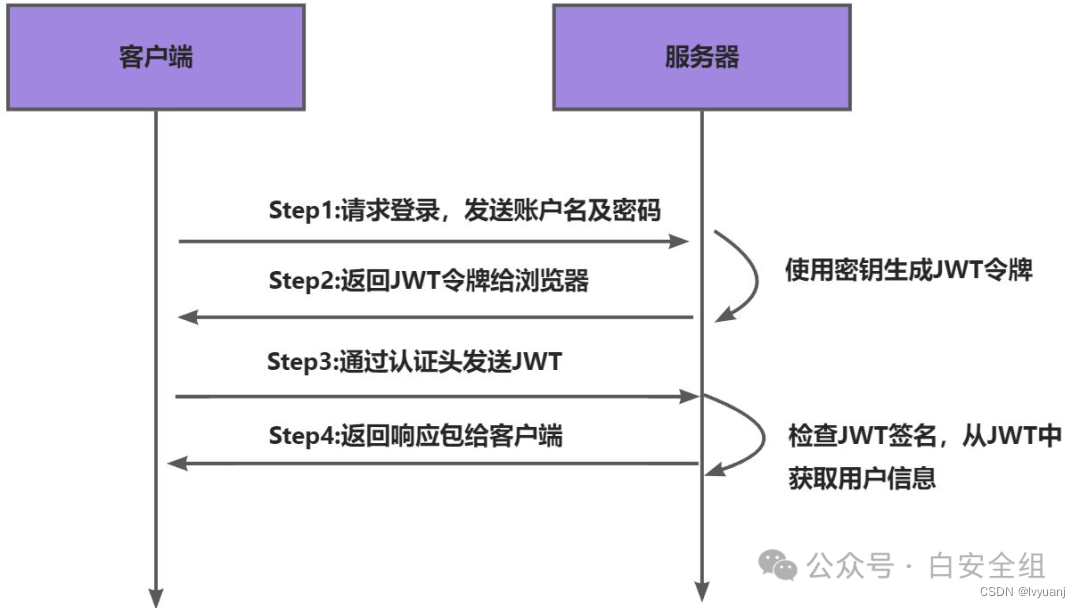
JWT原理
JWT 介绍 JWT(JSON Web Token)是一个开放标准(RFC 7519),它定义了一种简洁的、自包含的方法用于通信双方之间以 JSON 对象的形式安全地传输信息。这种信息可以被验证和信任,因为它是数字签名的。JWT通常用于…...

操作系统:一款纯正的“管理”软件
目录 前言: 1.操作系统的概念 2.操作系统的结构示意图: 3.什么是接口? 4.什么是驱动程序? 4.什么是系统调用(system call)? 5.操作系统和操作系统内核的区别 6.设计OS的核心目的 前言&…...

Mac笔记本聚焦SpotLight占用内存太高的 解法
分享一个自创的绝对有效的解决苹果电脑Mac笔记本SpotLight聚焦占用内存过高的方法! 一、背景 / 问题原因 1、Mac的聚焦功能,可以快速打开应用程序,非常方便! But,随着电脑的使用文件等越来越多,就会导致SpotLight聚焦需要更多更多甚至巨多的内存来建立索引,就会导致电脑…...

C++中.h和.hpp文件有什么区别?
在C中,.h和.hpp文件都是用于包含函数声明、类定义、宏定义等内容的头文件,它们的主要区别在于约定和习惯。 历史与来源:.h后缀是C语言头文件的标准后缀,随着C的演变,一些开发者开始使用.hpp后缀来表示C头文件ÿ…...

MongoDB聚合运算符:$derivative
$derivative聚合运算符返回返回指定窗口内的平均变化率(即求导),变化率使用以下公式计算: $setWindowFields阶段窗口中的第一个和最后一个文件。分子,等于最后一个文档的表达式的值减去第一个文档表达式的值。分母&am…...

面试官:如果你现在有20个Spring Boot微服务,如何监视所有这些Spring Boot微服务?
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:如果你现在有20个Spring Boot微服务,如何监视这些微服务? 要监视所有 Spring Boot 微服务,可以使用 Spring Boot Admin 这样的监控工具。Sprin…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
