2419. prufer序列(prufer编码,模板题)
活动 - AcWing
本题需要你实现prufer序列与无根树之间的相互转化。
假设本题涉及的无根树共有 n 个节点,编号 1∼n。
为了更加简单明了的描述无根树的结构,我们不妨在输入和输出时将该无根树描述为一个以 n 号节点为根的有根树。
这样就可以设这棵无根树的父亲序列为 f1,f2,…,fn−1,其中 fi 表示将该树看作以 n 号节点为根的有根树时,i 号节点的父节点编号。
同时,设这棵无根树的prufer序列为 p1,p2,…,pn−2。
现在,给定一棵由 n 个节点构成的无根树,以及该无根树的一个序列(父亲序列或prufer序列),请你求出另一个序列。
输入格式
输入共两行。
第一行包含两个整数 n,m,表示无根树的节点数以及给定序列类型。
如果 m=1,则第二行包含 n−1 个整数,表示给定序列为父亲序列。
如果 m=2,则第二行包含 n−2 个整数,表示给定序列为prufer序列。
输出格式
共一行,输出另一个序列,整数之间用单个空格隔开。
数据范围
2≤n≤10^5
输入样例1:
6 1
3 5 4 5 6
输出样例1:
3 5 4 5
输入样例2:
6 2
3 5 4 5
输出样例2:
3 5 4 5 6解析:
prufer编码主要作用即将一棵无根树转化为一个序列(即prufer序列),另外prufer序列也可以反过来转化为一棵树,即prufer序列和树之间是一一对应的,常用来解决一些证明问题,如凯莱定理等
证明凯莱定理(一个无向完全图有 n^(n−2) 棵生成树):由于prufer序列和树之间是一一对应的关系,证明有多少棵不同的生成树即证明有多少种prufer序列,显然,prufer序列共有 n−2 项,其范围为 1∼n,故其种类数为 n^(n−2)
prufer编码的流程:假定 n 号节点为根,找到除根外度数最小的节点,在删除该节点之前,将其父节点输出,重复该流程,直到最后只剩下两个节点,即prufer序列只有 n−2 个元素,因为prufer序列最多 n−1 个元素,而最后一个元素一定为 n,所以这个元素可以省略,输出的元素即为prufer序列
如何将一棵树线性时间内转化为prufer序列?
假定当前出度为 0 且编号最小的节点为 j,则输出 f[j],删除 j 之后,出度为 0 的节点至多只会增加一个,即 f[j],判断删除 j 之后 f[j] 的出度是否为 0,如果 f[j] 的出度为 0 且 f[j]<j 说明 f[j] 是当前出度为 0 且编号最小的节点,递归输出这样的父节点即可,否则说明这样的 j 只会更大,即 j 只会增加,这样即可线性时间内将一颗树转化为prufer序列
如何将一个prufer序列转化为一棵树?
先将 n 这个节点加入到prufer序列中,不难发现,prufer序列中某个数出现的次数即为该数在树中的儿子节点的数量,从 1 开始找到儿子数量为 0 且编号最小的节点 j,其父节点即为当前遍历的prufer序列的元素,将该元素从prufer序列中删去,因为删除该元素后儿子数量为 0 的节点数量至多直接增加一个,如果该元素的儿子数量为 0 且编号小于 j,说明当前节点即为儿子数量为 0 且编号最小的节点,递归处理即可,这样的 j 同样也是递增的,故可以在线性时间内将一个prufer序列转化为一棵树
时间复杂度:O(n)
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
#include<unordered_set>
#include<bitset>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
typedef pair<double, double> PDD;
const int N = 1e5 + 10, M = 1e4 + 10;
const double INF = 1e8;
int n, m;
int f[N], d[N], p[N];void tree2prufer() {for (int i = 1; i < n; i++) {scanf("%d", &f[i]);d[f[i]]++;}for (int i = 1, j = 1; i < n - 1; j++) {while (d[j])j++;p[i++] = f[j];while (i < n - 1 && --d [p[i-1]] == 0 && p[i - 1] < j)p[i++] = f[p[i - 1]];}for (int i = 1; i < n-1; i++) {printf("%d ", p[i]);}
}void prufer2tree() {for (int i = 1; i <= n-2; i++) {scanf("%d", &p[i]);d[p[i]]++;}p[n - 1] = n;for (int i = 1, j = 1; i < n; j++, i++) {while (d[j])j++;f[j] = p[i];while (i < n && --d[p[i]] == 0 && p[i] < j)f[p[i]] = p[i + 1], i++;}for (int i = 1; i < n; i++) {printf("%d ", f[i]);}
}int main() {cin >> n >> m;if (m == 1)tree2prufer();else prufer2tree();return 0;
}相关文章:
)
2419. prufer序列(prufer编码,模板题)
活动 - AcWing 本题需要你实现prufer序列与无根树之间的相互转化。 假设本题涉及的无根树共有 n 个节点,编号 1∼n。 为了更加简单明了的描述无根树的结构,我们不妨在输入和输出时将该无根树描述为一个以 n 号节点为根的有根树。 这样就可以设这棵无…...

鸿蒙Harmony应用开发—ArkTS声明式开发(基础手势:Text)
显示一段文本的组件。 说明: 该组件从API Version 7开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 子组件 可以包含Span和ImageSpan子组件。 接口 Text(content?: string | Resource, value?: TextOptions) 从API versi…...

开源大数据集群部署(十五)Zookeeper集群部署
作者:櫰木 1、集群规划 主机版本角色系统用户hd1.dtstack.com3.7.1followerzookeeperhd2.dtstack.com3.7.1leaderzookeeperhd3.dtstack.com3.7.1followerzookeeper 2、zookeeper kerberos主体创建 在生产中zk服务端和客户端票据可以设置成不通名称或相同名称&am…...

服务器镜像是什么
镜像即镜像服务器。镜像服务器与主服务器的服务内容都是一样的,只是放在一个不同的地方,分担主服务器的负载量。 可以使用,但不是原版的。在网上内容完全相同而且同步更新的两个或多个服务器,除主服务器外,其余的都被称…...
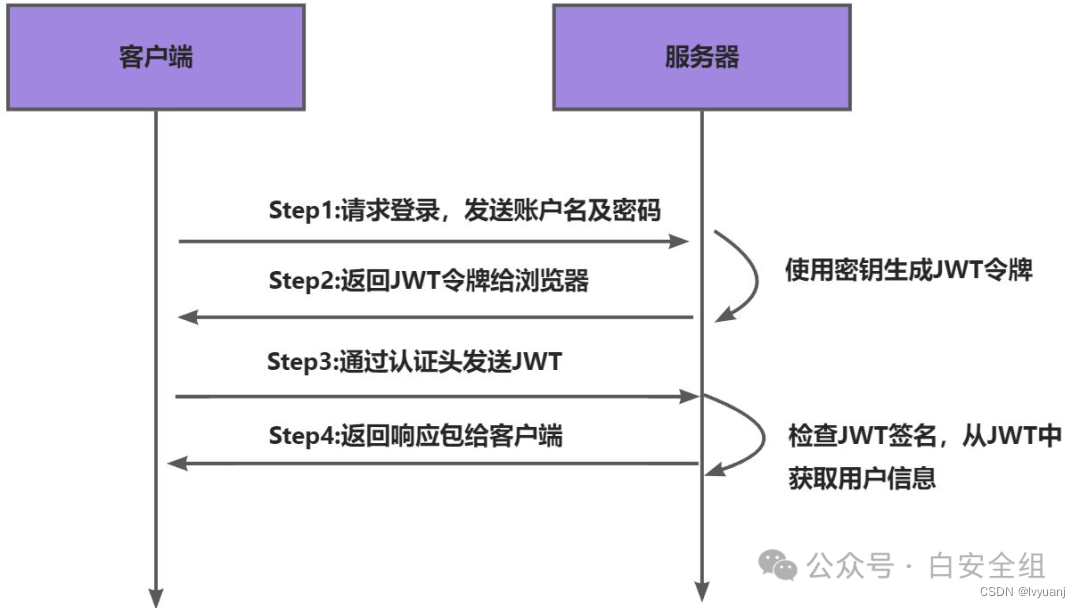
JWT原理
JWT 介绍 JWT(JSON Web Token)是一个开放标准(RFC 7519),它定义了一种简洁的、自包含的方法用于通信双方之间以 JSON 对象的形式安全地传输信息。这种信息可以被验证和信任,因为它是数字签名的。JWT通常用于…...

操作系统:一款纯正的“管理”软件
目录 前言: 1.操作系统的概念 2.操作系统的结构示意图: 3.什么是接口? 4.什么是驱动程序? 4.什么是系统调用(system call)? 5.操作系统和操作系统内核的区别 6.设计OS的核心目的 前言&…...

Mac笔记本聚焦SpotLight占用内存太高的 解法
分享一个自创的绝对有效的解决苹果电脑Mac笔记本SpotLight聚焦占用内存过高的方法! 一、背景 / 问题原因 1、Mac的聚焦功能,可以快速打开应用程序,非常方便! But,随着电脑的使用文件等越来越多,就会导致SpotLight聚焦需要更多更多甚至巨多的内存来建立索引,就会导致电脑…...

C++中.h和.hpp文件有什么区别?
在C中,.h和.hpp文件都是用于包含函数声明、类定义、宏定义等内容的头文件,它们的主要区别在于约定和习惯。 历史与来源:.h后缀是C语言头文件的标准后缀,随着C的演变,一些开发者开始使用.hpp后缀来表示C头文件ÿ…...

MongoDB聚合运算符:$derivative
$derivative聚合运算符返回返回指定窗口内的平均变化率(即求导),变化率使用以下公式计算: $setWindowFields阶段窗口中的第一个和最后一个文件。分子,等于最后一个文档的表达式的值减去第一个文档表达式的值。分母&am…...

面试官:如果你现在有20个Spring Boot微服务,如何监视所有这些Spring Boot微服务?
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:如果你现在有20个Spring Boot微服务,如何监视这些微服务? 要监视所有 Spring Boot 微服务,可以使用 Spring Boot Admin 这样的监控工具。Sprin…...
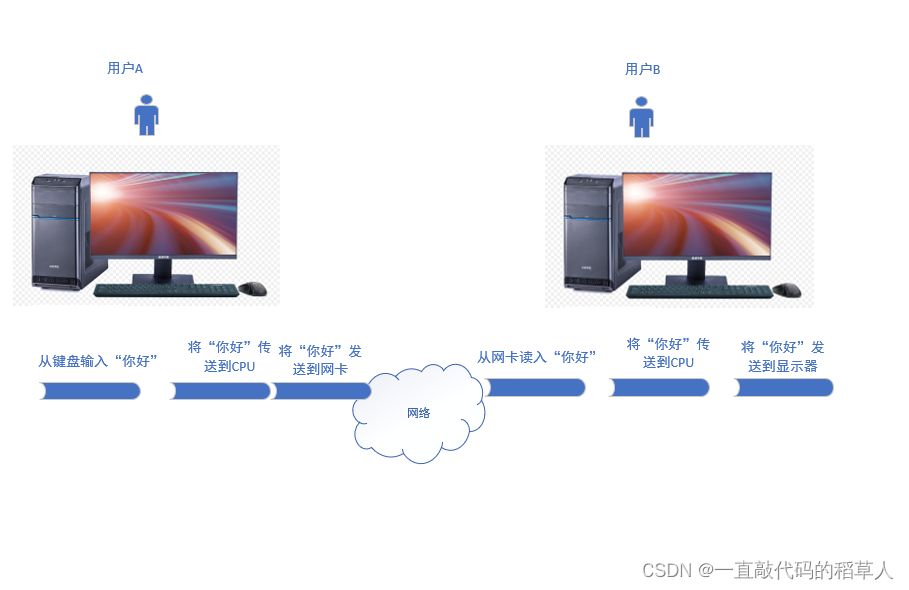
冯诺依曼模型
只要我们学习计算机操作系统,就离不开对冯诺依曼体系结构。因为我们常见的计算机,如笔记本。我们不常见的计算机,如服务器,大部分都遵守冯诺依曼体系。 1.什么是冯诺依曼模型呢? 如上图所示,冯诺依曼模型由…...

高低拖延个体的任务决策及执行差异
高低拖延个体的任务决策及执行差异 摘要 拖延行为普遍存在,且影响着许多人的工作.学习和生活。已有的许多研究发现拖延个体明知自己需要尽快完成某项任务,但行动上却迟迟无法付诸实践,表现出一种知行不- -”的倾向.这种倾向是否在高低拖延特质者之间存…...
>)
数据分析Pandas专栏---第十三章<Pandas训练题(初)>
前言: 写这篇是为了弄一个富有挑战性的Pandas练习题库,涵盖了许多常见和实用的数据处理问题。通过解决这些练习,能够深入了解Pandas提供的关键功能,掌握有效处理数据的技巧和方法。 练习题库涵盖了选择特定列并创建新DataFrame、对DataFrame进…...
 错误的解决方案)
Delete `␍`eslint(prettier/prettier) 错误的解决方案
最近开始一个新的项目,由他人构建,clone下来后,发现页面每行都有黄色的波浪线的提示:Delete ␍eslint(prettier/prettier) ,尝试了很多方法不能解决,最后选择关闭Prettier: 在.eslintrc.js文件…...

第3周 Python字典、集合刷题
第3周 Python字典、集合刷题 单击题目,直接跳转到页面刷题,一周后公布答案。 B2125:最高分数的学生姓名28:返回字典的键值75:字符串转字典77:映射字符串中的字母87:按条件过滤字典B3632&#…...
文字校对的首选——爱校对:用户真实反馈汇编
在今日快节奏、高标准的工作环境下,准确与效率成为了每位专业人士追求的双重目标。不论是在政府机构、学术领域、企业界,还是在自由职业者的行列中,我们都面临着同一个挑战:如何在保持工作速度的同时,确保每一份文档的…...

Llama-3即将发布:Meta公布其庞大的AI算力集群
Meta,这家全球科技巨头,再次以其在人工智能(AI)领域的雄心壮志震惊了世界。3月13日,公司在其官方网站上宣布了两个全新的24K H100 GPU集群,这些集群专为训练其大型模型Llama-3而设计,总计拥有高…...

【JAVA】Date、LocalDate、LocalDateTime 详解,实践应用
Date、LocalDate、LocalDateTime 详解,实践应用 一、Date、LocalDate 简介1、 java.util.Date:2、 java.time.LocalDateTime:3、 java.time.LocalDate: 二、输出格式1、使用 java.util.Date 的示例代码如下:2、使用 ja…...

分布式链路追踪(一)SkyWalking(1)介绍与安装
一、介绍 1、简介: 2、组成 以6.5.0为例,该版本下Skywalking主要分为oap、webapp和agent三部分,oap和webapp分别用于汇总数据和展示,这两块共同组成了Skywalking的平台;agent是探针,部署在需要收集数据的…...

蓝桥杯历年真题省赛之 2016年 第七届 生日蜡烛
一、题目 生日蜡烛 某君从某年开始每年都举办一次生日party,并且每次都要吹熄与年龄相同根数的蜡烛。 现在算起来,他一共吹熄了236根蜡烛。 请问,他从多少岁开始过生日party的? 请填写他开始过生日party的年龄数。 注意&…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
