二分查找的理解及应用场景。
一、是什么
在计算机科学中,二分查找算法,也称折半搜索算法,是一种在有序数组中查找某一特定元素的搜索算法
想要应用二分查找法,则这一堆数应有如下特性:
- 存储在数组中
- 有序排序
搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束
如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较,如果在某一步骤数组为空,则代表找不到,这种搜索算法每一次比较都使搜索范围缩小一半。

相比普通的顺序查找,除了数据量很少的情况下,二分查找会比顺序查找更快。
二、如何实现
基于二分查找的实现,如果数据是有序的,并且不存在重复项,实现代码如下:
function BinarySearch(arr, target) {if (arr.length <= 1) return -1// 低位下标let lowIndex = 0// 高位下标let highIndex = arr.length - 1while (lowIndex <= highIndex) {// 中间下标const midIndex = Math.floor((lowIndex + highIndex) / 2)if (target < arr[midIndex]) {highIndex = midIndex - 1} else if (target > arr[midIndex]) {lowIndex = midIndex + 1} else {// target === arr[midIndex]return midIndex}}return -1
}如果数组中存在重复项,而我们需要找出第一个制定的值,实现则如下:
function BinarySearchFirst(arr, target) {if (arr.length <= 1) return -1// 低位下标let lowIndex = 0// 高位下标let highIndex = arr.length - 1while (lowIndex <= highIndex) {// 中间下标const midIndex = Math.floor((lowIndex + highIndex) / 2)if (target < arr[midIndex]) {highIndex = midIndex - 1} else if (target > arr[midIndex]) {lowIndex = midIndex + 1} else {// 当 target 与 arr[midIndex] 相等的时候,如果 midIndex 为0或者前一个数比 target 小那么就找到了第一个等于给定值的元素,直接返回if (midIndex === 0 || arr[midIndex - 1] < target) return midIndex// 否则高位下标为中间下标减1,继续查找highIndex = midIndex - 1}}return -1
}实际上,除了有序的数组可以使用,还有一种特殊的数组可以应用,那就是轮转后的有序数组
有序数组即一个有序数字以某一个数为轴,将其之前的所有数都轮转到数组的末尾所得
例如,[4, 5, 6, 7, 0, 1, 2]就是一个轮转后的有序数组
该数组的特性是存在一个分界点用来分界两个有序数组,如下:
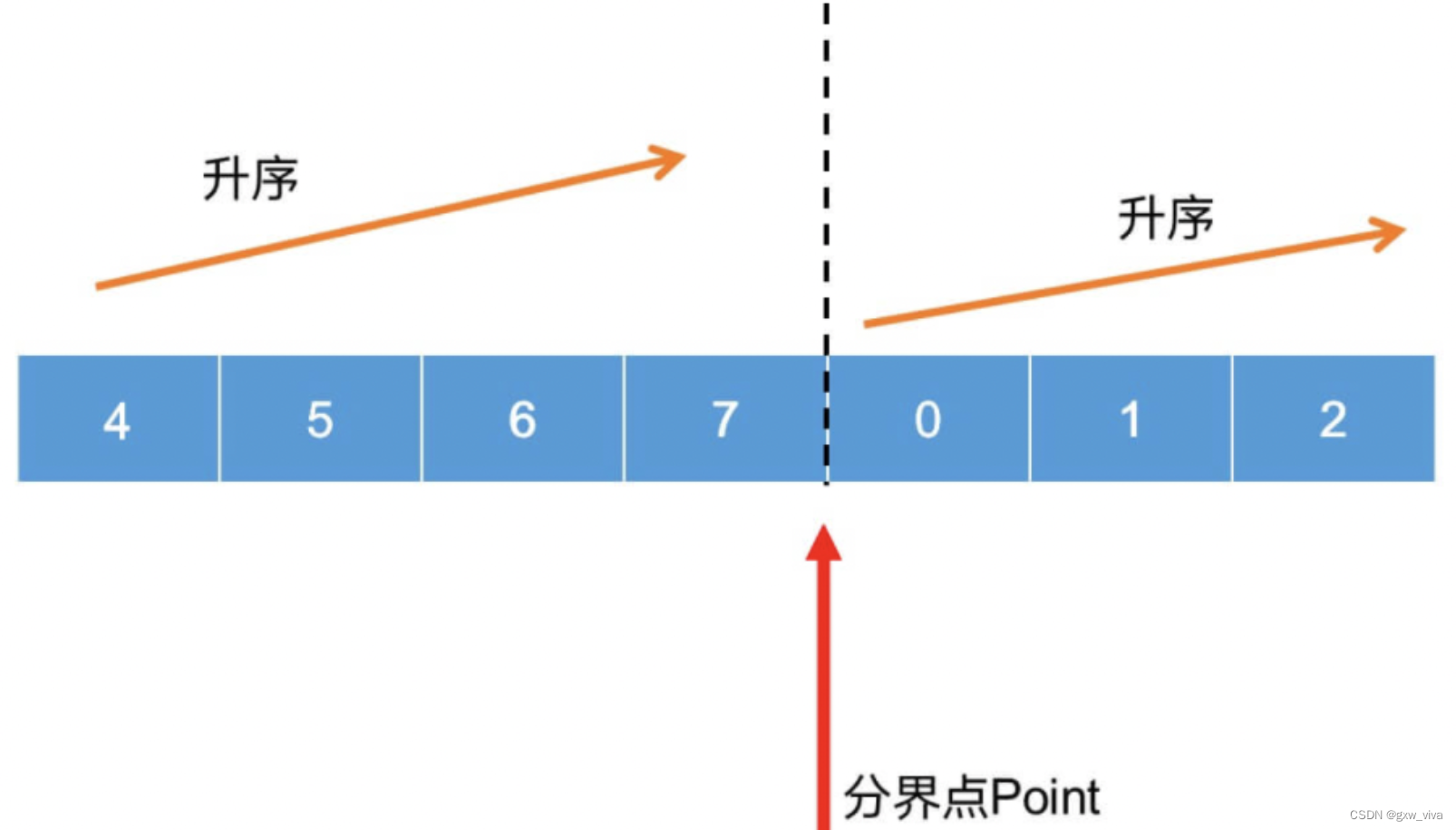
分界点有如下特性:
- 分界点元素 >= 第一个元素
- 分界点元素 < 第一个元素
代码实现如下:
function search (nums, target) {// 如果为空或者是空数组的情况if (nums == null || !nums.length) {return -1;}// 搜索区间是前闭后闭let begin = 0,end = nums.length - 1;while (begin <= end) {// 下面这样写是考虑大数情况下避免溢出let mid = begin + ((end - begin) >> 1);if (nums[mid] == target) {return mid;}// 如果左边是有序的if (nums[begin] <= nums[mid]) {//同时target在[ nums[begin],nums[mid] ]中,那么就在这段有序区间查找if (nums[begin] <= target && target <= nums[mid]) {end = mid - 1;} else {//否则去反方向查找begin = mid + 1;}//如果右侧是有序的} else {//同时target在[ nums[mid],nums[end] ]中,那么就在这段有序区间查找if (nums[mid] <= target && target <= nums[end]) {begin = mid + 1;} else {end = mid - 1;}}}return -1;
};对比普通的二分查找法,为了确定目标数会落在二分后的哪个部分,我们需要更多的判定条件。
三、应用场景
二分查找法的O(logn)让它成为十分高效的算法。不过它的缺陷却也是比较明显,就在它的限定之上:
- 有序:我们很难保证我们的数组都是有序的
- 数组:数组读取效率是O(1),可是它的插入和删除某个元素的效率却是O(n),并且数组的存储是需要连续的内存空间,不适合大数据的情况
关于二分查找的应用场景,主要如下:
- 不适合数据量太小的数列;数列太小,直接顺序遍历说不定更快,也更简单
- 每次元素与元素的比较是比较耗时的,这个比较操作耗时占整个遍历算法时间的大部分,那么使用二分查找就能有效减少元素比较的次数
- 不适合数据量太大的数列,二分查找作用的数据结构是顺序表,也就是数组,数组是需要连续的内存空间的,系统并不一定有这么大的连续内存空间可以使用
相关文章:

二分查找的理解及应用场景。
一、是什么 在计算机科学中,二分查找算法,也称折半搜索算法,是一种在有序数组中查找某一特定元素的搜索算法 想要应用二分查找法,则这一堆数应有如下特性: 存储在数组中有序排序 搜索过程从数组的中间元素开始&…...
共创时代,品牌如何做好UGC营销?
在当下的互联网时代,众多品牌已经逐渐意识到“产品为重”的影响方式已经很难提升转化率,内容才是吸引用户的必胜法宝,然而当代人被海量信息裹挟,人们的注意力成为稀缺资源,在这个环境下,UGC成为品牌的营销方…...
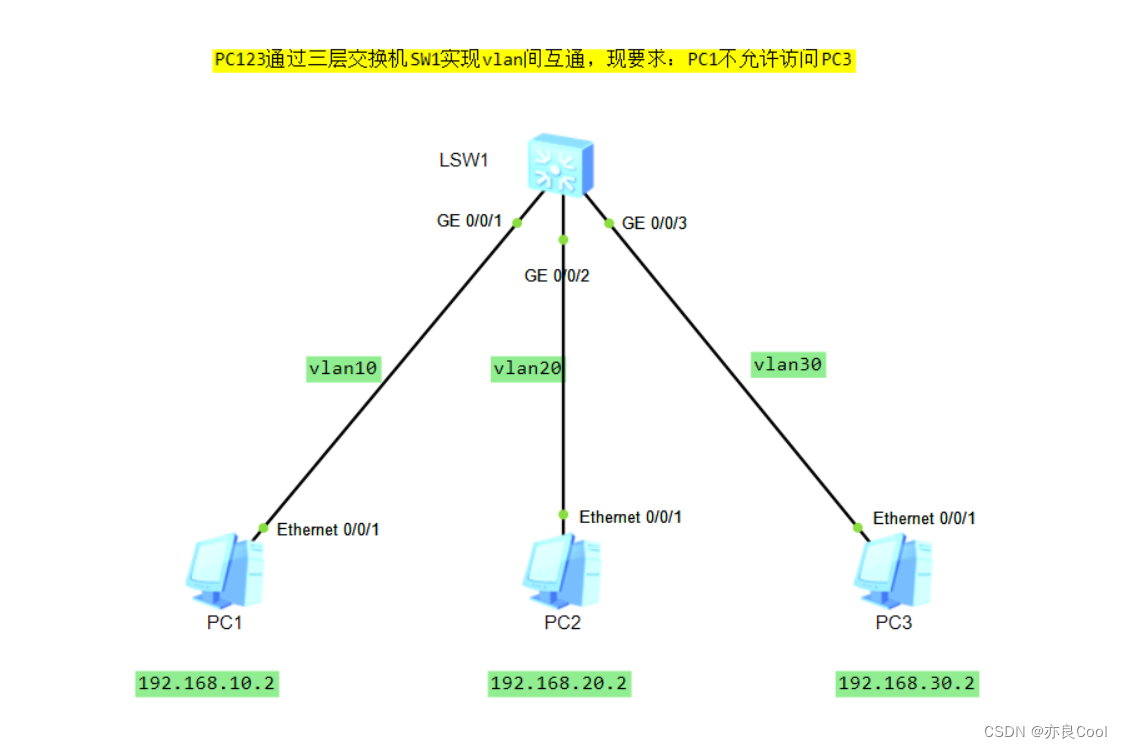
华为三层交换机:ACL的基本实验
实验要求: PC1不允许访问PC3,PC3可以访问PC1 分析问题: PC1不允许访问PC3,问题中含有“目标地址”则我们需要设置目标地址,这样基本ACL是不行的,必须使用高级ACL [sw1]acl ? INTEGER<2000-2999>…...
基于springboot+vue的旅游管理系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…...

4. git 添加版本标签
要给某一分支的某一提交版本添加标签(tag),你首先需要确定该提交版本在分支上的具体哈希值(commit hash)。 一旦你有了这个哈希值,你就可以像之前描述的那样使用 git tag 命令来创建标签。 以下是如何操作的…...
2024 PhpStorm激活,分享几个PhpStorm激活的方案
文章目录 PhpStorm 公司简介我这边使用PhpStorm的理由PhpStorm 2023.3 最新变化AI Assistant 预览阶段结束 正式版基于 LLM 的代码补全测试代码生成编辑器内代码生成控制台中基于 AI 的错误解释 Pest 更新PHP 8.3 支持#[\Override] 特性新的 json_validate() 函数类型化类常量弃…...
)
2419. prufer序列(prufer编码,模板题)
活动 - AcWing 本题需要你实现prufer序列与无根树之间的相互转化。 假设本题涉及的无根树共有 n 个节点,编号 1∼n。 为了更加简单明了的描述无根树的结构,我们不妨在输入和输出时将该无根树描述为一个以 n 号节点为根的有根树。 这样就可以设这棵无…...

鸿蒙Harmony应用开发—ArkTS声明式开发(基础手势:Text)
显示一段文本的组件。 说明: 该组件从API Version 7开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 子组件 可以包含Span和ImageSpan子组件。 接口 Text(content?: string | Resource, value?: TextOptions) 从API versi…...

开源大数据集群部署(十五)Zookeeper集群部署
作者:櫰木 1、集群规划 主机版本角色系统用户hd1.dtstack.com3.7.1followerzookeeperhd2.dtstack.com3.7.1leaderzookeeperhd3.dtstack.com3.7.1followerzookeeper 2、zookeeper kerberos主体创建 在生产中zk服务端和客户端票据可以设置成不通名称或相同名称&am…...

服务器镜像是什么
镜像即镜像服务器。镜像服务器与主服务器的服务内容都是一样的,只是放在一个不同的地方,分担主服务器的负载量。 可以使用,但不是原版的。在网上内容完全相同而且同步更新的两个或多个服务器,除主服务器外,其余的都被称…...
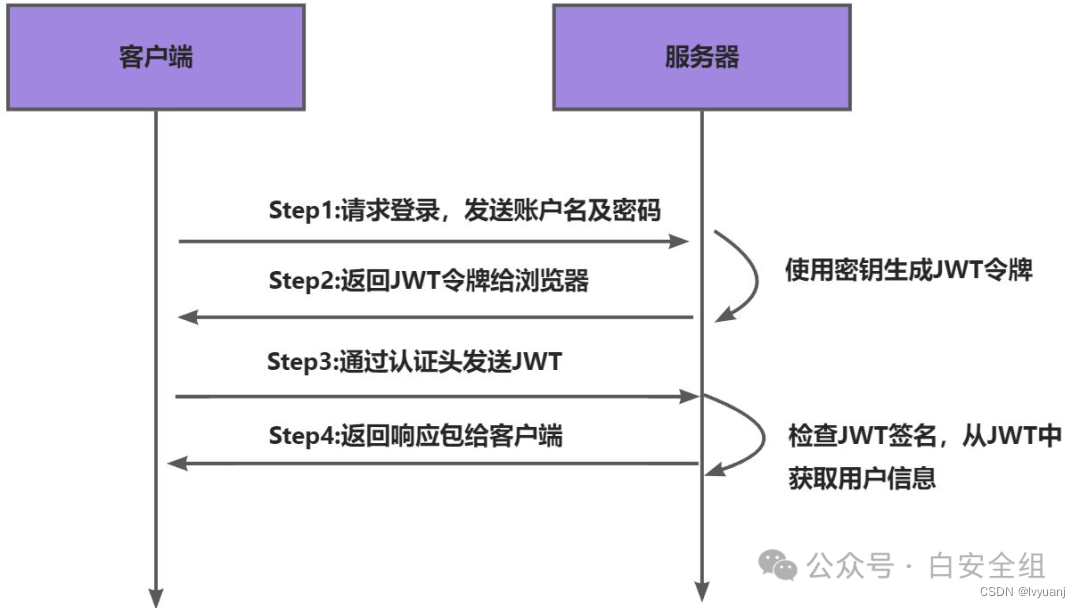
JWT原理
JWT 介绍 JWT(JSON Web Token)是一个开放标准(RFC 7519),它定义了一种简洁的、自包含的方法用于通信双方之间以 JSON 对象的形式安全地传输信息。这种信息可以被验证和信任,因为它是数字签名的。JWT通常用于…...

操作系统:一款纯正的“管理”软件
目录 前言: 1.操作系统的概念 2.操作系统的结构示意图: 3.什么是接口? 4.什么是驱动程序? 4.什么是系统调用(system call)? 5.操作系统和操作系统内核的区别 6.设计OS的核心目的 前言&…...

Mac笔记本聚焦SpotLight占用内存太高的 解法
分享一个自创的绝对有效的解决苹果电脑Mac笔记本SpotLight聚焦占用内存过高的方法! 一、背景 / 问题原因 1、Mac的聚焦功能,可以快速打开应用程序,非常方便! But,随着电脑的使用文件等越来越多,就会导致SpotLight聚焦需要更多更多甚至巨多的内存来建立索引,就会导致电脑…...

C++中.h和.hpp文件有什么区别?
在C中,.h和.hpp文件都是用于包含函数声明、类定义、宏定义等内容的头文件,它们的主要区别在于约定和习惯。 历史与来源:.h后缀是C语言头文件的标准后缀,随着C的演变,一些开发者开始使用.hpp后缀来表示C头文件ÿ…...

MongoDB聚合运算符:$derivative
$derivative聚合运算符返回返回指定窗口内的平均变化率(即求导),变化率使用以下公式计算: $setWindowFields阶段窗口中的第一个和最后一个文件。分子,等于最后一个文档的表达式的值减去第一个文档表达式的值。分母&am…...

面试官:如果你现在有20个Spring Boot微服务,如何监视所有这些Spring Boot微服务?
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:如果你现在有20个Spring Boot微服务,如何监视这些微服务? 要监视所有 Spring Boot 微服务,可以使用 Spring Boot Admin 这样的监控工具。Sprin…...
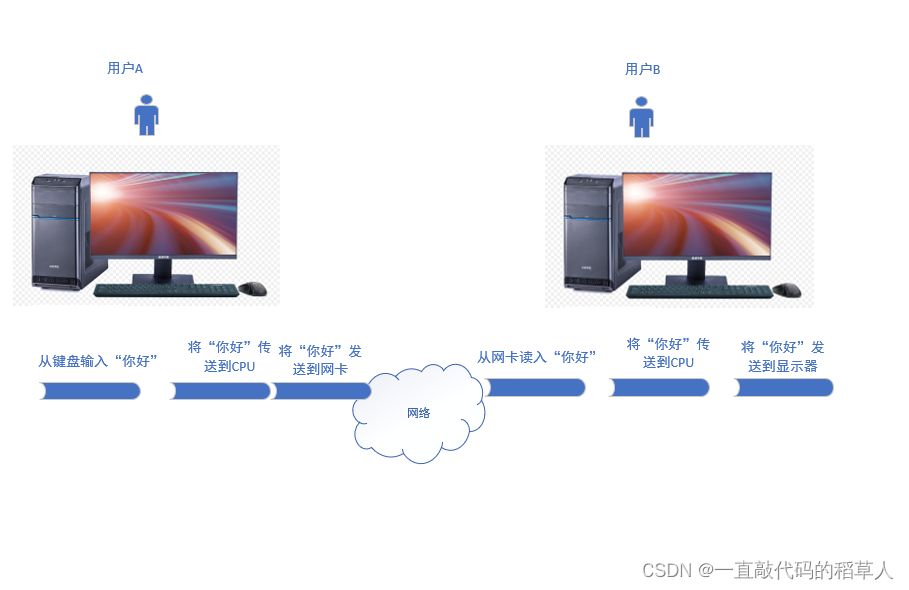
冯诺依曼模型
只要我们学习计算机操作系统,就离不开对冯诺依曼体系结构。因为我们常见的计算机,如笔记本。我们不常见的计算机,如服务器,大部分都遵守冯诺依曼体系。 1.什么是冯诺依曼模型呢? 如上图所示,冯诺依曼模型由…...

高低拖延个体的任务决策及执行差异
高低拖延个体的任务决策及执行差异 摘要 拖延行为普遍存在,且影响着许多人的工作.学习和生活。已有的许多研究发现拖延个体明知自己需要尽快完成某项任务,但行动上却迟迟无法付诸实践,表现出一种知行不- -”的倾向.这种倾向是否在高低拖延特质者之间存…...
>)
数据分析Pandas专栏---第十三章<Pandas训练题(初)>
前言: 写这篇是为了弄一个富有挑战性的Pandas练习题库,涵盖了许多常见和实用的数据处理问题。通过解决这些练习,能够深入了解Pandas提供的关键功能,掌握有效处理数据的技巧和方法。 练习题库涵盖了选择特定列并创建新DataFrame、对DataFrame进…...
 错误的解决方案)
Delete `␍`eslint(prettier/prettier) 错误的解决方案
最近开始一个新的项目,由他人构建,clone下来后,发现页面每行都有黄色的波浪线的提示:Delete ␍eslint(prettier/prettier) ,尝试了很多方法不能解决,最后选择关闭Prettier: 在.eslintrc.js文件…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
