2024年华为OD机试真题-查找众数及中位数-Java-OD统一考试(C卷)
题目描述:
众数是指一组数据中出现次数量多的那个数,众数可以是多个。
中位数是指把一组数据从小到大排列,最中间的那个数,如果这组数据的个数是奇数,那最中间那个就是中位数,如果这组数据的个数为偶数,那就把中间的两个数之和除以2,所得的结果就是中位数。
查找整型数组中元素的众数并组成一个新的数组,求新数组的中位数。
输入描述
输入一个一维整型数组,数组大小取值范围
0\<N<1000,数组中每个元素取值范围
0<E<1000
输出描述
输出众数组成的新数组的中位数
示例1
输入输出示例仅供调试,后台判题数据一般不包含示例
输入
10 11 21 19 21 17 21 16 21 18 15
输出
21
示例2
输入输出示例仅供调试,后台判题数据一般不包含示例
输入
2 1 5 4 3 3 9 2 7 4 6 2 15 4 2 4
输出
3
示例3
输入输出示例仅供调试,后台判题数据一般不包含示例
输入
5 1 5 3 5 2 5 5 7 6 7 3 7 11 7 55 7 9 98 9 17 9 15 9 9 1 39
输出
7
解题思路:考
相关文章:
)
2024年华为OD机试真题-查找众数及中位数-Java-OD统一考试(C卷)
题目描述: 众数是指一组数据中出现次数量多的那个数,众数可以是多个。 中位数是指把一组数据从小到大排列,最中间的那个数,如果这组数据的个数是奇数,那最中间那个就是中位数,如果这组数据的个数为偶数,那就把中间的两个数之和除以2,所得的结果就是中位数。 查找整型数…...
力扣思路题:重复的子字符串
注意比较j与j-i是否相同 bool repeatedSubstringPattern(char* s) {int i;int nstrlen(s);bool flag;for(int i1;i<n/2;i){if(n%i0){flagtrue;}for(int ji;j<n;j){if(s[j]!s[j-i]){flagfalse;break;}}if(flagtrue){return true;}}return false; }...

同城即配年度观察:顺丰同城率先全年盈利,行业破局迎参考
即时消费趋势增强,“万物到家即时可得”成为了消费新常态。这创造出不可忽视的场景潜力,也在无形中让龙头企业的发展质量走到突破点。 3月11日晚,“第三方即时配送第一股”顺丰同城发布公告称,预期实现2023年全年盈利,…...

线上机器 swap 过高导致告警
哈喽大家好,我是咸鱼。 今天收到了一个告警,说有台服务器上的 swap 过高,已经用了 50% 以上了。 登录机器查看一下内存以及 swap 的使用情况。 [rootlocalhost ~]# free -h total used free shared buff/cache ava…...
案例分析篇13:系统分析与设计考点(2024年软考高级系统架构设计师冲刺知识点总结系列文章)
专栏系列文章推荐: 2024高级系统架构设计师备考资料(高频考点&真题&经验)https://blog.csdn.net/seeker1994/category_12593400.html 【历年案例分析真题考点汇总】与【专栏文章案例分析高频考点目录】(2024年软考高级系统架构设计师冲刺知识点总结-案例分析篇-…...
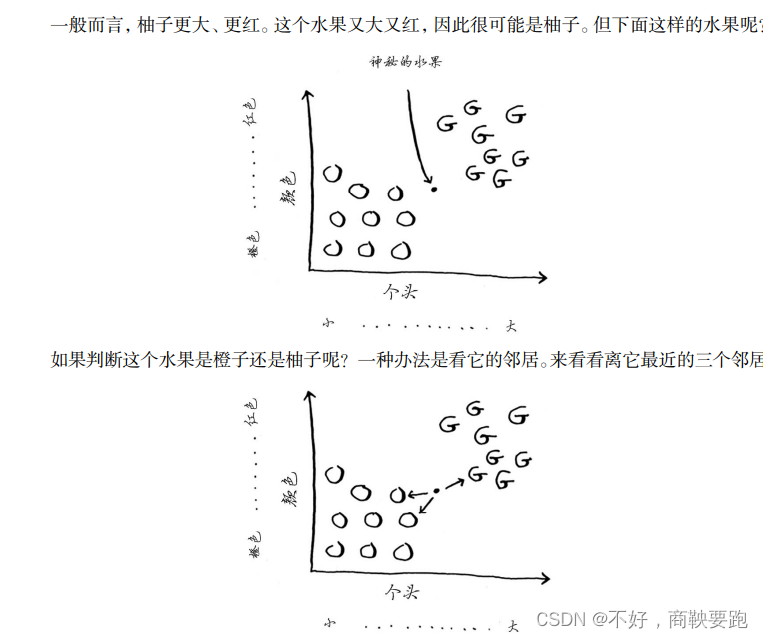
算法(结合算法图解)
算法简介简单查找二分查找法 选择排序内存的工作原理数组和链表数组选择排序小结 递归小梗 要想学会递归,首先要学会递归。 递归的基线条件和递归条件递归和栈小结 快速排序分而治之快速排序合并排序时间复杂度的平均情况和最糟情况小结 散列表散列函数缓冲小结性能…...

Linux-多线程
目录 线程概念线程控制创建退出等待join实例detach实例 实例 线程安全概念互斥同步生产者与消费者模型实例 信号量 线程应用 线程概念 线程概念: 有一个零件加工工厂,工厂中有一个或多个工人 工人是干活的,工厂是集体设备资源的载体 进程就是…...

深入解析C++树形关联式容器:map、set及其衍生容器的使用与原理
文章目录 一、引言二、关联式容器的中的 paira.pair 的创建及使用b.pair 间的比较 三、 map 与 set 详解1. map 的基本操作2. set 的基本操作3.关联式容器的迭代器 四、 multimap 与 multiset 的特性五、关联式容器的使用技巧与注意事项1. 键值类型的选择与设计2. 自定义比较函…...
)
c++基础知识(一)
C字符集:通常将一个标准中能够表示所有字符的一个集合称为字符集。例如Unicode字符集、ASCll、GB2312、BIG5(繁体中文及其相关字符)等。 字符集是组成程序设计语言的基本要素。由单字符、关键字、标识符、运算符(操作符ÿ…...

Midjourney绘图欣赏系列【人物篇】(一)
Midjourney介绍 Midjourney 是生成式人工智能的一个很好的例子,它根据文本提示创建图像。它与 Dall-E 和 Stable Diffusion 一起成为最流行的 AI 艺术创作工具之一。与竞争对手不同,Midjourney 是自筹资金且闭源的,因此确切了解其幕后内容尚不…...
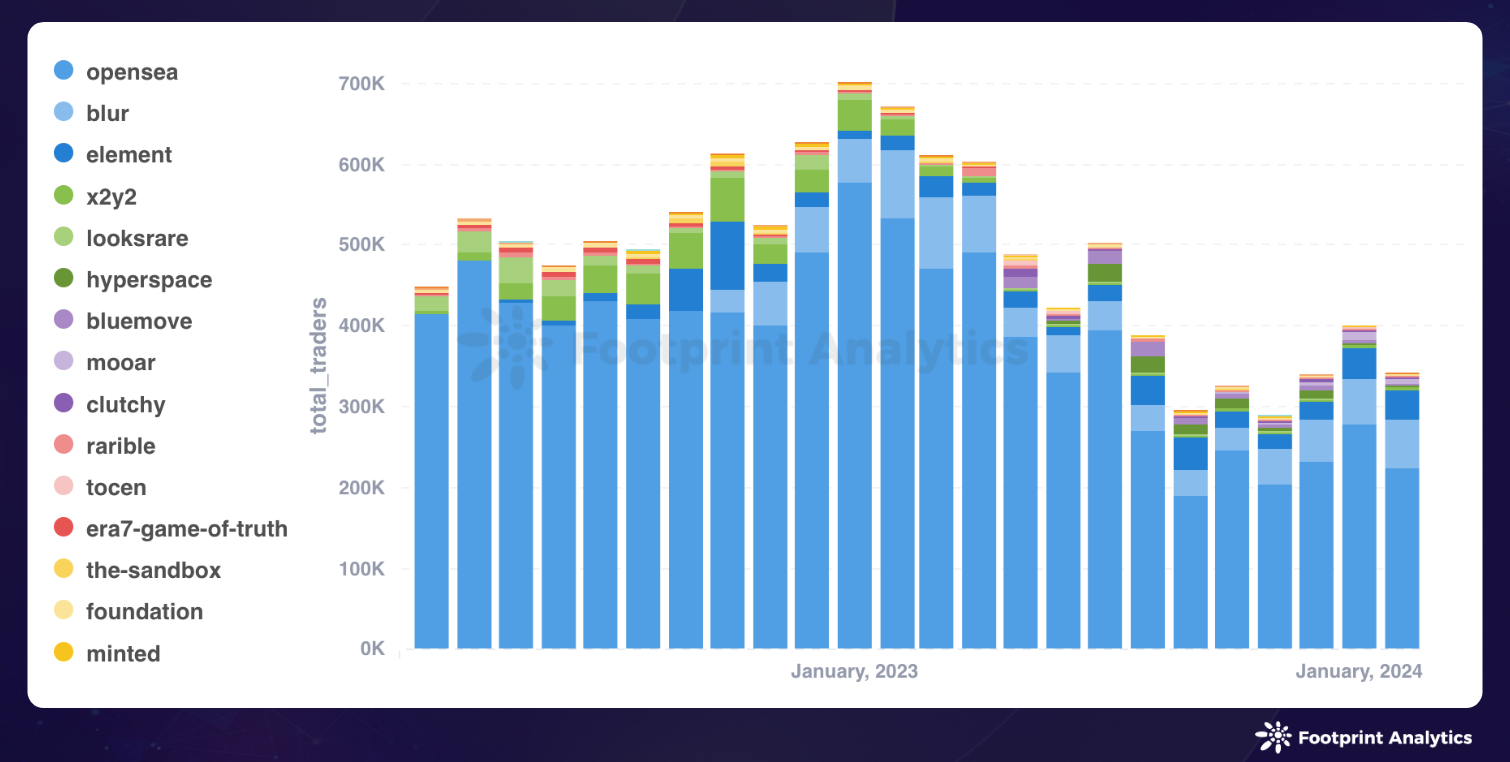
2024 年 2 月 NFT 行业动态:加密货币飙升,NFT 市场调整
作者:stellafootprint.network 数据来源:NFT 研究页面 - Footprint Analytics 2024 年 2 月,加密货币与 NFT 市场显现出了复杂性。该月,NFT 领域的交易量达到 12 亿美元,环比下降了 3.7%。值得关注的是,包…...
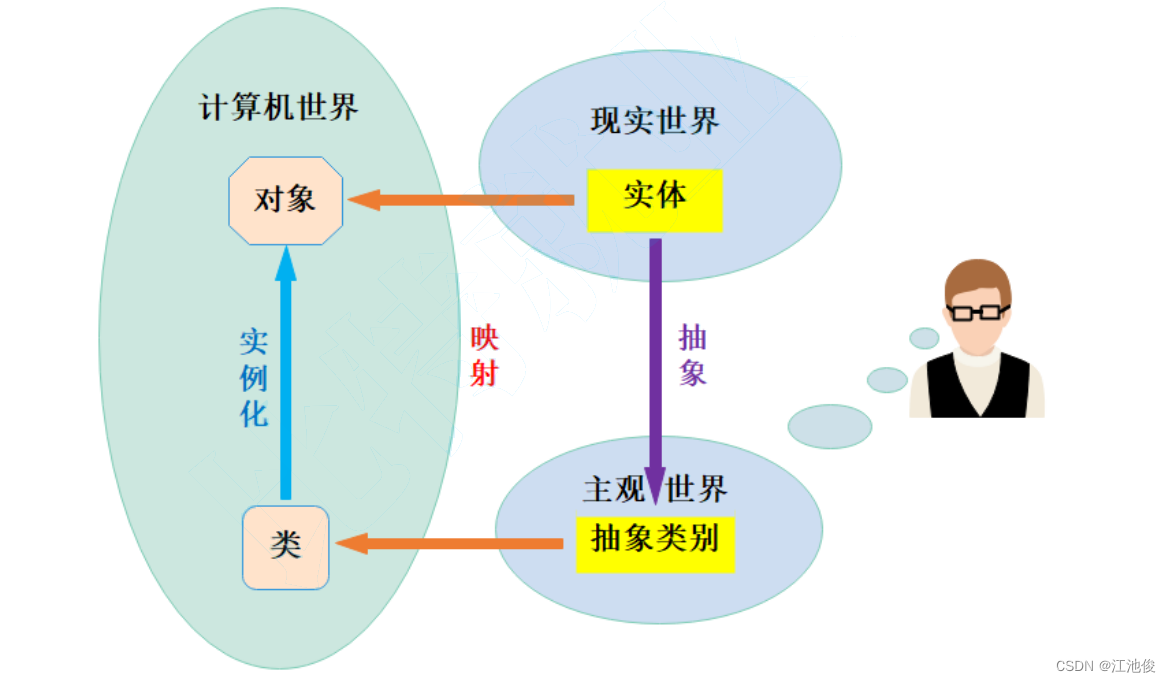
【C++那些事儿】深入理解C++类与对象:从概念到实践(下)| 再谈构造函数(初始化列表)| explicit关键字 | static成员 | 友元
📷 江池俊:个人主页 🔥 个人专栏:✅C那些事儿 ✅Linux技术宝典 🌅 此去关山万里,定不负云起之望 文章目录 1. 再谈构造函数1.1 构造函数体赋值1.2 初始化列表1.3 explicit 关键字 2. static成员2.1 概念…...

前端面试 ===> 【Vue2】
Vue2 相关面试题总结 1. 谈谈对Vue的理解 Vue是一种用于构建用户页面的渐进式JavaScript框架,也是一个创建SPA单页面应用的Web应用框架,Vue的核心是 数据驱动试图,通过组件内特定的方法实现视图和模型的交互;特性:&a…...

面试 Java 并发编程八股文十问十答第四期
面试 Java 并发编程八股文十问十答第四期 作者:程序员小白条,个人博客 相信看了本文后,对你的面试是有一定帮助的!关注专栏后就能收到持续更新! ⭐点赞⭐收藏⭐不迷路!⭐ 1)Java 中你怎样唤醒…...
)
物体检测-系列教程27:YOLOV5 源码解析17(训练脚本解读:训练函数4)
😎😎😎物体检测-系列教程 总目录 有任何问题欢迎在下面留言 本篇文章的代码运行界面均在Pycharm中进行 本篇文章配套的代码资源已经上传 点我下载源码 24、epoch循环训练------更新、评估、保存 这部分是训练过程的每个epoch结束之前执行的一…...
设计与实现)
基于51单片机的数字时钟(万年历)设计与实现
基于51单片机的数字时钟(万年历)设计与实现 摘要 随着科技的不断发展,数字时钟已成为人们日常生活中不可或缺的一部分。基于51单片机的数字时钟(万年历)设计,结合了传统时钟的功能与现代电子技术…...
2024年谷歌SEO的趋势预测及应对建议(川圣SEO)蜘蛛池
baidu搜索:如何联系八爪鱼SEO? baidu搜索:如何联系八爪鱼SEO? baidu搜索:如何联系八爪鱼SEO? 虽然说“SEO”已死这个口号已经喊了很多年了(最终也没死),但是在2023年很…...

Rust 生命周期符号使用的方法和规律
一、生命周期符号使用的规律 在 Rust 中,生命周期(lifetimes)是用于处理引用和所有权问题的关键概念。生命周期符号(通常表示为 a、b 等)用于指定引用的有效时间范围。这有助于编译器确保在引用被使用时,所…...
C卷(JavaPythonC++Node.jsC语言))
生成哈夫曼树(100%用例)C卷(JavaPythonC++Node.jsC语言)
给定长度为n的无序的数字数组,每个数字代表二叉树的叶子节点的权值,数字数组的值均大于等于1。请完成一个函数,根据输入的数字数组,生成哈夫曼树,并将哈夫曼树按照中序遍历输出。 为了保证输出的二又树中序遍历结果统一,增加以下限制:二叉树节点中,左节点权值小于等于右…...

el-form-item内的el-select如何自适应宽度
最近在使用element-ui做后台管理的时候,有个需求是在弹窗组件里面,添加一个el-select下拉框选项,但是给el-select设置的宽度无法自适应,原因很简单,我们不需要设置固定宽度,设置百分比就行了,让…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
