343. 整数拆分
343. 整数拆分
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
提示:
- 2 <= n <= 58
思路:(动态规划)
法一:
对于正整数 n,当 n ≥ 2 时,可以拆分成至少两个正整数的和。令 x 是拆分出的第一个正整数,则剩下的部分是 n − x,n − x 可以不继续拆分,或者继续拆分成至少两个正整数的和。由于每个正整数对应的最大乘积取决于比它小的正整数对应的最大乘积,因此可以使用动态规划求解。
创建数组 dp,其中 dp[i] 表示将正整数 i 拆分成至少两个正整数的和之后,这些正整数的最大乘积。特别地,0 不是正整数,1 是最小的正整数,0 和 1 都不能拆分,因此 dp[0] = dp[1] = 0。
当 i ≥ 2 时,假设对正整数 i 拆分出的第一个正整数是 j(1 ≤ j < i),则有以下两种方案:
- 将 i 拆分成 j 和 i − j 的和,且 i − j 不再拆分成多个正整数,此时的乘积是 j × (i − j);
- 将 i 拆分成 j 和 i − j 的和,且 i − j 继续拆分成多个正整数,此时的乘积是 j × dp[i − j]。
因此,当 j 固定时,有 dp[i] = max(j × (i − j), j × dp[i − j])。由于 j 的取值范围是 1 到 i − 1,需要遍历所有的 jjj 得到 dp[i] 的最大值,因此可以得到状态转移方程如下:
dp[i]=max1≤j<i{max(j×(i−j),j×dp[i−j])}d p[i]=\max _{1 \leq j<i}\{\max (j \times(i-j), j \times d p[i-j])\} dp[i]=1≤j<imax{max(j×(i−j),j×dp[i−j])}
最终得到 dp[n] 的值即为将正整数 n 拆分成至少两个正整数的和之后,这些正整数的最大乘积。
法二:
由于分解成正整数的乘积最大,若分解的正整数有1,不会使乘积变大,所以分解的正整数大于等于2;
- 又至少分解2个正整数,当 n = 2,或 n = 3 时,最大的乘积分别为1和2;
- n > 4 时,分解的最小整数为2,否则只会变小;
举一些栗子:
4 = 2 + 2 , 2 * 2 = 4
5 = 2 + 3, 2 * 3 = 6
6 = 3 + 3 , 3 * 3 = 9
7 = 2 + 2 + 3 = 2 + 5
8 = 2 + 3 + 3 = 2 + 6
9 = 4 + 2 + 3 = 2 + 7
10 = 3 + 3 + 4 = 3 + 7
- 创建数组 dp,其中 dp[i] 表示将正整数 i 拆分成至少两个正整数的和之后,这些正整数的最大乘积。
- 由以上可知分解的都可表示为 2 或 3 与另一个数 j,最大乘积就是2 或 3 乘以另一个数的最大乘积dp[j].
代码:(Java)
法一:
public class IntegerBreak {public static void main(String[] args) {// TODO Auto-generated method stubint n = 10;System.out.println(integerBreak(n));}int[] dp = new int[n + 1];dp[1] = 1;for (int i = 2; i <= n; i++) {for (int j = 1; j <= i - 1; j++) {dp[i] = Math.max(dp[i], Math.max(j * dp[i - j], j * (i - j)));}}return dp[n];
}
法二:
public class IntegerBreak {public static void main(String[] args) {// TODO Auto-generated method stubint n = 10;System.out.println(integerBreak(n));}public static int integerBreak(int n) {if(n / 2 < 2) {return n - 1;}int[] dp = new int[n + 1];dp[2] = 2;dp[3] = 3;for(int i = 4; i <= n; i++) {dp[i] = Math.max(2*dp[i-2], 3*dp[i-3]);}return dp[n];}
}
运行结果:
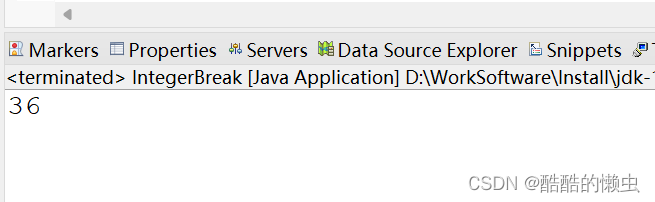
复杂度分析:
时间复杂度:O(n2)O(n^2)O(n2),其中 n 是给定的正整数。对于从 2 到 n 的每一个整数都要计算对应的 dp 值,计算一个整数对应的 dp 值需要 O(n) 的时间复杂度,因此总时间复杂度是 O(n2)。(法二时间复杂度为:O(n))
空间复杂度:O(n),其中 n 是给定的正整数。创建一个数组 dp,其长度为 n+1
注:仅供学习参考!
题目来源:力扣。
相关文章:

343. 整数拆分
343. 整数拆分 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k > 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n 2 输出: 1 解释: 2 1 1, 1 1 1。示例 2: 输入: n 10 输出: 36…...
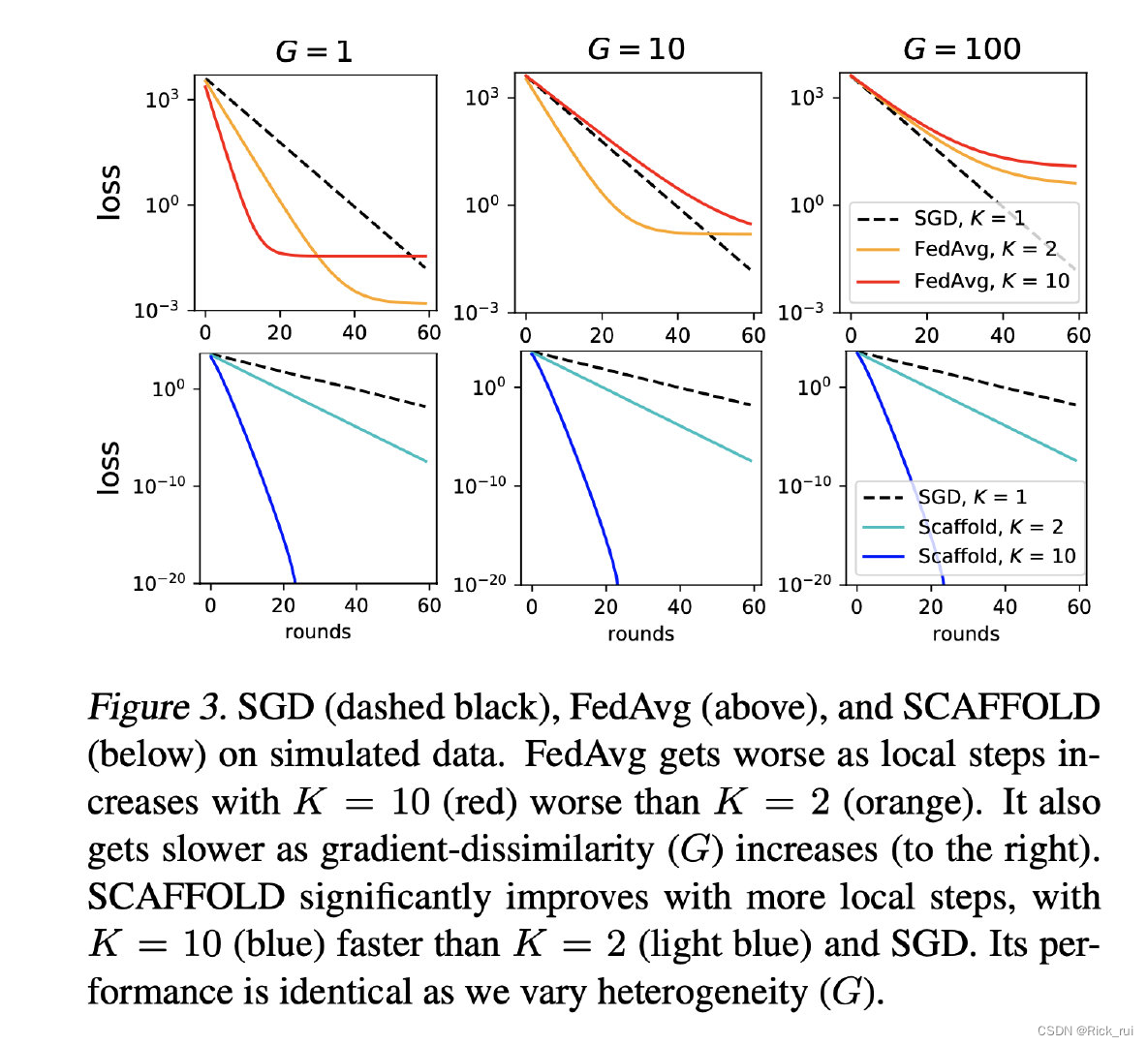
SCAFFOLD: Stochastic Controlled Averaging for Federated Learning学习
SCAFFOLD: Stochastic Controlled Averaging for Federated Learning学习背景贡献论文思想算法局部更新方式全局更新方式实验总结背景 传统的联邦学习在数据异构(non-iid)的场景中很容易产生“客户漂移”(client-drift )的现象,这会导致系统的收敛不稳定或者缓慢。…...
第十四届蓝桥杯三月真题刷题训练——第 3 天
目录 题目1:门牌制作 题目描述 运行限制 代码: 题目2:货物摆放_long 题目描述 答案提交 运行限制 代码: 题目3:跳跃_dp 题目描述 输入描述 输出描述 输入输出样例 运行限制 代码: 题目4&a…...

变量的四大存储类型static extern auto register
变量的四大存储类型static extern auto register外部变量(全局变量)extern----全局静态存储区定义 引用性声明❗易错点:函数之外未定义的变量一般是外部变量 extern全局变量 与 局部变量的区别‼️ 谨记:声明可以多次,…...

JavaScript基础五、语句
零、文章目录 文章地址 个人博客-CSDN地址:https://blog.csdn.net/liyou123456789个人博客-GiteePages:https://bluecusliyou.gitee.io/techlearn 代码仓库地址 Gitee:https://gitee.com/bluecusliyou/TechLearnGithub:https:…...

青龙面板399乐园
1.拉库 ql raw https://wjkjy.cn/wp-content/uploads/2023/03/1678104978-afaecb98a9df61e.js 2.抓包 7.26 399乐园 每天 七八毛左右 脚本已完成全部任务,自动提现 下载链接:https://3mao.lanzoul.com/izGDh084oogh 抓包链接 https://339.mhhuanyue.c…...

自动化注册组件
// components/index.js export default { install(app) { const req require.context(‘./’, false, /.vue$/) // console.log(req, ‘req’) req.keys().forEach((item) > { // console.log(item, ‘item’) const com req(item).default // console.log(com, ‘com’)…...

【JS代码优化一】分支优化篇
序:如何让代码看起来更优雅?代码是由文字堆叠起来的可以被机器执行的程序。它记载着相关信息(状态)、表达相关的情绪(函数),所以如何能够写出简洁、优雅、健壮、可维护性强的程序至关重要。本系…...

软件测试-接口测试-补充
文章目录 1.持续集成2. mock测试3.Fiddler 抓包工具3.1 弱网测试4. webservice1.持续集成 持续集成概念 重复执行开发提交代码并集成到主干; aim 加速产品迭代 好处 快速发现问题 避免分支大幅度偏离主干 加速产品发布 工具 git:源代码版本工具github:代码仓库jenkins:持续…...
:Beans自动装配)
Spring笔记(5):Beans自动装配
为什么需要使用自动装配 在通过XML配置文件进行设置Bean元素注入与声明注册后,我们能够发现一个问题,在项目中是会存在大量对象的,不可能全部都写在XML文件中,那会显得非常的臃肿,不利于后期维护,所以需要用…...

Spark+Vue+Springboot 协同过滤额音乐推荐大数据深度学习项目
一、项目背景 随着互联网的发展,大数据的到来,传统的音乐行业受到了很大的冲击,原有的音乐数字化给人们生活带来了极大的便利。随着数字音乐的兴起,各大音乐平台层出不穷,人们在音乐平台上收听音乐的时,常常因为歌曲信息繁杂,而不能找到自己想听的音乐。为了解决这个问题,音乐…...
JDBC的实现(IDEA版)
前期准备 开发环境: IDEA 2021.1.3 JAVA 1.8 MYSQL 8.0.32 msql用户名:root 密码:123 下载MySQL JDBC 驱动 前往MySQL官网下载对应版本的MySQL Connector/J驱动 (下载地址:https://dev.mysql.com/downloads/connector/j/ÿ…...
人员摔倒识别预警系统 人员跌倒检测算法 yolov7
人员摔倒识别预警系统 人员跌倒检测算法基于yolov7网络模型计算机识别技术,人员摔倒识别预警系统 人员跌倒检测算法对画面中人员摔倒进行实时检测识别抓拍告警。YOLOv7 的策略是使用组卷积来扩展计算块的通道和基数。研究者将对计算层的所有计算块应用相同的组参数和…...
Spring-Cloud-Gateway集成Nacos如何做负载均衡?
spring-cloud-alibaba的低版本 如果所用的SpringCloud和Nacos的版本信息如下: <spring-cloud.version>Hoxton.SR10</spring-cloud.version> <spring-cloud-alibaba.version>2.2.6.RELEASE</spring-cloud-alibaba.version>网关的依赖如下&…...

【数据挖掘与商务智能决策】第四章 逻辑回归模型
逻辑回归模型算法原理 逻辑回归模型的数学原理 %matplotlib inline# 补充知识点:Sigmoid函数绘制 import matplotlib.pyplot as plt import numpy as npx = np.linspace(-6, 6) # 通过linspace()函数生成-6到6的等差数列,默认50个数 y = 1.0...

滚动升级回滚
滚动升级回滚 ReplicationController 资源文件 apiVersion: v1 kind: ReplicationController metadata:name: kubia-v1labels:app: kubia spec:replicas: 3template:metadata:name: kubialabels:app: kubiaspec:containers:- image: luksa/kubia:v1name: nodejes --- apiVer…...
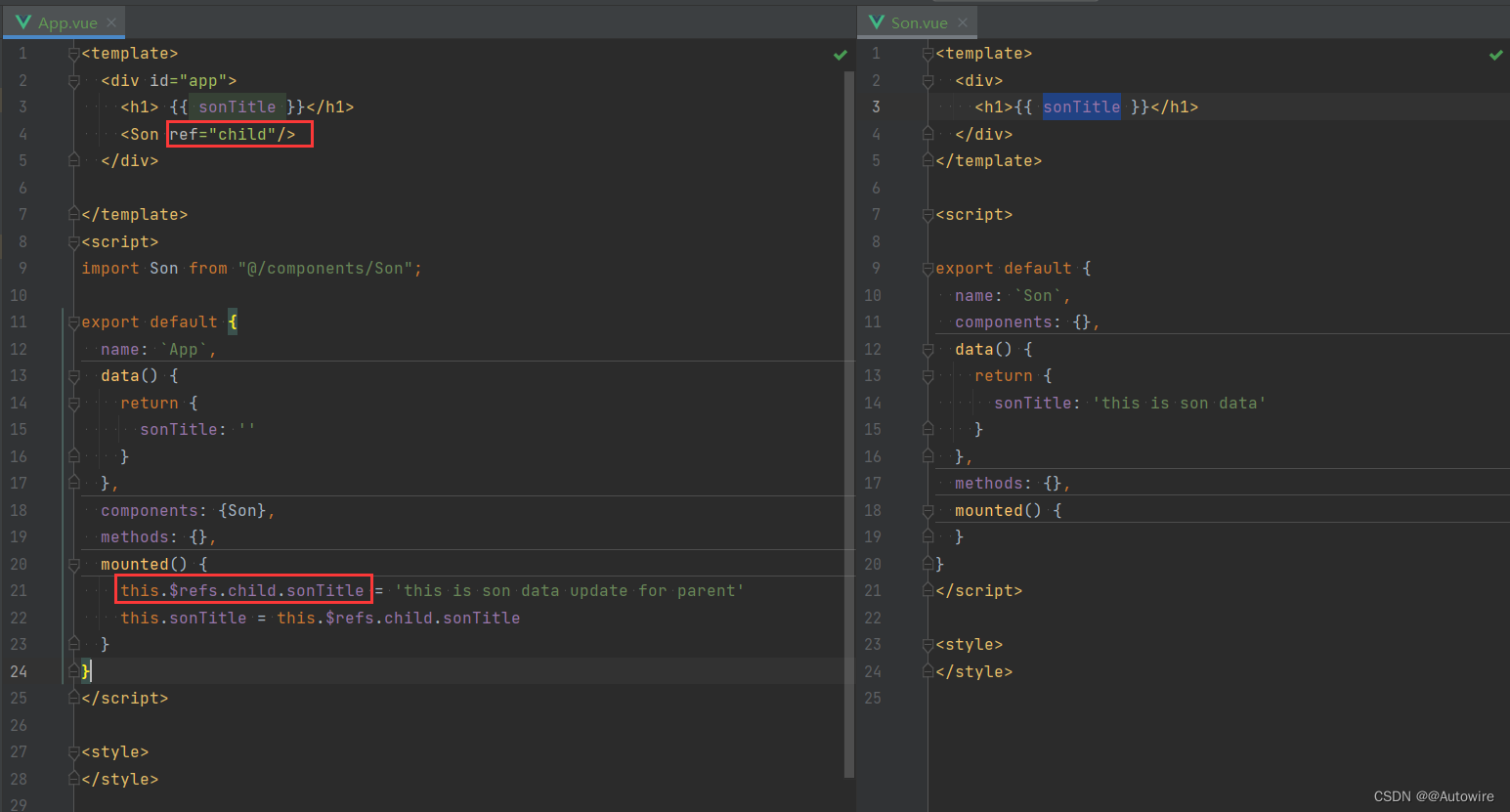
2023/3/6 VUE - 组件传值【通信】方式
1 父亲传子代传值【子代使用父代的数据】 1.1 props传值 父亲给儿子传值: 爷爷给孙子传值: 这个props传值的方式,只能一代一代的往下传,不能跨代传值。 有一个问题:子组件不能修改父组件的值: 1.2 …...
MedCalc v20.217 医学ROC曲线统计分析参考软件
MedCalc是一款医学 ROC 曲线统计软件,用于ROC曲线分析的参考软件,医学工作者设计的医学计算器,功能齐全。它可以帮助医生快速作出普通的医学计算,从而对症下药。提供超过76种常用的规则和方法,包括:病人数据、单位参数、费用计算等等。甚至可以将图形另存为BMP,PNG,GIF…...

欢乐消除开心假日协议解密
欢乐消除开心假日协议解密协/议/流/量/解/密分析欢乐消除开心假日这款游戏流量的协议加密方式。序欢乐消除开心假日是一款合成模拟家装的游戏,在这个游戏中,你将成为一位充满热情的设计师,与好友一起经营工作室。你需要根据客户的需求重新设计…...
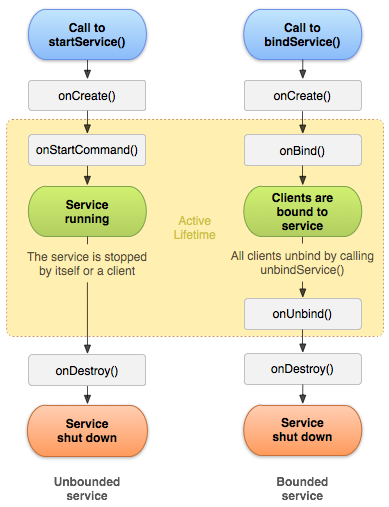
Android Service知识
一. 概览 Service 是一种可在后台执行长时间运行操作而不提供界面的应用组件。服务可由其他应用组件启动,而且即使用户切换到其他应用,服务仍将在后台继续运行。此外,组件可通过绑定到服务与之进行交互,甚至是执行进程间通信 (IPC…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...
