蓝桥杯C++大学B组一个月冲刺记录2024/3/13
蓝桥杯C++大学B组一个月冲刺记录2024/3/13
规则:每日三题
向日葵的花语是说不出的爱恋
不过今天有点水题了
1.有序分数
给定一个整数 N,请你求出所有分母小于或等于 N,大小在 [0,1] 范围内的最简分数,并按从小到大顺序依次输出。
这个题在被划分为递归一章,是由于Stern-Brocot Tree可以通过中序递归来解决这个问题
但是这个题数据范围仅n <160。所以时间复杂度为O(n2logn)的暴力做法也可以解决这个题
#include<iostream>
#include<vector>
#include<algorithm>using namespace std;typedef pair<int,int>PII;vector<PII>q;int n;bool cmp(PII a,PII b){return a.first * b.second < a.second * b.first;
}int gcd(int a,int b){return b?gcd(b,a % b):a;
}int main(){cin >> n;q.push_back({0,1});for(int i = 1;i <= n; ++i){for(int j = 1;j <= i;++j){if(gcd(i,j) == 1) q.push_back({j,i});} }sort(q.begin(),q.end(),cmp);for(int i = 0;i < q.size();++i){cout << q[i].first << '/' << q[i].second << endl;}return 0;
}
以下是y总的递归做法,时间复杂度O(n2)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;int n;void dfs(int a, int b, int c, int d)
{if (a + c > n) return;dfs(a, b, a + c, b + d);printf("%d/%d\n", b + d, a + c);dfs(a + c, b + d, c, d);
}int main()
{scanf("%d", &n);puts("0/1");dfs(1, 0, 1, 1);puts("1/1");return 0;
}
2.递归实现指数型枚举
从 1∼n这 n个整数中随机选取任意多个,输出所有可能的选择方案。
简单的dfs,比较巧妙的是用二进制编码来记录状态
#include<iostream>using namespace std;const int M = 20;int p[M];
int n;void dfs(int i){if(i > n){for(int i = 1;i <= n; ++i){if(p[i] == 1) cout << i << ' ';else continue; }cout << '\n';}else{p[i] = 1;dfs(i + 1);p[i] = 0;dfs(i + 1);}}int main(){cin >> n;dfs(1);return 0;
}
相关文章:

蓝桥杯C++大学B组一个月冲刺记录2024/3/13
蓝桥杯C大学B组一个月冲刺记录2024/3/13 规则:每日三题 向日葵的花语是说不出的爱恋 不过今天有点水题了 1.有序分数 给定一个整数 N,请你求出所有分母小于或等于 N,大小在 [0,1] 范围内的最简分数,并按从小到大顺序依次输出。 这个题在被划…...

计算机网络——Internet结构和ISP
互联网结构:网络的网络 ISP:互联网服务提供商(Internet Service Provider,ISP)是指为用户提供互联网接入服务的组织或公司。ISP在互联网结构中扮演着关键的角色,它们通过建立网络基础设施和提供网络连接服…...

E.接龙数列【蓝桥杯】/动态规划
接龙数列 题目描述 对于一个长度为 K 的整数数列:A1, A2, . . . , AK,我们称之为接龙数列当且仅当 Ai 的首位数字恰好等于 Ai−1 的末位数字 (2 ≤ i ≤ K)。 例如 12, 23, 35, 56, 61, 11 是接龙数列;12, 23, 34, 56 不是接龙数列…...
将二维转化为彩色图像)
cv2.cvtColor()将二维转化为彩色图像
我们如果要将一维的图像转化为三维的彩色图像 import cv2 img cv2.cvtColor(img.squeeze(0), cv2.COLOR_GRAY2BGR) 这里的img.squeeze为二维数据,img为三维数据,所以压缩掉一个维度 。这样就将图像转化为了三维彩色图像。 cv2.imshow(Image, img) c…...
为什么 VSCode 不用 Qt 而要用 Electron?
为什么 VSCode 不用 Qt 而要用 Electron? 在开始前我有一些资料,是我根据网友给的问题精心整理了一份「Qt 的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!&am…...
环信ChatroomUIKit功能详解——超详细介绍
聊天室是当下泛娱乐社交应用中最经典的玩法,通过调用环信的 IM SDK 接口,可以快速创建聊天室。如果想根据自己业务需求对聊天室应用的 UI界面、弹幕消息、礼物打赏系统等进行自定义设计,最高效的方式则是使用环信的 ChatroomUIKit 。 文档地址…...
)
怎么读取springboot中的properties.yml配置文件里的配置值(亲测有效)
怎么读取springboot中的properties.yml配置文件里的配置值 test:username: name主配置类中加上 EnableConfigurationProperties(MailConfigProperties.class)类上加ConfigurationPropetise("test“),属性就会自动注入配置值; ConfigurationPropetise("…...
18、设计模式之解释器模式(Interpreter)
一、什么是解释器模式 解释器模式是一种行为型设计模式。解释器模式就像是一种自定义语言,我们可以定义该语言的语法规则,然后从中解析出具体的命令或表达式,最终执行相应的操作。 eg:这种模式比较冷门,不怎么使用。 …...

cpp qt 一个奇怪的bug
今天在用cpp qt的时候发现了一个奇怪的东西 这是我的源代码 #include "mywidget.h" #include <QPushButton>myWidget::myWidget(QWidget *parent): QWidget(parent) {QPushButton * btn1 new QPushButton;btn1->show();btn1->setParent(this);btn1-&g…...
)
第6章:MATLAB文本数据处理进阶篇的目录 (MATLAB入门课程)
讲解视频:可以在bilibili搜索《MATLAB教程新手入门篇——数学建模清风主讲》。 MATLAB教程新手入门篇(数学建模清风主讲,适合零基础同学观看)_哔哩哔哩_bilibili 第6章:MATLAB文本数据处理进阶篇 6.1 文本格式化 …...
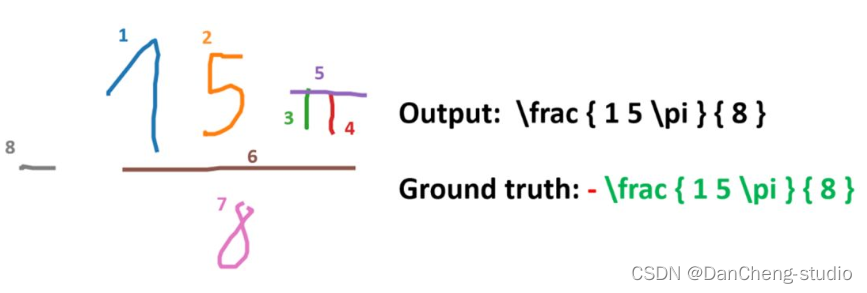
软件杯 深度学习 opencv python 公式识别(图像识别 机器视觉)
文章目录 0 前言1 课题说明2 效果展示3 具体实现4 关键代码实现5 算法综合效果6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于深度学习的数学公式识别算法实现 该项目较为新颖,适合作为竞赛课题方向,学…...
vscode通过多个跳板机连接目标机(两种方案亲测成功)
1、ProxyJump(推荐使用) 需要OpenSSH 7.3以上版本才可使用,可用下列命令查看: ssh -V ProxyJump命令行使用方法 ssh -J [email protected]:port1,[email protected]:port2 一层跳板机: ssh dst_usernamedst_ip -…...

C++基础复习003
vector去重 第一种,利用set容器的特性进行去重: #include <iostream> #include <vector> #include <set> using namespace std; int main() {vector<int>test{1,2,3,3,3,4,2,3,5,2,63,56,34,24};set<int>s(test.begin(),…...

Docker Commit提交
Docker Commit提交 Docker Commit镜像提交 以一个正在运行的tomcat为例因为docker拉取的镜像都是删减版,所以需要将webapp.dist的文件内容复制到webapps中再将自己制作的镜像放在正在运行服务器上,不是云端服务器上 #进入tomcat,这是一个正…...

百度现在应该怎么去做搜索SEO优化?(川圣SEO)蜘蛛池
baidu搜索:如何联系八爪鱼SEO? baidu搜索:如何联系八爪鱼SEO? baidu搜索:如何联系八爪鱼SEO? 百度搜索引擎优化(SEO)是一种通过优化网站,提升网页在百度搜索结果中的排…...

登录凭证------
为什么需要登录凭证? web开发中,我们使用的协议http是无状态协议,http每次请求都是一个单独的请求,和之前的请求没有关系,服务器就不知道上一步你做了什么操作,我们需要一个办法证明我没登录过 制作登录凭…...
matplotlib系统学习记录
日期:2024.03.12 内容:将matplotlib的常用方法做一个记录,方便后续查找。 基本使用 # demo01 from matplotlib import pyplot as plt # 设置图片大小,也就是画布大小 fig plt.figure(figsize(20,8),dpi80)#图片大小,清晰度# 准…...

【DL】ML系统学习笔记 1
【DL】ML系统学习笔记 1 1. 机器学习定义2. 机器学习三大任务3. 机器学习定义回归举例4. Gradient Descent 优化5. Gradient Descent 优化步骤6. 回归步骤小姐7. Linear models8. 核心步骤流程9. 模型优化9. 深度学习引出1. 机器学习定义 Machine Learning Looking for Functio…...

ffmpeg视频处理常用命令
1.ffmpeg主要参数 -f fmt(输入/输出) 强制输入或输出文件格式。 格式通常是自动检测输入文件, 并从输出文件的文件扩展名中猜测出来,所以在大多数情况下这个选项是不需要的。-i url(输入) 输入文件的网址-…...

前端npm和yarn更换国内淘宝镜像
NPM 查询当前镜像 npm get registry 设置为淘宝镜像 npm config set registry https://registry.npm.taobao.org/ (旧地址) npm config set registry https://registry.npmmirror.com/ (最新地址) 设置为官方镜像 npm config set registry https://registry.n…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
