C# 对于点位置的判断
1.判断点是否在一群点内部
要判断一个点是否在一个由多个点围成的多边形内部(例如一圈点),可以使用射线法(Ray Casting Algorithm)来实现。以下是一个简单的 C# 实现示例
using System;public class Point
{public double X { get; set; }public double Y { get; set; }public Point(double x, double y){X = x;Y = y;}
}public class Program
{public static bool IsPointInPolygon(Point testPoint, Point[] polygon){bool inside = false;int count = polygon.Length;for (int i = 0, j = count - 1; i < count; j = i++){if (((polygon[i].Y > testPoint.Y) != (polygon[j].Y > testPoint.Y)) &&(testPoint.X < (polygon[j].X - polygon[i].X) * (testPoint.Y - polygon[i].Y) / (polygon[j].Y - polygon[i].Y) + polygon[i].X)){inside = !inside;}}return inside;}public static void Main(){Point[] polygon = new Point[]{new Point(0, 0),new Point(0, 4),new Point(4, 4),new Point(4, 0)};Point testPoint = new Point(2, 2);bool isInside = IsPointInPolygon(testPoint, polygon);Console.WriteLine($"Point ({testPoint.X}, {testPoint.Y}) is inside the polygon: {isInside}");}
}
2.判断点在直线左侧还是右侧
要在C#中判断一个点在一条直线的左侧还是右侧,可以使用点与直线方程的方法。具体来说,对于直线上的两个点A和B,以及要测试的点P,可以通过计算点P相对于直线AB的位置来确定其是否在直线的左侧还是右侧。
以下是一个简单的C#示例:
using System;public class Point
{public double X { get; set; }public double Y { get; set; }public Point(double x, double y){X = x;Y = y;}
}public class Line
{public Point A { get; set; }public Point B { get; set; }public Line(Point a, Point b){A = a;B = b;}// 计算点P相对于直线AB的位置public double PointRelativeToLine(Point P){return (B.X - A.X) * (P.Y - A.Y) - (B.Y - A.Y) * (P.X - A.X);}
}public class Program
{public static void Main(){Point pointA = new Point(1, 1);Point pointB = new Point(4, 5);Line lineAB = new Line(pointA, pointB);Point testPoint = new Point(2, 3);double position = lineAB.PointRelativeToLine(testPoint);if (position > 0){Console.WriteLine("Point is on the left side of the line.");}else if (position < 0){Console.WriteLine("Point is on the right side of the line.");}else{Console.WriteLine("Point is on the line.");}}
}3.判断两条直线的交点
要判断两条直线的交点,可以使用直线的参数方程来求解。两条直线的参数方程可以表示为:
直线1: (x = x_1 + t_1 \cdot (x_2 - x_1)) 和 (y = y_1 + t_1 \cdot (y_2 - y_1))
直线2: (x = x_3 + t_2 \cdot (x_4 - x_3)) 和 (y = y_3 + t_2 \cdot (y_4 - y_3))
要求两条直线的交点,需要解方程组,即求解 (t_1) 和 (t_2),然后代入其中一个直线的参数方程中即可求得交点的坐标。
以下是一个C#示例:
using System;public class Point
{public double X { get; set; }public double Y { get; set; }public Point(double x, double y){X = x;Y = y;}
}public class Line
{public Point A { get; set; }public Point B { get; set; }public Line(Point a, Point b){A = a;B = b;}// 计算两条直线的交点public Point IntersectionPoint(Line otherLine){double x1 = A.X;double y1 = A.Y;double x2 = B.X;double y2 = B.Y;double x3 = otherLine.A.X;double y3 = otherLine.A.Y;double x4 = otherLine.B.X;double y4 = otherLine.B.Y;double denominator = (x1 - x2) * (y3 - y4) - (y1 - y2) * (x3 - x4);if (denominator == 0){throw new InvalidOperationException("Lines are parallel. No intersection point exists.");}double t1 = ((x1 - x3) * (y3 - y4) - (y1 - y3) * (x3 - x4)) / denominator;double t2 = -((x1 - x2) * (y1 - y3) - (y1 - y2) * (x1 - x3)) / denominator;double intersectionX = x1 + t1 * (x2 - x1);double intersectionY = y1 + t1 * (y2 - y1);return new Point(intersectionX, intersectionY);}
}public class Program
{public static void Main(){Point pointA1 = new Point(1, 1);Point pointB1 = new Point(4, 5);Line line1 = new Line(pointA1, pointB1);Point pointA2 = new Point(2, 3);Point pointB2 = new Point(6, 1);Line line2 = new Line(pointA2, pointB2);try{Point intersectionPoint = line1.IntersectionPoint(line2);Console.WriteLine($"Intersection Point: ({intersectionPoint.X}, {intersectionPoint.Y})");}catch (InvalidOperationException ex){Console.WriteLine(ex.Message);}}
}相关文章:

C# 对于点位置的判断
1.判断点是否在一群点内部 要判断一个点是否在一个由多个点围成的多边形内部(例如一圈点),可以使用射线法(Ray Casting Algorithm)来实现。以下是一个简单的 C# 实现示例 using System;public class Point {public d…...
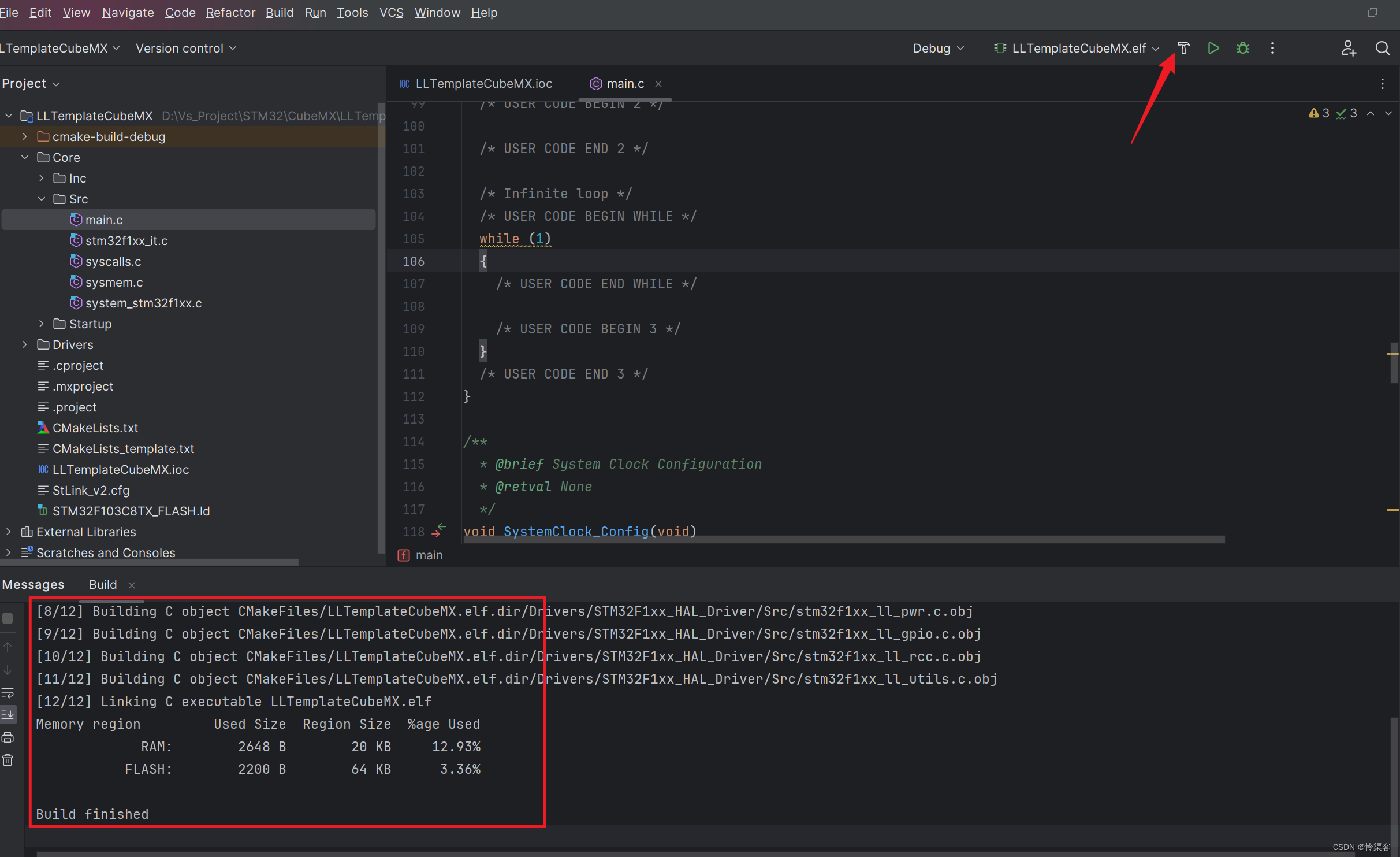
最新CLion + STM32 + CubeMX 开发环境搭建
网上有不少相关教程,但都是基于老版本Clion,新版有一些改变,但整体是简单了。 PS:本教程基于CLion 2023.3.4 安装所需工具参考:Clion搭建stm32开发环境(STM32F103C8T6),有这一篇就够…...

【Python3】观察者模式
观察者模式(Observer Pattern)是一种常见的设计模式,用于定义对象之间的一对多依赖关系,使得一个对象的状态改变能够通知所有依赖于它的对象并自动更新。 在观察者模式中,有两个核心角色: Subject…...
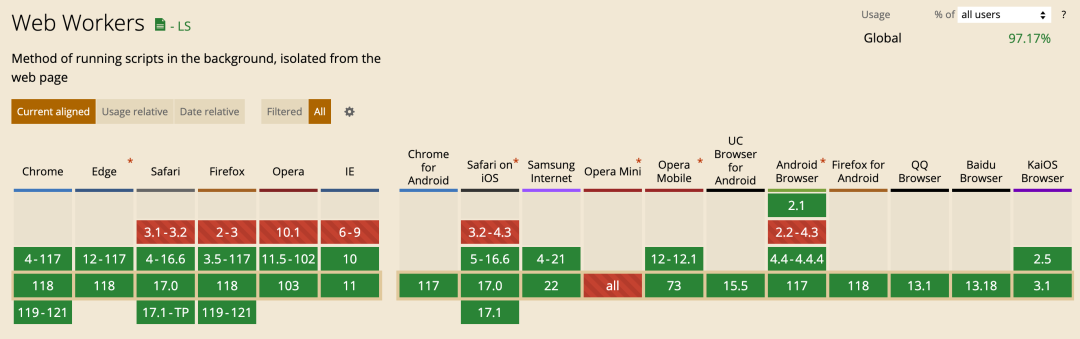
HTML5 Web Worker之性能优化
描述 由于 JavaScript 是单线程的,当执行比较耗时的任务时,就会阻塞主线程并导致页面无法响应,这就是 Web Workers 发挥作用的地方。它允许在一个单独的线程(称为工作线程)中执行耗时的任务。这使得 JavaScript 代码可…...

应对恶意IP攻击的有效方法
在当今数字化时代,网络攻击已经成为了互联网安全的重大挑战之一。恶意IP攻击是网络安全领域中的一种常见威胁,它可能导致数据泄露、服务中断、系统瘫痪等严重后果。因此,有效地应对恶意IP攻击至关重要。IP数据云将深入探讨如何应对恶意IP攻击…...
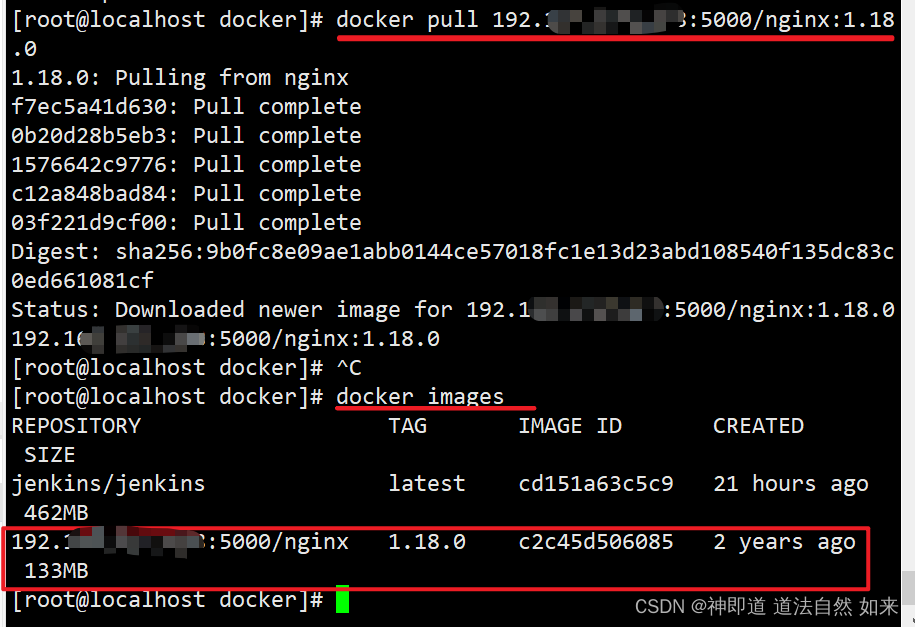
如何使用“Docker registry创建本地仓库,在服务器之间进行文件push和pull”?
1.1、在服务器1,运行registry docker run -d -p 5000:5000 -v ${PWD}/registry:/var/lib/registry --restart always --name registry registry:2.7.11.2、编辑/etc/docker/daemon.json 文件, 192.168.xxx.xxx 换成你自己 registry 服务的地址 sudo na…...
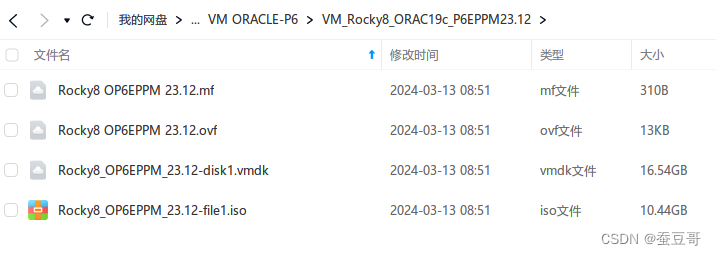
Rocky Linux - Primavera P6 EPPM 安装及分享
引言 继上一期发布的Redhat Linux版环境发布之后,近日我又制作了基于Rocky Enterprise Linux 的P6虚拟机环境,同样里面包含了全套P6 最新版应用服务 此虚拟机仅用于演示、培训和测试目的。如您在生产环境中使用此虚拟机,请先与Oracle Primav…...

API 管理调研
当前大部分团队内 API 管理都是依赖 Postman,postman最大的问题是共享问题,如果我要使用另外一个人已经调试好的 API 非常麻烦。因此,能实现协作的 API 管理将极大提升效率。 Yapi https://github.com/YMFE/yapi https://hellosean1025.gi…...
在centOS服务器安装docker,并使用docker配置nacos
遇到安装慢的情况可以优先选择阿里镜像 安装docker 更新yum版本 yum update安装所需软件包 yum install -y yum-utils device-mapper-persistent-data lvm2添加Docker仓库 yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.rep…...

JVM运行时数据区概述以及分别存放的内容
JVM的运行时数据区是JVM在执行Java程序时用于存储数据和状态信息的内存区域。它分为多个部分,每个部分都有其特定的作用和存放的内容。 1. 方法区(Method Area) 作用:方法区是所有线程共享的内存区域,用于存放已被虚…...

数据体系规范化
基础是标准化、规范化 建立数据仓库,面向主题的、集成的、相对稳定的、反映历史变化的数据集合,以支持管理决策decision making 大数据:大量volumn、多样variety、快速velocity、价值密度低value、准确性veracity、可视化visualization、合法性validity 多源数据、多样数…...

从政府工作报告探计算机行业发展
从政府工作报告中,我们可以深入洞察计算机行业在未来一年的发展趋势和政策导向。报告中明确提出了数字经济创新发展的重要性,以及制造业数字化转型、服务业数字化、智慧城市和数字乡村建设等关键任务,这些都为计算机行业提供了广阔的发展空间…...
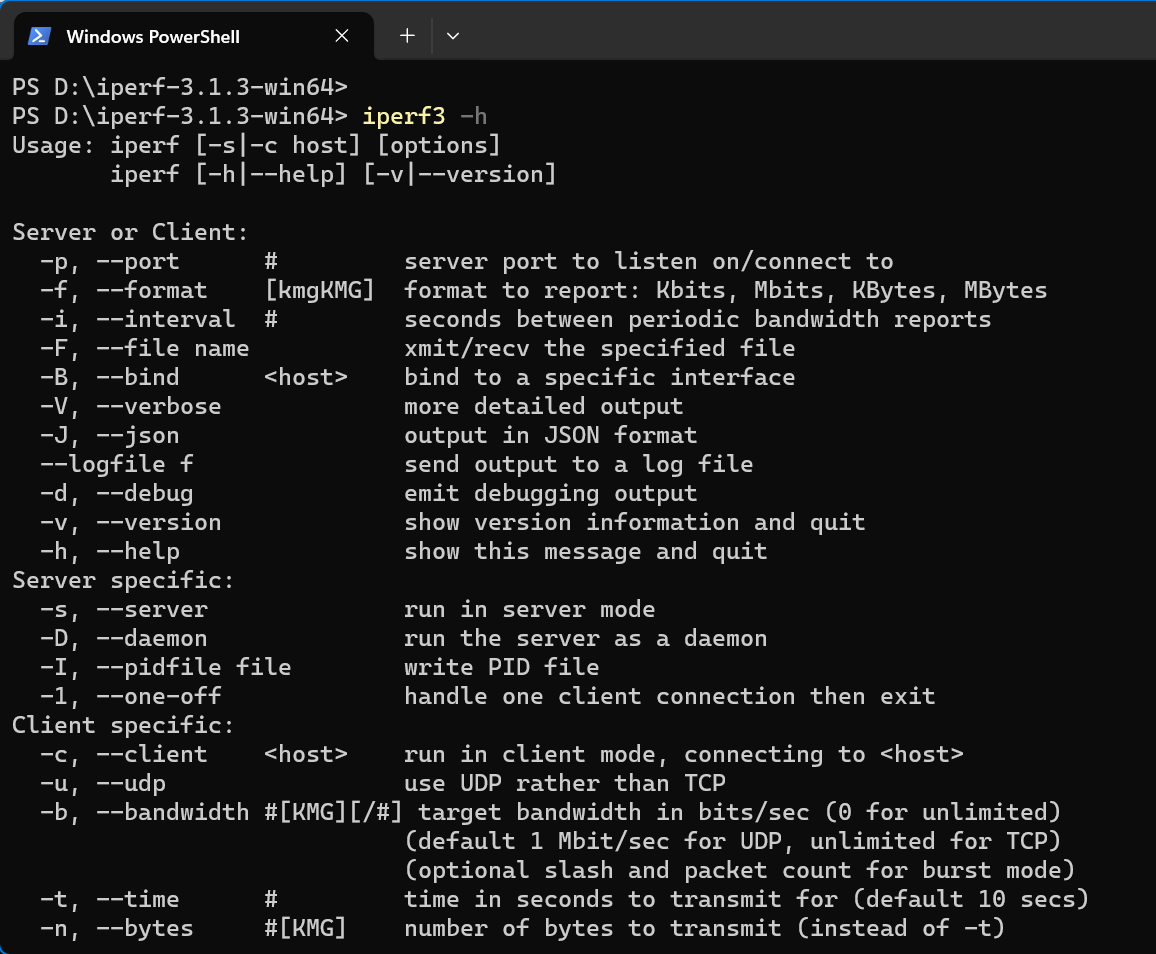
【软件工具】网络性能测试工具 Iperf
Iperf 是一款专业的开源网络性能测试工具,它被广泛用于测量网络带宽、延迟、抖动和数据包丢失等网络性能指标,支持 TCP 和 UDP 等,可用于点对点或客户端-服务器等模式的网络测试。 软件获取 官方下载地址:https://iperf.fr/iper…...
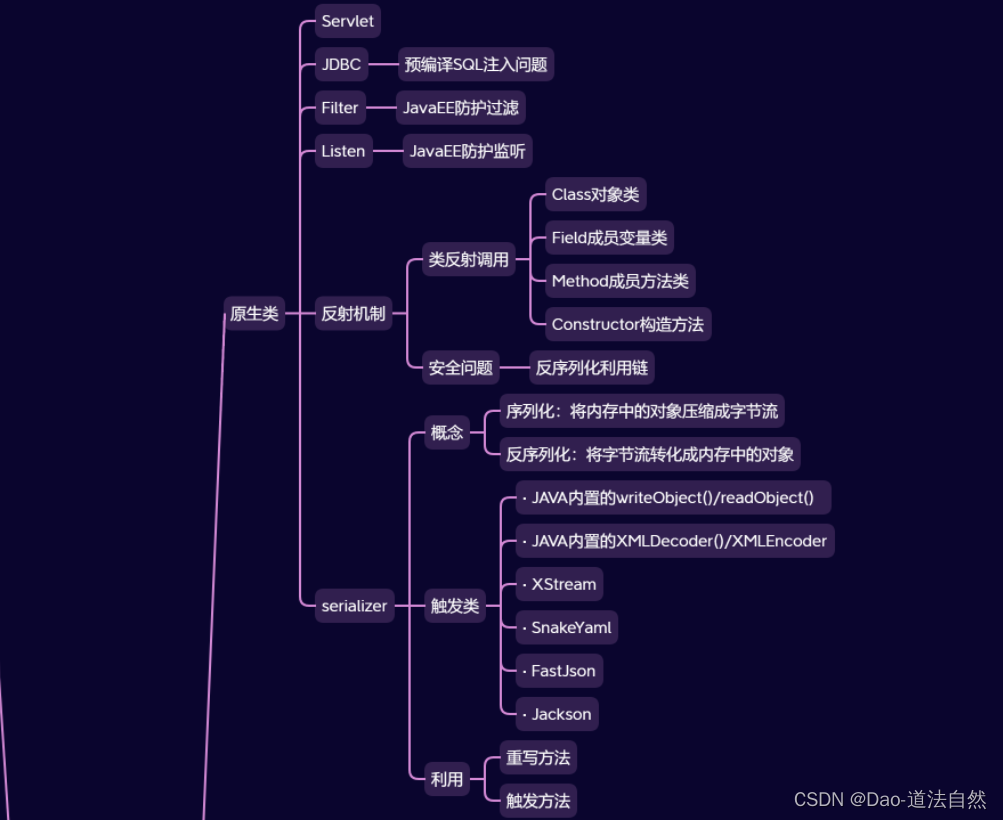
Day32:安全开发-JavaEE应用Servlet路由技术JDBCMybatis数据库生命周期
目录 JavaEE-HTTP-Servlet&路由&周期 JavaEE-数据库-JDBC&Mybatis&库 思维导图 Java知识点: 功能:数据库操作,文件操作,序列化数据,身份验证,框架开发,第三方库使用等. 框架…...

C语言下使用SQL语言
需头文件:#include<sqlite.h>---需下载 1.sqlite3_open int sqlite3_open( const char *filename, /* Database filename (UTF-8) */ sqlite3 **ppDb /* OUT: SQLite db handle */ ); 功能: 打开数据库文件(…...

Gitea相关漏洞
Go代码审计:Gitea远程命令执行漏洞链_新闻中心-网盾网络安全培训学校 Vulhub靶场gitea-1.4远程代码执行漏洞复现_gitea 漏洞-CSDN博客...
基于深度学习的图像去雨去雾
基于深度学习的图像去雨去雾 文末附有源码下载地址 b站视频地址: https://www.bilibili.com/video/BV1Jr421p7cT/ 基于深度学习的图像去雨去雾,使用的网络为unet, 网络代码: import torch import torch.nn as nn from torchsumm…...

使用JS的for循环实现九九乘法表
九九乘法表是我们在学习基础数学时经常会遇到的一个概念。在编程中,使用循环结构来实现九九乘法表是一个很好的练习。下面,我将详细介绍如何使用JavaScript的for循环来实现九九乘法表。 首先,我们需要理解for循环的基本结构。在JavaScript中…...
Leetcode 70 爬楼梯
文章目录 1. 题目描述2. 我的尝试 1. 题目描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 示例 1: 输入:n 2 输出:2 解释:有两种方法可以爬到…...
基于SpringBoot+MYSQL+Vue的校园管理系统
目录 1、前言介绍 2、主要技术 3、系统流程分析 3.1、操作流程 3.2、添加信息流程 3.3、删除信息流程 4、系统设计 4.1 系统体系结构 4.2开发流程设计 4.3 数据库设计原则 4.4 数据表 5、运行截图(部分) 5.1管理员功能模块 5.2用户功能模块 5.3院校管理员功能模块…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
