Leetcode 70 爬楼梯
文章目录
- 1. 题目描述
- 2. 我的尝试
1. 题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
2. 我的尝试
非常经典且基础的动态规划问题,状态转移方程为 d p [ i ] = d p [ i − 1 ] + d p [ i − 2 ] dp[i] = dp[i-1] + dp[i-2] dp[i]=dp[i−1]+dp[i−2]
class Solution {
public:int climbStairs(int n) {int f[n + 1];f[0] = f[1] = 1;for (int i = 2; i <= n; i++)f[i] = f[i - 1] + f[i - 2];return f[n];}
};
相关文章:

Leetcode 70 爬楼梯
文章目录 1. 题目描述2. 我的尝试 1. 题目描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 示例 1: 输入:n 2 输出:2 解释:有两种方法可以爬到…...
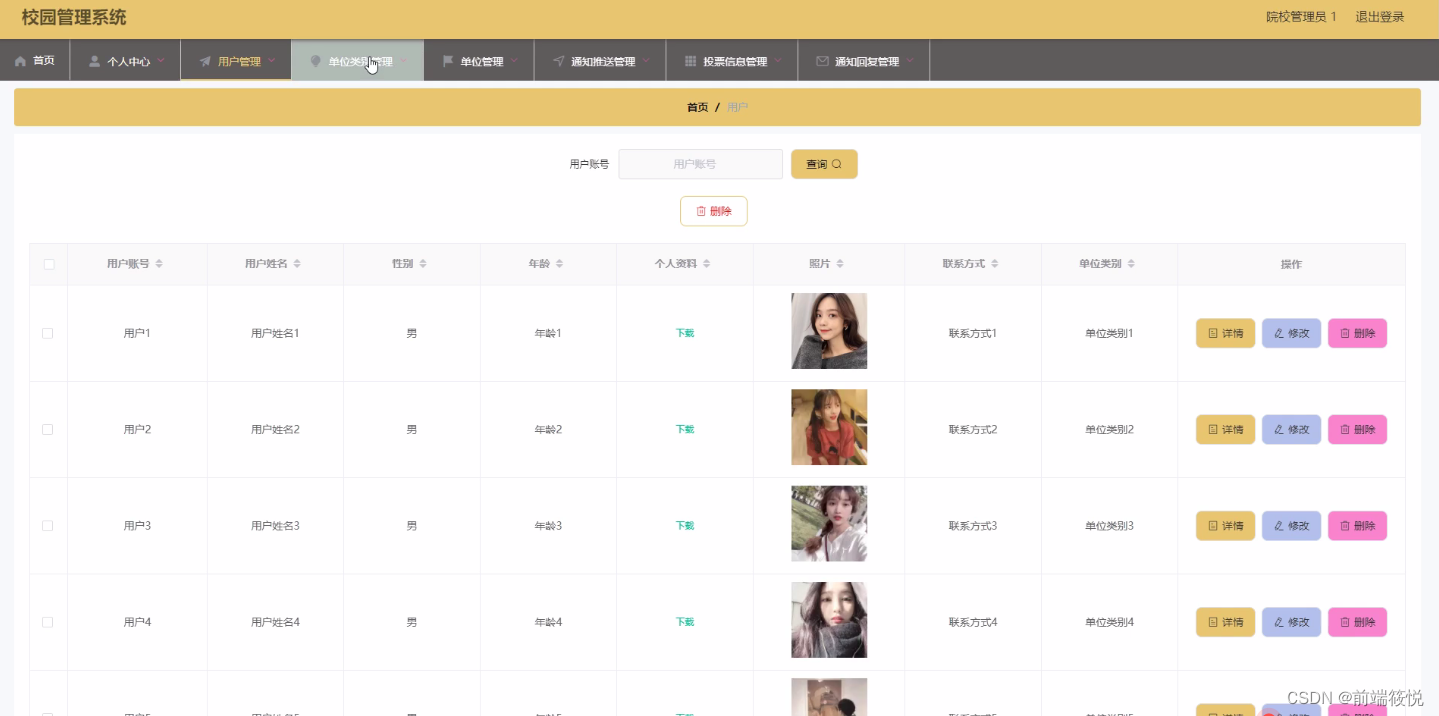
基于SpringBoot+MYSQL+Vue的校园管理系统
目录 1、前言介绍 2、主要技术 3、系统流程分析 3.1、操作流程 3.2、添加信息流程 3.3、删除信息流程 4、系统设计 4.1 系统体系结构 4.2开发流程设计 4.3 数据库设计原则 4.4 数据表 5、运行截图(部分) 5.1管理员功能模块 5.2用户功能模块 5.3院校管理员功能模块…...
Oracle P6 负浮时和必须完成日期
前言 学习过计划的人大都有这有这样的经历,即无论是Microsoft Project 亦或是P6见过负浮时那么 Primavera P6 计划中的负浮时是从何而来的呢,那么本文可能会有所帮助。 首先,当活动的最晚日期早于最早日期时,就会出现负浮时。 换…...

【C++】STL--String
这一节主要总结string类的常见接口,以及完成了string类的模拟实现。 目录 标准库的String类 string类常见接口 string类对象的常见构造 string析构函数:~string string类对象的容量操作 string类对象的访问及遍历操作 string类对象的修改操作 s…...

深入理解与使用go之中间件--实现
深入理解与使用go之--中间件实现 目录 引子 中间件 定义 原理 简单实现 多个中间件 优化 扩展 gin框架实现 引子 我们在做web开发的时候,经常会遇到下面一些需求: 统计耗时:想程序内部统计某个路由的请求耗时 预处理:接口需要登录鉴权后才能继续进行 错误捕获:当…...

移动端研发技术的进化历程
移动端研发技术 移动端研发技术主要分为原生开发和跨平台开发。本章主要介绍一下移动开发技术的过去、当下和未来,一步一步介绍移动技术的进化历程。 原生开发 原生应用程序是指某一个移动平台(比如iOS或Android)所特有的应用,使…...
ChromeDriver 122 版本为例 国内下载地址及安装教程
ChromeDriver 国内下载地址 https://chromedriver.com/download 靠谱 千千万万别下载错了 先确认 Chrome 浏览器版本 以 win64 版本为例 那我们下载这一个啊,不要下载错了 下载地址贴在这哈 https://storage.googleapis.com/chrome-for-testing-public/122.0.…...

【数据结构】双向链表及LRU缓存的实现
目录 前言 1. 在原有的自定义链表类 Linked 的基础上,添加新的 “节点添加”方法 addNode(Node node) 测试用例 测试结果 2. 在自定义链表类的基础上,使用双重循环“强力” 判断两个节点是否发生相交 测试用例 测试结果 3. 在自定义链表类的基础上…...

2、计划任务不显示UI的问题
计划任务不显示UI的问题 1、原因: 在windows7以上系统,使用system权限启动的进程默认是没有ui界面,这是windows系统出于安全考虑的限制。防止用户在高权限下误删重要的文件。 2、解决方案: 1、降权 解决的办法:降…...

学C还是学C++?
计算机专业学生,大一上学期学习了C语言,下学期学校要学C,请问我寒假继续深入学习C还是提前学C,大佬们有什么建议吗?(个人感觉C学的不是很明白,链表文件什么的还不是很懂…) 这个并没有一个统一的…...

Springboot参数分组校验
Springboot参数分组校验 文章目录 Springboot参数分组校验简介代码准备单个或多个参数的校验非 JSON 格式的对象参数校验JSON 格式的对象参数校验Service 层校验项目地址 简介 Java API规范(JSR303)定义了Bean校验的标准validation-api,但没有提供实现。hibernate …...

无缝集成 MongoDB Relational Migrator,Tapdata 提供关系型到 MongoDB 实时迁移优化方案
在去年的 MongoDB 用户大会纽约站上,MongoDB 正式宣布全面推出新工具 MongoDB Relational Migrator(MongoDB RM),用以简化应用程序迁移和转换——即从传统关系型数据模型到现代的文档数据模型,助力组织快速提升运营效率…...

【C++】每日一题 146 LRU缓存
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。 实现 LRUCache 类: LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存 int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 …...

CentOS搭建NAS服务器并使用
CentOS搭建NAS服务器并使用 文章目录 前言一、配置NAS服务器安装 NFS 服务:启动 NFS 服务:使 NFS 服务在系统启动时自动启动: 二、挂载服务器三、常见错误以及解决方案1、mount.nfs: No route to host2、mount.nfs: access denied by server …...
爬虫入门到精通_框架篇16(Scrapy框架基本使用)_名人名言的抓取
1 目标站点分析 抓取网站:http://quotes.toscrape.com/ 主要显示了一些名人名言,以及作者、标签等等信息: 点击next,page变为2: 2 流程框架 抓取第一页:请求第一页的URL并得到源代码,进行下…...
)
mac inter 芯片遇到程序无法打开(无法验证开发者)
mac inter 芯片遇到程序无法打开(无法验证开发者) 解决方案 终端运行命令: sudo xattr -r -d com.apple.quarantine 文件路径(直接把文件拖入到终端,可以自动找到文件路径)即可令其获得权限 补充知识: 通过gpt可以…...

科技成果鉴定测试如何进行?第三方检测机构进行鉴定测试的好处
科技成果鉴定测试,作为科技领域中一项重要的质量检验手段,具有广泛的应用范围。旨在为科技成果的研发者和使用者提供客观、科学、权威的鉴定结果,从而评估科技成果的技术水平和市场竞争力。 科技成果鉴定测试是对科技成果进行系统、全面的…...
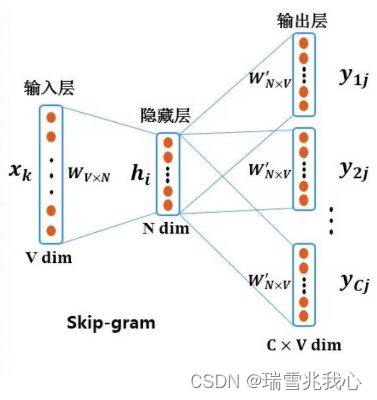
八、词嵌入语言模型(Word Embedding)
词嵌入(Word Embedding, WE),任务是把不可计算、非结构化的词转换为可以计算、结构化的向量,从而便于进行数学处理。 一个更官方一点的定义是:词嵌入是是指把一个维数为所有词的数量的高维空间(one-hot形式…...

重学SpringBoot3-WebMvcConfigurer接口
摘要: 本文详细介绍了SpringBoot 3中的WebMvcConfigurer接口,旨在帮助读者深入理解其原理和实现,从而能够更好地使用SpringBoot进行Web开发。阅读本文需要大约30分钟。 关键词:SpringBoot, WebMvcConfigurer, SpringMVC, Web开发…...
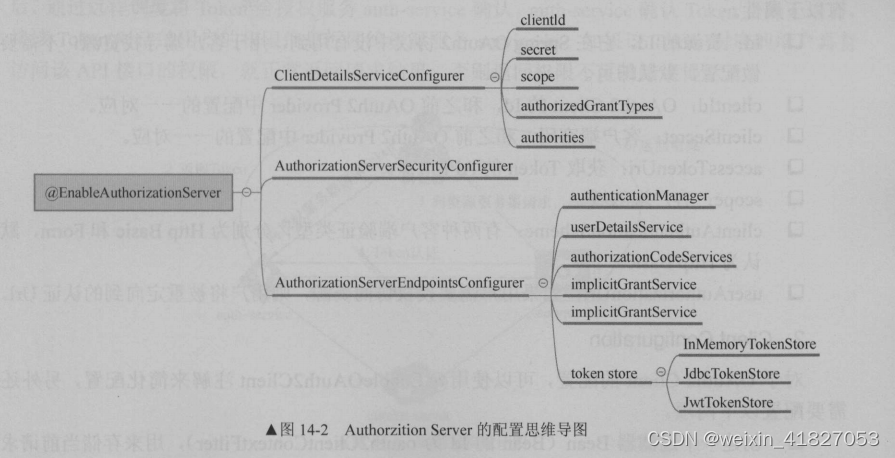
《深入理解springCloud与微服务》笔记
第一章 微服务介绍 1.3 微服务的不足 1.3.2 分布式事务 CAP 理论,即同时满足“一致性”“可用性”和“分区容错”是 件不可能的事。 Consistency :指数据的强一致性。如果写入某个数据成功,之后读取,读到的都是新写入的数据&a…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
