每日构造题训练——C. Divan and bitwise operations
每日构造题训练
题目链接: 题目传送门
前置知识: 按位或运算
一、题意:
1 1 1、 有一个长度为 n n n的但是元素未知的数组 a a a, 给定 m m m个约束,每个约束都有 l , r , x l, r, x l,r,x, 并且满足 1 ≤ l ≤ r ≤ n , 1 ≤ x < 2 30 , a [ l ] ∣ a [ l + 1 ] ∣ . . . . ∣ a [ r ] = x 1 \le l \le r \le n, 1 \le x < 2^{30}, a[l] | a[l + 1] | .... | a[r] = x 1≤l≤r≤n,1≤x<230,a[l]∣a[l+1]∣....∣a[r]=x, l l l是按位或,要求构造出 a a a的 n n n个元素,使得其满足 m m m个约束并且 0 ≤ a [ i ] < 2 30 0 \le a[i] < 2^{30} 0≤a[i]<230,并且求出每个非空子序列(子序列可以不连续,但是要保序)的异或值之和,结果模 1 e 9 + 7 1e9+7 1e9+7, 保证在这些约束下有解。
2 2 2、数据范围: 1 ≤ n ≤ 2 e 5 1 \le n \le 2e5 1≤n≤2e5, 1 ≤ m ≤ 2 e 5 1 \le m \le 2e5 1≤m≤2e5
二、题解:
1 1 1、 我们先思考 ∣ | ∣ 运算的性质,可以知道只要在区间中有一个数字在某个二进制位上是 1 1 1,那么区间的 ∣ | ∣值一定在此二进制位上有 1 1 1,那么我们不妨倒着思考,假设我们知道一个区间的 ∣ | ∣值,我们就可以知道它们在哪些二进制一定是 0 0 0, 怎么根据这些区间记录呢,我们可以用预处理的思想去做,因为暴力去更新显然会超时。
2 2 2、我们可以开一个数组 c n t [ 30 ] [ i ] cnt[30][i] cnt[30][i]用来标记第i个数字上的第 30 30 30个二进制位,当我们读取到查询 l , r , x l,r,x l,r,x时, 我们将数字 x x x中二进制位为 0 0 0的位置找到,假设是 j j j,那么我们就可以用差分处理, c n t [ j ] [ l ] + = 1 , c n t [ j ] [ r + 1 ] − = 1 cnt[j][l] \mathrel{+}= 1, cnt[j][r + 1] \mathrel{-}= 1 cnt[j][l]+=1,cnt[j][r+1]−=1,最后我们就可以用前缀和知道每个数字的每一个二进制位的信息了,此时我们不妨将每一位的初值赋值为 ( 1 < < 30 ) − 1 (1<<30)-1 (1<<30)−1,这样每一个二进制位都有 1 1 1,当我们知道 c n t [ j ] [ i ] > 0 cnt[j][i]>0 cnt[j][i]>0, 则 a [ i ] & = ( 1 < < j ) a[i]\mathrel{\&}= (1<<j) a[i]&=(1<<j)。
3 3 3、根据上面设计的思路我们可以找到满足约束的数组 a a a的每个元素,接下来我们要计算所有的非空子序列异或值之和,我们不妨考虑一下累积每个二进制位的贡献,我们先统计一下每个二进制位的个数 c o u n t [ i ] count[i] count[i],让我们来推导一下计算二进制位贡献的公式,首先只有奇数个 1 1 1异或值才能是 1 1 1, 所以,我们将很轻易的推导出计算贡献的公式: ∑ ( C ( 1 c o u n t [ i ] ) ∗ 2 n − 1 + C ( 3 c o u n t [ i ] ) ∗ 2 n − 3 + . . . + C ( 2 ∗ x + 1 c o u n t [ i ] ) ∗ 2 n − ( 2 ∗ x + 1 ) ) \sum(C\binom{1}{count[i]} * 2^{n-1} + C\binom{3}{count[i]} * 2^{n-3} + ... + C\binom{2 * x + 1}{count[i]}* 2^{n-(2*x+1)}) ∑(C(count[i]1)∗2n−1+C(count[i]3)∗2n−3+...+C(count[i]2∗x+1)∗2n−(2∗x+1))。
4 4 4、时间复杂度(忽略常数): O ( N ∗ 30 + N ∗ l o g ( 2 30 − 1 ) ) O(N * 30 + N * log(2^{30}-1)) O(N∗30+N∗log(230−1))。
三、代码实现:
涉及算法:快速幂、组合数预处理、差分、前缀和、逆元。
#include <bits/stdc++.h>
#define int long long
#define ff first
#define ss second
using namespace std;
using PII = pair<int, int>;
constexpr int N = 2e5 + 10;
constexpr int inf = 0x3f3f3f3f;
constexpr int mod = 1e9 + 7;
int n, m;
int a[N];
int cnt[40][N];
int us[40];
int f1[N], f2[N];
int qmi(int x, int y) {int res = 1; while(y) {if(y & 1) res = res * x % mod; x = x * x % mod; y >>= 1; }return res;
}int md(int a, int b) {return (f1[a] * f2[a - b] % mod * f2[b] % mod) % mod;
}
void solve() {scanf("%lld%lld",&n,&m);// for(int j = 0; j < 40; j ++ ) us[j] = 0; for(int i = 1; i <= n; i ++ ) a[i] = (1 << 30) - 1; for(int i = 0; i < 30; i ++ ) { us[i] = 0; for(int j = 1; j <= n; j ++ ) cnt[i][j] = 0;}for(int i = 1; i <= m; i ++ ) {int l, r, x; scanf("%lld%lld%lld",&l,&r,&x);for(int j = 0; j < 30; j ++ ) {if(x >> j & 1) continue; cnt[j][l] += 1, cnt[j][r + 1] -= 1; }}for(int i = 0; i < 30; i ++ ) {for(int j = 1; j <= n; j ++ ) cnt[i][j] += cnt[i][j - 1]; for(int j = 1; j <= n; j ++ ) if(cnt[i][j]) a[j] -= (1 << i);}for(int i = 1; i <= n; i ++ ) for(int j = 0; j < 30; j ++ ) if(a[i] >> j & 1) us[j] ++; for(int i = 0; i < 30; i ++ ) {int x = us[i], su = 0; // us[i] = 0;for(int j = 1; j <= x; j += 2) su = (su + md(x, j) * qmi(2,n-x) % mod) % mod;us[i] = su;}int ans = 0; for(int i = 0; i < 30; i ++ ) ans = (ans + (1ll << i) * us[i] % mod) % mod;printf("%lld\n",ans);
}signed main() {f1[0] = 1, f2[0] = 1; for(int i = 1; i < N; i ++ ) {f1[i] = (f1[i - 1] * i) % mod; f2[i] = qmi(f1[i], mod - 2);}int ts; cin >> ts; while(ts -- ) solve(); return 0;
}
相关文章:

每日构造题训练——C. Divan and bitwise operations
每日构造题训练 题目链接: 题目传送门 前置知识: 按位或运算 一、题意: 1 1 1、 有一个长度为 n n n的但是元素未知的数组 a a a, 给定 m m m个约束,每个约束都有 l , r , x l, r, x l,r,x, 并且满足 1 ≤ l ≤ r ≤ n , 1 ≤ x < 2 30 , a [ l ] ∣ a [ l 1 …...

【C++练级之路】【Lv.13】多态(你真的了解虚函数和虚函数表吗?)
快乐的流畅:个人主页 个人专栏:《C语言》《数据结构世界》《进击的C》 远方有一堆篝火,在为久候之人燃烧! 文章目录 一、虚函数与重写1.1 虚函数1.2 虚函数的重写1.3 重写的特例1.4 final和override(C11)1.…...

如何在Windows系统安装Node.js环境并制作html页面发布公网远程访问?
文章目录 前言1.安装Node.js环境2.创建node.js服务3. 访问node.js 服务4.内网穿透4.1 安装配置cpolar内网穿透4.2 创建隧道映射本地端口 5.固定公网地址 前言 Node.js 是能够在服务器端运行 JavaScript 的开放源代码、跨平台运行环境。Node.js 由 OpenJS Foundation࿰…...

C#,数值计算,希尔伯特矩阵(Hilbert Matrix)的算法与源代码
Hilbert, David (1862-1943) 1 希尔伯特(Hilbert) 德国数学家,在《几何学基础》中提出了第一套严格的几何公理(1899年)。他还证明了自己的系统是自洽的。他发明了一条简单的空间填充曲线,即埃里克魏斯汀的数学世界,即希尔伯特曲线,埃里克魏斯汀的数学世界,并证明了不…...

【C++教程从0到1入门编程】第八篇:STL中string类的模拟实现
一、 string类的模拟实现 下面是一个列子 #include <iostream> namespace y {class string{public: //string() //无参构造函数// :_str(nullptr)//{}//string(char* str) //有参构造函数// :_str(str)//{}string():_str(new char[1]){_str[0] \0;}string(c…...

学生时期学习资源同步-1 第一学期结业考试题6
原创作者:田超凡(程序员田宝宝) 版权所有,引用请注明原作者,严禁复制转载...

迁移学习怎么用
如果想实现一个计算机视觉应用,而不想从零开始训练权重,比方从随机初始化开始训练,更快的方式是下载已经训练好权重的网络结构,把这个作为预训练,迁移到你感兴趣的新任务上。ImageNet、PASCAL等等数据库已经公开在线。…...

医疗手持智能终端读取条码二维码的难点有哪些?
在医疗科技行业信息化的大潮中,医疗手持式智能终端的应用越发普及,医疗手持式智能终端对条码二维码技术应用显得尤为关键,作为信息朔源载体的条码二维码读取方面,在实际应用中却面临着诸多问题,我们该如何应对…...
Python小设计
1. 五个PPT上的界面打印【print、input函数】 (1)英雄商城登陆界面 print(英雄联盟商城登录界面 ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~1. 用户登录2. 新用户注册3. 退出系统 ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~…...

今日讲讲父子传值~
今天来讲讲父子传值中的几种方法~ 项目中往往会把一些常用的公共代码抽离出来,写成一个子组件。或者在一个页面中的代码太多,可以根据功能的不同抽离出相关代码写成子组件,这样代码结构会更加简洁明了,后续维护更加方便。…...
三、HarmonyOS 应用开发入门之运行Hello World
目录 1、课程对象 1.1、有移动端开发经验 1.2、无移动端开发经验 1.3、对 HarmonyOS 感兴趣 2、DevEco Studio 的使用 2.1、DevEco Studio 的关键特性 智能代码编辑 低代码开发 多段双向实时预览 多端模拟仿真 2.2、安装配置 DevEco Studio 2.2.1、官网开发工具下载地…...
国科大网络行为学导论代码作业--更新中
一、Xray安装 参考自:Xray的安装与使用(超详细)_xray使用教程-CSDN博客 下载网址:Releases chaitin/xray GitHub 解压 双击安装 生成证书 cd到xray目录,生成证书 复制链接 然后cd到xray目录 .\xray_windows_amd6…...
——SpringBoot)
JAVA后端开发面试基础知识(九)——SpringBoot
启动原理 SpringBoot启动非常简单,因其内置了Tomcat,所以只需要通过下面几种方式启动即可: @SpringBootApplication(scanBasePackages = {"cn.dark"}) public class SpringbootDemo {public static void main(String[] args) {// 第一种SpringApplication.run(S…...
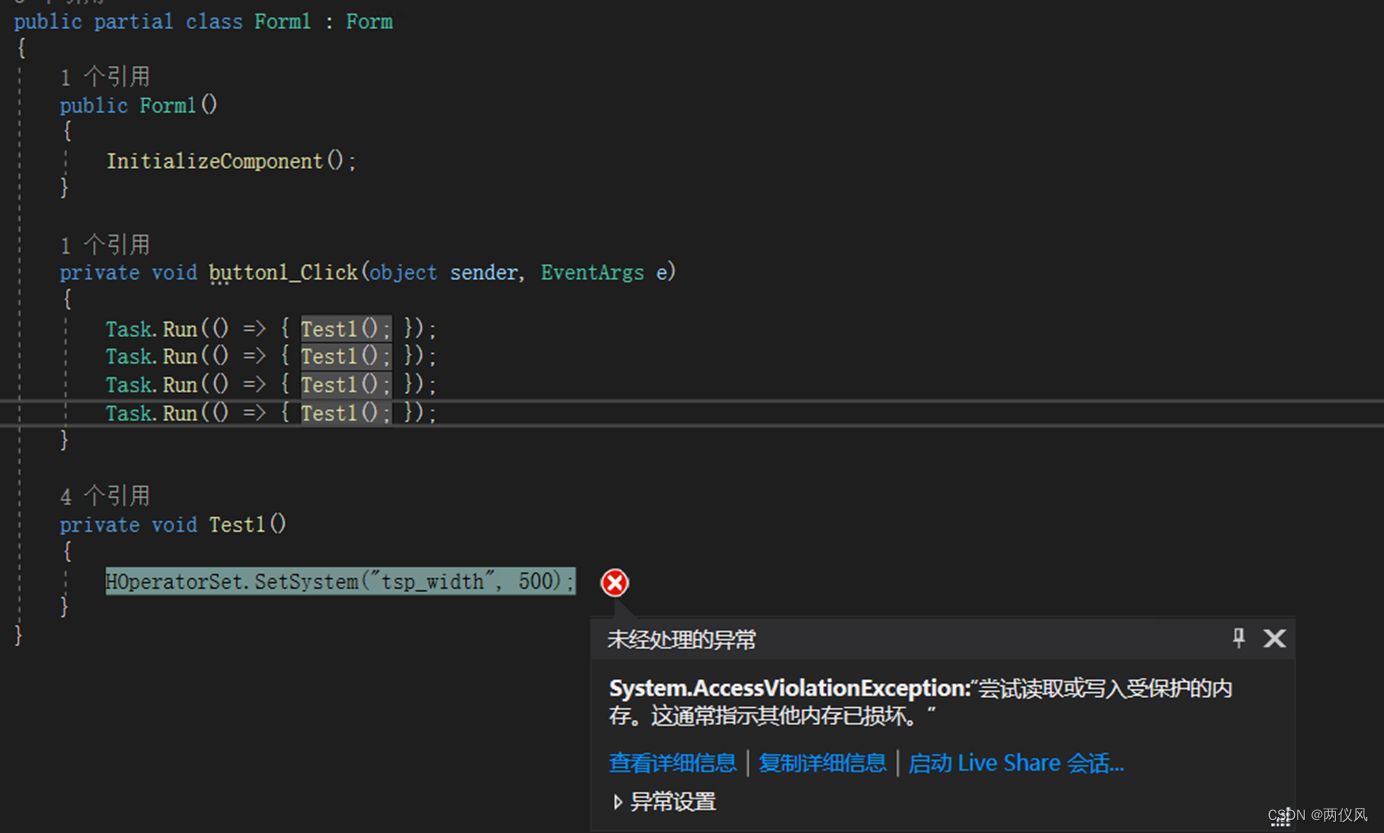
C#调用Halcon出现尝试读取或写入受保护的内存,这通常指示其他内存已损坏。System.AccessViolationException
一、现象 在C#中调用Halcon,出现异常提示:尝试读取或写入受保护的内存,这通常指示其他内存已损坏。System.AccessViolationException 二、原因 多个线程同时访问Halcon中的某个公共变量,导致程序报错 三、测试 3.1 Halcon代码 其中tsp_width…...

ts基础知识
1. any 类型,unknown 类型,never 类型 TypeScript 有两个“顶层类型”(any和unknown),但是“底层类型”只有never唯一一个 1、any 1.1 基本含义 any 类型表示没有任何限制,该类型的变量可以赋予任意类型的…...

KLayout Python Script ------ 绘制1个 Box 物体
KLayout Python Script ------ 绘制两个 Box 物体 引言正文引言 本人通常使用 IPKISS 进行版图绘制,然而很多时候,IPKISS 的功能十分鸡肋。因此,萌生了一种自己写绘制软件的想法,因为 IPKISS 绘制的版图最终也是使用 KLayout 来呈现的,因此,再研究了 KLayout 提供的 API…...

c# 编辑、删除一条数据
1、编辑数据 [HttpPost] public MessageModel<string> Put([FromBody] Dtable request) { var data new MessageModel<string>(); request.UPDATETIME DateTime.Now; if (request.ID>0) { …...

高性能服务系列【八】C10M时代,网络IO库需要重建
在目前网络上能搜索到的,关于网络IO模型的文章,基本都是关于多路复用的iocp/epoll的,这些技术是为了解决C10K问题而提出的解决方案。现代网卡已经普遍支持10Gb,100Gb也不少见,这些解决方案已经无法提升性能的需求。 我…...

Go语言与Rust哪一个更有发展前景?
Go语言和Rust都是目前非常受欢迎的编程语言,它们各自具有独特的优势和适用场景。关于哪一个更有发展前景,这实际上取决于多个因素,包括个人偏好、项目需求、社区支持以及未来技术的发展趋势等。 Go语言是由Google推出的,具有简洁…...

STM32使用定时器驱动电机
STM32使用定时器驱动电机 1、对定时器进行初始化配置1.1、include "encoder.c"文件 主函数 1、对定时器进行初始化配置 1.1、include "encoder.c"文件 #include "encoder.h"void TIM4_Encoder_Init(u16 arr,u16 psc) { GPIO_InitTypeDef GPIO…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...
