用python实现Dubins曲线生成
Dubins曲线是连接两个具有指定方向和位置的点的最短路径,其中路径受到固定曲率约束(如车辆的转向限制)。Dubins曲线常用于机器人路径规划、车辆轨迹规划等领域。
Dubins曲线可以分为三种类型:CCC (Curve-Curve-Curve), CCL (Curve-Curve-Line), LLC (Line-Line-Curve),其中C表示曲线段(转弯),L表示直线段(直行)。生成Dubins曲线需要确定起始点和终止点的位置、方向以及最大曲率。
下面是一个简单的Python实现,用于生成Dubins曲线的LLC类型。这个实现仅考虑了2D情况,且假定最大曲率恒定。
python
复制代码
import numpy as np
import matplotlib.pyplot as plt
class DubinsPath:
def __init__(self, qx, qy, qtheta, qx_f, qy_f, qtheta_f, rho):
self.qx = qx
self.qy = qy
self.qtheta = qtheta
self.qx_f = qx_f
self.qy_f = qy_f
self.qtheta_f = qtheta_f
self.rho = rho
self.calculate_path()
def calculate_path(self):
# 这里只实现了LLC类型的Dubins曲线
# 直线段到曲线段
theta_mid = (self.qtheta + self.qtheta_f) / 2
delta_s = np.sqrt((self.qx_f - self.qx) ** 2 + (self.qy_f - self.qy) ** 2)
delta_theta = np.abs(self.qtheta_f - self.qtheta)
sigma = delta_s / (2 * self.rho)
# 计算中间点
if delta_theta > np.pi:
theta_mid = theta_mid - np.pi
cx = self.qx + self.rho * np.sin(theta_mid)
cy = self.qy - self.rho * np.cos(theta_mid)
# 直线段
dx = cx - self.qx
dy = cy - self.qy
t = np.linspace(0, 1, 100)
self.x_line = self.qx + dx * t
self.y_line = self.qy + dy * t
# 曲线段
phi = theta_mid - np.arctan2(dy, dx)
s = np.linspace(0, sigma, 100)
self.x_curve = cx + self.rho * (np.cos(phi) - np.sin(phi) * np.tanh(s))
self.y_curve = cy + self.rho * (np.sin(phi) + np.cos(phi) * np.tanh(s))
# 直线段到曲线段的过渡点
self.x_transition = self.x_curve[0]
self.y_transition = self.y_curve[0]
def plot_path(self):
plt.figure(figsize=(8, 6))
plt.plot(self.x_line, self.y_line, label='Line Segment')
plt.plot(self.x_curve, self.y_curve, label='Curve Segment')
plt.scatter(self.qx, self.qy, color='red', label='Start')
plt.scatter(self.qx_f, self.qy_f, color='blue', label='End')
plt.scatter(self.x_transition, self.y_transition, color='green', label='Transition')
plt.axis('equal')
plt.grid(True)
plt.legend()
plt.show()
# 使用示例
if __name__ == "__main__":
# 初始和终止位置及方向
qx, qy = 0, 0
qtheta = np.pi / 4
qx_f, qy_f = 10, 10
qtheta_f = 3 * np.pi / 4
# 最大曲率(这里用曲率半径的倒数表示)
rho = 1.0
dubins_path = DubinsPath(qx, qy, qtheta, qx_f, qy_f, qtheta_f, rho)
相关文章:

用python实现Dubins曲线生成
Dubins曲线是连接两个具有指定方向和位置的点的最短路径,其中路径受到固定曲率约束(如车辆的转向限制)。Dubins曲线常用于机器人路径规划、车辆轨迹规划等领域。 Dubins曲线可以分为三种类型:CCC (Curve-Curve-Curve), CCL (Curv…...

智能技术上的“是”并不代表具体领域的“应该”
技术上的“是”并不代表具体领域的“应该” 。技术上的“是”仅仅是指某种方法或技术在实践中是否可行或有效,而不涉及是否该采取这种方法或技术。决定是否采取某种方法或技术还需要考虑伦理、法律、可行性等其他方面的因素。技术的发展可能会有各种可能性ÿ…...

永热爱 敢向前 | Paraverse平行云的2023 年终总结
永热爱,敢向前 值此新年,回顾2023,仅以此句,献给所有XR产业信仰者 2023 年,是XR产业技术和场景承上启下的关键之年 在这场波澜壮阔的技术潮中 「Paraverse平行云」踏浪前行 已是第八个年头,让我们一起…...

c/c++的内存分配,详细说一下栈、堆和静态存储区
栈区(Stack):由编译器自动分配和回收,栈中存放函数调用的相关信息,栈帧(记录函数的栈帧开始的位置),参数,局部变量,返回地址。其操作方法类似于数据结构中的栈…...

每日构造题训练——C. Divan and bitwise operations
每日构造题训练 题目链接: 题目传送门 前置知识: 按位或运算 一、题意: 1 1 1、 有一个长度为 n n n的但是元素未知的数组 a a a, 给定 m m m个约束,每个约束都有 l , r , x l, r, x l,r,x, 并且满足 1 ≤ l ≤ r ≤ n , 1 ≤ x < 2 30 , a [ l ] ∣ a [ l 1 …...

【C++练级之路】【Lv.13】多态(你真的了解虚函数和虚函数表吗?)
快乐的流畅:个人主页 个人专栏:《C语言》《数据结构世界》《进击的C》 远方有一堆篝火,在为久候之人燃烧! 文章目录 一、虚函数与重写1.1 虚函数1.2 虚函数的重写1.3 重写的特例1.4 final和override(C11)1.…...

如何在Windows系统安装Node.js环境并制作html页面发布公网远程访问?
文章目录 前言1.安装Node.js环境2.创建node.js服务3. 访问node.js 服务4.内网穿透4.1 安装配置cpolar内网穿透4.2 创建隧道映射本地端口 5.固定公网地址 前言 Node.js 是能够在服务器端运行 JavaScript 的开放源代码、跨平台运行环境。Node.js 由 OpenJS Foundation࿰…...

C#,数值计算,希尔伯特矩阵(Hilbert Matrix)的算法与源代码
Hilbert, David (1862-1943) 1 希尔伯特(Hilbert) 德国数学家,在《几何学基础》中提出了第一套严格的几何公理(1899年)。他还证明了自己的系统是自洽的。他发明了一条简单的空间填充曲线,即埃里克魏斯汀的数学世界,即希尔伯特曲线,埃里克魏斯汀的数学世界,并证明了不…...

【C++教程从0到1入门编程】第八篇:STL中string类的模拟实现
一、 string类的模拟实现 下面是一个列子 #include <iostream> namespace y {class string{public: //string() //无参构造函数// :_str(nullptr)//{}//string(char* str) //有参构造函数// :_str(str)//{}string():_str(new char[1]){_str[0] \0;}string(c…...

学生时期学习资源同步-1 第一学期结业考试题6
原创作者:田超凡(程序员田宝宝) 版权所有,引用请注明原作者,严禁复制转载...

迁移学习怎么用
如果想实现一个计算机视觉应用,而不想从零开始训练权重,比方从随机初始化开始训练,更快的方式是下载已经训练好权重的网络结构,把这个作为预训练,迁移到你感兴趣的新任务上。ImageNet、PASCAL等等数据库已经公开在线。…...

医疗手持智能终端读取条码二维码的难点有哪些?
在医疗科技行业信息化的大潮中,医疗手持式智能终端的应用越发普及,医疗手持式智能终端对条码二维码技术应用显得尤为关键,作为信息朔源载体的条码二维码读取方面,在实际应用中却面临着诸多问题,我们该如何应对…...
Python小设计
1. 五个PPT上的界面打印【print、input函数】 (1)英雄商城登陆界面 print(英雄联盟商城登录界面 ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~1. 用户登录2. 新用户注册3. 退出系统 ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~ * ~…...

今日讲讲父子传值~
今天来讲讲父子传值中的几种方法~ 项目中往往会把一些常用的公共代码抽离出来,写成一个子组件。或者在一个页面中的代码太多,可以根据功能的不同抽离出相关代码写成子组件,这样代码结构会更加简洁明了,后续维护更加方便。…...
三、HarmonyOS 应用开发入门之运行Hello World
目录 1、课程对象 1.1、有移动端开发经验 1.2、无移动端开发经验 1.3、对 HarmonyOS 感兴趣 2、DevEco Studio 的使用 2.1、DevEco Studio 的关键特性 智能代码编辑 低代码开发 多段双向实时预览 多端模拟仿真 2.2、安装配置 DevEco Studio 2.2.1、官网开发工具下载地…...
国科大网络行为学导论代码作业--更新中
一、Xray安装 参考自:Xray的安装与使用(超详细)_xray使用教程-CSDN博客 下载网址:Releases chaitin/xray GitHub 解压 双击安装 生成证书 cd到xray目录,生成证书 复制链接 然后cd到xray目录 .\xray_windows_amd6…...
——SpringBoot)
JAVA后端开发面试基础知识(九)——SpringBoot
启动原理 SpringBoot启动非常简单,因其内置了Tomcat,所以只需要通过下面几种方式启动即可: @SpringBootApplication(scanBasePackages = {"cn.dark"}) public class SpringbootDemo {public static void main(String[] args) {// 第一种SpringApplication.run(S…...
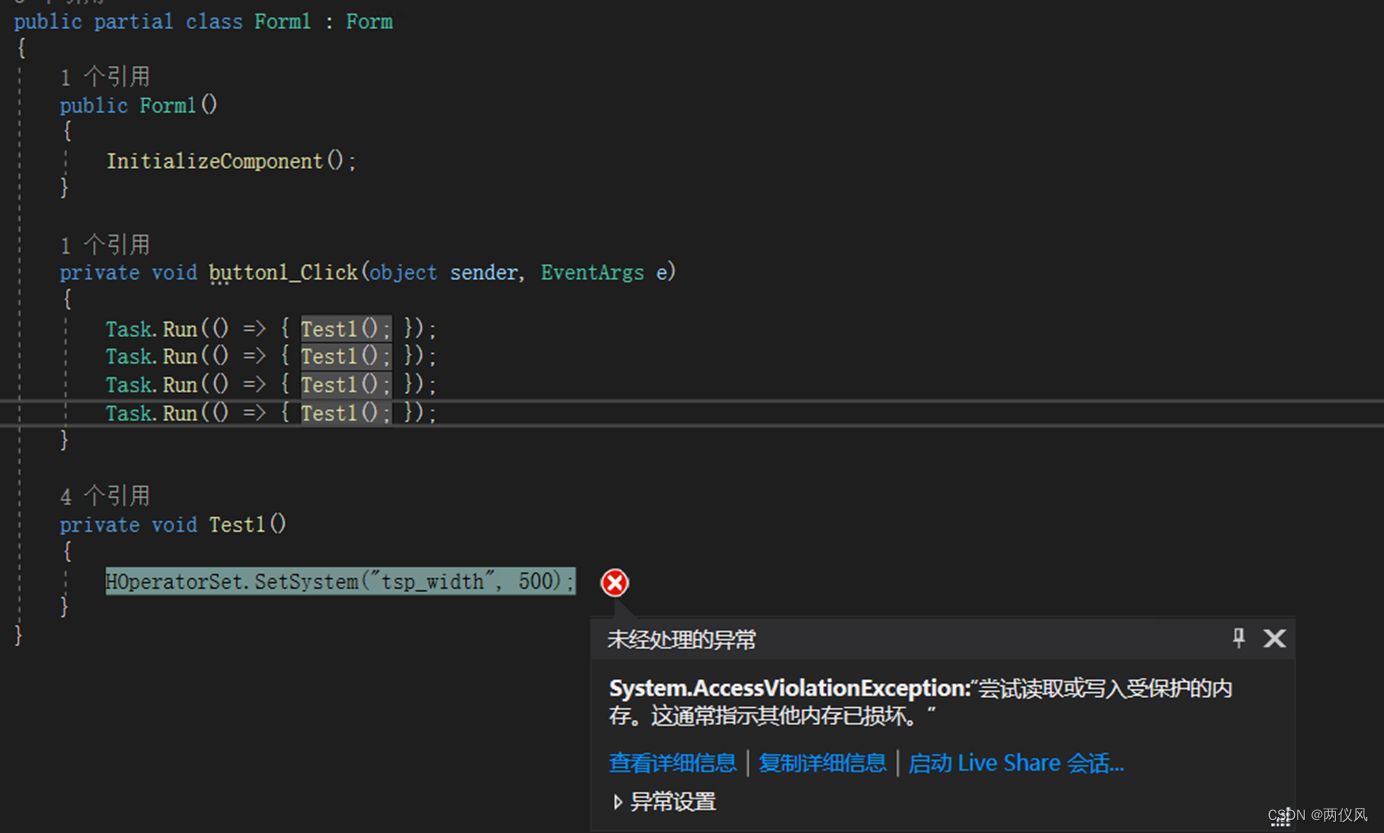
C#调用Halcon出现尝试读取或写入受保护的内存,这通常指示其他内存已损坏。System.AccessViolationException
一、现象 在C#中调用Halcon,出现异常提示:尝试读取或写入受保护的内存,这通常指示其他内存已损坏。System.AccessViolationException 二、原因 多个线程同时访问Halcon中的某个公共变量,导致程序报错 三、测试 3.1 Halcon代码 其中tsp_width…...

ts基础知识
1. any 类型,unknown 类型,never 类型 TypeScript 有两个“顶层类型”(any和unknown),但是“底层类型”只有never唯一一个 1、any 1.1 基本含义 any 类型表示没有任何限制,该类型的变量可以赋予任意类型的…...

KLayout Python Script ------ 绘制1个 Box 物体
KLayout Python Script ------ 绘制两个 Box 物体 引言正文引言 本人通常使用 IPKISS 进行版图绘制,然而很多时候,IPKISS 的功能十分鸡肋。因此,萌生了一种自己写绘制软件的想法,因为 IPKISS 绘制的版图最终也是使用 KLayout 来呈现的,因此,再研究了 KLayout 提供的 API…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
