*地宫取宝c++
题目

输入样例1:
2 2 2
1 2
2 1
输出样例1:
2
输入样例2:
2 3 2
1 2 3
2 1 5
输出样例2:
14思路
题目说从入口开始,只能向右或向下行走到达右下角,类似“摘花生”这道题的模型。题目又说只有当格子里的宝贝价值比小明手中任意宝贝价值都大,小明就可以拿起它,也就说拿到的宝贝价值严格单调递增,是“单调递增子序列”的模型。
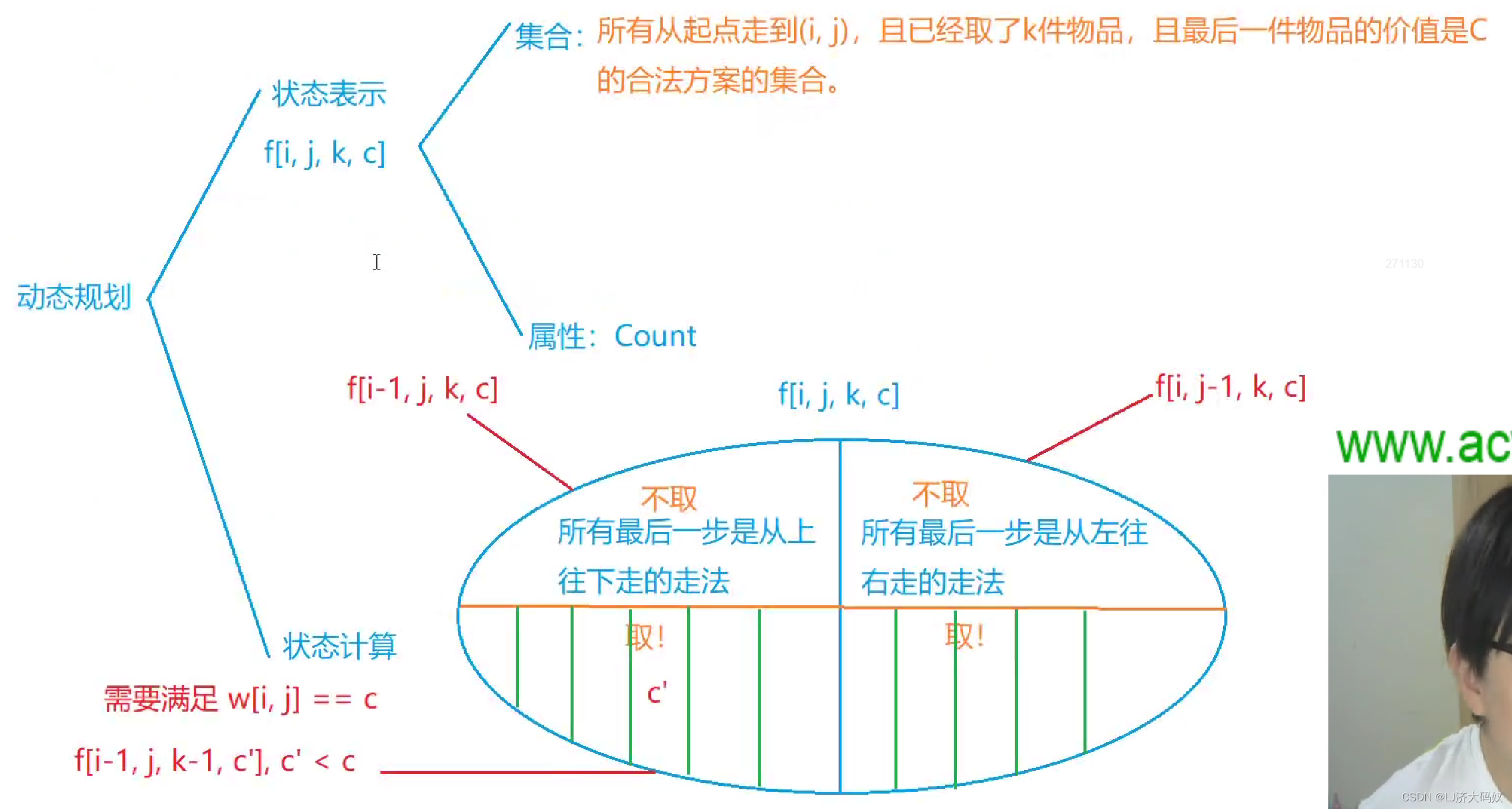
状态表示:
那用几维才能表示一个状态呢?首先,需要用 i, j 来表示从起点走到 (i, j) 这个格子的所有路径方案数;然后,需要用ki来表示从起点走到(i, j)这个格子拿了多少个物品;最后,由于拿到的宝贝价值要严格单调递增,因此需要用C表示拿到的最后一个物品的价值。
那为什么我们不用最后一个物品的坐标来表示状态呢,通过坐标也可以得到最后一个物品的价值啊?因为有50 x 50个坐标,并且是这样做会使一个状态表示的维数达到五维,时间复杂度也会增加。题目中取到宝贝的价值有限(0≤Ci≤12),因此可以用C代表最后取到的宝贝的最大值即可,这样可以将维数降到四维。
综上所述,我们可以将集合f[i][j][ki][c]定义为所有从起点走到(i,j),且已经取了ki件物品,且最后一件物品的价值是C的合法方案的集合。集合属性为满足集合定义的方案数总和。
状态计算:
由于到达(i, j)这个点只能从左边或上边来,因此可以将集合划分为所有最后一步是从上往下走的走法的集合和所有最后一步是从左往右走的走法的集合。而对于所有最后一步是从上往下走的走法的集合,又可以划分为取不取(i, j)这个格子的宝贝这两个小的集合,当要取(i, j)这个格子的宝贝时,说明这个格子里宝贝价值value比前面拿到的任何宝贝的价值都大,并且,根据集合定义,f[i][j][ki][c]存的是最后一件物品的价值是c的合法方案的集合,因此,当枚举c时,若要取(i, j)这个格子的宝贝还需要满足value等于c。
边界处理
需要注意的是,由于宝贝的价值可能为0,当左上角格子的的宝贝价值为0时,不拿可以表示为f[1][1][0][0] = 1,但下一步(向右或向下走)遇到一个格子的宝贝价值为0,就不能拿了,因为题目要求拿到的宝贝价值要严格单调递增;而实际上,若没有拿左上角格子价值为0的宝贝,在下一步遇到一个价值为0的宝贝是可以选择拿或不拿的。
对此,我们可以将所有格子里宝贝的价值都加上1,宝贝价值区间变成1≤Ci≤13;当c为0时表示还没有拿过任何一件宝贝,“最后一个物品价值为0”。这样处理后,当左上角格子的的宝贝价值为1时,不拿可以表示为f[1][1][0][0] = 1,当下一步(向右或向下走)遇到一个格子的宝贝价值为1,就可以选择拿或不拿了。
int 范围为2.1 x 10^9,因此val最多加两个数就要取模了。
代码
#include<bits/stdc++.h>
using namespace std;
const int MOD = 1000000007, N = 55;
int a[N][N], f[N][N][13][14];
int n, m, k, res;int main()
{cin >> n >> m >> k;for (int i = 1; i <= n; i ++){for (int j = 1; j <= m; j ++){cin >> a[i][j];a[i][j] ++;}}int res = 0;f[1][1][1][a[1][1]] = 1, f[1][1][0][0] = 1;for (int i = 1; i <= n; i ++){for (int j = 1; j <= m; j ++){if (i == 1 && j == 1) continue;for (int ki = 0; ki <= k; ki ++){for (int value = 0; value <= 13; value ++){int &val = f[i][j][ki][value];//不能选(i, j)这个格子里的宝贝//从上往下走,并且不取(i, j)上的宝贝的方案数val = (val + f[i - 1][j][ki][value]) % MOD;//从左往右走,并且不取(i, j)上的宝贝的方案数val = (val + f[i][j - 1][ki][value]) % MOD;if (ki > 0 && value == a[i][j]){for (int c = 0; c < value; c ++){//从前面的状态中选价值c < value并且选了ki - 1件的fval = (val + f[i - 1][j][ki - 1][c]) % MOD;val = (val + f[i][j - 1][ki - 1][c]) % MOD;}}}}}}for (int i = 1; i <= 13; i ++) res = (res + f[n][m][k][i]) % MOD;cout << res;return 0;
}
感觉DP就是根据集合定义打好表,算出全部的状态的值,然后查询表中符合题目要求的状态值。
相关文章:

*地宫取宝c++
题目 输入样例1: 2 2 2 1 2 2 1输出样例1: 2输入样例2: 2 3 2 1 2 3 2 1 5输出样例2: 14 思路 题目说从入口开始,只能向右或向下行走到达右下角,类似“摘花生”这道题的模型。题目又说只有当格子里的宝…...
同态滤波算法详解
同态滤波是一种用于增强图像的方法,特别适用于去除图像中的照明不均和阴影。该算法基于照射反射模型,将图像分解为两个分量:照射分量(illumination component)和反射分量(reflection component)…...

财务管理系统报账和挂账分别什么区别!报销又是什么【第三期】
前言 已经写了两期 财务管理系统之saas多租户架构是什么以及分库分表以及如何选择分布式事务方案 【程序员聊业务】财务管理系统之模块分类 报账和挂账概念 报账是指企业或个人因业务需要而发生的各项费用支出,在支付后,需要将相关的票据、凭证等提交…...

最少刷题数
最少刷题数 题目分析 对于每一名同学计算还需要再刷多少题才能保证刷题数比他多的人数不超过刷题数比他少的学生人数。我们可以考虑统计每一个分数的前缀和数组,sum[i]表示当前学生中,刷题数小于等于i的人数。那么对于学生i的刷题数a[i],su…...

Python刘诗诗
写在前面 刘诗诗在电视剧《一念关山》中饰演了女主角任如意,这是一个极具魅力的女性角色,她既是一位有着高超武艺和智慧的女侠士,也曾经是安国朱衣卫前左使,身怀绝技且性格坚韧不屈。剧中,任如意因不满于朱衣卫的暴行…...

探索ChatGPT在软件架构师工作中的应用
随着人工智能技术的不断发展,自然语言处理模型如OpenAI的ChatGPT已经成为了解决各种实际问题的强大工具之一。在软件架构师这个领域,ChatGPT也有着广泛的应用。本文将探讨软件架构师如何有效地利用ChatGPT来解决问题和提高工作效率。 ChatGPT简介 Chat…...

pytest--allure报告中添加用例详情
前言 前面介绍了如何生成allure的报告,看着allure的页面非常好看,但是感觉少了一些内容,allure还可以增加一些用例详情内容,这样让我们的报告看着更加绚丽。 allure增加用例详情 我们可以在报告测试套件中增加用例详情内容。 …...

【深度学习笔记】9_5 多尺度目标检测
注:本文为《动手学深度学习》开源内容,部分标注了个人理解,仅为个人学习记录,无抄袭搬运意图 9.5 多尺度目标检测 在9.4节(锚框)中,我们在实验中以输入图像的每个像素为中心生成多个锚框。这些…...
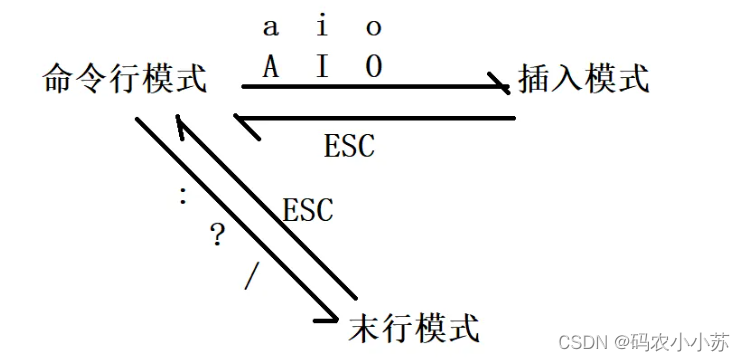
Linux--vim
一.什么是vim Vim(Vi IMproved)是一种文本编辑器,通常在Linux和其他类Unix操作系统中使用。它是Vi编辑器的增强版本,提供了更多的功能和定制选项。Vim具有强大的文本编辑和编程功能,支持语法高亮、代码折叠、宏录制、…...
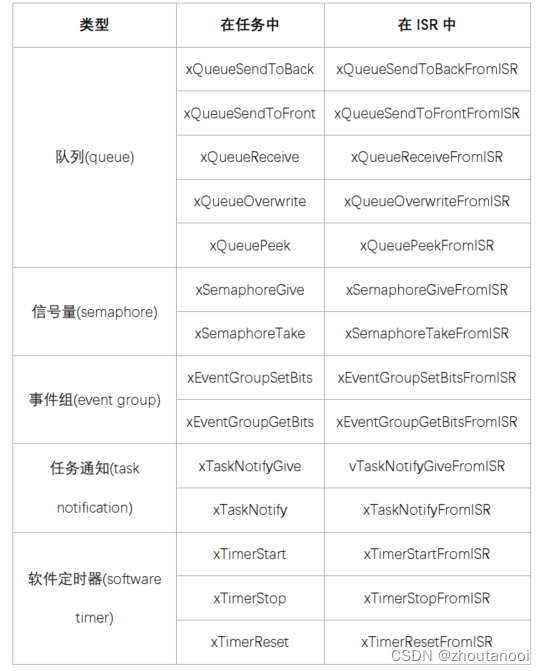
FreeRTOS操作系统学习——中断管理
中断管理介绍 嵌入式实时系统需要对整个系统环境产生的事件作出反应。这些事件对处理时间和响应时间都有不同的要求。事件通常采用中断方式检测,中断服务例程(ISR)中的处理量应当越短越好。ISR是在内核中被调用的, ISR执行过程中,用户的任务…...
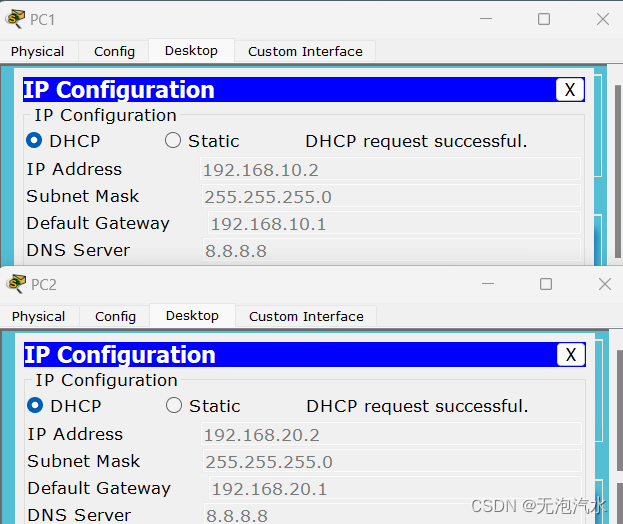
DHCP中继实验(思科)
华为设备参考:DHCP中继实验(华为) 一,技术简介 DHCP中继,可以实现在不同子网和物理网段之间处理和转发DHCP信息的功能。如果DHCP客户机与DHCP服务器在同一个物理网段,则客户机可以正确地获得动态分配的IP…...
基于SpringBoot的“心灵治愈交流平台”的设计与实现(源码+数据库+文档+PPT)
基于SpringBoot的“心灵治愈交流平台”的设计与实现(源码数据库文档PPT) 开发语言:Java 数据库:MySQL 技术:SpringBoot 工具:IDEA/Ecilpse、Navicat、Maven 系统展示 系统功能界面图 登录、用户注册界面图 心灵专…...
【SpringBoot】自定义工具类实现Excel数据新建表存入MySQL数据库
🏡浩泽学编程:个人主页 🔥 推荐专栏:《深入浅出SpringBoot》《java对AI的调用开发》 《RabbitMQ》《Spring》《SpringMVC》《项目实战》 🛸学无止境,不骄不躁,知行合一 文章目录 …...

Retelling|Facebook1
录音 Facebook 1 Retelling|Facebook1 复述转写 Today Im totally going to talk about Facebook. The aspects of this (its)rising fame and fortune, and the rise (小停顿)in(rising) fame and fortune of s founder Mark Zuckerberg, Mark Zuckerberg created this plat…...

【2024-03-12】设计模式之模板模式的理解
实际应用场景:制作月饼 过程描述: 一开始,由人工制作月饼, 第一个:根据脑子里面月饼的形状,先涅出月饼的形状,然后放入面粉和馅料把开口合并起来。 第二个:根据脑子里面月饼的形状&…...

Transformer模型引领NLP革新之路
在不到4 年的时间里,Transformer 模型以其强大的性能和创新的思想,迅速在NLP 社区崭露头角,打破了过去30 年的记录。BERT、T5 和GPT 等模型现在已成为计算机视觉、语音识别、翻译、蛋白质测序、编码等各个领域中新应用的基础构件。因此&#…...

【Kotlin】运算符函数、解构函数、中缀函数
1 一元运算符 1.1 符号和函数 符号函数aa.unaryPlus()-aa.unaryMinus()!aa.not()aa.dec()a--a.inc() 1.2 案例 fun main() {var stu Student("Tom", 13)println(-stu) // 打印: [moT, 31] }class Student(var name: String, var age: Int) {operator fun unaryM…...
springboot268码头船只货柜管理系统
码头船只出行和货柜管理系统的设计与实现 摘要 针对于码头船只货柜信息管理方面的不规范,容错率低,管理人员处理数据费工费时,采用新开发的码头船只货柜管理系统可以从根源上规范整个数据处理流程。 码头船只货柜管理系统能够实现货柜管理…...

Java面试题11MySQL之执行计划到事务及慢查询
你对MySQL执行计划怎么看 执行计划就是SQL的执行查询的顺序,以及如何使用索引查询,返回的结果集的行数 在MySQL中,我们可以通过explain命令来查看执行计划。其语法如下: EXPLAIN SELECT * FROM table_name WHERE conditions;在…...
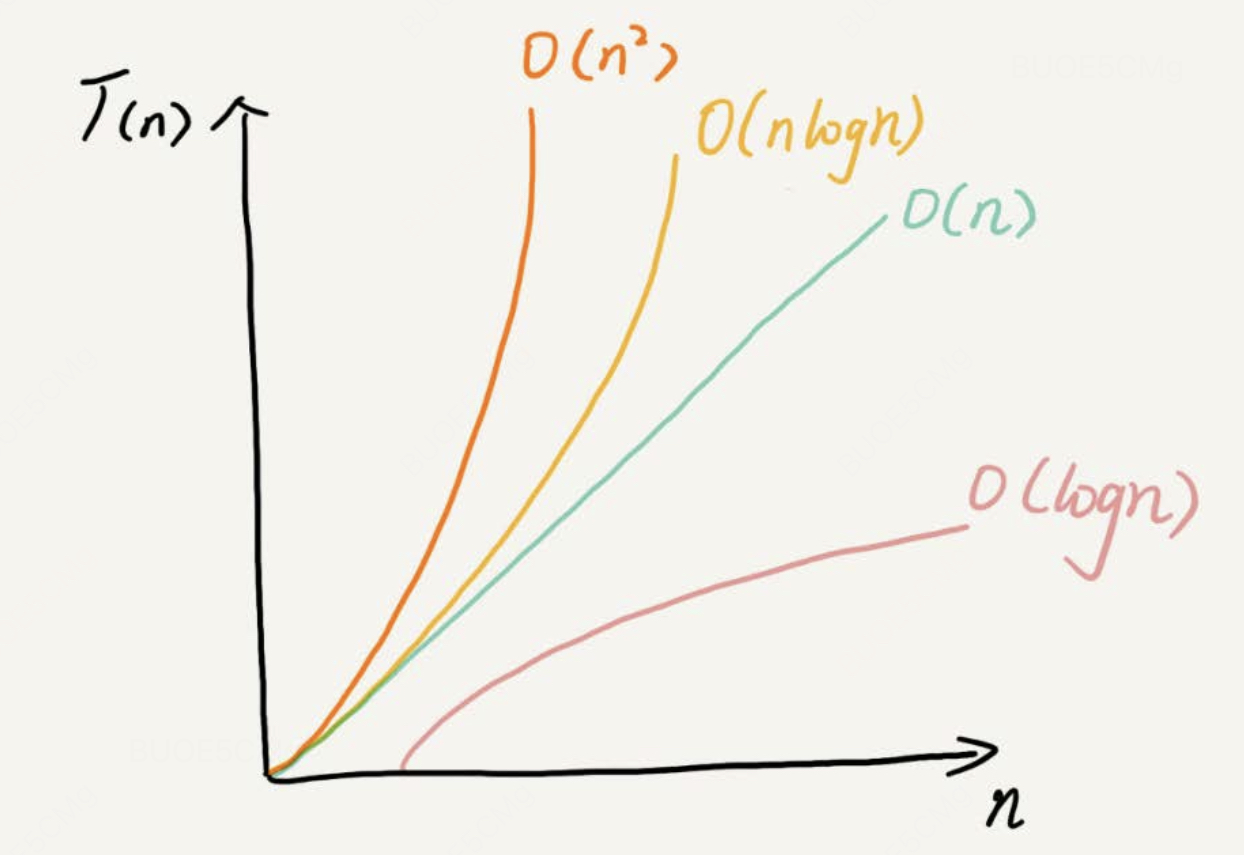
算法时空复杂度分析:大O表示法
文章目录 前言大O表示法3个时间复杂度分析原则常见的时间复杂度量级空间复杂度参考资料 前言 算法题写完以后,面试官经常会追问一下你这个算法的时空复杂度是多少?(好像作为一名算法工程师,我日常码代码的过程中,并没…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
