算法时空复杂度分析:大O表示法
文章目录
- 前言
- 大O表示法
- 3个时间复杂度分析原则
- 常见的时间复杂度量级
- 空间复杂度
- 参考资料
前言
算法题写完以后,面试官经常会追问一下你这个算法的时空复杂度是多少?(好像作为一名算法工程师,我日常码代码的过程中,并没有太注意这个,惭愧~但是找做后端开发的男票求证了一下,他们日常工作确实会去考虑这种问题)那么无论是为了应付面试,还是为了未来码代码可以精益求精,都还是认真的学一下时空复杂度分析方法吧!
对于为什么需要时空复杂度分析,而不是直接跑一下代码看看,看到王争大佬在《数据结构与算法之美》(墙推)里给的两个原因是:
- 测试结果依赖测试环境:机器的配置会十分影响你跑出的结果;
- 测试结果依赖数据规模的大小。
因此,我们需要一个不依赖数据规模和测试环境,帮助粗略估计算法执行效率的方法!也就是下面的大O表示法~
大O表示法
举个栗子🌰,下面这个函数的总的执行时间 T ( n ) = 1 + 2 n T(n) = 1+2n T(n)=1+2n个unit time!
def f(n: int)a = 0 # 1个unit timefor i in range(n): # n个unit timea += i # n个unit timereturn a
再举个栗子🌰,下面这个函数的总的执行时间 T ( n ) = 1 + n + 2 n 2 T(n) = 1+n+2n^2 T(n)=1+n+2n2个unit time!
def g(n: int, m: int)a = 0 # 1个unit timefor i in range(n): # n个unit timefor j in range(n): # n^2个unit timea += i*j # n^2个unit timereturn a
用一个公式表示就是:
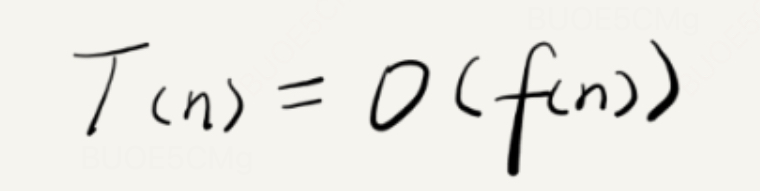
其中:
- T ( n ) T(n) T(n)表示代码执行的时间;
- n n n:表示数据规模的大小;
- f ( n ) f(n) f(n):表示每行代码执行的次数总和
- O O O:表示执行时间 T ( n ) T(n) T(n)与 f ( n ) f(n) f(n)成正比。
所以第一个例子的时间复杂度为 T ( n ) = 1 + 2 n T(n) = 1+2n T(n)=1+2n,第二个例子的时间复杂度为 T ( n ) = 1 + n + 2 n 2 T(n) = 1+n+2n^2 T(n)=1+n+2n2,这就是大O时间复杂度表示法。大O时间复杂度表示法实际上并不是具体值代码执行的时间,而是代表代码执行时间随着数据规模增长的变化趋势,所以也叫渐进时间复杂度,简称时间复杂度。
当n很大时,公式中的低阶、常量、系数三部分并不左右增长趋势,所以都可以忽略,只需要记录一个最大量级即可!因此,上例的时间复杂度可以记为: T ( n ) = O ( n ) T(n) = O(n) T(n)=O(n)、 T ( n ) = O ( n 2 ) T(n) = O(n^2) T(n)=O(n2)。
3个时间复杂度分析原则
3个原则:
1. 只关注循环执行次数最多的一段代码:
还是上面第一个例子,关注for循环这段代码就行了,a = 0这类代码都是常量级的执行时间,与 n n n无关。
def f(n: int)a = 0 # 1个unit timefor i in range(n): # n个unit timea += i # n个unit timereturn a
2. 总复杂度 = 量级最大的那段代码的复杂度:
这个有点像运筹学里关键路径法的思想,只有找到了最关键/量级最大的,你去优化的时候才能发力在刀刃上~
比如下面这段代码,有一层for循环的,有两层for循环,我们去关注两层for循环的这段代码即可。
def g(n: int, m: int)for i in range(n):passa = 0 # 1个unit timefor i in range(n): # n个unit timefor j in range(n): # n^2个unit timea += i*j # n^2个unit timereturn a
3. 嵌套代码的复杂度 = 嵌套内外代码复杂度的乘积:
上面的第二个例子,两层for循环嵌套,最后的时间复杂度 = 外层for循环的复杂度乘以里面for循环的复杂度。
def g(n: int, m: int)a = 0 # 1个unit timefor i in range(n): # n个unit timefor j in range(n): # n^2个unit timea += i*j # n^2个unit timereturn a
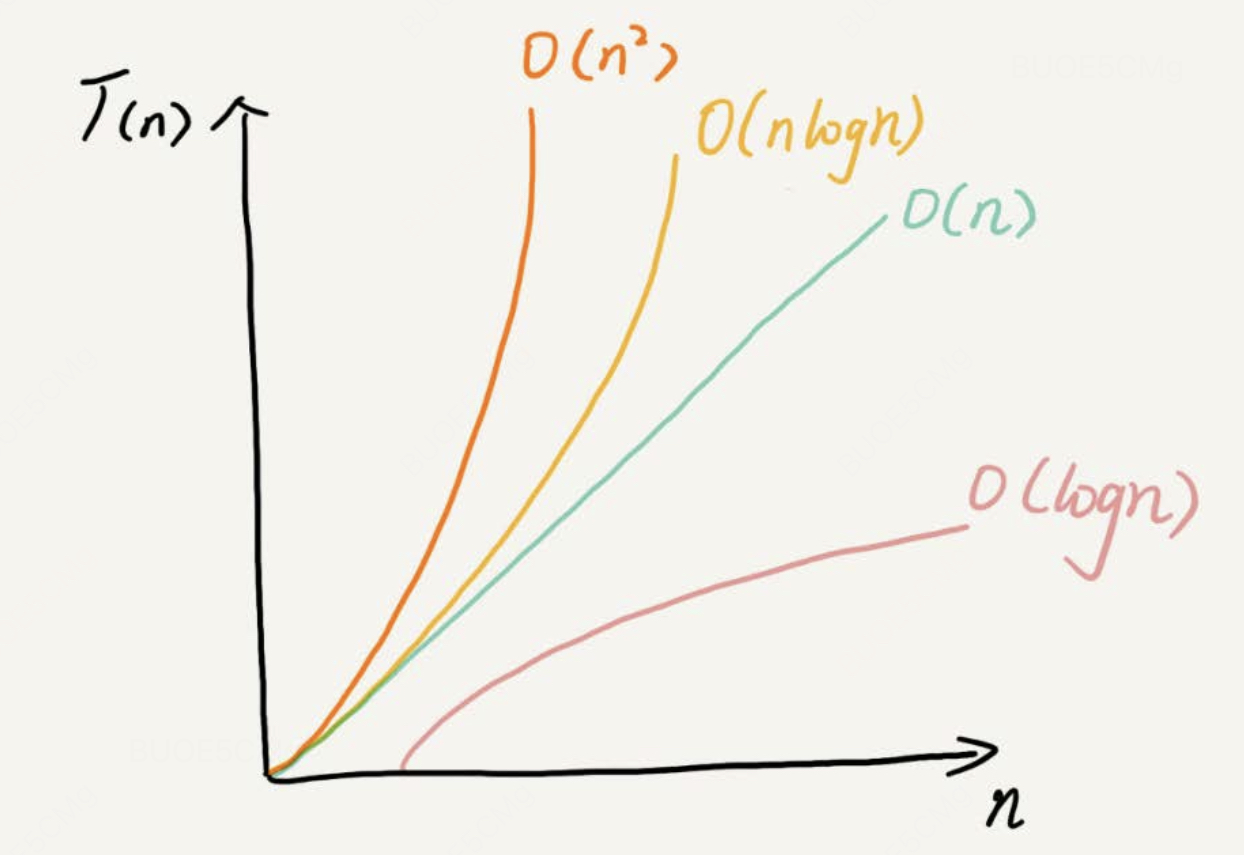
常见的时间复杂度量级
- 多项式量级:下图左侧;
- 非多项式量级:下图右侧波浪线。执行时间会随着数据规模的增大而急剧增大,是非常低效的算法!

空间复杂度
又称为渐进空间复杂度,表示算法的存储空间与数据规模之间的增长关系!
举个栗子🌰,空间复杂度为 O ( n ) O(n) O(n)
def f(n: int):a = 2 # 1个空间存储变量,常量b = [] # 从下面代码可以看出时一个大小为n的数组for i in range(n):b.append(i)return b
参考资料
- 《数据结构与算法之美》王争
相关文章:

算法时空复杂度分析:大O表示法
文章目录 前言大O表示法3个时间复杂度分析原则常见的时间复杂度量级空间复杂度参考资料 前言 算法题写完以后,面试官经常会追问一下你这个算法的时空复杂度是多少?(好像作为一名算法工程师,我日常码代码的过程中,并没…...

threejs简单创建一个几何体(一)
1.下包引入 //下包 npm install three yarn add three//引入 import * as THREE from three2.创建场景,摄像机 // 1.创建场景const scene new THREE.Scene()// 2.创建摄像机//第一个参数是视角,一般在60-90之间,第二个参数是场景的尺寸,一般取显示器的宽高,第三个参数是开始位…...
msfconsole数据库连接不了的问题【已解决】
msfconsole数据库连接 1.msf数据库端口 msf使用的是postgresql,这个数据库默认端口是5432 单个模块的使用可以不需要数据库,但是模块与模块之间需要沟通的时候就会用到数据库。 2.查看msf数据库连接状态 db_status #msf内部查看systemctl status p…...

7. Linux进程环境
进程是操作系统运行程序的一个实例,也是操作系统分配资源的单位。在Linux环境中,每个进程都有独立的进程空间,以便对不同的进程进行隔离,使之不会互相影响。深入理解Linux下的进程环境, 可以帮助我们写出更健壮的代码。 在 Linux 中,进程是程序的一次执行过程,它包含了程…...

[linux] 静态图和动态图
动态图(Dynamic Graphs)和静态图(Static Graphs)通常用来描述深度学习框架中模型的构建方式。 静态图(Static Graphs) 静态图是指模型的计算图在运行前就被定义好并且编译优化的方式。也就是说,…...
1.Spring核心功能梳理
概述 本篇旨在整体的梳理一下Spring的核心功能,让我们对Spring的整体印象更加具体深刻,为接下来的Spring学习打下基础。 本片主体内容如下: Bean的生命周期依赖注入的实现Bean初始化原理推断构造方法原理AOP的实现这里要说明一下,我们这里说到的Spring,一般指的是Spring F…...

活动预告:如何培养高质量应用型医学人才?
在大数据时代与“新医科”建设的背景下,掌握先进的医学数据处理技术成为了医学研究与应用的重要技能。 为了更好地培养社会所需要的高质量应用型医学人才,许多高校已经在广泛地开展面向医学生的医学数据分析教学工作。 在“课-训-赛”育人才系列活动的…...
蓝桥杯算法错题记录-基础篇
文章目录 本文还在跟新,最新跟新时间3/11!!! 格式一定要符合要求,(输入,输出格式)1. nextInt () next() nextLine() 的注意事项2 .数的幂 a^2等3.得到最大长度(最大...&a…...

Java知识点之单例模式
1、单例模式(Binary Search) 单例模式确保某个类只有一个实例,而且自行实例化并向整个系统提供这个实例。在计算机系统中,线程池、缓存、日志对象、对话框、打印机、显卡的驱动程序对象常被设计成单例。这些应用都或多或少具有资…...

Flutter第三弹:常用的Widget
目标: 1)常用的Widget有哪些?有什么特征? 2)开发一个简单的登录页面。 一、Flutter常用Widget 对于Flutter来说,一切皆Widget. 常用的Widget,包括一些基础功能的Widget. 控件名称功能备注…...
Dynamic Wallpaper v17.4 mac版 动态视频壁纸 兼容 M1/M2
Dynamic Wallpaper Engine 是一款适用于 Mac 电脑的视频动态壁纸, 告别单调的静态壁纸,拥抱活泼的动态壁纸。内置在线视频素材库,一键下载应用,也可导入本地视频,同时可以将视频设置为您的电脑屏保。 应用介绍 Dynam…...

Windows / Mac应用程序在Linux系统中的兼容性问题 解决方案
Linux系统可以通过多种方式提高与Windows或Mac应用程序的兼容性。这里有一些解决方案 Windows应用程序兼容性解决方案: Wine Wine是一个允许Linux和Unix系统上运行Windows应用程序的兼容层。 它不是模拟器,而是实现了Windows API的开源实现。 许多W…...
Net Core 使用Mongodb操作文件(上传,下载)
Net Core 使用Mongodb操作文件(上传,下载) 1.Mongodb GridFS 文件操作帮助类。 GridFS 介绍 https://baike.baidu.com/item/GridFS/6342715?fraladdin DLL源码:https://gitee.com/chenjianhua1985/mongodb-client-encapsulati…...
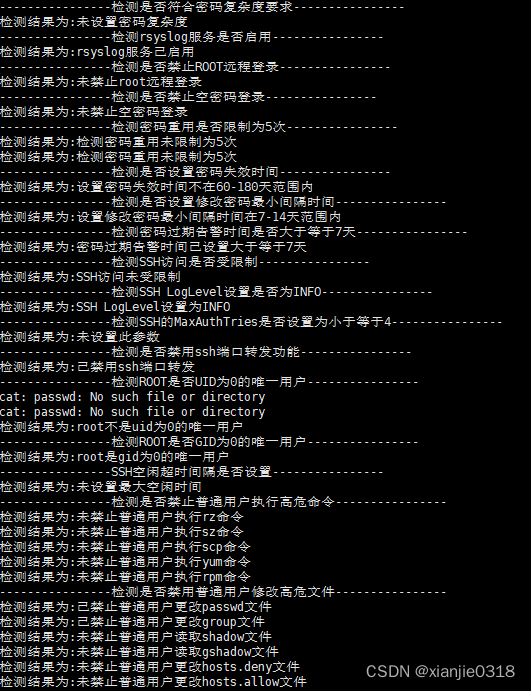
适用于系统版本:CentOS 6/7/8的基线安全检测脚本
#!/bin/bash #适用于系统版本:CentOS 6/7/8 echo "----------------检测是否符合密码复杂度要求----------------" #把minlen(密码最小长度)设置为8-32位,把minclass(至少包含小写字母、大写字母、数字、特殊…...
Seata源码流程图
1.第一阶段分支事务的注册 流程图地址:https://www.processon.com/view/link/6108de4be401fd6714ba761d 2.第一阶段开启全局事务 流程图地址:https://www.processon.com/view/link/6108de13e0b34d3e35b8e4ef 3.第二阶段全局事务的提交 流程图地址…...
英飞凌电源管理PMIC的安全应用
摘要 本篇文档主要用来介绍英飞凌电源管理芯片TLF35584的使用,基于电动助力转向应用来介绍。包含一些安全机制的执行。 TLF35584介绍 TLF35584是英飞凌推出的针对车辆安全应用的电源管理芯片,符合ASIL D安全等级要求,具有高效多电源输出通道&…...

快速在Linux系统安装MySQL
虚拟机使用docker安装MySQL 使用docker拉去镜像 查看mysql的镜像 docker search mysql拉去mysql镜像 docker pull mysql查看下载的镜像 docker images启动容器 docker start mysql进入MySQL容器 docker exec -it mysql /bin/bash登录mysql mysql -u root -p检查是否进入…...
)
数据库相关理论知识(有目录便于直接锁定相关知识点+期末复习)
一,数据模型,关系型数据模型,网状模型,层次模型 1.数据库模型是用来描述和表示现实世界中的事物、概念以及它们之间的关系的工具,但是并不是越专业越好,还要平衡它的模型的复杂性、通用性和成本效益等因素…...

NCC环境配置
一、后端配置 1.安装eclipse汉化插件 2.安装svn插件...

用python实现Dubins曲线生成
Dubins曲线是连接两个具有指定方向和位置的点的最短路径,其中路径受到固定曲率约束(如车辆的转向限制)。Dubins曲线常用于机器人路径规划、车辆轨迹规划等领域。 Dubins曲线可以分为三种类型:CCC (Curve-Curve-Curve), CCL (Curv…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...

Selenium 查找页面元素的方式
Selenium 查找页面元素的方式 Selenium 提供了多种方法来查找网页中的元素,以下是主要的定位方式: 基本定位方式 通过ID定位 driver.find_element(By.ID, "element_id")通过Name定位 driver.find_element(By.NAME, "element_name"…...
OPENCV图形计算面积、弧长API讲解(1)
一.OPENCV图形面积、弧长计算的API介绍 之前我们已经把图形轮廓的检测、画框等功能讲解了一遍。那今天我们主要结合轮廓检测的API去计算图形的面积,这些面积可以是矩形、圆形等等。图形面积计算和弧长计算常用于车辆识别、桥梁识别等重要功能,常用的API…...

【Qt】控件 QWidget
控件 QWidget 一. 控件概述二. QWidget 的核心属性可用状态:enabled几何:geometrywindows frame 窗口框架的影响 窗口标题:windowTitle窗口图标:windowIconqrc 机制 窗口不透明度:windowOpacity光标:cursor…...
