【DL经典回顾】激活函数大汇总(八)(Maxout Softmin附代码和详细公式)
激活函数大汇总(八)(Maxout & Softmin附代码和详细公式)
更多激活函数见激活函数大汇总列表
一、引言
欢迎来到我们深入探索神经网络核心组成部分——激活函数的系列博客。在人工智能的世界里,激活函数扮演着不可或缺的角色,它们决定着神经元的输出,并且影响着网络的学习能力与表现力。鉴于激活函数的重要性和多样性,我们将通过几篇文章的形式,本篇详细介绍两种激活函数,旨在帮助读者深入了解各种激活函数的特点、应用场景及其对模型性能的影响。
在接下来的文章中,我们将逐一探讨各种激活函数,从经典到最新的研究成果。
限于笔者水平,对于本博客存在的纰漏和错误,欢迎大家留言指正,我将不断更新。
二、Maxout
Maxout激活函数是由Ian Goodfellow等人在2013年提出的,旨在通过学习激活函数本身来改进模型性能,特别是在深度学习领域。Maxout激活函数可以被看作是ReLU和其它线性变体激活函数的一般化,具有优秀的模型适应性和表现力。
1. 数学定义
Maxout函数实际上是一个片段线性函数,它的计算过程可以看作是对输入的一组线性变换的最大值。给定一个输入向量 x ∈ R d x \in \mathbb{R}^d x∈Rd和一组权重 W ∈ R m × d W \in \mathbb{R}^{m \times d} W∈Rm×d以及偏置 b ∈ R m b \in \mathbb{R}^m b∈Rm,Maxout激活函数的输出为:
Maxout ( x ) = max i ∈ [ 1 , k ] ( W i ⋅ x + b i ) \operatorname{Maxout}(x)=\max _{i \in[1, k]}\left(W_i \cdot x+b_i\right) Maxout(x)=i∈[1,k]max(Wi⋅x+bi)
这里, W i W_i Wi是权重矩阵的第 i i i行, b i b_i bi是偏置向量的第 i i i个元素, k k k是一组内的单位数,通常作为超参数进行选择。
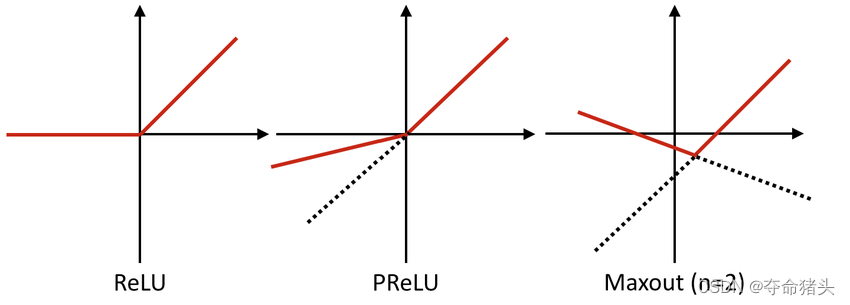
2. 函数特性
- 适应性:Maxout函数可以适应数据和任务,因为它通过学习输入的不同线性组合来形成激活函数本身,提供了极大的灵活性。
- 非饱和性:与ReLU一样,Maxout函数在一定程度上也不容易饱和,这有助于减轻梯度消失问题。
- 兼容性:Maxout可以被看作是包括ReLU、Leaky ReLU在内的多种激活函数的泛化,因此它在理论上可以复制这些激活函数的性能。
3. 导数
Maxout函数的导数取决于在前向传播过程中选择的是哪个线性组合,对于每个输入 x x x,只有使得 W i ⋅ x + b i W_i \cdot x + b_i Wi⋅x+bi最大的那个 i i i对应的权重和偏置会对梯度更新有贡献:
∂ Maxout ( x ) ∂ x = W i ∗ \frac{\partial \operatorname{Maxout}(x)}{\partial x}=W_{i^*} ∂x∂Maxout(x)=Wi∗
其中, i ∗ i^* i∗是使得 W i ⋅ x + b i W_i \cdot x+b_i Wi⋅x+bi达到最大的索引。
4. 使用场景与局限性
使用场景:
- 提高模型表现力:在需要模型具备高度非线性和适应性的任务中,如复杂的分类和回归问题。
- 深度学习模型:Maxout被广泛用于深度网络结构中,特别是在卷积神经网络和全连接层中。
局限性:
- 参数增加:Maxout激活函数需要学习更多的参数(由于需要对每个单元学习多个权重向量和偏置),这可能会导致模型参数显著增加,从而增加过拟合的风险。
- 计算资源需求:与简单的激活函数如ReLU相比,Maxout在计算上更为复杂和资源密集,特别是在处理大规模数据集时。
5.代码实现
实现Maxout激活函数在Python中通常涉及到对输入进行多个线性变换,并取这些变换的最大值。这里,我将展示一个简化的Maxout函数实现,它接受预先计算好的一组线性变换结果作为输入,然后返回每个样本的最大激活值。这个简化版本假设你已经有了一组线性变换的结果,例如,通过多个全连接层(每层对应一个不同的权重集和偏置)处理同一个输入得到的。
import numpy as npdef maxout(inputs):"""简化版的Maxout激活函数。参数:inputs -- 输入值,假定为一个形状为(batch_size, num_units, num_pieces)的三维数组,其中batch_size是批处理大小,num_units是每个Maxout单元的数量,num_pieces是每个单元中线性变换的数量。返回:Maxout激活后的结果,形状为(batch_size, num_units)的二维数组。"""return np.max(inputs, axis=2)
解读
- 输入形状:
inputs应该是一个三维数组,其中第一维是批处理大小(即一次处理多少样本),第二维是Maxout单元的数量,第三维是每个Maxout单元中进行的线性变换的数量。每个Maxout单元对应的是同一个输入通过不同的权重和偏置进行线性变换的结果。 - 最大值操作:
np.max(inputs, axis=2)计算每个Maxout单元中所有线性变换结果的最大值。这里,axis=2指定了沿着第三个维度(即每个单元中不同线性变换的结果)进行最大值操作。 - 输出:函数返回一个二维数组,形状为
(batch_size, num_units),表示每个样本在每个Maxout单元上的最大激活值。
示例使用
以下是如何使用定义的maxout函数来处理一组输入:
# 假设有一个批次包含2个样本,每个样本需要计算2个Maxout单元,每个单元有3个线性变换的结果
inputs = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
maxout_values = maxout(inputs)print("Maxout Values:\n", maxout_values)
例子中,inputs模拟了两个样本通过两个Maxout单元(每个单元有三个线性变换)的处理结果。maxout函数计算并返回每个单元中最大的激活值。
三、Softmin
Softmin激活函数是Softmax函数的一个变体,主要用于多类分类问题中。与Softmax函数将输入向量的元素转换为对应的概率分布不同,Softmin函数关注于将输入向量转换为一个概率分布,其中较小的输入值获得较大的概率。这使得Softmin函数在某些特定的应用场景下,如需要强调较小值的情况,变得非常有用。
1. 数学定义
对于一个输入向量 x ∈ R n x \in \mathbb{R}^n x∈Rn,Softmin函数的输出是一个同样长度的向量,其第 i i i个元素定义为:
Softmin i ( x ) = e − x i ∑ j = 1 n e − x j \operatorname{Softmin}_i(x)=\frac{e^{-x_i}}{\sum_{j=1}^n e^{-x_j}} Softmini(x)=∑j=1ne−xje−xi
这里, x i x_i xi是输入向量中的第 i i i个元素,分母是所有输入元素的指数的和的负值的指数。
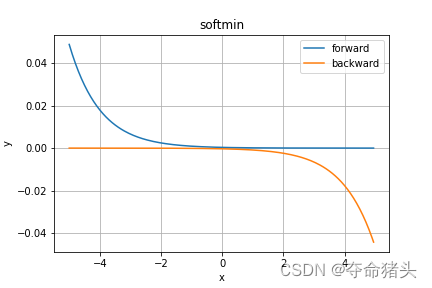
2. 函数特性
- 输出为概率分布:Softmin函数的输出是一个概率分布,其中每个元素的值介于0和1之间,且所有元素的和为1。
- 强调最小值:与Softmax强调最大值不同,Softmin函数通过将较小的输入值转换为较大的输出概率,强调了输入向量中的最小值。
- 平滑性:Softmin函数是平滑且连续的,这对于基于梯度的优化算法非常重要。
3. 导数
Softmin函数的导数相对复杂,对于输入向量 x x x中的第 i i i个元素,其导数可以表示为:
∂ Softmin i ( x ) ∂ x i = − Softmin i ( x ) ( 1 − Softmin i ( x ) ) \frac{\partial \operatorname{Softmin}_i(x)}{\partial x_i}=-\operatorname{Softmin}_i(x)\left(1-\operatorname{Softmin}_i(x)\right) ∂xi∂Softmini(x)=−Softmini(x)(1−Softmini(x))
这表明Softmin函数的导数依赖于函数自身的输出值。
4. 使用场景与局限性
使用场景:
- 多类分类的概率建模:在需要强调较小输入值的多类分类问题中,例如,在某些类型的异常检测或者成本敏感任务中,Softmin可以作为一个有效的选择。
- 配合Softmax使用:在某些情况下,Softmin可以与Softmax一起使用,以提供对输入向量中最大值和最小值的双重关注。
局限性:
- 数值稳定性:和Softmax类似,Softmin在处理具有极大或极小值的输入时可能遇到数值稳定性问题。
- 特定应用场景:Softmin的应用相比Softmax更加特定,不适用于所有类型的多类分类问题。
5.代码实现
可以使用NumPy库计算Softmin函数将每个输入元素的负指数与所有元素负指数的和的倒数相乘,从而计算出每个元素对应的概率值。
import numpy as npdef softmin(x):"""计算Softmin激活函数的值。参数:x -- 输入值,可以是一个数值、一维数组(向量)或二维数组(矩阵)。返回:Softmin激活后的结果。"""e_neg_x = np.exp(-x)return e_neg_x / np.sum(e_neg_x, axis=-1, keepdims=True)
解读
- 计算负指数:
np.exp(-x)计算输入x的每个元素的负指数。这个操作是Softmin函数的核心,因为它将输入向量转换为一个更容易处理的形式,特别是在强调较小输入值时。 - 归一化:通过
np.sum(e_neg_x, axis=-1, keepdims=True)计算所有元素负指数的和,并保持原数组的维度,以便于进行广播操作。然后,将每个元素的负指数与这个和的倒数相乘,从而得到Softmin的输出。 - 支持多维数组:通过指定
axis=-1和keepdims=True,这个实现可以支持对一维或多维数组(如批量处理时的二维数组)进行Softmin计算,使其在深度学习模型中应用更为灵活。
示例使用
以下是如何使用softmin函数来计算一组输入值的Softmin激活:
x = np.array([1.0, 2.0, 3.0, 4.0])
softmin_values = softmin(x)print("Softmin Values:", softmin_values)
这段代码计算了数组x的Softmin激活值。
四、参考文献
Maxout
- Goodfellow, I. J., Warde-Farley, D., Mirza, M., Courville, A., & Bengio, Y. (2013). “Maxout Networks.” In Proceedings of the 30th International Conference on Machine Learning (ICML-13), pp. 1319-1327. 这篇文章首次提出了Maxout网络,详细讨论了其设计原理、优点和在多个基准数据集上的性能。
Softmin
直接关于Softmin激活函数的专门文献可能不如Softmax丰富,因为Softmin通常被视为Softmax的补充或在特定情况下的替代。然而,Softmin的概念和应用可以在涉及Softmax函数以及深度学习模型中概率输出处理的更广泛讨论中找到:
- Bishop, C. M. (2006). “Pattern Recognition and Machine Learning.” Springer. 虽然这本书没有专门讨论Softmin函数,但它提供了关于Softmax函数及其在多类分类问题中应用的深入分析,从而间接地为理解Softmin提供了背景知识。
相关文章:

【DL经典回顾】激活函数大汇总(八)(Maxout Softmin附代码和详细公式)
激活函数大汇总(八)(Maxout & Softmin附代码和详细公式) 更多激活函数见激活函数大汇总列表 一、引言 欢迎来到我们深入探索神经网络核心组成部分——激活函数的系列博客。在人工智能的世界里,激活函数扮演着不…...

Docker进阶:深入了解 Dockerfile
Docker进阶:深入了解 Dockerfile 一、Dockerfile 概述二、Dockerfile 优点三、Dockerfile 编写规则四、Dockerfile 中常用的指令1、FROM2、LABEL3、RUN4、CMD5、ENTRYPOINT6、COPY7、ADD8、WORKDIR9、 ENV10、EXPOSE11、VOLUME12、USER13、注释14、ONBUILD 命令15、…...
【LeetCode热题100】206. 反转链表(链表)
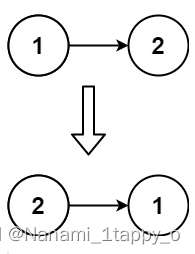
一.题目要求 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。 二.题目难度 简单 三.输入样例 示例 1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 示例 2: 输入:head [1,2…...

电玩城游戏大厅计时软件怎么用,佳易王计时计费管理系统软件定时语音提醒操作教程
电玩城游戏大厅计时软件怎么用,佳易王计时计费管理系统软件定时语音提醒操作教程 一、前言 以下软件操作教程以 佳易王电玩计时计费软件V18.0为例 说明 软件文件下载可以点击最下方官网卡片——软件下载——试用版软件下载 1、软件计时计费,只需点击开…...

selenium也能过某数、5s盾..
文章转载于:selenium也能过某数、5s盾… 直接安装: pip install undetected_chromedriver运行代码: import undetected_chromedriver as uc import timedriver uc.Chrome(executable_pathrC:\Users\chromedriver.exe,version_main111) driver.get(网…...

mysql笔记:8. 视图
文章目录 创建视图修改视图删除视图通过视图更新数据1. 插入数据2. 更新数据3. 删除数据 查看视图信息1. DESCRIBE2. SHOW TABLE STATUS3. SHOW CREATE VIEW4. 在views表中查看 数据库中的视图是一个虚拟表。同真实的表一样,视图包含一系列带有名称的列和行数据。行…...

指针的基本概念和用法
指针的基本概念 每个变量都被存放在从某个内存地址(以字节为单位)开始的若干字节中 “指针”也被称作“指针变量”,大小为4个字节(在64位编译器中,也优肯为8个字节)的变量,其内容代表一个内存地…...

工作随记:oracle重建一张1T数据量的大表
文章目录 一、删除测试表二、重命名旧表:三、验证:四、检查alert日志和昨天到今天的统计信息任务收集是否正常 一、删除测试表 #xshell登录用户hthis用户连接登录处理: sqlplus ht/"123456" sqlplus ht/"123456"10.8.5.…...

使用timm库的一些知识点
timm(Torch Image Models)是一个在PyTorch上构建的图像模型库,它提供了一系列预训练的深度学习模型,使得研究人员和开发者可以方便地进行图像分类、目标检测等任务。 使用timm库创建模型时,如何确定模型的名字 使用…...

一种基于宏和serde_json实现的rust web中统一返回类
本人rust萌新,写web碰到了这个,基于ChatGPT和文心一言学了宏,强行把这玩意实现出来了,做个学习记录,如果有更好的方法,勿喷。 先看效果,注意不支持嵌套,且kv映射要用>(因为它这个…...
每周一算法:A*(A Star)算法
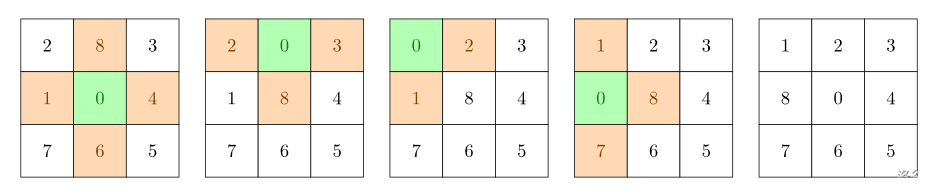
八数码难题 题目描述 在 3 3 3\times 3 33 的棋盘上,摆有八个棋子,每个棋子上标有 1 1 1 至 8 8 8 的某一数字。棋盘中留有一个空格,空格用 0 0 0 来表示。空格周围的棋子可以移到空格中。要求解的问题是:给出一种初始布局…...
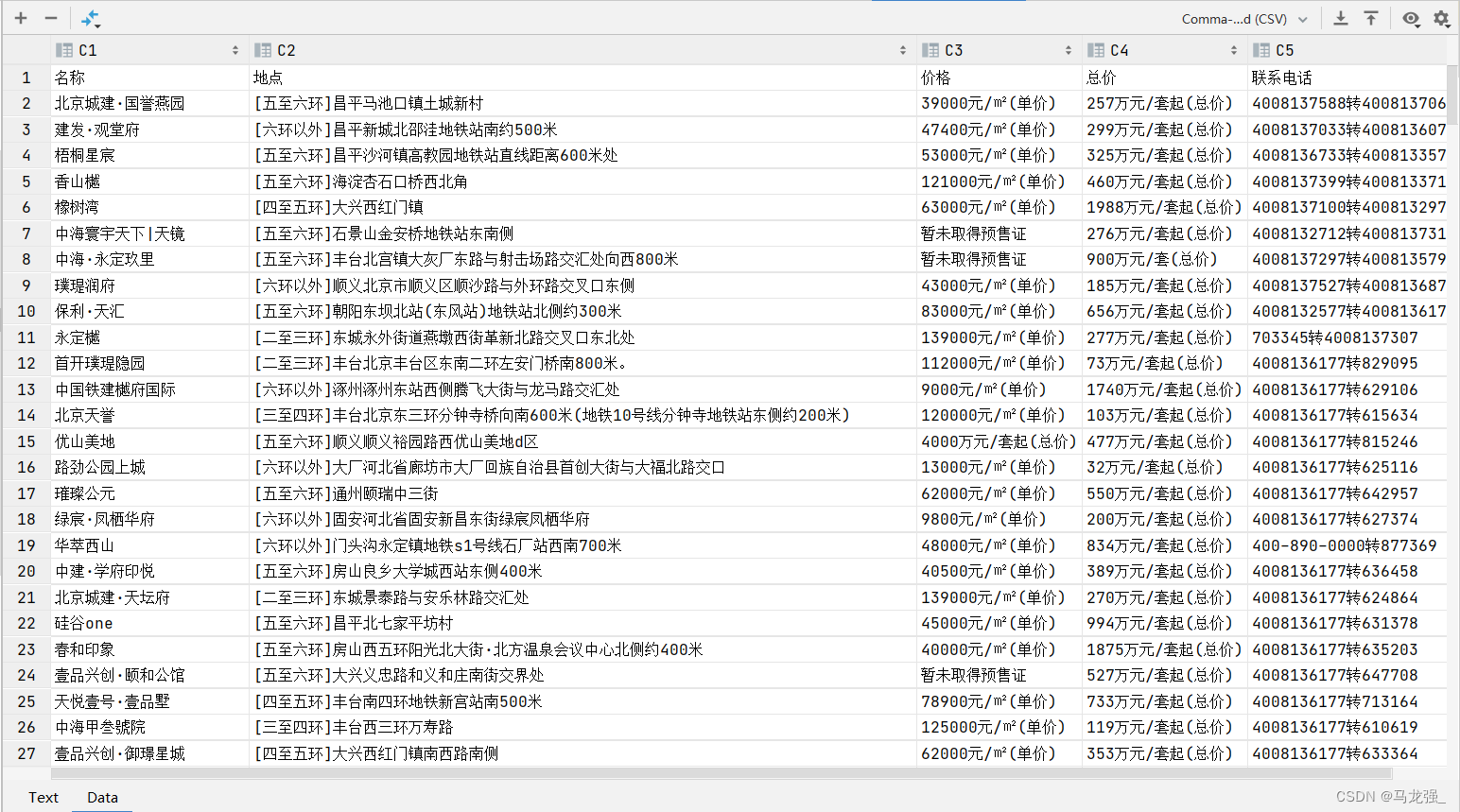
爬虫练习:获取某网站的房价信息
一、相关网站 二、相关代码 import requests from lxml import etree import csv with open(房天下数据.csv, w, newline, encodingutf-8) as csvfile:fieldnames [名称, 地点,价格,总价,联系电话]writer csv.DictWriter(csvfile, fieldnamesfieldnames)writer.writeheader…...

第一个C语言hello world
#include <stdio.h> int main() {printf("hello world ! \n");//打印函数return 0; } "#" : 预处理标志 include <> : 表示预处理的文件在<>内 stdio.h : 标准的io头文件 // io : 输入输出 // printf()…...

【Python】新手入门学习:详细介绍依赖倒置原则(DIP)及其作用、代码示例
【Python】新手入门学习:详细介绍依赖倒置原则(DIP)及其作用、代码示例 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、Py…...
)
嵌入式驱动学习目录索引(更新中)
前言 这是一篇索引博客,用来作为索引记录学习嵌入式Linux的过程,可以用来给自己以及需要的读者作为一个目录索引,每次更新完博客都会添加进该目录中。 嵌入式驱动学习专栏将详细记录博主学习驱动的详细过程,未来预计四个月将高强度…...
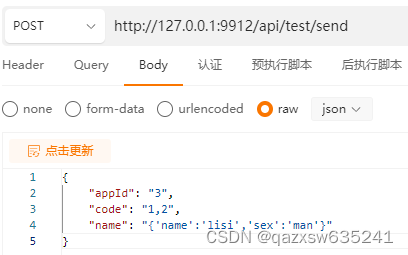
ruoyi-vue插件集成websocket
链接:插件集成 | RuoYi WebSocketServer.java:补充代码 /*** 此为广播消息* param message 消息内容*/public void sendAllMessage(String message) {LOGGER.info("【websocket.sendAllMessage】广播消息:"message);try {for(String sessionI…...
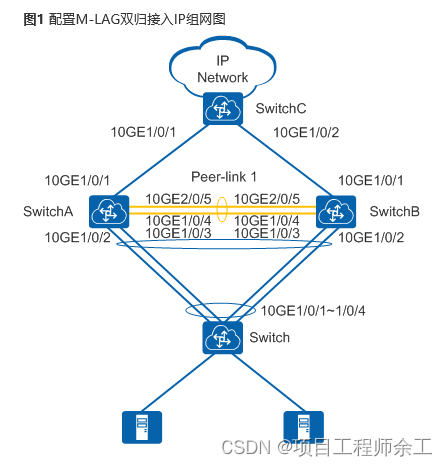
华为ce12800交换机m-lag(V-STP模式)配置举例
配置## 标题思路 采用如下的思路配置M-LAG双归接入IP网络: 1.在Switch上配置上行接口绑定在一个Eth-Trunk中。 2.分别在SwitchA和SwitchB上配置V-STP、DFS Group、peer-link和M-LAG接口。 3.分别在SwitchA和SwitchB上配置LACP M-LAG的系统优先级、系统ID。 4.分别在…...
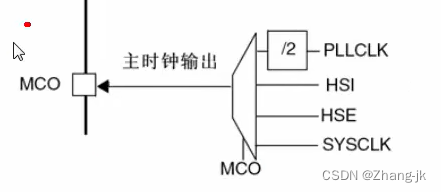
STM32第九节(中级篇):RCC——时钟树讲解(第一节)
目录 前言 STM32第九节(中级篇):RCC——时钟树讲解 时钟树主系统时钟讲解 HSE时钟 HSI时钟 锁相环时钟 系统时钟 SW位控制 HCLK时钟 PCLKI时钟 PCLK2时钟 RTC时钟 MCO时钟输出 6.2.7时钟安全系统(CSS) 小结 前言 从…...

c/c++字符串处理标准库 string 介绍
c语言中string.h介绍 C语言的标准库中包含了一个头文件 <string.h>,该头文件提供了一系列字符串处理函数的声明和定义。以下是一些常用的函数: 字符串复制:strcpy(dest, src)。将源字符串 src 复制到目标字符串 dest,包括…...

HarmonyOS NEXT应用开发之深色模式适配
介绍 本示例介绍在开发应用以适应深色模式时,对于深色和浅色模式的适配方案,采取了多种策略如下: 固定属性适配:对于部分组件的颜色属性,如背景色或字体颜色,若保持不变,可直接设定固定色值或…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
