每周一算法:A*(A Star)算法
八数码难题
题目描述
在 3 × 3 3\times 3 3×3 的棋盘上,摆有八个棋子,每个棋子上标有 1 1 1 至 8 8 8 的某一数字。棋盘中留有一个空格,空格用 0 0 0 来表示。空格周围的棋子可以移到空格中。要求解的问题是:给出一种初始布局(初始状态)和目标布局(为了使题目简单,设目标状态为 123804765 123804765 123804765),找到一种最少步骤的移动方法,实现从初始布局到目标布局的转变。
输入格式
输入初始状态,一行九个数字,空格用 0 0 0 表示。
输出格式
只有一行,该行只有一个数字,表示从初始状态到目标状态需要的最少移动次数。保证测试数据中无特殊无法到达目标状态数据。
样例 #1
样例输入 #1
283104765
样例输出 #1
4
提示
样例解释
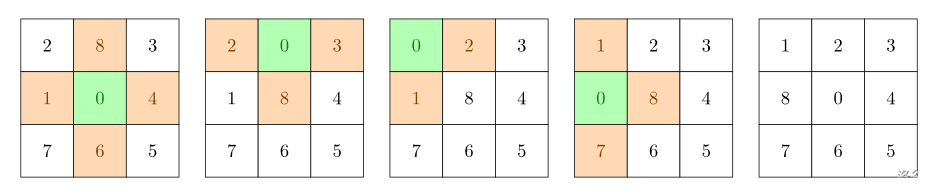
图中标有 0 0 0 的是空格。绿色格子是空格所在位置,橙色格子是下一步可以移动到空格的位置。如图所示,用四步可以达到目标状态。
并且可以证明,不存在更优的策略。
广度优先搜索
算法思想
根据题目描述,输入一个棋盘的初始状态,求从初始状态到目标状态需要的最少移动次数,可以用广度优先搜索求解,基本思想如下:
- 将初始状态 start \text{start} start的移动步数设为 0 0 0,然后将其加入队列
- 只要队列不为空
- 从队首取出一个状态 state \text{state} state
- 如果 state = end \text{state}=\text{end} state=end结束状态,则搜索结束,返回到达的 state \text{state} state移动步数
- 否则,找到 state \text{state} state中字符 0 0 0的位置,向相邻方向进行扩展
- 如果扩展到一个新的状态,则计算扩展到新状态的步数,并将新状态加入队列
代码实现
#include <bits/stdc++.h>
using namespace std;
queue<string> q;
unordered_map<string,int> dis;int dx[]={-1, 1, 0, 0}, dy[]={0, 0, -1, 1};int bfs(string start)
{string end = "123804765";dis[start] = 0;q.push(start);while(!q.empty()){string state = q.front(); q.pop();int step = dis[state];if(state == end) return step;int k = state.find('0'); //在当前状态的字符串中找到字符0int x = k / 3, y = k % 3; //将字符串中的位置转换为矩阵中的坐标for(int i = 0; i < 4; i ++){int a = x + dx[i], b = y + dy[i]; if(a < 0 || a >= 3 || b < 0 || b >= 3) continue; //越界swap(state[k], state[a * 3 + b]); //将数字字符与0进行交换,转移到新状态if(!dis.count(state)) //没有访问过{ dis[state] = step + 1; //转移到state状态的最小步数q.push(state); //入队}swap(state[k], state[a * 3 + b]); //恢复现场,交换回来,为下次转移做准备}}return -1;
}int main()
{string start;char c;for(int i = 0; i < 9; i ++){cin >> c;start += c;}cout << bfs(start) << endl;return 0;
}
A*算法
通过BFS可以发现,对每个状态都可以将 0 0 0向上右下左四个方向进行扩展,在最坏情况下要搜索的状态空间为 4 9 4^9 49,指数级别,搜索的效率比较低。在这种情况下,可以使用A*算法进行求解。
A*(A Star)算法是一种很常用的路径查找和图形遍历算法,它有较好的性能和准确度。
A*算法通过下面的函数来计算每个状态的优先级:
f ( n ) = g ( n ) + h ( n ) f(n)=g(n) + h(n) f(n)=g(n)+h(n)
其中:
- f ( n ) f(n) f(n)是当前状态 n n n的综合优先级。当选择下一个要扩展的状态时,我们总会选取综合优先级最高(值最小)的状态。
- g ( n ) g(n) g(n)是状态距离起点(初始状态)的代价
- h ( n ) h(n) h(n)是状态 n n n距离终点(目标状态)的预计代价,这也就是A*算法的启发函数。
算法思想
A*算法与BFS类似,不同之处在于A*算法使用优先队列,选取 f ( n ) f(n) f(n)值最小(优先级最高)的状态作为下一个待扩展的状态。基本思想如下:
- 将初始状态 start \text{start} start的移动步数设为 0 0 0,然后其综合优先级和初始状态加入优先队列
- 只要队列不为空
- 取出优先队列中综合优先级最高(值最小)的状态 state \text{state} state
- 如果 state = end \text{state}=\text{end} state=end结束状态,则搜索结束,返回到达的 state \text{state} state移动步数
- 否则,找到 state \text{state} state中字符 0 0 0的位置,向相邻方向进行扩展
- 如果扩展到一个新状态,或者到达该状态的步数减少,将状态的综合优先级和状态本身继续加入优先队列
启发函数
从算法的基本思想可以看出来,启发函数会影响A*算法的行为。
- 在极端情况下,当启发函数 h ( n ) h(n) h(n)为0时,则将由 g ( n ) g(n) g(n)决定状态的优先级,此时算法就退化成了Dijkstra算法。
- 如果 h ( n ) h(n) h(n)始终小于等于状态 n n n到终点的代价,则A*算法保证一定能够找到最短路径。但是当 h ( n ) h(n) h(n)的值越小,算法将遍历越多的状态,也就导致算法越慢。
- 如果 h ( n ) h(n) h(n)完全等于状态 n n n到终点的代价,则A*算法将找到最佳路径,并且速度很快。可惜的是,并非所有场景下都能做到这一点。因为在没有达到终点之前,很难确切算出距离终点还有多远。
- 如果 h ( n ) h(n) h(n)的值比状态 n n n到终点的代价要大,则A*算法不能保证找到最短路径,不过此时会很快。
通过调节启发函数我们可以控制算法的速度和精确度。因为在一些情况,可能未必需要最短路径,而是希望能够尽快找到一个路径即可,这也是A*算法比较灵活的地方。
对于网格形式的图,有以下这些启发函数可以使用:
- 如果图形中只允许朝上下左右四个方向移动,则可以使用曼哈顿距离(Manhattan distance)。
- 如果图形中允许朝八个方向移动,则可以使用对角距离。
- 如果图形中允许朝任何方向移动,则可以使用欧几里得距离(Euclidean distance)。
代码实现
#include <iostream>
#include <algorithm>
#include <queue>
#include <unordered_map>
using namespace std;
typedef pair<int, string> PIS;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
//启发函数取当前状态中每个数字与其目标位置的曼哈顿距离之和
int h(string state)
{int res = 0;for(int i = 0; i < state.size(); i ++){if(state[i] != '0'){int t = state[i] - '1';res += abs(i / 3 - t / 3) + abs(i % 3 - t % 3); //累加每个数字到其正确位置的曼哈顿距离}}return res;
}
int astar(string start)
{string end = "123804765";priority_queue<PIS, vector<PIS>, greater<PIS>> heap; //小顶堆unordered_map<string, int> dis; //记录到达每一种状态的步数//g(start)返回起点到终点的预估距离heap.push({0 + h(start), start});dis[start] = 0;while(heap.size()){PIS t = heap.top(); heap.pop();string state = t.second;if(state == end) break; //终点第一次出队,搜索结束int step = dis[state];int k = state.find('0'); //找到0所在位置int x = k / 3, y = k % 3; for(int i = 0; i < 4; i ++){int a = x + dx[i], b = y + dy[i];if(a < 0 || a >= 3 || b < 0 || b >= 3) continue;swap(state[x * 3 + y], state[a * 3 + b]); //将0和目标交换if(!dis.count(state) || dis[state] > step + 1) //如果扩展到一个新的状态,或者能够缩短到state的距离{dis[state] = step + 1;heap.push({dis[state] + h(state), state}); //将综合优先级和状态加入优先队列}swap(state[x * 3 + y], state[a * 3 + b]);//恢复现场}}return dis[end];
}
int main()
{char c;string start;for(int i = 0; i < 9; i ++){cin >> c;start += c;}cout << astar(start);return 0;
}
相关练习
洛谷P2324:骑士精神
相关文章:

每周一算法:A*(A Star)算法
八数码难题 题目描述 在 3 3 3\times 3 33 的棋盘上,摆有八个棋子,每个棋子上标有 1 1 1 至 8 8 8 的某一数字。棋盘中留有一个空格,空格用 0 0 0 来表示。空格周围的棋子可以移到空格中。要求解的问题是:给出一种初始布局…...
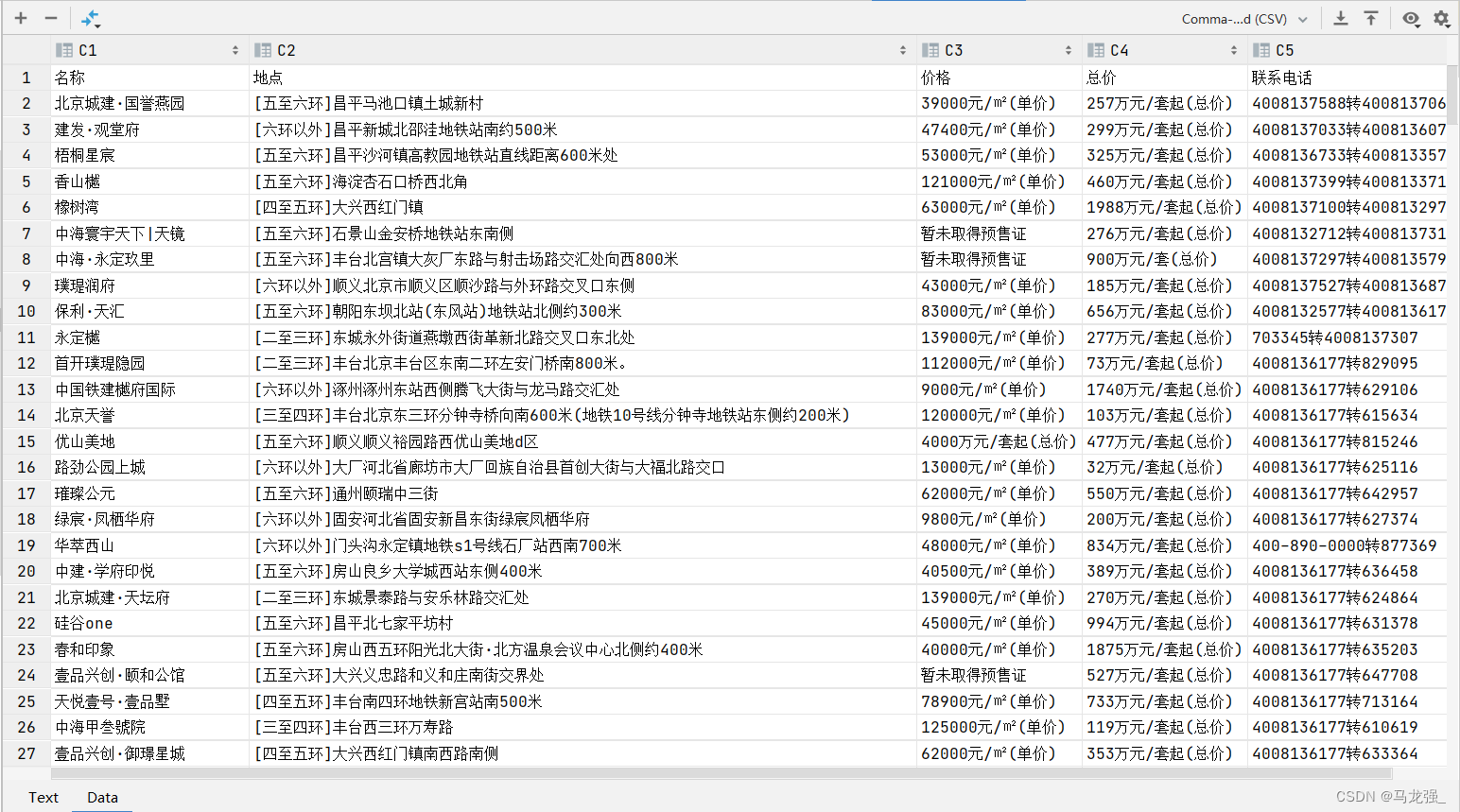
爬虫练习:获取某网站的房价信息
一、相关网站 二、相关代码 import requests from lxml import etree import csv with open(房天下数据.csv, w, newline, encodingutf-8) as csvfile:fieldnames [名称, 地点,价格,总价,联系电话]writer csv.DictWriter(csvfile, fieldnamesfieldnames)writer.writeheader…...

第一个C语言hello world
#include <stdio.h> int main() {printf("hello world ! \n");//打印函数return 0; } "#" : 预处理标志 include <> : 表示预处理的文件在<>内 stdio.h : 标准的io头文件 // io : 输入输出 // printf()…...

【Python】新手入门学习:详细介绍依赖倒置原则(DIP)及其作用、代码示例
【Python】新手入门学习:详细介绍依赖倒置原则(DIP)及其作用、代码示例 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、Py…...
)
嵌入式驱动学习目录索引(更新中)
前言 这是一篇索引博客,用来作为索引记录学习嵌入式Linux的过程,可以用来给自己以及需要的读者作为一个目录索引,每次更新完博客都会添加进该目录中。 嵌入式驱动学习专栏将详细记录博主学习驱动的详细过程,未来预计四个月将高强度…...
ruoyi-vue插件集成websocket
链接:插件集成 | RuoYi WebSocketServer.java:补充代码 /*** 此为广播消息* param message 消息内容*/public void sendAllMessage(String message) {LOGGER.info("【websocket.sendAllMessage】广播消息:"message);try {for(String sessionI…...
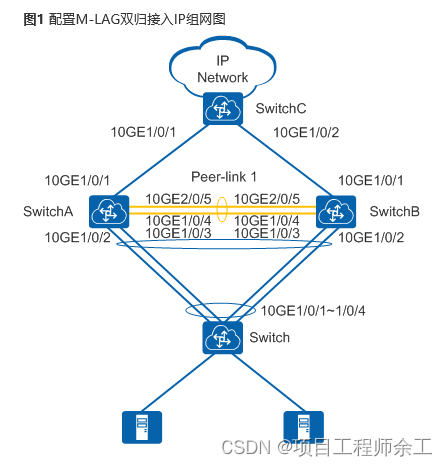
华为ce12800交换机m-lag(V-STP模式)配置举例
配置## 标题思路 采用如下的思路配置M-LAG双归接入IP网络: 1.在Switch上配置上行接口绑定在一个Eth-Trunk中。 2.分别在SwitchA和SwitchB上配置V-STP、DFS Group、peer-link和M-LAG接口。 3.分别在SwitchA和SwitchB上配置LACP M-LAG的系统优先级、系统ID。 4.分别在…...
STM32第九节(中级篇):RCC——时钟树讲解(第一节)
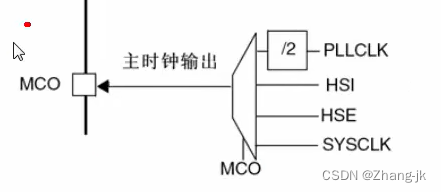
目录 前言 STM32第九节(中级篇):RCC——时钟树讲解 时钟树主系统时钟讲解 HSE时钟 HSI时钟 锁相环时钟 系统时钟 SW位控制 HCLK时钟 PCLKI时钟 PCLK2时钟 RTC时钟 MCO时钟输出 6.2.7时钟安全系统(CSS) 小结 前言 从…...

c/c++字符串处理标准库 string 介绍
c语言中string.h介绍 C语言的标准库中包含了一个头文件 <string.h>,该头文件提供了一系列字符串处理函数的声明和定义。以下是一些常用的函数: 字符串复制:strcpy(dest, src)。将源字符串 src 复制到目标字符串 dest,包括…...

HarmonyOS NEXT应用开发之深色模式适配
介绍 本示例介绍在开发应用以适应深色模式时,对于深色和浅色模式的适配方案,采取了多种策略如下: 固定属性适配:对于部分组件的颜色属性,如背景色或字体颜色,若保持不变,可直接设定固定色值或…...

Go微服务: 基于Go Micro框架实现微服务调用
Go Micro 1 )概述 在具体的项目开发过程中,开发者聚焦的是业务逻辑的开发和功能的实现大量的环境配置,调试搭建等基础性工作会耗费相当一部分的精力因此有必要将微服务架构中所涉及到的,相关的解决方案做集中管理和维护Go Micro …...

大模型prompt提示词如何调优?
当使用大型模型(如GPT-3.5)时,可以通过优化提示(prompt)来引导模型生成更加符合预期的内容。以下是一些调优提示词的建议: 1、清晰的问题陈述:确保你的问题或提示清晰、简明,能够准…...

【Python/crawl】如何使用Python爬虫将一系列网页上的同类图片下载到本地
【需求】 从网页https://www.zhainq.com/%e7%be%8e%e5%a5%b3%e5%86%99%e7%9c%9f%e6%9c%ba%e6%9e%84/%e6%97%a5%e6%9c%ac%e7%be%8e%e5%a5%b3%e5%86%99%e7%9c%9f/109012.html 开始,有十七页,每页都有大漂亮“小濑田麻由”的若干图片,想要将其…...

Postgresql 连接数查看,死锁问题解决
-- 查看所有连接 select * -- datname,pid,application_name,state from pg_stat_activity; -- 查询最大连接数 select max_conn-now_conn as resi_conn from (select setting::int8 as max_conn,(select count(*) from pg_stat_activity) as now_conn from pg_settings where…...

ssm蛋糕甜品商城系统(程序+文档+数据库)
** 🍅点赞收藏关注 → 私信领取本源代码、数据库🍅 本人在Java毕业设计领域有多年的经验,陆续会更新更多优质的Java实战项目,希望你能有所收获,少走一些弯路。🍅关注我不迷路🍅** 一、研究背景…...
算法空间复杂度计算
目录 空间复杂度定义 影响空间复杂度的因素 算法在运行过程中临时占用的存储空间讲解 例子 斐波那契数列递归算法的性能分析 二分法(递归实现)的性能分析 空间复杂度定义 空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大…...

C++ lambda函数个人理解
及方便自己在函数内部定义函数 int main() {int i 1;auto c [](int a, int c) {return ab;};int d a(2, i);cout<<c;return 0; }格式: auto functionname [capture](parameters) -> return_type { /* … */ }; (1)[capture] &a…...

SwiftUI的context Menu
SwiftUI的 context Menu 现在来演示一下如何使用 SwiftUI 的 Context Menu 。 代码: import SwiftUIstruct ContextMenuBootCamp: View {State var bgColor: Color .purplevar body: some View {VStack(alignment: .leading, spacing: 10.0) {Image(systemName: …...
【数据结构】树与堆 (向上/下调整算法和复杂度的分析、堆排序以及topk问题)
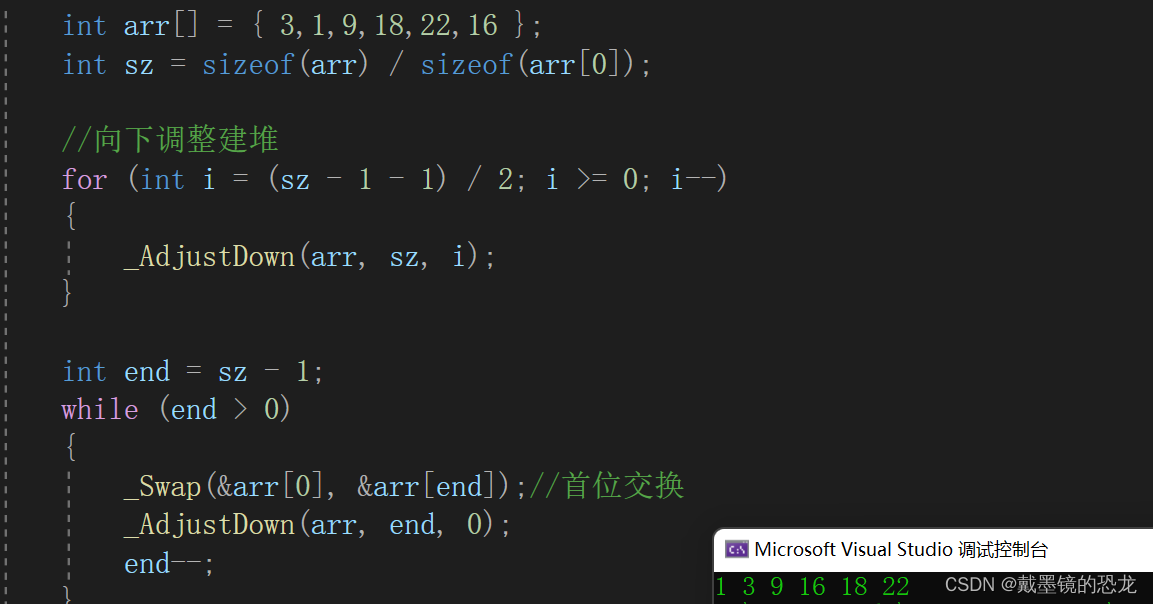
文章目录 1.树的概念1.1树的相关概念1.2树的表示 2.二叉树2.1概念2.2特殊二叉树2.3二叉树的存储 3.堆3.1堆的插入(向上调整)3.2堆的删除(向下调整)3.3堆的创建3.3.1使用向上调整3.3.2使用向下调整3.3.3两种建堆方式的比较 3.4堆排…...

安装CDH平台的服务器磁盘满了,磁盘清理过程记录
1.使用hdfs命令查看哪个文件占用最大 hdfs dfs -du -h /tmp 2.我的服务器上显示/tmp/hive/hive文件夹下的,一串字符串命名的文件特别大几乎把磁盘占满了 网上查到/tmp文件是临时文件,由于hiveserver2任务运行异常导致缓存未删除,正常情况下…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
