【数据结构】树与堆 (向上/下调整算法和复杂度的分析、堆排序以及topk问题)
文章目录
- 1.树的概念
- 1.1树的相关概念
- 1.2树的表示
- 2.二叉树
- 2.1概念
- 2.2特殊二叉树
- 2.3二叉树的存储
- 3.堆
- 3.1堆的插入(向上调整)
- 3.2堆的删除(向下调整)
- 3.3堆的创建
- 3.3.1使用向上调整
- 3.3.2使用向下调整
- 3.3.3两种建堆方式的比较
- 3.4堆排序
- 3.5TopK问题

1.树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。如下图:
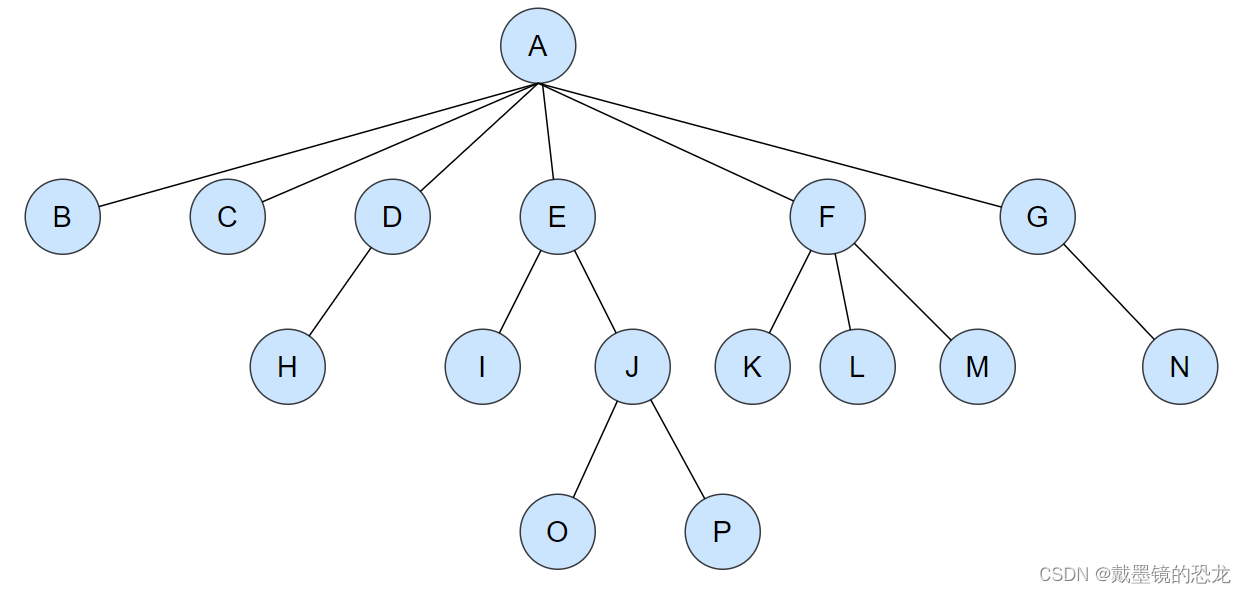
有一个特殊的结点,称为根结点,根节点没有前驱结点。例如A节点
除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。
例如:B节点又可以分成一棵树,该树只有根,没有子树。
D节点可以分为根节点和子树。D为根节点,只有一棵子树H。
因此树可以拆分为:根和子树。 每棵子树的根结点有且只有一个前驱,可以有0个或多个后继;所以,树是递归定义的。
注意:树形结构中,子树之间不能有交集,否则就不是树形结构,即:树中不能有环!。例如:
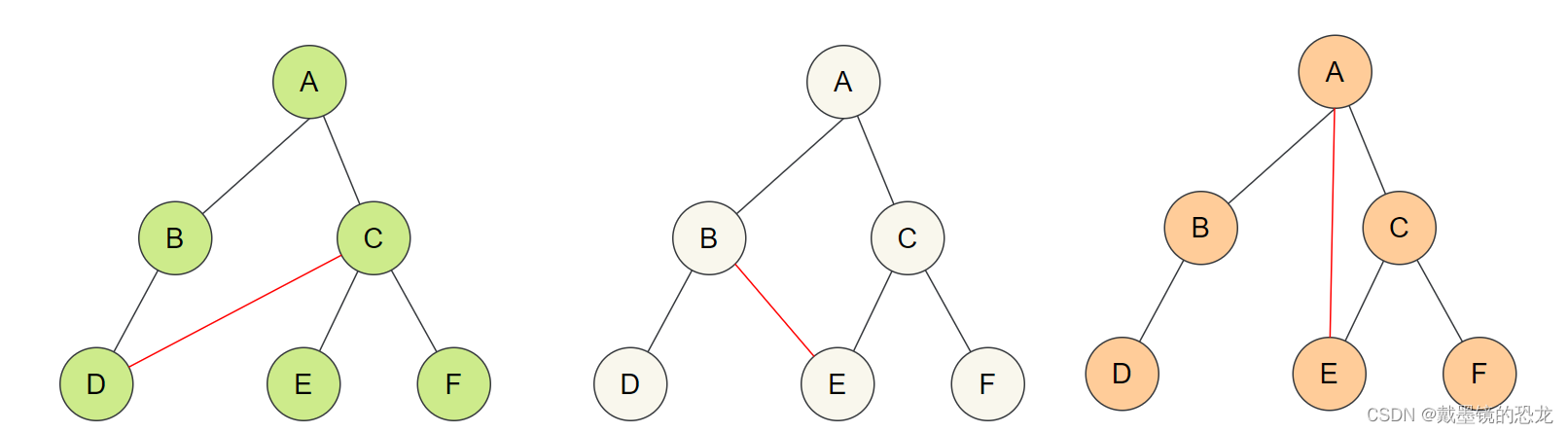

1.1树的相关概念
- 节点的度:一个
节点含有的子树的个数称为该节点的度; 如上图:A的为6 - 叶节点或终端节点:
度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点 - 分支节点或非终端节点:
度不为0的节点; 如上图:D、E、F、G…等节点为分支节点 - 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的
子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点,H是D的孩子节点 - 兄弟节点:具有
相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点 - 树的度:一棵树中,
最大的节点的度称为树的度; 如上图:树的度为6 - 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中
节点的最大层次; 如上图:树的高度为4 - 堂兄弟节点:
双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点 - 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先;P的祖先是A、E、J
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m(m>0)棵互不相交的树的集合称为森林;
1.2树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系。所以树的结构应该怎么定义呢?
//假设树的度为6
#define N 6
struct TreeNode
{int val;struct TreeNode* Child[N];
};
如果这样定义的话,不管你子树有没有孩子都开辟了空间,会比较浪费。
struct TreeNode
{int val;struct TreeNode** Child;//使用顺序表存储孩子int size;//当前个数int capacity;//容量
};
既然浪费了空间,那咱们就动态申请,有几个孩子由size决定,不够就扩容,但这种结构好像也不太好。
struct TreeNode
{int val;struct TreeNode* leftChile;//左孩子struct TreeNode* nextBrother;//右兄弟
};
左孩子右兄弟法:这种方法设计的非常巧妙,每个节点只记录它左边第一个孩子,其它孩子是第一个孩子的兄弟,由第一个孩子记录。这种方法好像看起来是最好的
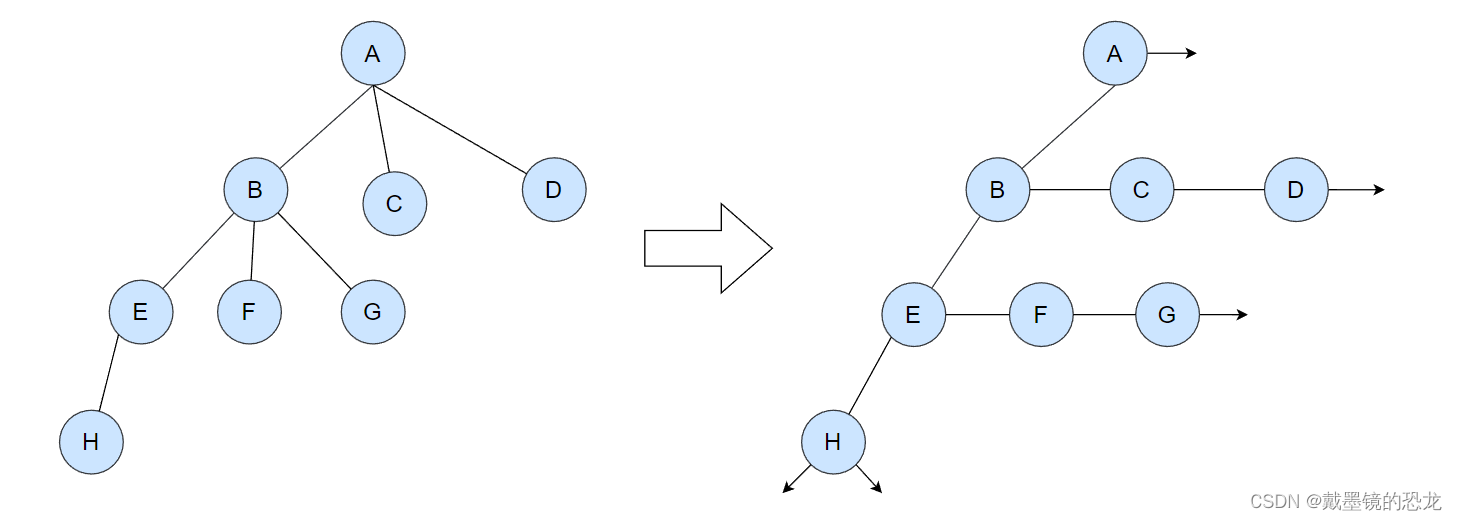
2.二叉树
2.1概念
二叉树是从树衍生出来的。
那什么叫二叉树呢?
二叉树:首先它是一棵树,其次它每个节点最多有两个分支;并且对两个分支进行区分,分别叫做左子树和右子树。如下图
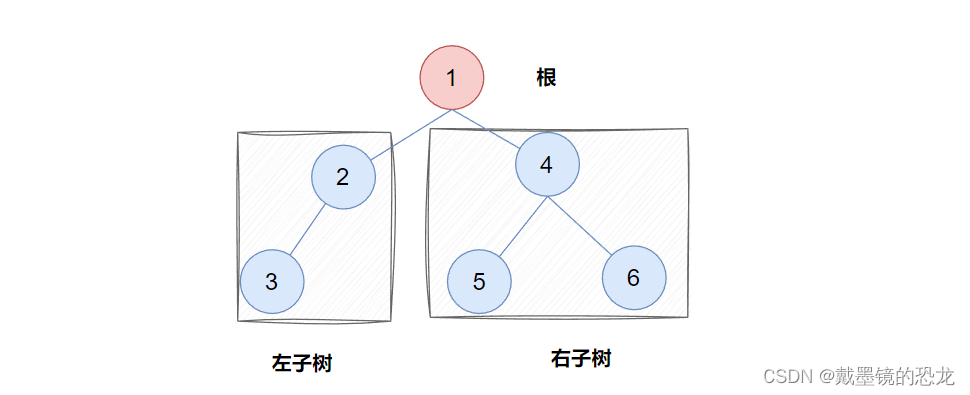
从上图可以看出:
- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:
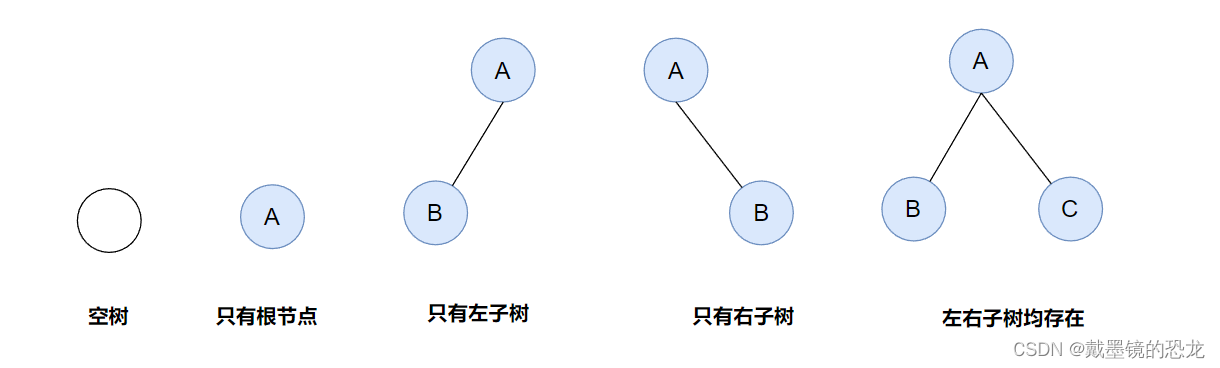
2.2特殊二叉树
- 满二叉树
满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。
满二叉树的前n-1层全是满的(度为2),叶子全在最后一层
如果一个二叉树的层数为K,且结点总数是2k-1,则这个二叉树就是满二叉树。
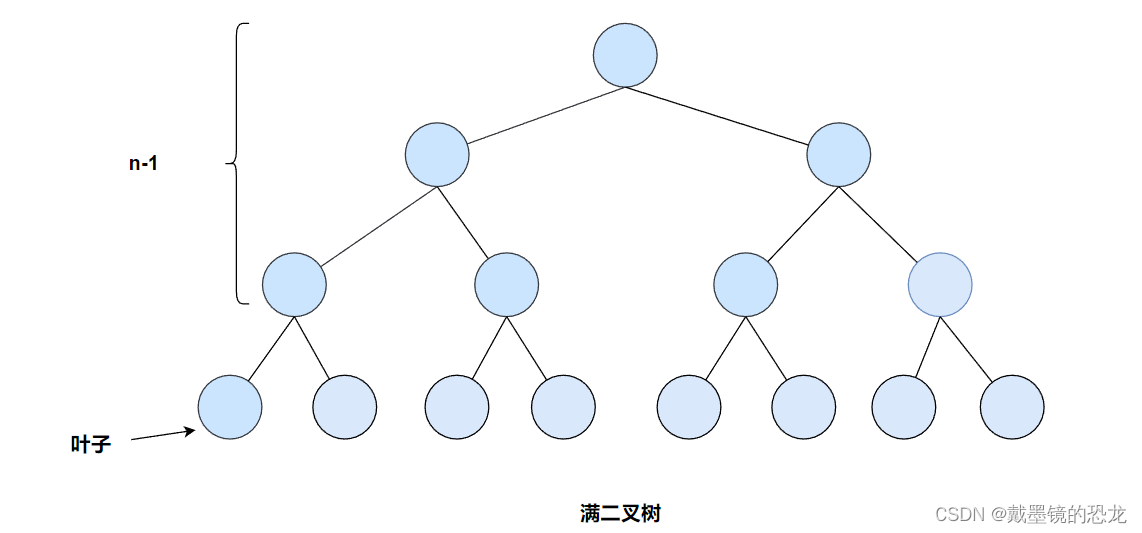
- 完全二叉树
完全二叉树跟满二叉树的区别是:完全二叉树的前n-1层也都是满的,最后一层不一定满,但是要求从左到右的节点连续,不能空。(没有左孩子就不能有右孩子)
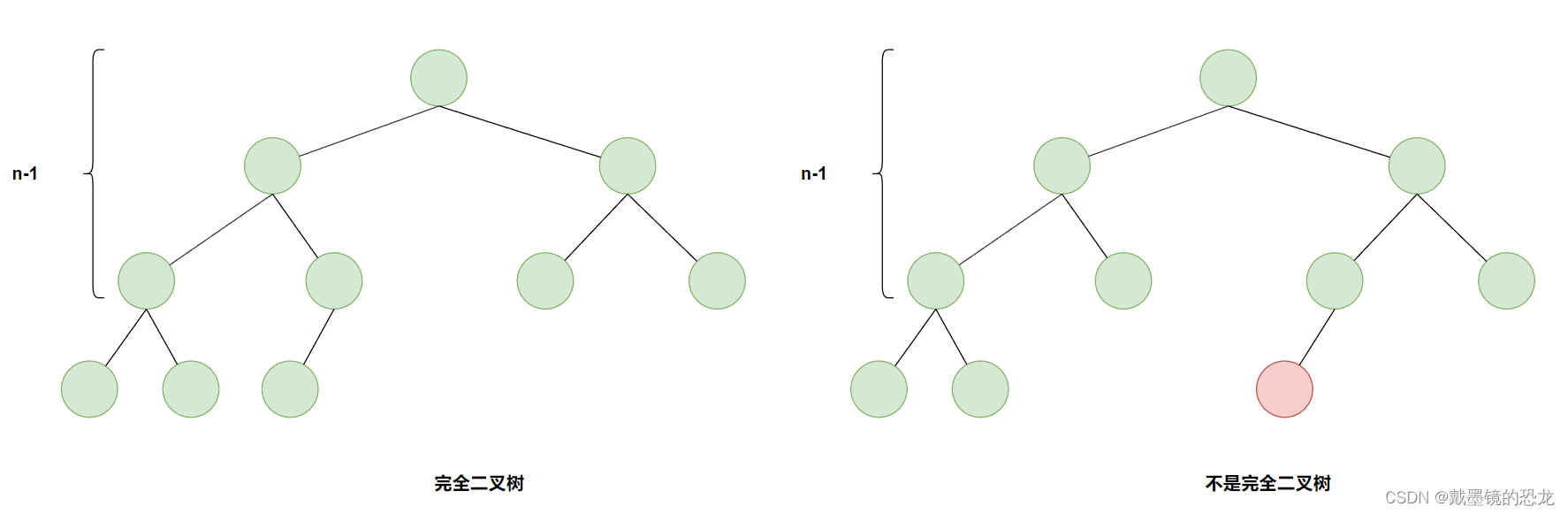
2.3二叉树的存储
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
- 顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树
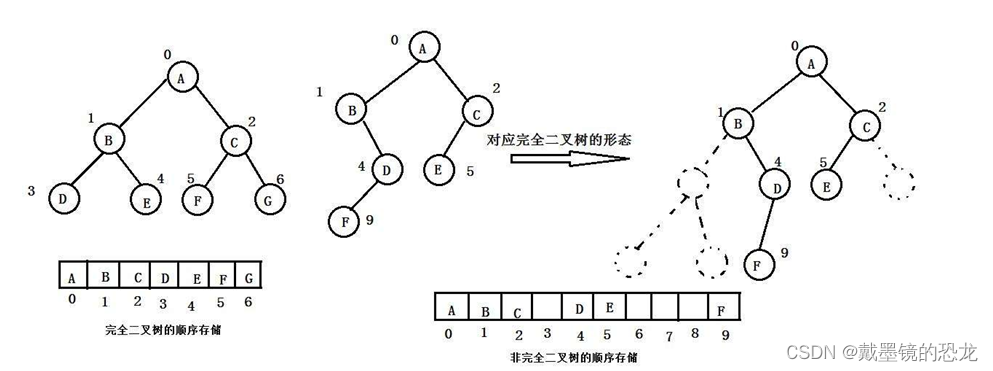
使用顺序存储存在一个规律:
-
leftChild = parent*2+1
- 例:C的左孩子的下标为2 * 2+1 = 5
-
rightChild = parent*2+2
- 例:C的右孩子的下标为2 * 2+2 = 6
-
parent = (Child - 1) / 2
- 例:F的父亲下标为(5-1)/ 2 = 2 G的父亲下标为(6-1)/ 2 = 2
-
有了这个规律我就不需要存储我的孩子或父亲在哪里,我使用下标算就可以了。
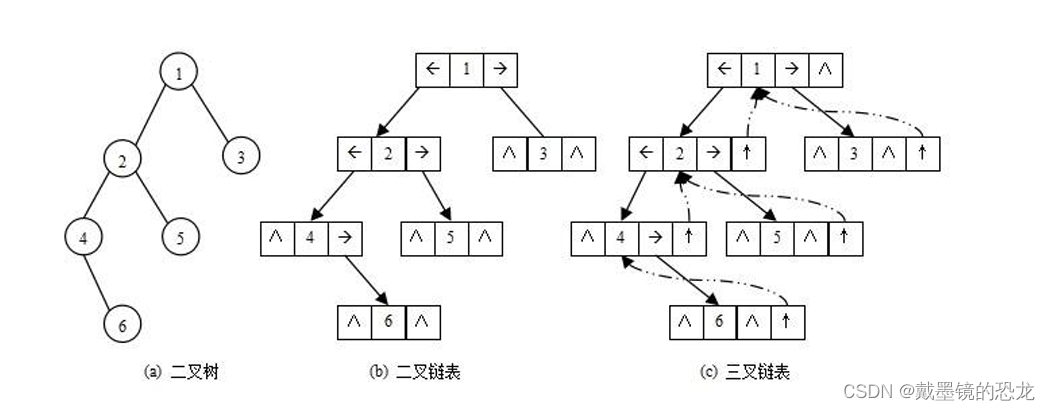
- 链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别 用来给出该结点左孩子和右孩子所在的链结点的存储地址,链式结构又分为二叉链和三叉链, 。
该结构一般用来存储非完全二叉树,不会有空间的浪费。
3.堆
- 普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。
- 完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储
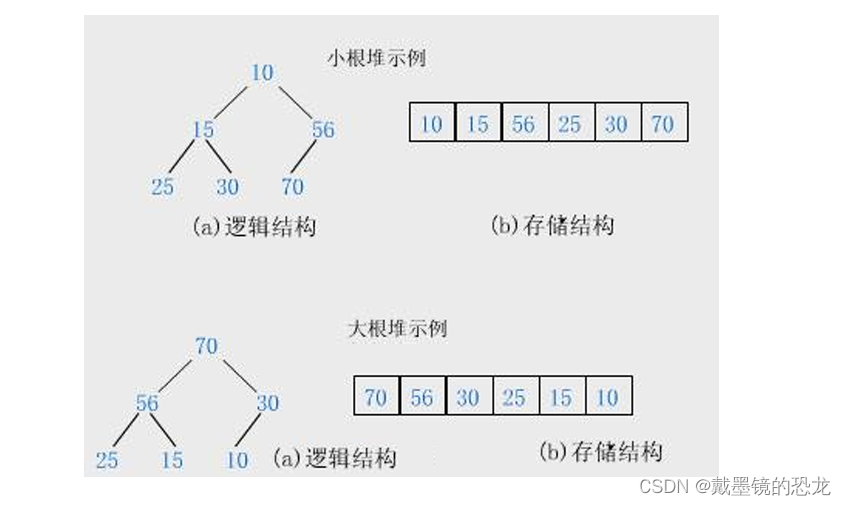
堆:
- 堆是一棵完全二叉树。
- 小堆:任何一个父亲 <= 孩子
- 大堆:任何一个父亲 >= 孩子
- 将根节点最大的堆叫做最大堆或大根堆,
根节点最小的堆叫做最小堆或小根堆
使用堆这种数据结构有什么好处呢?
TopK问题(找最值),最值就在根上。
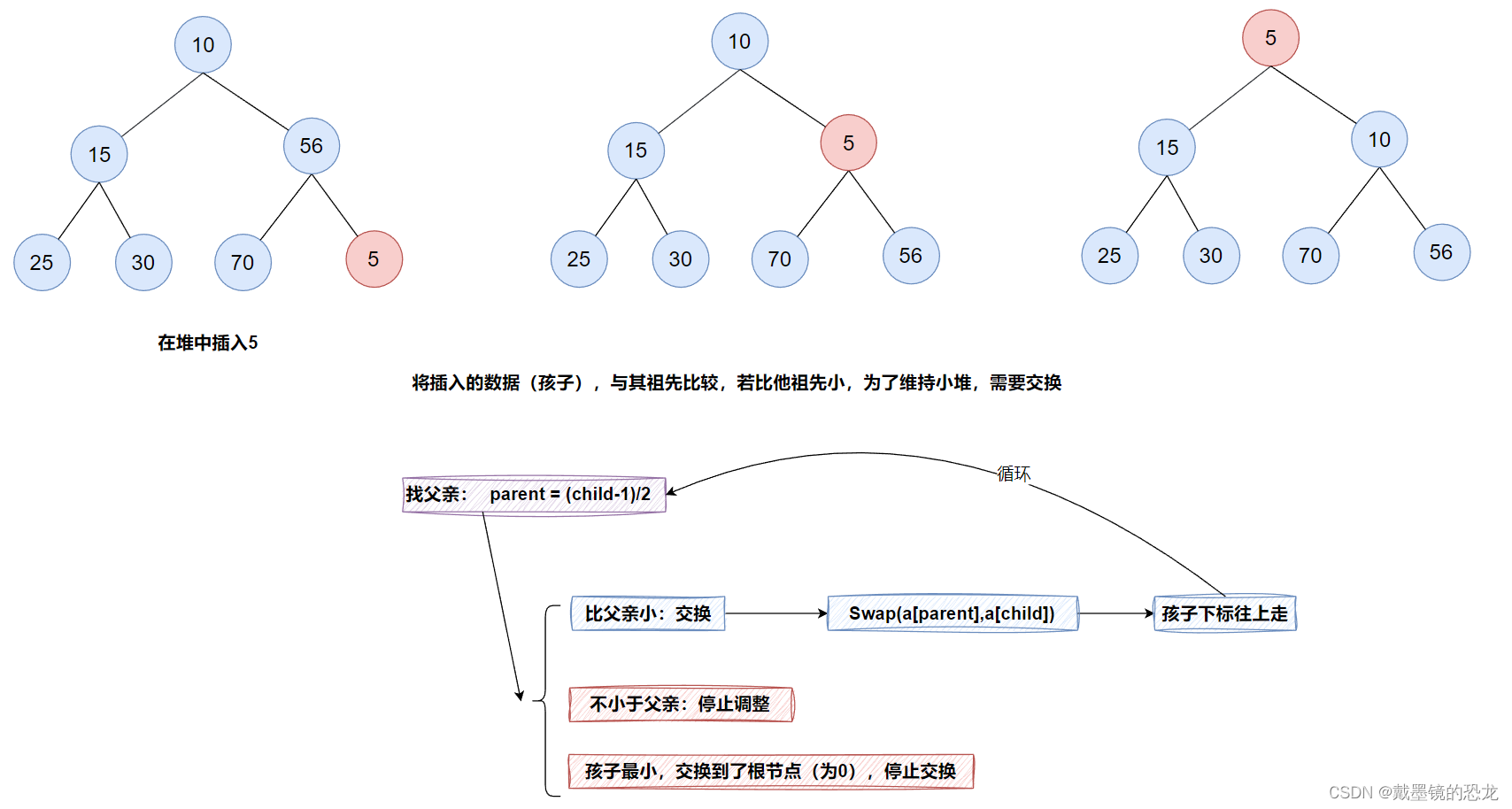
3.1堆的插入(向上调整)
假设已存在一个堆,现需向堆中插入元素5。
void Swap(HeapDataType* x, HeapDataType* y)
{HeapDataType tmp = *x;*x = *y;*y = tmp;
}void AdjustUp(HeapDataType* a, int child)
{int parent = (child - 1) / 2;//while(parent >= 0)while (child){//孩子小于父亲if (a[child] < a[parent]){//交换Swap(&a[child], &a[parent]);//改变下标child = parent;//继续找父亲parent = (child - 1) / 2;}else{break;}}
}// 堆的插入
void HeapPush(Heap* php, HeapDataType x)
{assert(php);//扩容if (php->size == php->capacity){int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HeapDataType* tmp = (HeapDataType*)realloc(php->a, sizeof(HeapDataType)*newcapacity);if (tmp == NULL){perror("realloc");return;}php->a = tmp;php->capacity = newcapacity;}//将数据先插入到堆中php->a[php->size] = x;php->size++;//插入后向上调整,使其仍然是堆//开始调整的位置为数组末尾位置:size-1AdjustUp(php->a, php->size - 1);
}
思考:如何让一个数组变成堆?
将数组的值插入堆中即可
int main()
{Heap* heap = HeapCreate();int arr[] = { 1,4,7,3,9,10 };for (int i = 0; i < sizeof(arr)/sizeof(int); i++){HeapPush(heap, arr[i]);}HeapDestroy(heap);return 0;
}
3.2堆的删除(向下调整)
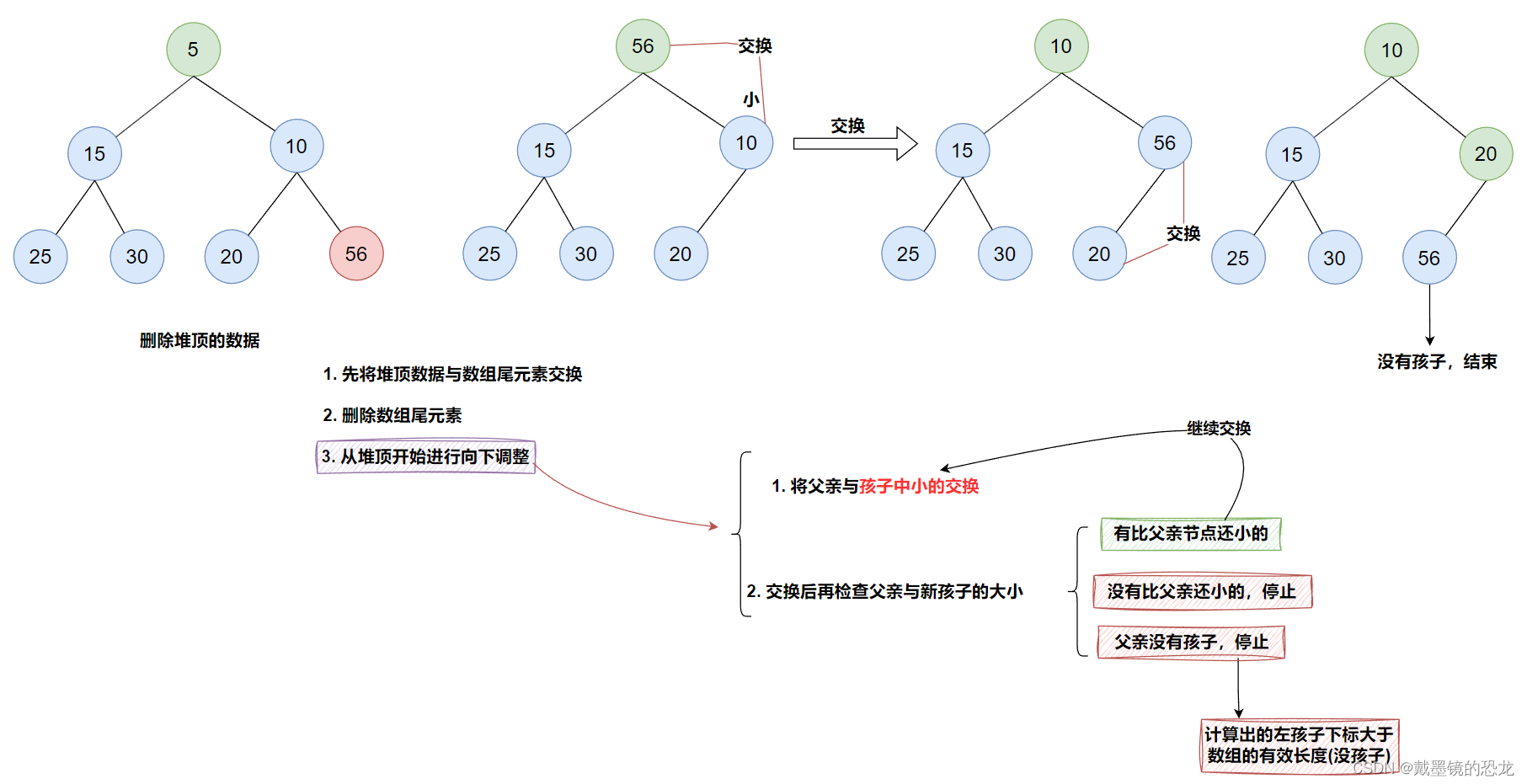
void AdjustDown(HeapDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n)//有左孩子就继续{//找小的孩子//若右孩子存在 且 右孩子小于左孩子,右孩子是小孩子if (child+1 < n && a[child+1] < a[child]){child++;}//小孩子小于父亲,交换if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}// 堆的删除
void HeapPop(Heap* php)
{assert(php);assert(php->size);Swap(&php->a[0], &php->a[php->size - 1]);//交换php->size--;//删除数组尾位置AdjustDown(php->a, php->size, 0);
}
由于向下调整法最多调整高度次,那么它的时间复杂度是O(logN)
3.3堆的创建
下面我们给出一个数组,这个数组逻辑上可以看做一颗完全二叉树,但是还不是一个堆,现在我们通过算法,把它构建成一个堆。根节点左右子树不是堆,我们怎么调整呢?
3.3.1使用向上调整
从数组的第二个元素开始,使其按照小堆/大堆的规则调整成堆
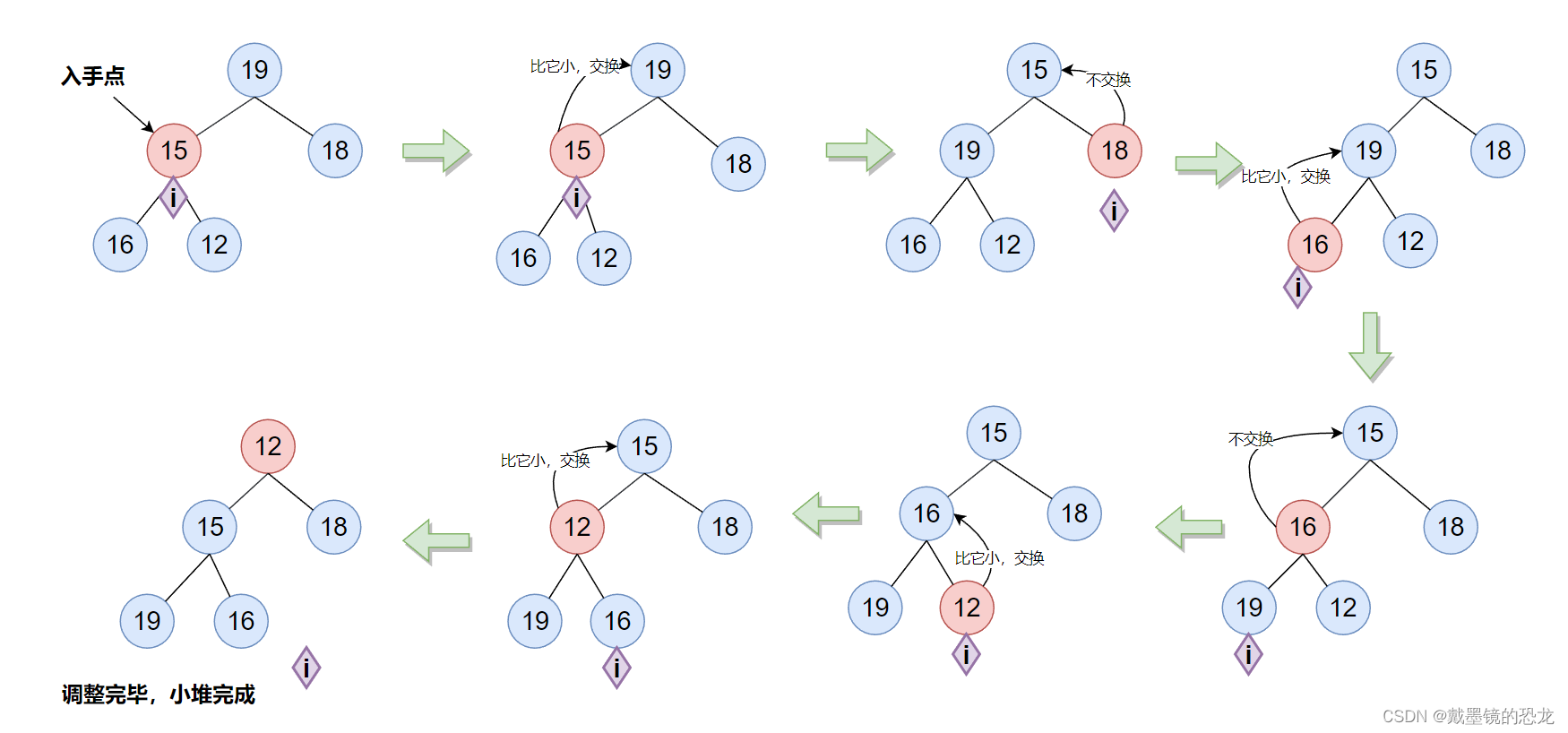
void HeapCreat(Heap* php, HeapDataType* a, int n)
{assert(php);php->a = (HeapDataType*)malloc(sizeof(HeapDataType) * n);//申请和数组同样大的空间if (php->a == NULL){perror("malloc fail");return;}memcpy(php->a, a, sizeof(HeapDataType) * n);//将数组中的元素拷贝进堆php->size = n;php->capacity = n;//向上调整,使其成堆for (int i = 1; i < n; i++){AdjustUp(php->a, i);}
}
3.3.2使用向下调整
用向下调整法,我们从倒数的第一个非叶子节点的子树开始调整,一直调整到根节点的树,就可以调整成堆。
其实本质上就是:从下往上,将根的每个子树调整成堆
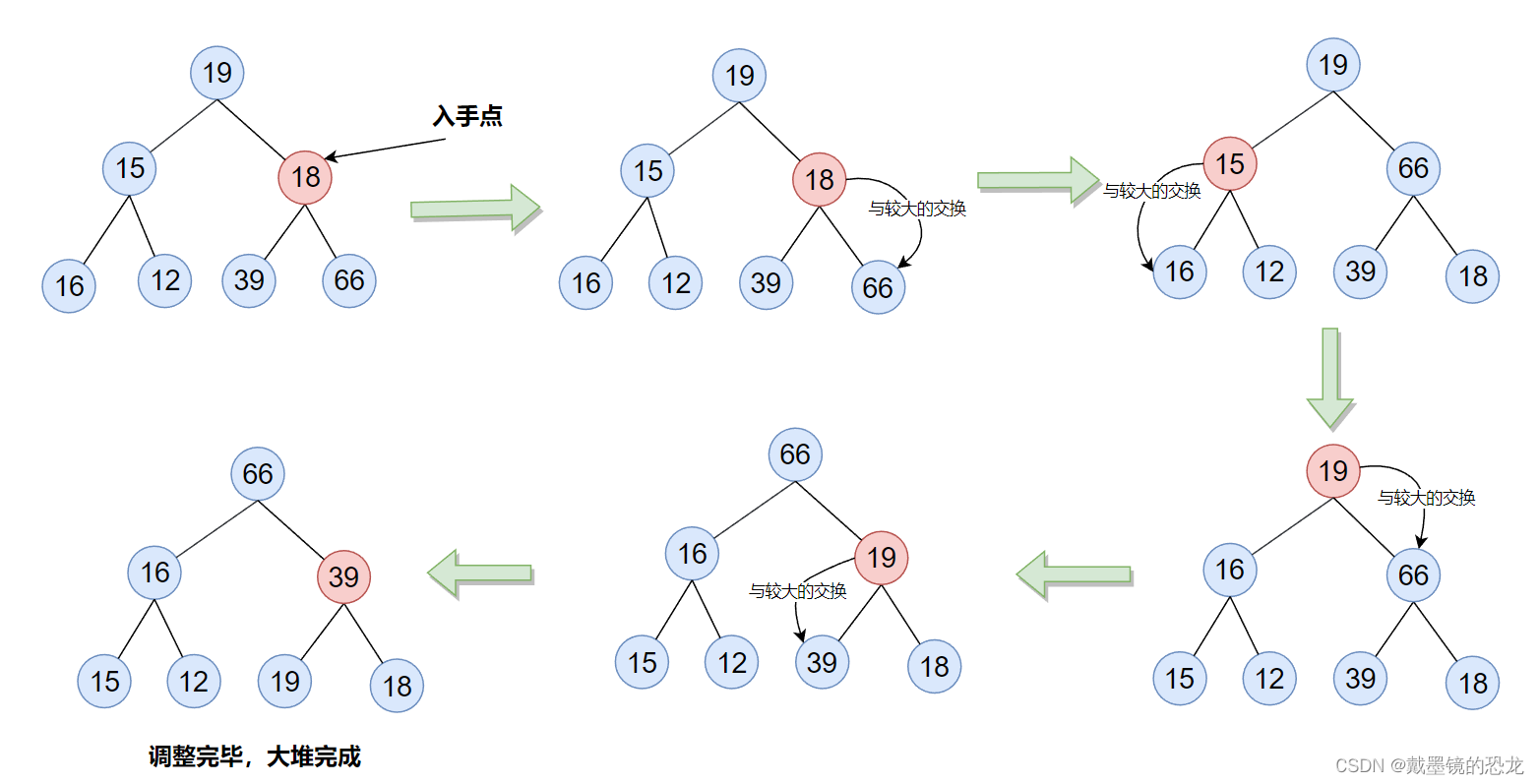
由于最后一个元素的下标为n-1,所以它的父亲应该是:(其下标-1)/2,也就是(n-1-1)/2。
void HeapCreat(Heap* php, HeapDataType* a, int n)
{assert(php);php->a = (HeapDataType*)malloc(sizeof(HeapDataType) * n);//申请和数组同样大的空间if (php->a == NULL){perror("malloc fail");return;}memcpy(php->a, a, sizeof(HeapDataType) * n);//将数组中的元素拷贝进堆php->size = n;php->capacity = n;//向下调整,使其成堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(php->a, n, i);}
}
3.3.3两种建堆方式的比较
- 树的高度与节点个数的关系
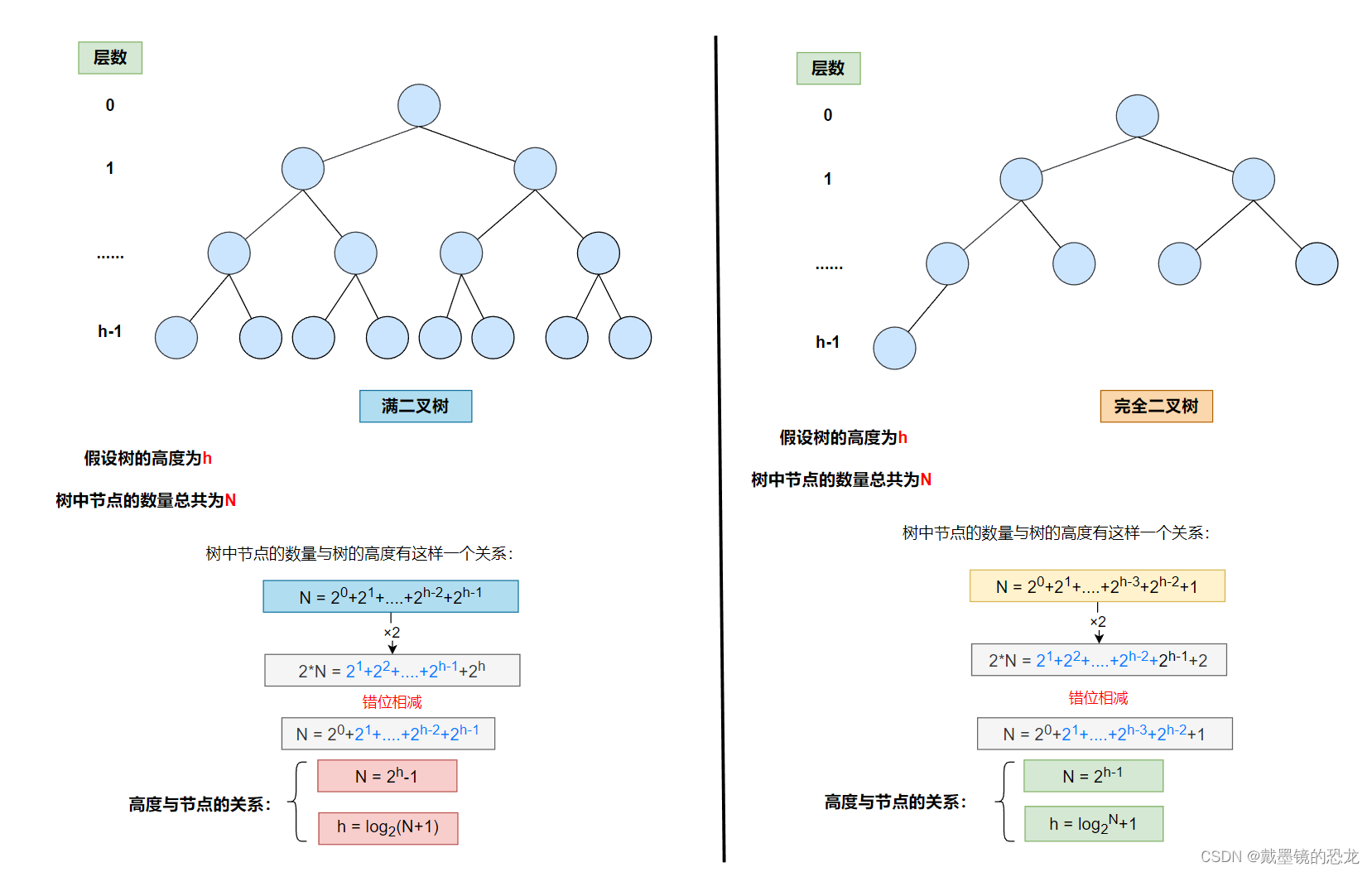
- 向上调整法建堆时间复杂度的分析
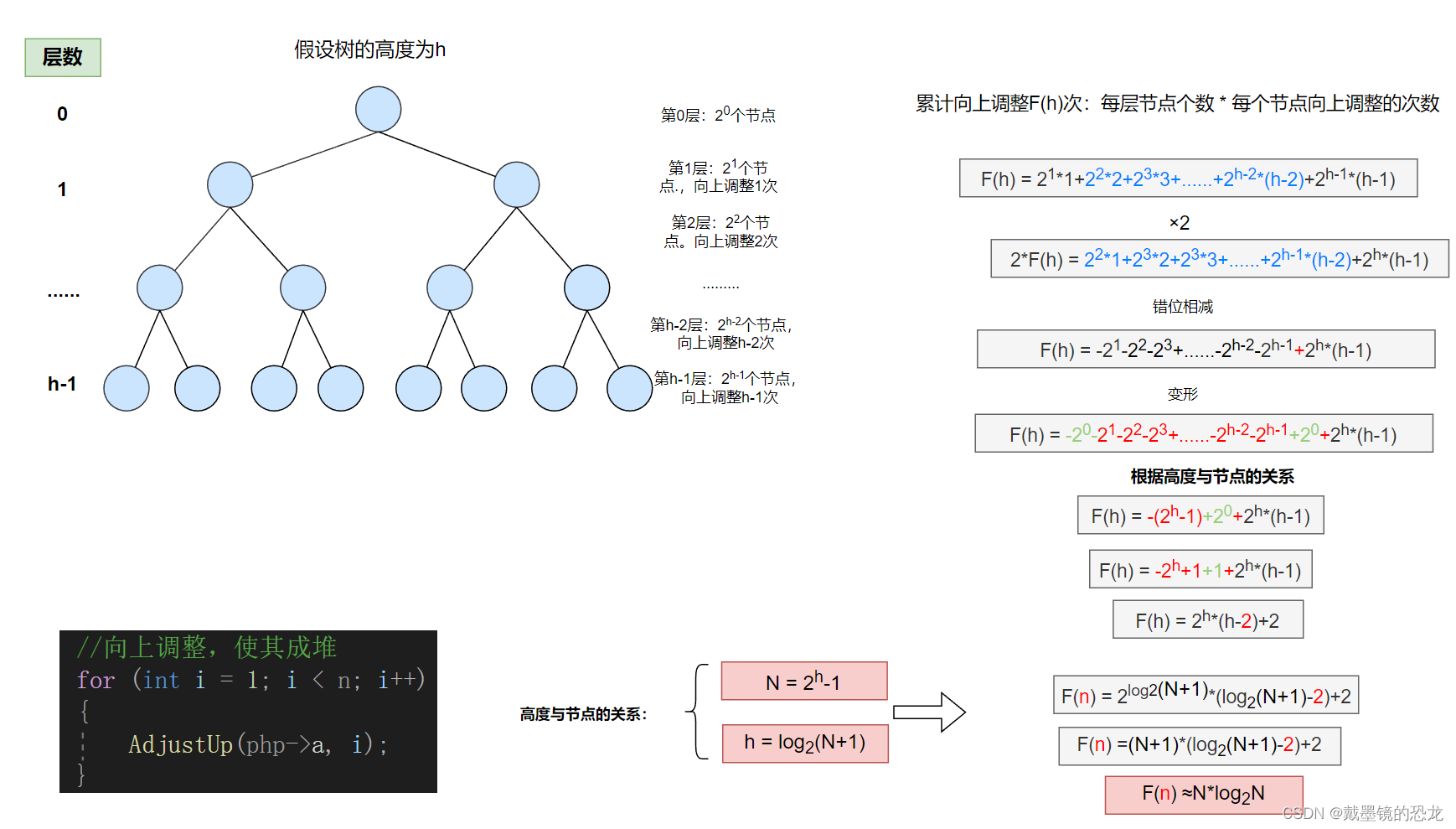
因此,向上调整建堆的时间复杂度为:O(N*log2N)
- 向下调整法建堆时间复杂度的分析
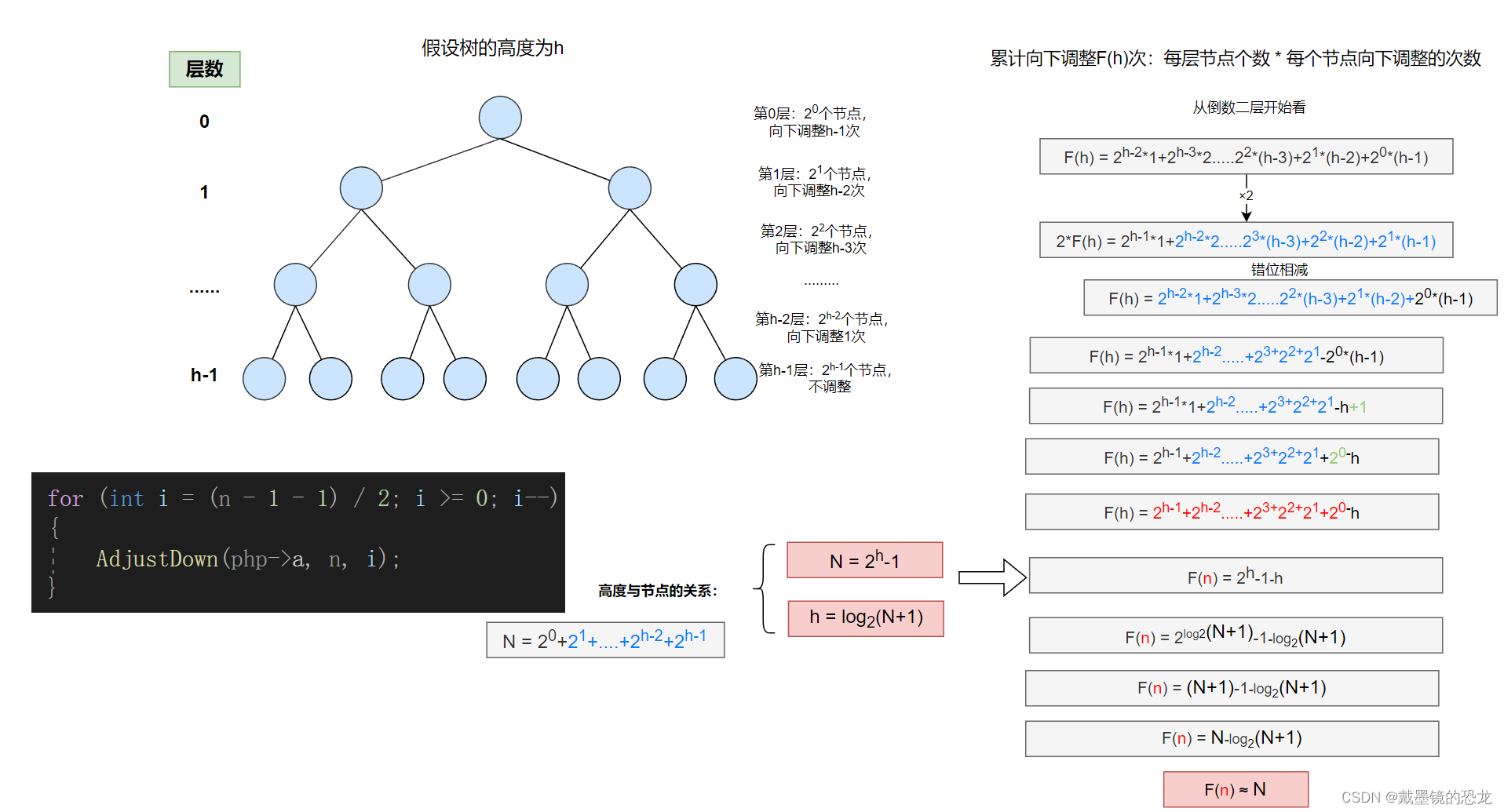
因此,向下调整建堆的时间复杂度为:O(N)
O(N*log2N) 与O(N)看来两种方法的效率差别还是挺大的。为什么差别这么大呢?

3.4堆排序
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
-
建堆
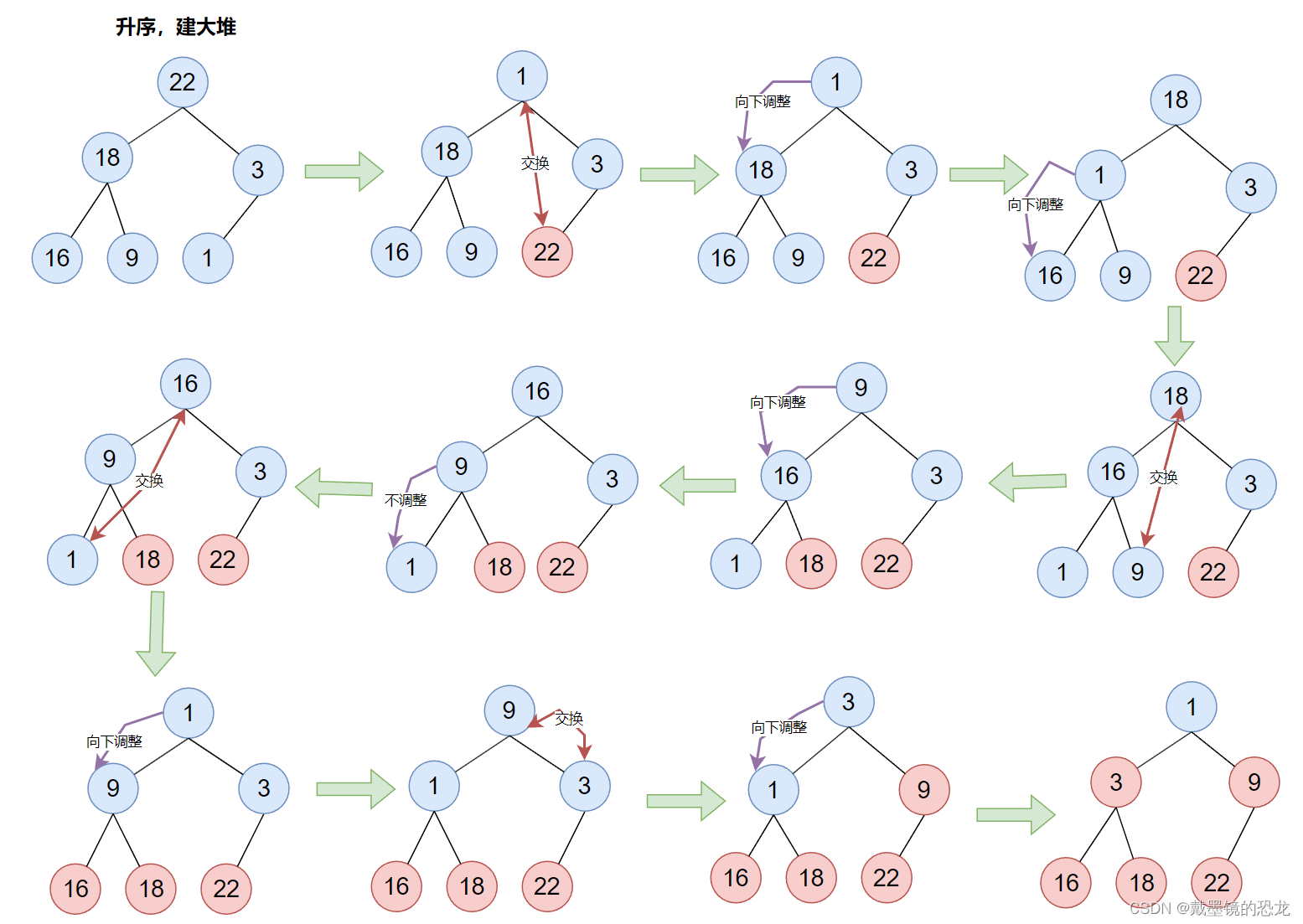
升序:建大堆
降序:建小堆 -
利用堆删除思想来进行排序
首位交换
最后一个值不看做堆里面的,向下调整选出次大的数据
#include<stdio.h>
void _Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}void _AdjustDown(int* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){//右孩子存在,且大于左孩子if (child + 1 < n && a[child + 1] > a[child]){child++;}//孩子大于父亲,交换if (a[child] > a[parent]){_Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;//孩子不大于父亲,调整结束}}
}int main()
{int arr[] = { 3,1,9,18,22,16 };int sz = sizeof(arr) / sizeof(arr[0]);//向下调整建堆for (int i = (sz - 1 - 1) / 2; i >= 0; i--){_AdjustDown(arr, sz, i);}int end = sz - 1;while (end > 0){_Swap(&arr[0], &arr[end]);//首位交换_AdjustDown(arr, end, 0);end--;}for (int i = 0; i < sz; i++){printf("%d ", arr[i]);}return 0;
}
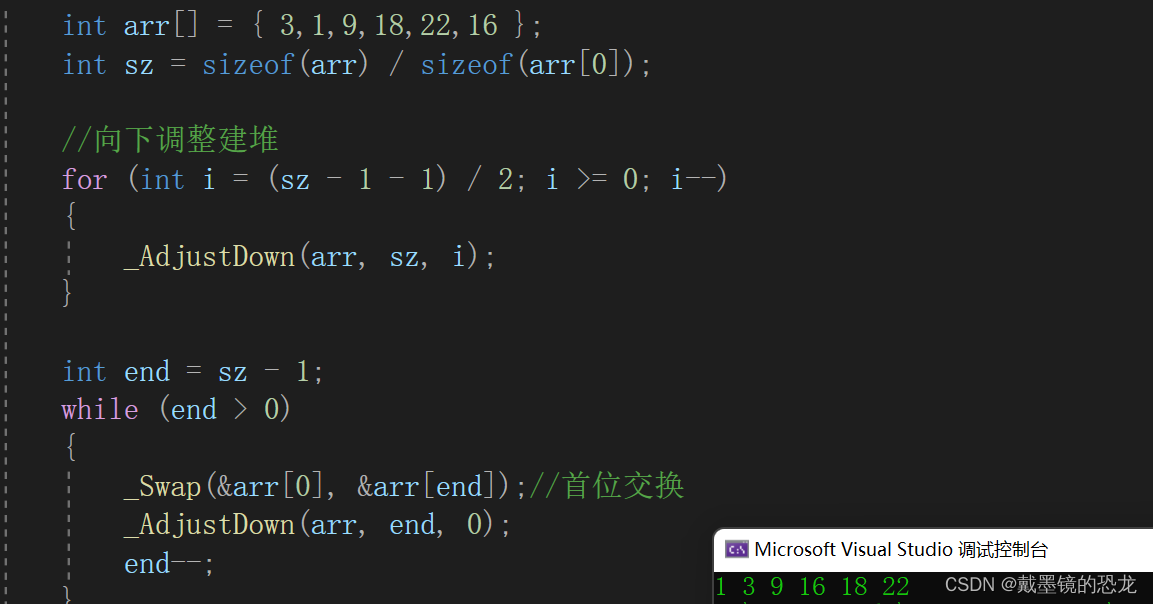
所以堆排序的时间复杂度是:建堆O(N)+每个节点需要调整的次数(N-1)* logN 。 该排序的时间复杂度最终为:N*logN
3.5TopK问题
TOP-K问题:即求数据中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
- 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆 - 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
- 将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
void TopK(int k)
{FILE* fp = fopen("data.txt", "r");if (fp == NULL){return;}int* heap = (int*)malloc(sizeof(int) * k);if (heap == NULL){perror("malloc fail");return;}//先读取k个数据for (int i = 0; i < k; i++){fscanf(fp, "%d", &heap[i]);}//根据k个数据建小堆for (int i = (k - 1 - 1) / 2; i >= 0; i--){_AdjustDown(heap, k, i);}int num = 0;while (fscanf(fp, "%d", &num) != EOF){//读取堆顶数据,比它大就替换它,进堆if (num > heap[0]){heap[0] = num;_AdjustDown(heap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", heap[i]);}fclose(fp);
}
相关文章:

【数据结构】树与堆 (向上/下调整算法和复杂度的分析、堆排序以及topk问题)
文章目录 1.树的概念1.1树的相关概念1.2树的表示 2.二叉树2.1概念2.2特殊二叉树2.3二叉树的存储 3.堆3.1堆的插入(向上调整)3.2堆的删除(向下调整)3.3堆的创建3.3.1使用向上调整3.3.2使用向下调整3.3.3两种建堆方式的比较 3.4堆排…...

安装CDH平台的服务器磁盘满了,磁盘清理过程记录
1.使用hdfs命令查看哪个文件占用最大 hdfs dfs -du -h /tmp 2.我的服务器上显示/tmp/hive/hive文件夹下的,一串字符串命名的文件特别大几乎把磁盘占满了 网上查到/tmp文件是临时文件,由于hiveserver2任务运行异常导致缓存未删除,正常情况下…...

《互联网的世界》第七讲-能源
本想聊聊 tcp 和 quic,但这些都属于术的范畴,变化多端,等孩子们长大了又不知变成什么样子了,趁这段时间在家,还是得讲一些相对不变的东西,或法或势。 从 安阳卖血糕的精巧篦子 想到如何做圆米粉和圆面条&a…...

前端代码整洁与规范之CSS篇
一、代码整洁 1. 命名规范 CSS 类名的命名应该简洁清晰,能够准确描述元素的作用。避免使用无意义的名称,例如“a”、“b”等,而应该使用有意义的英文单词或单词缩写。同时,也要避免使用驼峰命名法和下划线命名法混杂使用&#x…...
在【IntelliJ IDEA】中配置【Tomcat】【2023版】【中文】【图文详解】
作为一款功能强大的集成开发环境(IDE),IntelliJ IDEA为Web服务器提供了卓越的支持,从而极大地简化了程序员在Web开发过程中的工作流程。学习Java Web开发实质上就是掌握如何创造动态Web资源,这些资源在完成开发后&…...
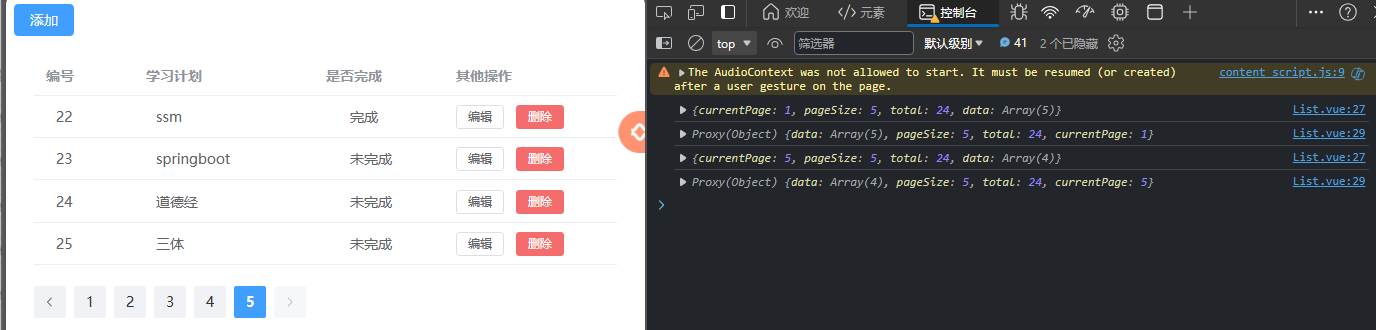
【SSM】任务列表案例 基本CRUD SSM整合
文章目录 一、案例功能预览二、接口分析三、前端工程导入四、后端程序实现和测试4.1 准备4.2 功能实现4.2.1 分页查询显示4.2.2 添加计划4.2.2 删除计划4.2.3 修改计划 4.3 前后联调 一、案例功能预览 Github 地址 : ssm-integration-part 二、接口分析 学习计划…...
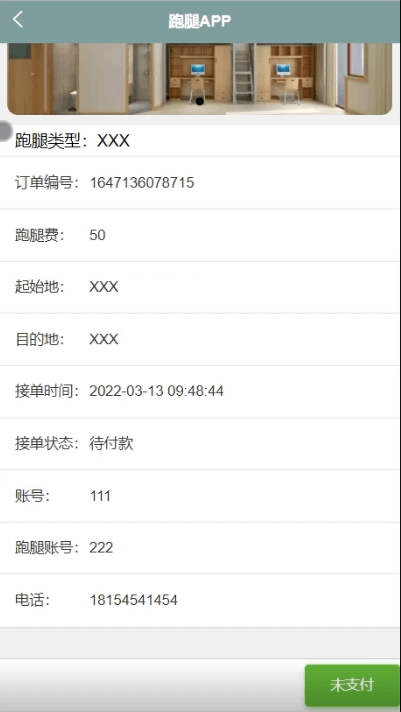
基于微信小程序的校园跑腿小程序,附源码
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...
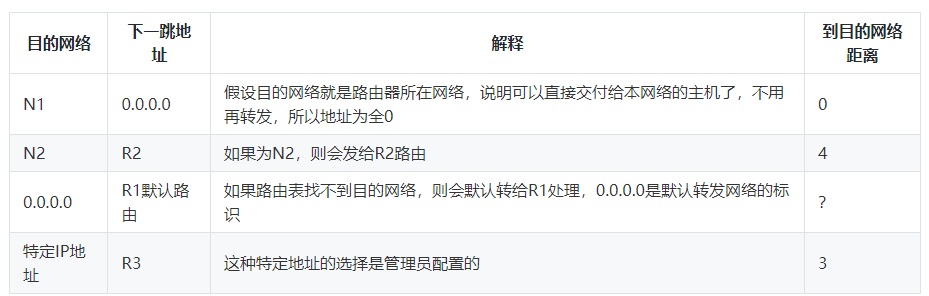
网络学习:9个计算机的“网络层”知识点
目录 一、IP 地址 1.1 分类表示法: 1.1.1 分类表示地址的其他说明 1.2 无分类编址 CIDR 二、IP 数据报文格式 Q: IP 报文里有什么?可以不按顺序或者字节来讲一讲 三、 路由概念 3.1 路由表 3.2 路由网络匹配 3.3 ARP 解析 3.4 RARP 逆地址解析…...
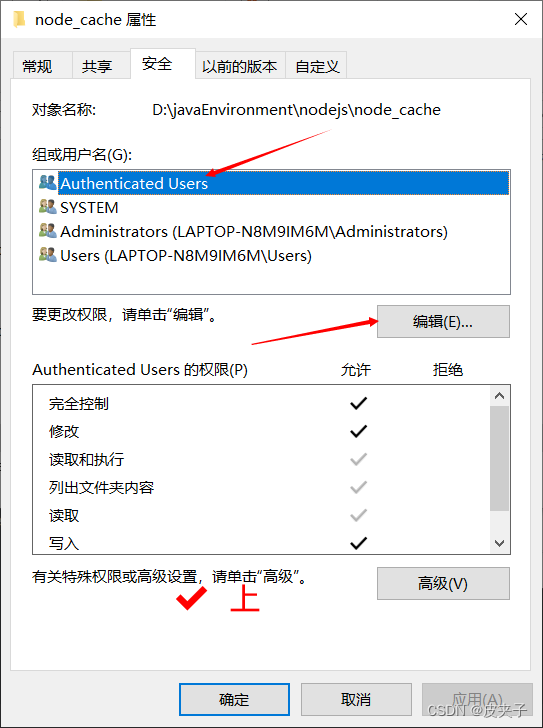
web项目的搭建
使用Webstorm并创建Next.js文件 1、配置nodejs环境、安装webstorm【配置node.js可以使用nvm去管理nodejs的版本】 2、需要破解webstorm,可能会导致原本的idea失效,注册码过期 3、taobao的npm过期,导致npm is sass执行不成功,需…...

C++for语句
1.求平均年龄 班上有学生若干名,给出每名学生的年龄(整数),求班上所有学生的平均年龄,保留到小数点后两位 输入 第1行有一个整数n(1 <= n <=100),表示学生的人数;其后n行每行有1个整数,表示每个学生的年龄,取值为15~25 输出 一行,包含一个浮点数,为所求的平…...

最新基于R语言lavaan结构方程模型(SEM)技术
原文链接:最新基于R语言lavaan结构方程模型(SEM)技术https://mp.weixin.qq.com/s?__bizMzUzNTczMDMxMg&mid2247596681&idx4&sn08753dd4d3e7bc492d750c0f06bba1b2&chksmfa823b6ecdf5b278ca0b94213391b5a222d1776743609cd3d14…...
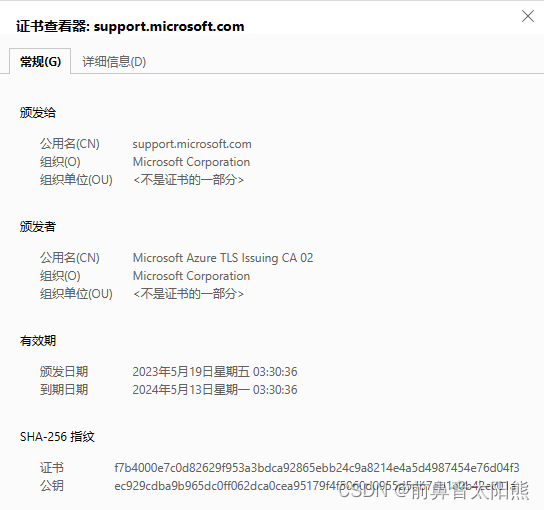
【网络安全】-数字证书
数字证书 数字证书是互联网通讯中用于标志通讯各方身份信息的一串数字或数据,它为网络应用提供了一种验证通信实体身份的方式。具体来说,数字证书是由权威的证书授权(CA)中心签发的,包含公开密钥拥有者信息以及公开密…...

【C++ 】stack 和 queue
1. 标准库中的stack stack 的介绍: 1. stack是一种容器适配器,专门用在具有后进先出操作的上下文环境中,其删除只能从容器的一端进行 元素的插入与提取操作 2. stack是作为容器适配器被实现的,容器适配器即是对特定类封装作为其…...

html--彩虹马
文章目录 htmljscss 效果 html <!DOCTYPE html> <html lang"en" > <head> <meta charset"UTF-8"> <title>Rainbow Space Unicorn</title> <link rel"stylesheet" href"css/style.css"> &l…...
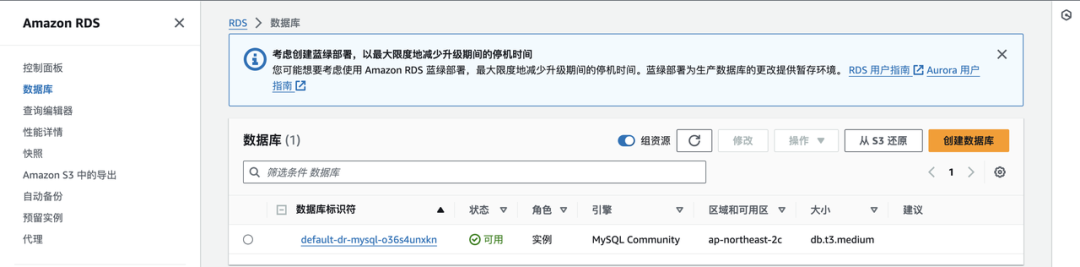
如何将应用一键部署至多个环境?丨Walrus教程
在 Walrus 平台上,运维团队在资源定义(Resource Definition)中声明提供的资源类型,通过设置匹配规则,将不同的资源部署模板应用到不同类型的环境、项目等。与此同时,研发人员无需关注底层具体实现方式&…...

Redis的一些问题,解决并发的
项目通布隆过滤器: 布隆过滤器: 布隆过滤器是一种空间效率非常高的数据结构,用于快速判断一个元素是否可能存在于一个集合中。它由一个位数组(通常是长度为 m 的比特数组)和 k 个不同的哈希函数组成。当一个元素被加入…...

郭炜老师mooc第十一章数据分析和展示(numpy,pandas, matplotlib)
多维数组库numpy numpy创建数组的常用函数 # numpy数组import numpy as np #以后numpy简写为np print(np.array([1,2,3])) #>>[1 2 3] print(np.arange(1,9,2)) #>>[1 3 5 7] 不包括9 print(np.linspace(1,10,4)) #>>[ 1. 4. 7. 10.] # linespace(x,y,n)&…...
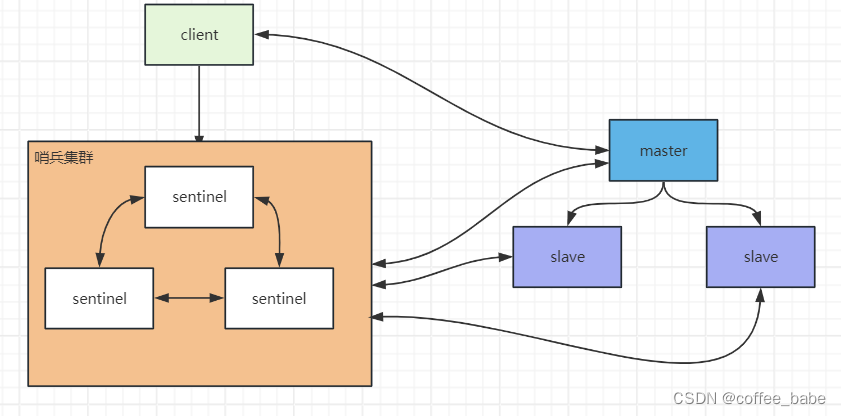
Redis主从架构和管道Lua(一)
Redis主从架构 架构 Redis主从工作原理 如果为master配置了一个slave,不管这个slave是否是第一次连接上Master,它都会发送一个PSYNC命令给master请求复制数据。master受到PSYNC命令,会在后台进行数据持久化通过bgsave生成最新的 RDB快照文件,持久化期间…...

GTH手册学习注解
CPLL的动态配置 终于看到有这个复位功能了 QPLL SWITCHing需要复位 器件级RESET没发现有管脚引出来 两种复位方式,对应全复位和器件级复位 对应的复位功能管脚 改那个2分频的寄存器说明段,复位是自动发生的?说明可能起效了,但是分…...

html5cssjs代码 002 50以内的加法算式
html5&css&js代码 002 一些基本概念 50以内的加法算式 一、代码二、解释 50以内的加法算式。 一、代码 <!DOCTYPE html> <html lang"en"> <head><title>50以内的加法算式</title><meta charset"UTF-8"><m…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...
