web项目的搭建
使用Webstorm并创建Next.js文件
1、配置nodejs环境、安装webstorm【配置node.js可以使用nvm去管理nodejs的版本】
2、需要破解webstorm,可能会导致原本的idea失效,注册码过期
3、taobao的npm过期,导致npm is sass执行不成功,需要更换
1、以管理员方式运行cmd
2、清空缓存:npm cache clean --force
3、设置新的淘宝镜像源
npm config set registry https://registry.npmmirror.com
4、需要将配置权限打开,

5、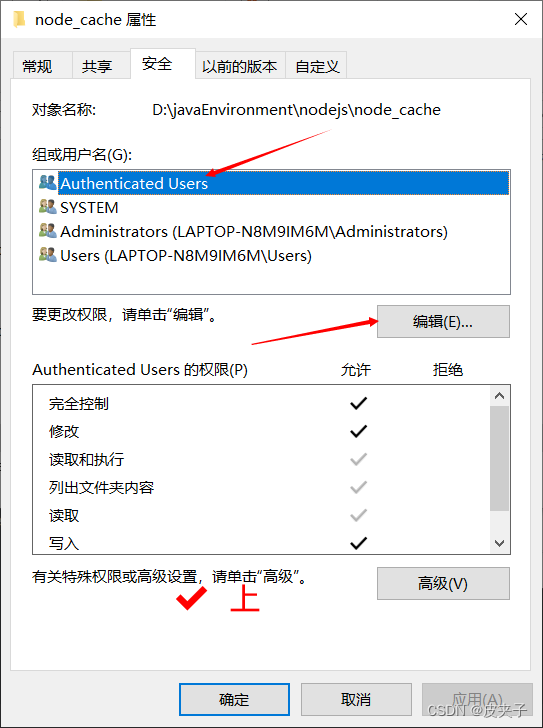
5、直接运行项目会报错,需要自己创建项目
- ‘next’ 不是内部或外部命令,也不是可运行的程序 或批处理文件。
6、创建项目会问npm install命令是否执行,需要执行,用于在项目中安装所需的依赖包。它会读取项目目录中的 “package.json” 文件,并从 npm registry 下载定义的依赖包
7、创建next.js项目需要系统自己创建src目录,手动创建会导致page.tsx文件导出失败
8、无法从终端运行npm等命令
- 比如npm i sass等命令
1.在Windows应用中找到Windows PowerShell。
2.右键以管理员运行。
3.在命令框输入: set-ExecutionPolicy RemoteSigned。
4.回车。
5.根据提示输入A,然后回车
teSigned。
4.回车。
5.根据提示输入A,然后回车
相关文章:

web项目的搭建
使用Webstorm并创建Next.js文件 1、配置nodejs环境、安装webstorm【配置node.js可以使用nvm去管理nodejs的版本】 2、需要破解webstorm,可能会导致原本的idea失效,注册码过期 3、taobao的npm过期,导致npm is sass执行不成功,需…...

C++for语句
1.求平均年龄 班上有学生若干名,给出每名学生的年龄(整数),求班上所有学生的平均年龄,保留到小数点后两位 输入 第1行有一个整数n(1 <= n <=100),表示学生的人数;其后n行每行有1个整数,表示每个学生的年龄,取值为15~25 输出 一行,包含一个浮点数,为所求的平…...

最新基于R语言lavaan结构方程模型(SEM)技术
原文链接:最新基于R语言lavaan结构方程模型(SEM)技术https://mp.weixin.qq.com/s?__bizMzUzNTczMDMxMg&mid2247596681&idx4&sn08753dd4d3e7bc492d750c0f06bba1b2&chksmfa823b6ecdf5b278ca0b94213391b5a222d1776743609cd3d14…...
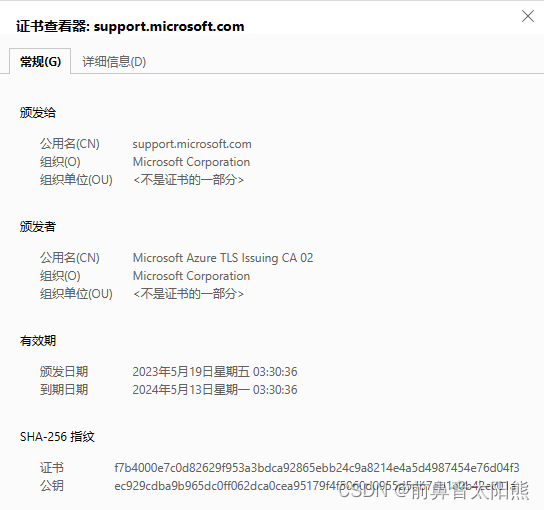
【网络安全】-数字证书
数字证书 数字证书是互联网通讯中用于标志通讯各方身份信息的一串数字或数据,它为网络应用提供了一种验证通信实体身份的方式。具体来说,数字证书是由权威的证书授权(CA)中心签发的,包含公开密钥拥有者信息以及公开密…...

【C++ 】stack 和 queue
1. 标准库中的stack stack 的介绍: 1. stack是一种容器适配器,专门用在具有后进先出操作的上下文环境中,其删除只能从容器的一端进行 元素的插入与提取操作 2. stack是作为容器适配器被实现的,容器适配器即是对特定类封装作为其…...

html--彩虹马
文章目录 htmljscss 效果 html <!DOCTYPE html> <html lang"en" > <head> <meta charset"UTF-8"> <title>Rainbow Space Unicorn</title> <link rel"stylesheet" href"css/style.css"> &l…...
如何将应用一键部署至多个环境?丨Walrus教程
在 Walrus 平台上,运维团队在资源定义(Resource Definition)中声明提供的资源类型,通过设置匹配规则,将不同的资源部署模板应用到不同类型的环境、项目等。与此同时,研发人员无需关注底层具体实现方式&…...

Redis的一些问题,解决并发的
项目通布隆过滤器: 布隆过滤器: 布隆过滤器是一种空间效率非常高的数据结构,用于快速判断一个元素是否可能存在于一个集合中。它由一个位数组(通常是长度为 m 的比特数组)和 k 个不同的哈希函数组成。当一个元素被加入…...

郭炜老师mooc第十一章数据分析和展示(numpy,pandas, matplotlib)
多维数组库numpy numpy创建数组的常用函数 # numpy数组import numpy as np #以后numpy简写为np print(np.array([1,2,3])) #>>[1 2 3] print(np.arange(1,9,2)) #>>[1 3 5 7] 不包括9 print(np.linspace(1,10,4)) #>>[ 1. 4. 7. 10.] # linespace(x,y,n)&…...
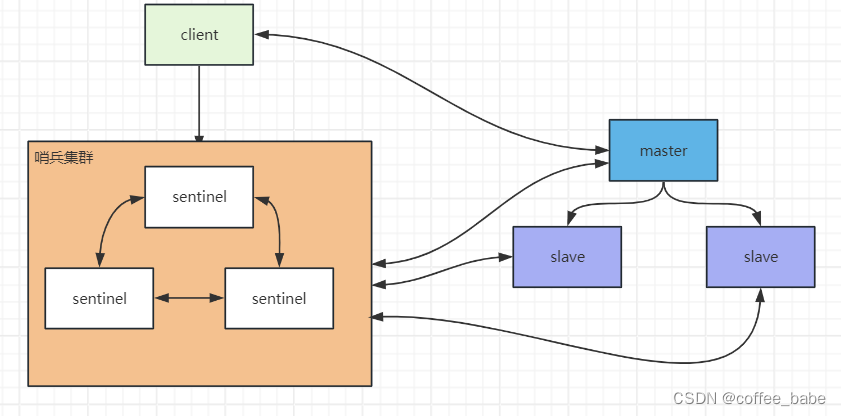
Redis主从架构和管道Lua(一)
Redis主从架构 架构 Redis主从工作原理 如果为master配置了一个slave,不管这个slave是否是第一次连接上Master,它都会发送一个PSYNC命令给master请求复制数据。master受到PSYNC命令,会在后台进行数据持久化通过bgsave生成最新的 RDB快照文件,持久化期间…...

GTH手册学习注解
CPLL的动态配置 终于看到有这个复位功能了 QPLL SWITCHing需要复位 器件级RESET没发现有管脚引出来 两种复位方式,对应全复位和器件级复位 对应的复位功能管脚 改那个2分频的寄存器说明段,复位是自动发生的?说明可能起效了,但是分…...

html5cssjs代码 002 50以内的加法算式
html5&css&js代码 002 一些基本概念 50以内的加法算式 一、代码二、解释 50以内的加法算式。 一、代码 <!DOCTYPE html> <html lang"en"> <head><title>50以内的加法算式</title><meta charset"UTF-8"><m…...
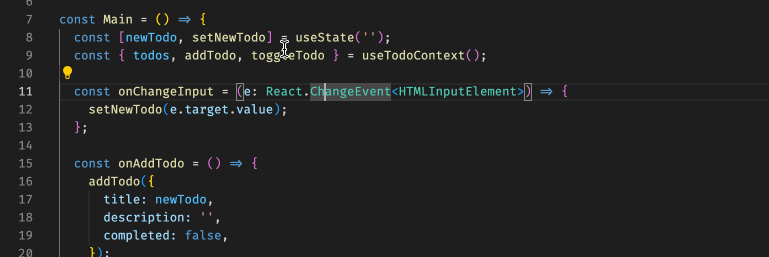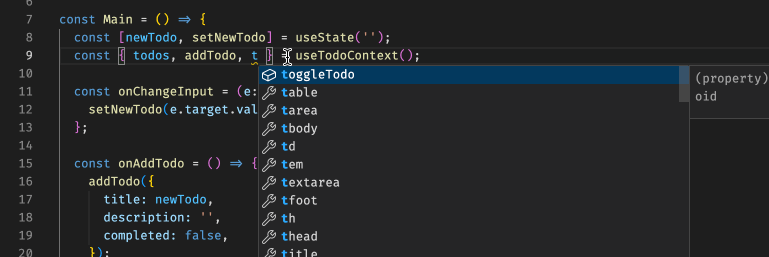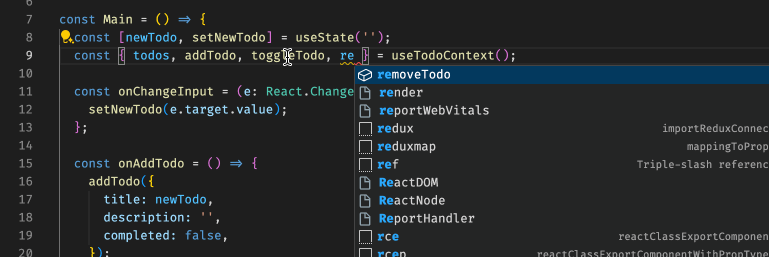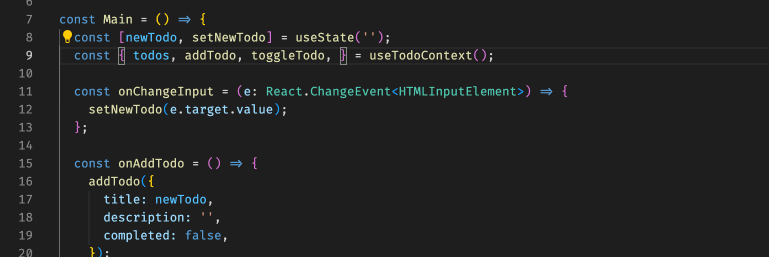
[React 进阶系列] React Context 案例学习:使用 TS 及 HOC 封装 Context
[React 进阶系列] React Context 案例学习:使用 TS 及 HOC 封装 Context 具体 context 的实现在这里:[React 进阶系列] React Context 案例学习:子组件内更新父组件的状态。 根据项目经验是这样的,自从换了 TS 之后,…...

网络编程:网络编程基础
一、网络发展 1.TCP/IP两个协议阶段 TCP/IP协议已分成了两个不同的协议: 用来检测网络传输中差错的传输控制协议TCP 专门负责对不同网络进行2互联的互联网协议IP 2.网络体系结构 OSI体系口诀:物链网输会示用 2.1网络体系结构概念 每一层都有自己独…...
力扣热题100_矩阵_73_矩阵置零
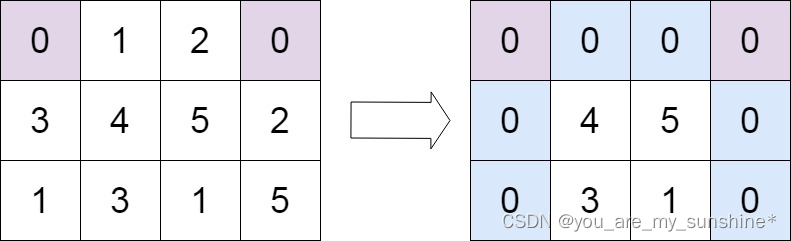
文章目录 题目链接解题思路解题代码 题目链接 73.矩阵置零 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 示例 1: 输入:matrix [[1,1,1],[1,0,1],[1,1,1]] 输出&…...

C++程序设计-第四/五章 函数和类和对象【期末复习|考研复习】
前言 总结整理不易,希望大家点赞收藏。 给大家整理了一下C程序设计中的重点概念,以供大家期末复习和考研复习的时候使用。 C程序设计系列文章传送门: 第一章 面向对象基础 第四/五章 函数和类和对象 第六/七/八章 运算符重载/包含与继承/虚函…...
C#快速入门基础
本篇文章从最基础的C#编程开始学习,经过非常优秀的面向对象编程思想和方法的学习,为C#编程打下基础。 第 01 章 C#开发环境之VS使用和.NET平台基础 1.1 Visual Studio 开发环境 1.1.1 硬件环境 i5CPUi5CPU(建议 4核 4线程或以上 ࿰…...
UnityShader常用算法笔记(颜色叠加混合、RGB-HSV-HSL的转换、重映射、UV序列帧动画采样等,持续更新中)
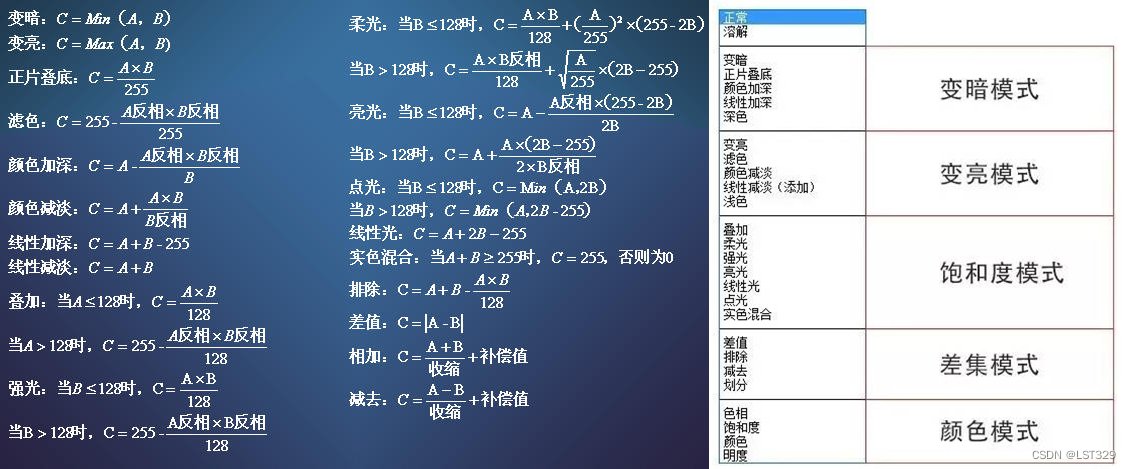
一.颜色叠加混合 1.Blend混合 // 正常,透明度混合 Normal Blend SrcAlpha OneMinusSrcAlpha //柔和叠加 Soft Additive Blend OneMinusDstColor One //正片叠底 相乘 Multiply Blend DstColor Zero //两倍叠加 相加 2x Multiply Blend DstColor SrcColor //变暗…...
Vue3调用钉钉api,内嵌H5微应用单点登录对接
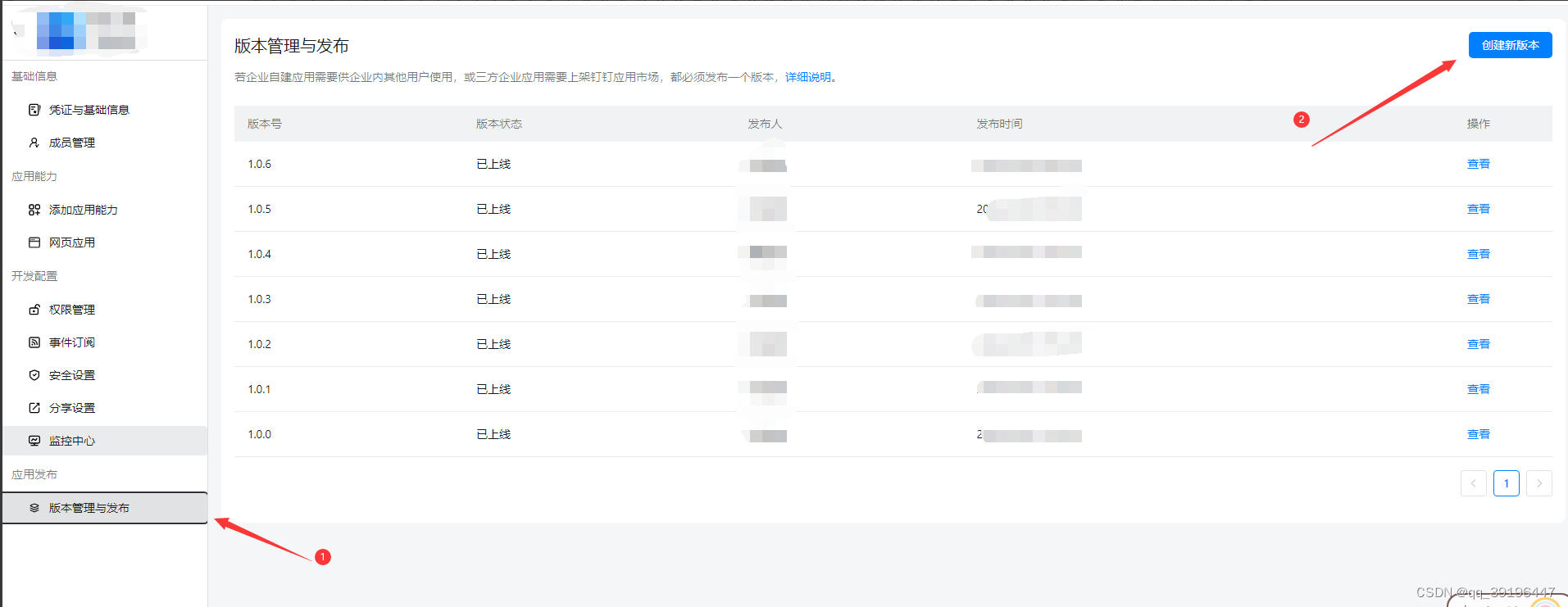
钉钉内嵌H5微应用单点登录对接 https://open.dingtalk.com/document/isvapp/obtain-the-userid-of-a-user-by-using-the-log-free 前端需要的代码 1、安装 dingtalk-jsapi npm install dingtalk-jsapi2、在所需页面引入 import * as dd from dingtalk-jsapi; // 引入钉钉a…...
UE5 局域网联机,寻找会话失败。
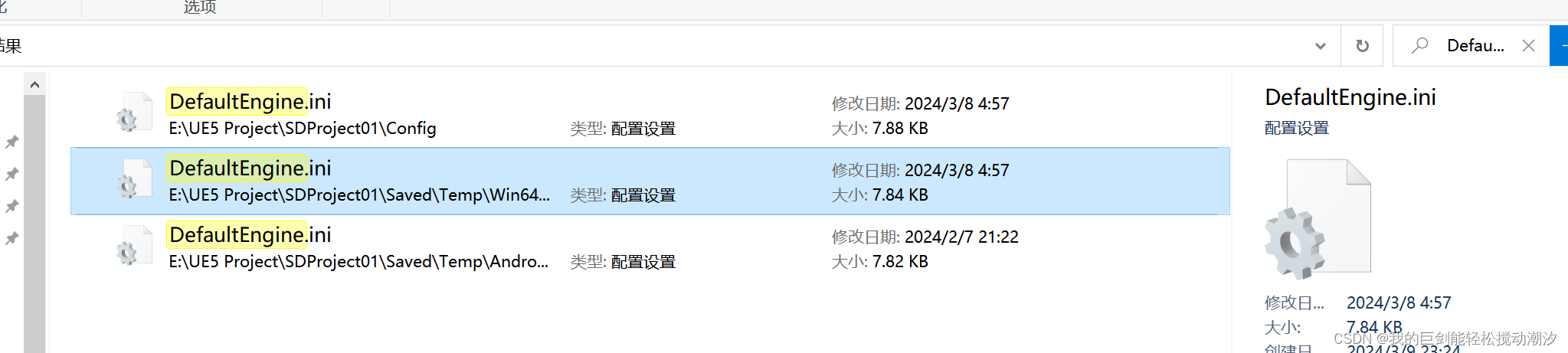
目录 参考资料: 尝试解决办法 1.1在【项目名.Build.cs】脚本中添加该行,添加后关闭编辑器,重新生成解决方案。编辑 2.检查是否在同一个C类子网 参考资料: 1.Cant find session in LAN - Programming & Scripting / Mul…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
