二叉搜索树、B-树、B+树
二叉搜索树
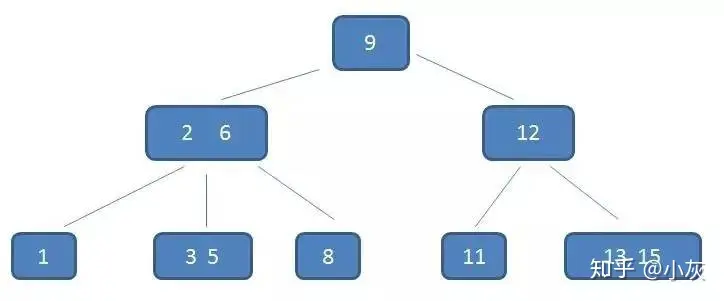
二叉查找树,也称为二叉搜索树、有序二叉树或排序二叉树,是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉搜索树;
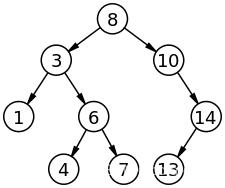
如果二叉查找树是平衡的则查找、插入的时间复杂度为O(logn)。如果二叉查找树完全不平衡则时间复杂度为O(n)。
中序遍历二叉搜索树可以获得关键字的递增序列
二叉搜索树的查找算法
在二叉查找树b中查找x的过程为:
- 若b是空树,则搜索失败,否则:
- 若x等于b的根节点的值,则查找成功;否则:
- 若x小于b的根节点的值,则搜索左子树;否则:
- 查找右子树。
二叉搜索树的节点插入算法
向一个二叉搜索树b中插入一个节点s的算法,过程为:
- 若b是空树,则将s所指节点作为根节点插入,否则:
- 若s->data等于b的根节点的值,则返回,否则:
- 若s->data小于b的根节点的值,则把s所指节点插入到左子树中,否则:
- 把s所指节点插入到右子树中。(新插入节点总是叶子节点)
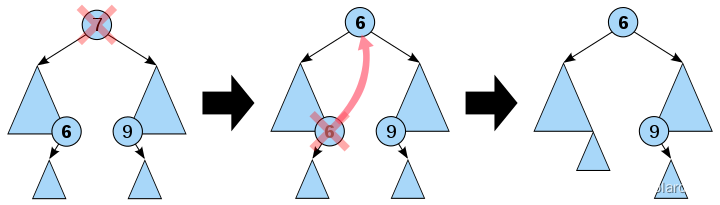
二叉搜索树的节点删除算法
- 若待删除节点*p为叶子节点则直接删除即可
- 若待删除节点*p只有左子树PL或右子树PR,则当*p是左子树(右子树)时直接令PL或PR成为其父节点*f的左子树(右子树)
- 若待删除节点*p的左子树或右子树均不为空,
- 其一是令*p的左子树为*f的左/右(依*p是*f的左子树还是右子树而定)子树,*s为*p左子树的最右下的结点,而*p的右子树为*s的右子树;
- 其二是令*p的直接前驱或直接后继替代*p,然后再从二叉查找树中删去它的直接前驱(或直接后继)。
AVL树
AVL树得名于它的发明者格奥尔吉·阿杰尔松-韦利斯基和叶夫根尼·兰迪斯,他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。
AVL树是一种自平衡二叉搜索树,在AVL树中任一节点对应的两棵子树的最大高度差为1,查找、插入和删除在平均和最坏情况下的时间复杂度都是O(log n),增加和删除元素的操作则可能需要借由一次或多次树旋转,以实现树的重新平衡。
平衡因子:节点的平衡因子是它的左子树的高度减去它的右子树的高度(有时相反)。
旋转操作:
- 右旋
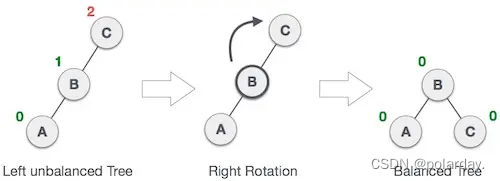
- 左旋

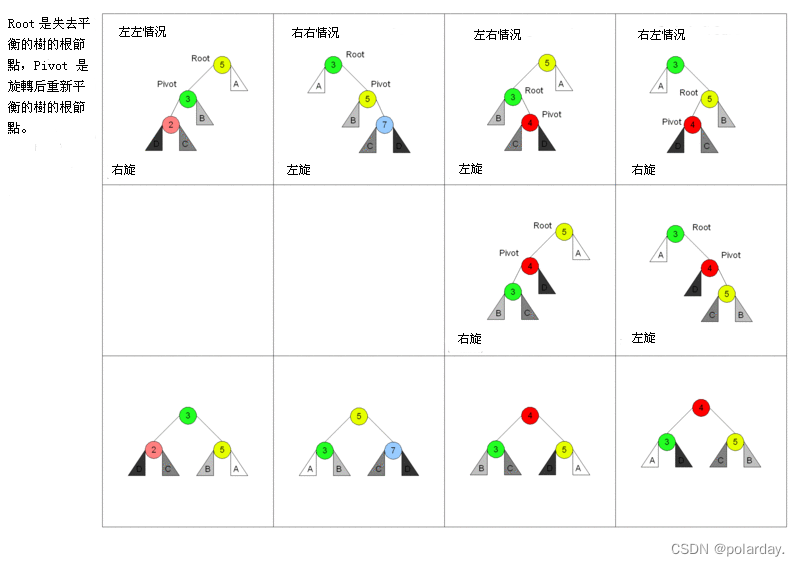
需要平衡的四种情况:
B-树
参考文章
B-树就是B树,中间的横线并不是减号
为什么数据库索引使用B-树而不是二叉搜索树?
考虑磁盘IO的问题,数据库索引是存储在磁盘上的,当数据量比较大的时候,索引的大小可能有几个G甚至更多,当我们利用索引查询的时候只能逐一加载每一个磁盘页这里的磁盘页对应索引树的节点,最坏情况下磁盘IO次数等于索引树的高度,所以需要把原本“瘦高”的树结构变得“矮胖”,这就是B-树的特征之一。
B树是一种多路平衡查找树,每个节点最多可以包含k个孩子,k为B树的阶(k的选择取决于磁盘页大小)
一个m阶的B树具有如下几个特征:
- 若根节点不是叶子节点则至少有两个子节点
- 每个中间节点都包含 k-1 个元素和 k 个孩子,其中 ⌈m/2⌉ <= k <= m
- 每个叶子节点都包含 k-1个元素,其中⌈m/2⌉ <= k <= m
- 所有的叶子节点都位于同一层
- 每个节点中的元素从小到大排列,节点当中k-1个元素刚好是k个孩子包含的元素的值域分划。
B-树主要应用于文件系统以及部分数据库索引,比如著名的非关系型数据库MongoDB,大部分关系型数据库比如Mysql则使用B+树作为索引。
B树的插入操作
参考博客
插入操作是指插入一条记录,即(key, value)的键值对。如果B树中已存在需要插入的键值对,则用需要插入的value替换旧的value。若B树不存在这个key,则一定是在叶子结点中进行插入操作。
1)根据要插入的key的值,找到叶子结点并插入。
2)判断当前结点key的个数是否小于等于m-1,若满足则结束,否则进行第3步。
3)以结点中间的key为中心分裂成左右两部分,然后将这个中间的key插入到父结点中,这个key的左子树指向分裂后的左半部分,这个key的右子支指向分裂后的右半部分,然后将当前结点指向父结点,继续进行第3步。( 当阶数m为偶数时,需要分裂时就不存在排序恰好在中间的key,那么我们选择中间位置的前一个key或中间位置的后一个key为中心进行分裂即可。 )
以5阶B树为例,介绍B树的插入操作,
在5阶B树中,结点最多有4个key,最少有2个key。
- 在空树中插入39
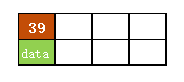
此时根结点就一个key,此时根结点也是叶子结点 - 继续插入22、97、41

根结点此时有4个key - 继续插入53

插入后超过了最大允许的关键字个数4,所以以key值为41为中心进行分裂,结果如下图所示,分裂后当前结点指针指向父结点,满足B树条件,插入操作结束。(当阶数m为偶数时,需要分裂时就不存在排序恰好在中间的key,那么我们选择中间位置的前一个key或中间位置的后一个key为中心进行分裂即可。)
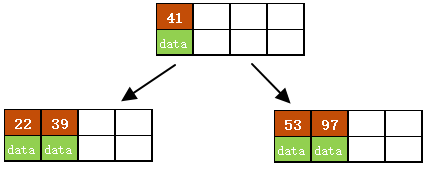
- 依次插入13、21、40
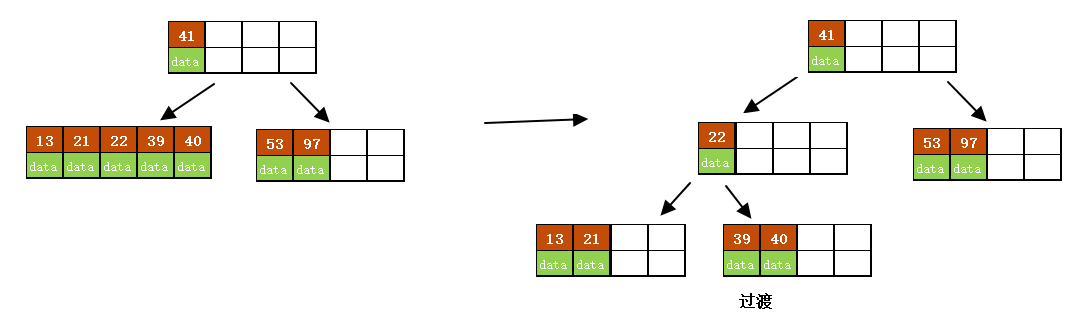
同样会造成分裂,结果如下图所示。
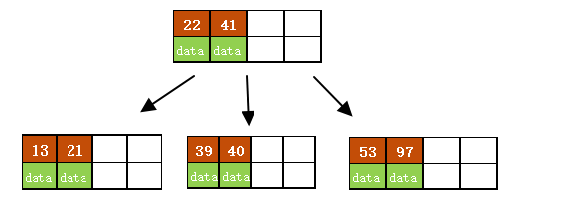
- 依次插入30、27、 33 ;36、35、34; 24、29
- 插入 30、27、 33
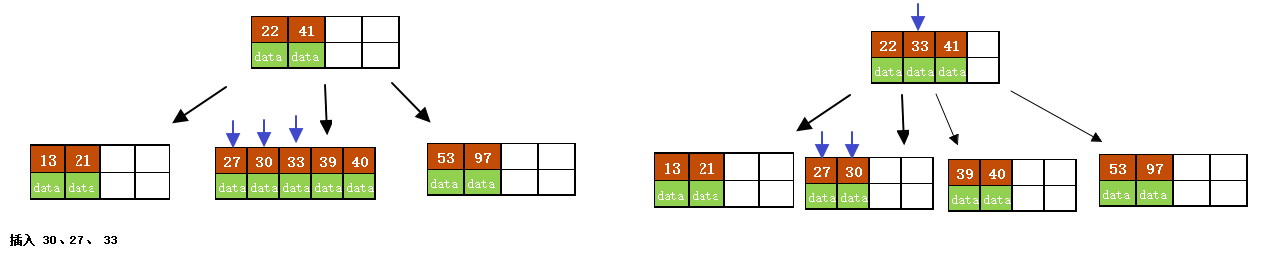
- 插入 36、35、34;
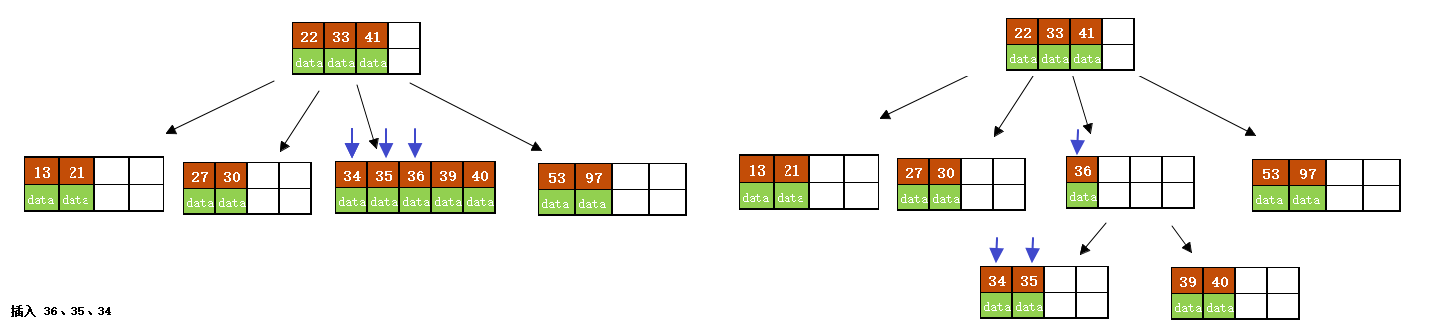
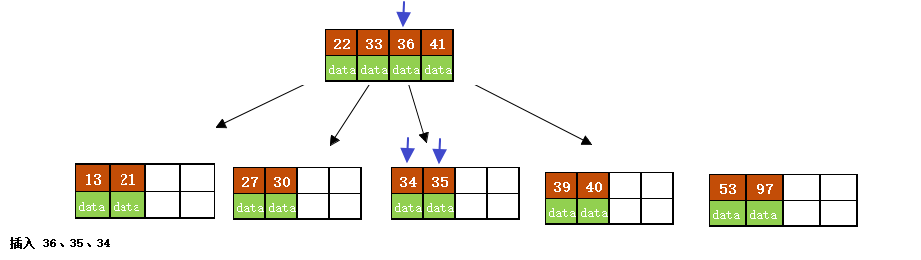
- 插入24、29
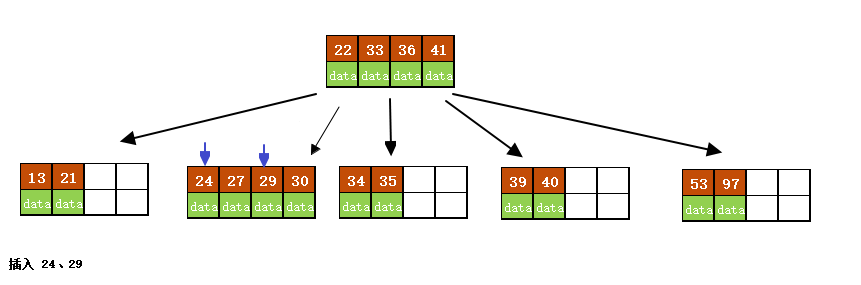
- 插入 30、27、 33
- 插入26
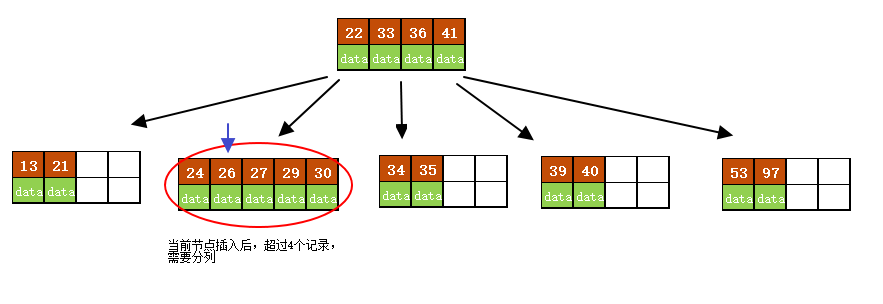
当前结点需要以27为中心分裂,并向父结点进位27,然后当前结点指向父结点,结果如下图所示。
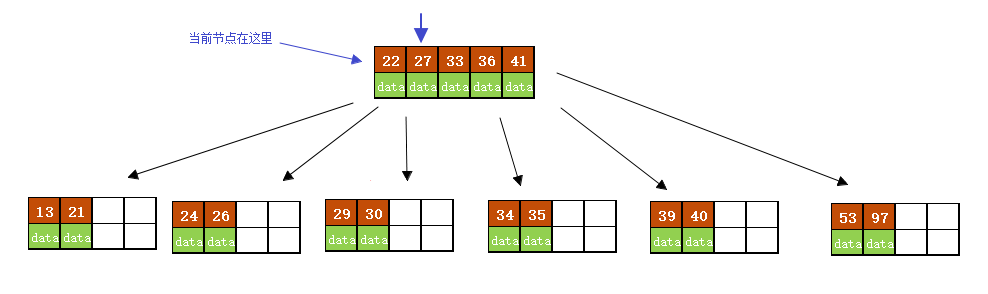
进位后导致当前结点(即根结点)也需要分裂,分裂的结果如下图所示。
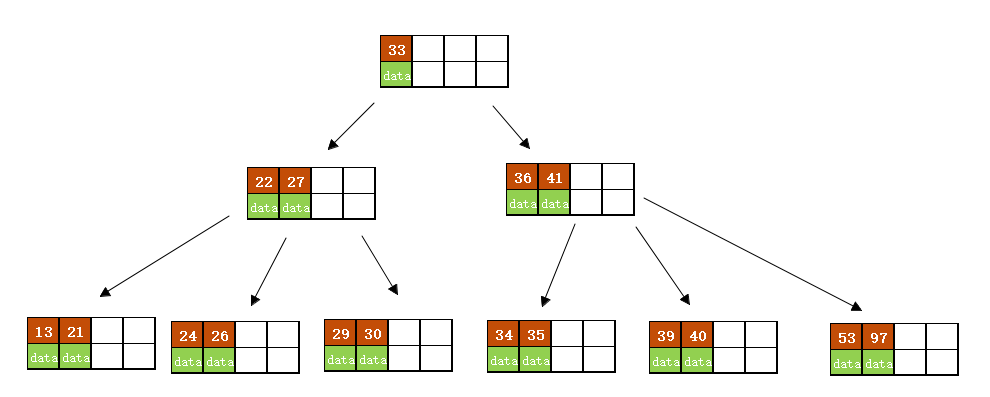
分裂后当前结点指向新的根,此时无需调整。 - 最后再依次插入key为 17、28、31、32 的记录
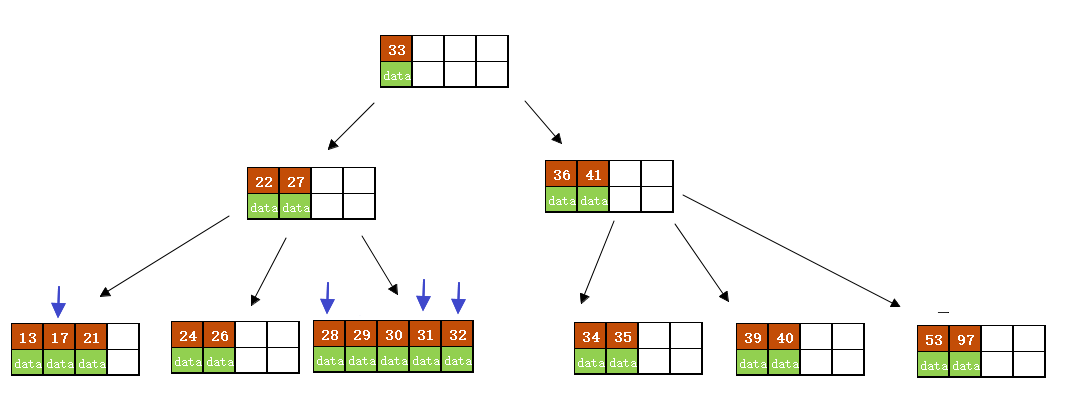
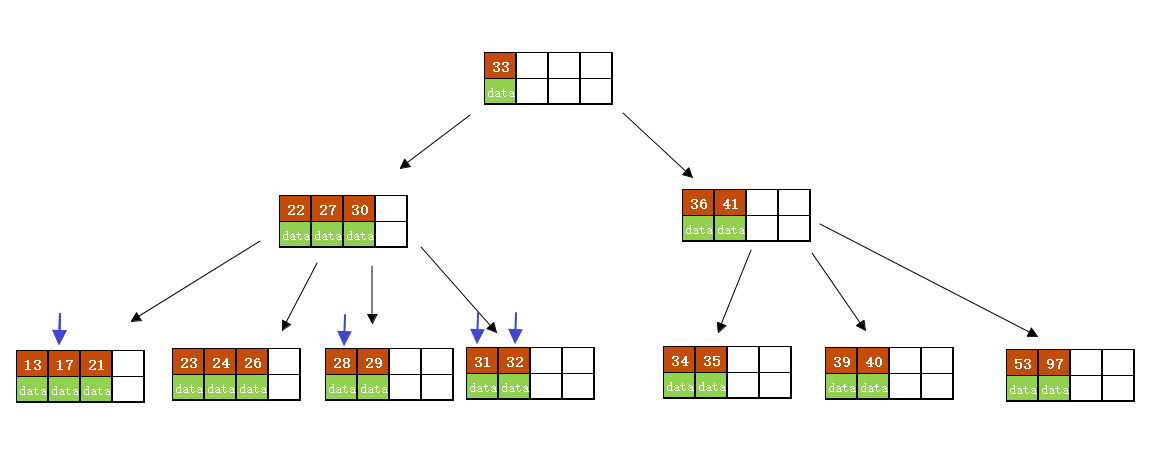
B树的删除操作
删除操作是指,根据key删除记录,如果B树中的记录中不存对应key的记录,则删除失败。
- 如果当前需要删除的key位于非叶子结点上,则用后继key(这里的后继key均指后继记录的意思)覆盖要删除的key,然后在后继key所在的子支中删除该后继key。此时后继key一定位于叶子结点上,这个过程和二叉搜索树删除结点的方式类似。删除这个记录后执行第2步
- 该结点key个数大于等于Math.ceil(m/2)-1,结束删除操作,否则执行第3步。
- 如果兄弟结点key个数大于Math.ceil(m/2)-1,则父结点中的key下移到该结点,兄弟结点中的一个key上移,删除操作结束。
否则,将父结点中的key下移与当前结点及它的兄弟结点中的key合并,形成一个新的结点。原父结点中的key的两个孩子指针就变成了一个孩子指针,指向这个新结点。然后当前结点的指针指向父结点,重复上第2步。
有些结点它可能即有左兄弟,又有右兄弟,那么我们任意选择一个兄弟结点进行操作即可。
以5阶B树为例,介绍B树的删除操作
5阶B树中,结点最多有4个key,最少有2个key
- 原始状态

- 在上面的B树中删除21,删除后结点中的关键字个数仍然大于等2,所以删除结束

- 在上述情况下接着删除27。从上图可知27位于非叶子结点中,所以用27的后继替换它。从图中可以看出,27的后继为28,我们用28替换27,然后在28(原27)的右孩子结点中删除28。删除后的结果如下图所示。
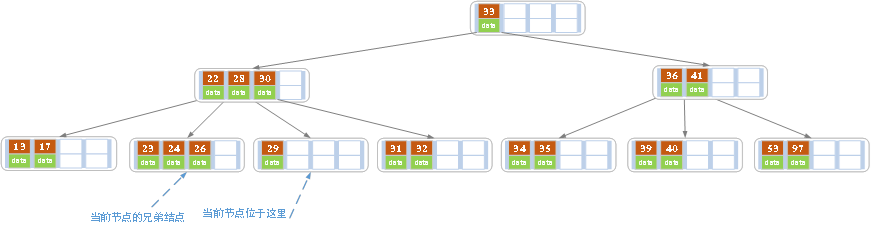
删除后发现,当前叶子结点的记录的个数小于2,而它的兄弟结点中有3个记录(当前结点还有一个右兄弟,选择右兄弟就会出现合并结点的情况,不论选哪一个都行,只是最后B树的形态会不一样而已),我们可以从兄弟结点中借取一个key。所以父结点中的28下移,兄弟结点中的26上移,删除结束。结果如下图所示。

- 在上述情况下接着删除32,结果如下图。
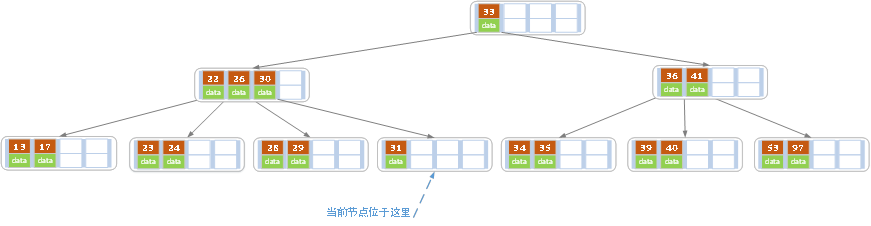
当删除后,当前结点中只有一个key,而兄弟结点中也仅有2个key。所以只能让父结点中的30下移和这个两个孩子结点中的key合并,成为一个新的结点,当前结点的指针指向父结点。结果如下图所示。
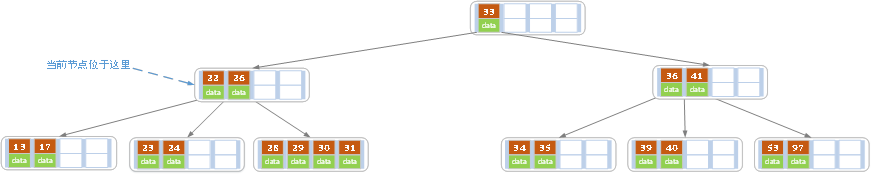
当前结点key的个数满足条件,故删除结束。 - 上述情况下,我们接着删除key为40的记录,删除后结果如下图所示。
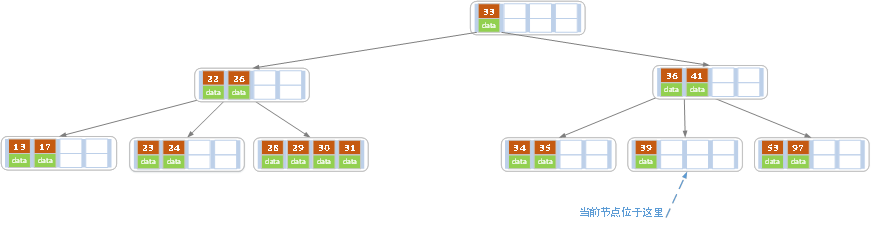
同理,当前结点的记录数小于2,兄弟结点中没有多余key,所以父结点中的key下移,和兄弟(这里我们选择左兄弟,选择右兄弟也可以)结点合并,合并后的指向当前结点的指针就指向了父结点。
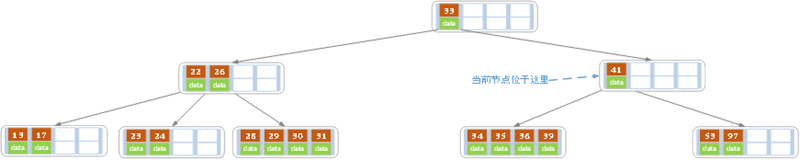
同理,对于当前结点而言只能继续合并了,最后结果如下所示。

合并后结点当前结点满足条件,删除结束。
B+树
参考文章
B+树是B-树的一种变体,有着比B-树更高的查询性能
一个m阶的B+树具有如下几个特征:
- 有k个子树的中间节点包含有k个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引,所有数据都保存在叶子节点。
- 所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
- 所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)的元素
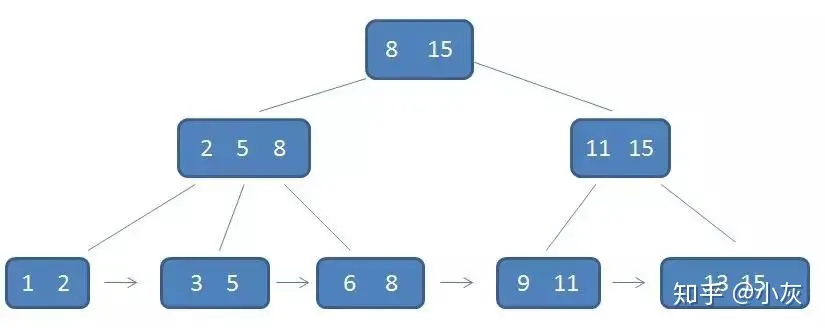
在B-树中无论是中间节点还是叶子节点都有卫星数据(牵引元素所指向的数据记录),而在B+树中只有叶子节点带有卫星数据,其余中间节点仅仅是索引,没有任何数据关联。
B+树的优点
-
单行查询
在单元素查询的时候,B+树会自顶向下逐层查找节点,最终找到匹配的叶子节点。步骤与B-树类似,但是B+树的中间节点没有卫星数据,所以同样大小的磁盘页可以容纳更多的节点元素,在数据量相同的情况下B+树比B-树更加“矮胖”查询IO的次数也更少。其次,B+树的查询必须最终查找到叶子节点,而B-树只要找到匹配元素即可,无论匹配元素处于中间节点还是叶子节点,因此B-树的查找性能不稳定(最好情况是根节点,最坏情况是叶子节点),而B+树的每次查找都是稳定的。 -
范围查询
B-树的范围查询只能依靠繁琐的中序遍历,B+树的范围查询只需要在链表上做遍历即可。
总结:
- 单一节点存储更多的元素,使得查询的IO次数更少。
- 所有查询都要查找到叶子节点,查询性能稳定。
- 所有叶子节点形成有序链表,便于范围查询。
红黑树
相关文章:

二叉搜索树、B-树、B+树
二叉搜索树 二叉查找树,也称为二叉搜索树、有序二叉树或排序二叉树,是指一棵空树或者具有下列性质的二叉树: 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;若任意节点的右子树不空࿰…...
Docker简介与安装
简介 用来快速构建、运行、管理应用的工具简单说,帮助我们部署项目以及项目所依赖的各种组件典型的运维工具 安装 1.卸载旧版 首先如果系统中已经存在旧的Docker,则先卸载: yum remove docker \docker-client \docker-client-latest \dock…...

Swift 单元测试
Swift 单元测试是用于检查代码的正确性和稳定性的一种测试方法。它可以帮助开发者在编写代码时及时发现和解决错误,提高代码质量。 在 Swift 中,可以使用 XCTest 框架来编写和运行单元测试。以下是一个简单的示例: import XCTestclass MyMa…...

有来团队后台项目-解析10
axios 安装 pnpm i axios创建文件 src 目录下创建 utils 文件夹,utils 文件夹下创建request.ts src 目录下创建store 文件夹,文件夹下创建index.ts ,创建modules 文件夹 编写request.ts // 引入axios,引入请求拦截器类型约束…...

【自动化】在C#中创建和配置串口对象SerialPort
串口通信在各种应用场景中都有广泛的应用,如工业控制、数据采集等。在.NET框架中,SerialPort类是用于串口通信的一个非常实用的类。本文将介绍如何在C#中使用SerialPort类进行串口通信,包括SerialPort的创建方法、基本属性设置和数据发送的基…...
)
突破编程_C++_设计模式(访问者模式)
1 访问者模式的基本概念 C中的访问者模式是一种行为设计模式,它允许你在不修改类层次结构的情况下增加新的操作。这种模式将数据结构与数据操作解耦,使得操作可以独立于对象的类来定义。 访问者模式的主要组成部分包括: (1&…...
)
C语言入门到精通之练习53:矩阵交换行问题(附带源码)
描述 给定一个 5*5 的矩阵(数学上,一个 rc 的矩阵是一个由 r 行 c 列元素排列成的矩形阵列),将第 n 行和第 m 行交换,输出交换后的结果。 输入输入共 6 行,前 5 行为矩阵的每一行元素, 元素与元素之间以一…...

Python白练-2统计下列5行字符串中字符出现的频数
问题:统计下列5行字符串中字符a、c、g、t出现的频数 数据:data2_2: 1.aggcacggaaaaacgggaataacggaggaggacttggcacggcattacacggagg 2.cggaggacaaacgggatggcggtattggaggtggcggactgttcgggga 3.gggacggatacggattctggccacggacggaaaggaggacacggcg…...

深入理解DHCP服务:网络地址的自动化分配
深入理解DHCP服务:网络地址的自动化分配 在现代网络环境中,动态主机配置协议(DHCP) 是一个至关重要的服务,它允许自动分配IP地址和其他相关配置信息给网络中的设备。本文将深入探讨DHCP服务的工作原理、配置方法以及如…...

Java高级编程—泛型
文章目录 1.为什么要有泛型 (Generic)1.1 泛型的概念1.2 使用泛型后的好处 2.在集合中使用泛型3.自定义泛型结构3.1 自定义泛型类、泛型接口3.2 自定义泛型方法 4.泛型在继承上的体现5.通配符的使用5.1 基本使用5.2 有限制的通配符的使用 1.为什么要有泛型 (Generic) Java中的…...

Exam in MAC [容斥]
题意 思路 正难则反 反过来需要考虑的是: (1) 所有满条件一的(x,y)有多少对: x 0 时,有c1对 x 1 时,有c对 ...... x c 时,有1对 以此类推 一共有 (c2)(c1)/2 对 (2) 符合 x y ∈ S的有多少对:…...

Java 学习和实践笔记(36):接口(interface)
面向对象的精髓,最能体现这一点的就是接口! 为什么我们讨论设计模式都只针对具备了抽象能力的语言(比如C、Java、C#等),就是因为设计模式所研究的,实际上就是如何合理的去抽象。 接口就是一组规范,所有实…...

Elastic Stack--10--QueryBuilders UpdateQuery
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 QueryBuildersESUtil QueryBuilders package com.elasticsearch; import org.elasticsearch.action.ActionListener; import org.elasticsearch.action.search.Sea…...

腾讯云服务器CVM_云主机_云计算服务器_弹性云服务器
腾讯云服务器CVM提供安全可靠的弹性计算服务,腾讯云明星级云服务器,弹性计算实时扩展或缩减计算资源,支持包年包月、按量计费和竞价实例计费模式,CVM提供多种CPU、内存、硬盘和带宽可以灵活调整的实例规格,提供9个9的数…...

Java八股文(Spring Boot)
Java八股文のSpring Boot Spring Boot Spring Boot 什么是Spring Boot? Spring Boot是一个用于开发和构建微服务应用程序的框架,它简化了Spring应用的配置和部署。 Spring Boot的核心特性是什么? Spring Boot的核心特性包括自动配置、起步依…...

ts文件怎么无损转换mp4?这样设置转换模式~
TS格式(Transport Stream)的起源可追溯到数字电视广播领域。设计初衷是解决视频、音频等多媒体数据在传输和存储中的问题。采用一系列标准技术,TS格式让视频信号能够以流的形式传输,因此在数字电视、广播等领域得到广泛应用。 MP4…...
如何在Windows 10上打开和关闭平板模式?这里提供详细步骤
前言 默认情况下,当你将可翻转PC重新配置为平板模式时,Windows 10会自动切换到平板模式。如果你希望手动打开或关闭平板模式,有几种方法可以实现。 自动平板模式在Windows 10上如何工作 如果你使用的是二合一可翻转笔记本电脑࿰…...

介绍kafka核心原理及底层刷盘机制,集群分片机制,消息丢失和重复消费有对应的线上解决方案
Kafka是一个高性能、分布式、持久化的消息系统,它的核心原理包括发布/订阅模型、分布式日志存储和高吞吐量的数据流处理。 发布/订阅模型:Kafka采用发布/订阅模型,消息的生产者将消息发送到一个或多个主题(Topic)&…...
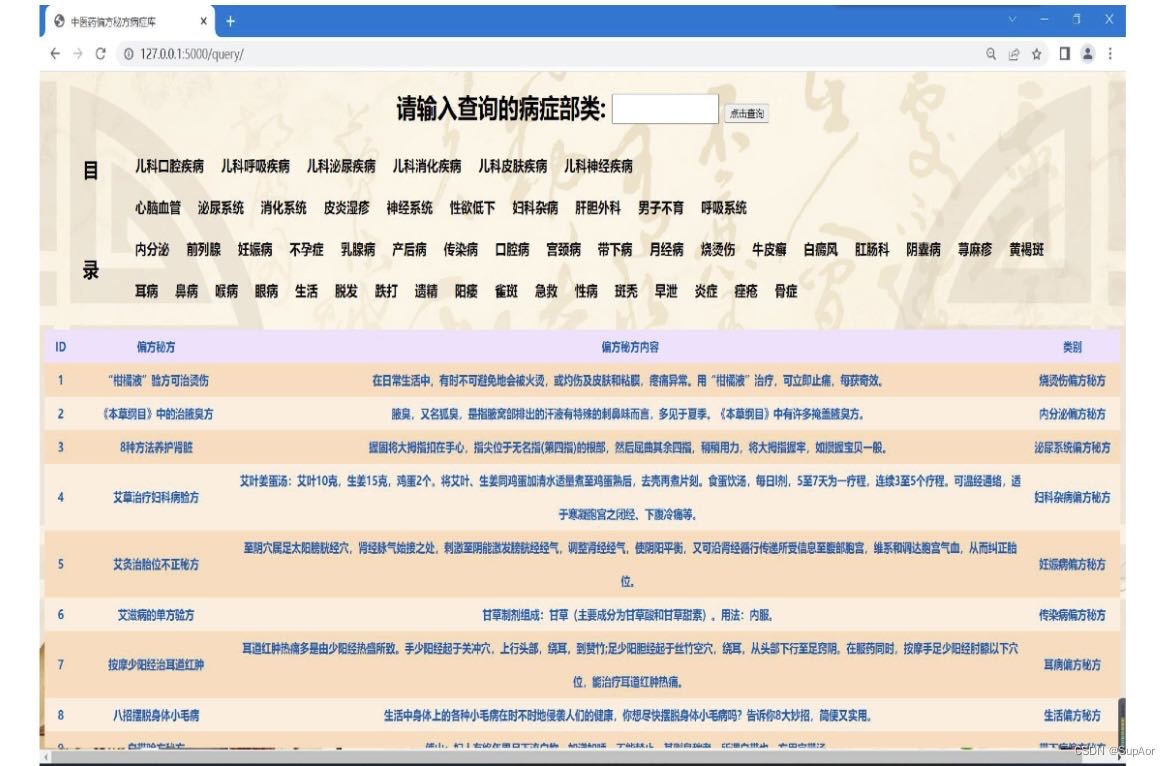
基于Python的中医药知识问答系统设计与实现
[简介] 这篇文章主要介绍了基于Python的中医药知识问答系统的设计与实现。该系统利用Python编程语言,结合中医药领域的知识和技术,实现了一个功能强大的问答系统。文章首先介绍了中医药知识的特点和传统问答系统的局限性,然后提出了设计思路…...

QT 如何防止 QTextEdit 自动滚动到最下方
在往QTextEdit里面append字符串时,如果超出其高度,默认会自动滚动到QTextEdit最下方。但是有些场景可能想从文本最开始的地方展示,那么就需要禁止自动滚动。 我们可以在append之后,添加如下代码: //设置编辑框的光标位…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
