蓝桥杯深度优先搜索|剪枝|N皇后问题|路径之谜(C++)
搜索:暴力法算法思想的具体实现
搜索:通用的方法,一个问题如果比较难,那么先尝试一下搜索,或许能启发出更好的算法
技巧:竞赛时遇到不会的难题,用搜索提交一下,说不定部分判题数据很弱,得分了
暴力法
把所有的可能性都列举出来,一一验证,简单直接
利用计算机强大的计算能力和存储能力
依赖的是递归
深度优先搜索
Depth First Search 即 DFS,意为深度优先搜索,是所有的搜索手段之一。它是从某个状态开始,不断进行状态转移,直到不能转移后,向后回退,一直到遍历完所有的状态。
深度优先搜索基本概念
作为搜索算法的一种,DFS 主要是用于解决 NP 完全问题。但是,深度优先搜索算法的时间复杂度较高,深度优先搜索是 O ( n ! ) O(n!) O(n!) 的阶乘级算法,它的效率非常低,在数据规模变大时,此算法就难以解决当前的问题了。
所以搜索算法使用于状态节点较小规模的问题。
DFS 的设计步骤
按照定义设计:
- 确定该题目的状态(包括边界)
- 找到状态转移方式
- 找到问题的出口,计数或者某个状态
- 设计搜索
DFS基础:递归和记忆化搜索
形式上,递归函数是自己调用自己,是一个不断重复的过程
递归的思想是把大问题逐步缩小,直到变成最小的同类问题的过程,而最后的小问题的解是已知的,一般是给定的初始条件
到达最小问题之后,再回溯,把小问题的解逐个带回给更大的问题,最终大问题也得到了解决
递归有两个过程:递归前进、递归返回
在递归过程中,由于大问题和小问题的解决方法完全一样,那么大问题的代码和小问题的代码可以写成一样
一个递归函数,直接调用自己,实现了程序的复用
DFS的代码框架
ans //答案,用全局变量表示
def dfs (层数 (状态), 其他参数):if (条件判断) //到达最底层(达到最终状态),或者满足条件退出更新答案 //答案一般用全局变量表示return //返回到上一层剪枝 //在进一步DFS之前剪枝for (枚举下一层可能的情况)://对每一个情况继续DFSif (used[i] == 0): //如果状态i没有用过,就可以进入下一层used[i] = 1 //称为保存现场,占有现场//标记状态i,表示已经用过,在更底层不能再使用dfs(层数+1, 其他参数) //下一层used[i] = 0 //称为恢复现场,释放现场//恢复状态,回溯时,不影响上一层对这个状态的使用return //返回到上一层
剪枝
题目中给了要求是y<30
当扩展到y=29这个点以后,就不需要继续往后扩展了
伪代码:
int check(参数)
{if(满足条件)return 1;return 0;
}
bool pd(参数){相应操作
}
void dfs(int step)
{判断边界pd(){不在边界内,即回溯}尝试每一种可能{满足check条件标记继续下一步dfs(step+1)恢复初始状态(回溯的时候要用到)}
}
DFS:剪枝
剪枝:把不会产生答案的,或不必要的枝条剪掉
剪枝的关键:剪什么枝、在哪里剪
剪枝是搜索常用的优化手段,常常能把指数级的复杂度,优化到近似多项式的复杂度
可行性剪枝:对当前状态进行检查,如果当前条件不合法就不再继续,直接返回
搜索顺序剪枝:搜索树有多个层次和分支,不同的搜索顺序会产生不同的搜索树形态
最优性剪枝:在最优化问题的搜索过程中,如果当前花费的代价已超过前面搜索到的最优解,那么本次搜索已经没有继续进行下去的意义,停止对当前分支的搜索
排除等效冗余:搜索不同的分支,最后的结果是一样的,那么只搜一个分支就够了
记忆化搜索:在递归的过程中,有许多分支被反复计算,会大大降低算法执行的效率。将已经计算出来的结果保存起来,以后需要用到的时候直接取出结果,避免重复运算,从而提高了算法的效率
DFS 题目讲解
1. 状态搜索代表: N 皇后问题
题目链接
难度: 简单
标签: DFS
题目描述:
在N×N的方格棋盘放置了N 个皇后,使得它们不相互攻击(即任意 22 个皇后不允许处在同一排,同一列,也不允许处在与棋盘边框成 45 角的斜线上。你的任务是,对于给定的N,求出有多少种合法的放置方法。
输入描述:
输入中有一个正整数 N≤10,表示棋盘和皇后的数量
输出描述:
为一个正整数,表示对应输入行的皇后的不同放置数量。
输入输出样例:
示例:
输入:
5
输出:
10
运行限制:
最大运行时间:1s最大运行内存: 256M
解题思路:
二维搜索问题,有一个x坐标一个y坐标
下面是用递归的深度优先搜索求解 n 皇后问题的算法描述:
这里用一个 N×N 的矩阵来表示棋盘,但是我们不需要定义这样的数组,只要心中有 N×N 的棋盘即可。
- 算法开始:
当前行设为第一行,当前列设为第一列,从第一行第一列开始搜索,即只能让皇后从第一行放到第 n 行。
这样在每次判断是否满足情况时我们不用去判断是否皇后在相同行。
我们只用判断之前的 1 到 a−1 个皇后的位置和当前第 a 个皇后的位置是否属于同一列或者斜线,判断是否同一列。 - 判断边界:
在当前行,当前列的位置上判断是否满足条件(即保证经过这一点的行,列与斜线上都没有两个皇后),若不满足,跳到第 5 步,即不符合边界条件。
首先说一下,什么叫不符合边界条件,不只是跳出了搜索范围,剪枝也可以从这里开始,比如这里不满足条件,向下继续搜索也不会再有结果。
这可以理解为超出边界的剪枝,我们的边界只得可能存在解的范围,这里已经超出有解的范围,必然要被踢出。
判断条件:
我们用数组 x [ a ] = i x[a]=i x[a]=i 来表示第 a 个皇后的位置在第 a 行第 i 列,我们不用考虑是否在同一行的问题你,我们只用判断之前的 1 到 a−1 个皇后的位置和当前第 a 个皇后的位置是否属于同一列或者斜线。
判断是否属于同一列: 就判断 x [ a ] x[a] x[a] 是否等于 x [ i ] x[i] x[i]; 判断是否属于同一斜线:等同于判断行之差是否等于列之差也,即 a b s ( x [ k ] − x [ i ] ) ≠ a b s ( k − i ) x [ k ] ≠ x [ i ] \begin{array}{} abs(x[k]−x[i])\ne abs(k−i)\\ x[k]\ne x[i] \end{array} abs(x[k]−x[i])=abs(k−i)x[k]=x[i] - 搜索过程:
调用Check函数。
如果 边界条件,就继续调用放下一个皇后的位置 Check函数:
如果当搜索到第 N+1 行的时候,即代表前 N 行已经搜索完了,所以这个时候正好求出了一个解,记录加一。- 在当前位置上不满足条件的情形,进行回溯
搜索过程
![![[Pasted image 20240310171129.png]]](https://img-blog.csdnimg.cn/direct/5d957d90fa2c4eb1b1d48162b08f9f7b.png)
回溯,把放过的收起来
不是直接回溯到最开始,而是从第五行开始往第一行走,一层一层回溯,回到之前的每一行,继续往下一列走,判断有没有新的解,没有的话,就继续往前回溯
![![[Pasted image 20240310171558.png]]](https://img-blog.csdnimg.cn/direct/ef2174d22b0c4273b83c32324e73695c.png)
回溯到第二行,找到新的解,停止回溯,往后搜索,寻找新的解
![![[Pasted image 20240310171716.png]]](https://img-blog.csdnimg.cn/direct/c5e0544dfb3946faa883db5ddb2697fa.png)
找到新的解,ans+1,第五行没有别的解了,往前回溯
代码
C++ 语言描述:
占用的代码
#include <iostream>
#include <cstdio>
using namespace std;
int x[15] = {0}; //已知N小于10,建15没有问题
int sum,n;//判断是不是在同一列或者同一斜线上
int PD(int k)
{for(int i=1; i<k; i++){if(abs(k-i)==abs(x[k]-x[i]))return 0;else if (x[k]==x[i])return 0;//即判断是否符合条件来放,i表示皇后所在的行数,x[i]表示所在的列数,//所以前面那个条件用来判断两个皇后是否在对角线上,后面用来判断是否在同一列上。//行数不需要判断,因为他们本身的i就代表的是行数}return 1;
}bool check(int a)
{if(a>n) //当放到n+1的时候,代表前n个已经放好了sum++; //前面的放好了,ans+1elsereturn 0;return 1;
}void DFS(int a)
{if(check(a)) //判断是不是走到第n+1层,找到a了,直接返回return ;else //如果没找到,继续往下找for(int i=1; i<=n; i++) //从这一行的第一个往后放{if (x[a] != 0) //当前位置已被放过continue;x[a]=i; //第a个皇后放的列数,标记使用if(PD(a)) //判断是否能放这步DFS(a+1);//能的话进行下一个皇后的放置x[a] = 0;//释放现场//不能就下一列}
}
int main()
{cin>>n;//表示几个皇后DFS(1);//每次都从第一个皇后开始cout<<sum<<endl;return 0;
}
不占用的代码
#include <iostream>
#include <cstdio>
using namespace std;
int x[15] = {0};
int sum,n;int PD(int k)
{for(int i=1; i<k; i++){if(abs(k-i)==abs(x[k]-x[i]))return 0;else if (x[k]==x[i])return 0;//即判断是否符合条件来放,i表示皇后所在的行数,x[i]表示所在的列数,//所以前面那个条件用来判断两个皇后是否在对角线上,后面用来判断是否在同一列上。//行数不需要判断,因为他们本身的i就代表的是行数}return 1;
}bool check(int a)
{if(a>n)sum++;elsereturn 0;return 1;
}void DFS(int a)
{if(check(a))return ;elsefor(int i=1; i<=n; i++){x[a]=i;//第a个皇后放的列数if(PD(a))//判断是否能放这步DFS(a+1);//能的话进行下一个皇后的放置else continue ;//不能就下一列}
}
int main()
{cin>>n;//表示几个皇后DFS(1);//每次都从第一个皇后开始cout<<sum<<endl;return 0;
}
2. 图的路径搜索代表-路径之谜
题目链接
难度: 中等
标签: DFS, 2016, 国赛
题目描述:
小明冒充 X 星球的骑士,进入了一个奇怪的城堡。
城堡里边什么都没有,只有方形石头铺成的地面。
假设城堡地面是 n×n 个方格。如下图所示。
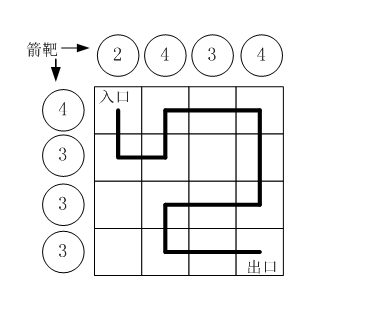
按习俗,骑士要从西北角走到东南角。可以横向或纵向移动,但不能斜着走,也不能跳跃。每走到一个新方格,就要向正北方和正西方各射一箭。(城堡的西墙和北墙内各有 n 个靶子)同一个方格只允许经过一次。但不必走完所有的方格。如果只给出靶子上箭的数目,你能推断出骑士的行走路线吗?有时是可以的,比如上图中的例子。
本题的要求就是已知箭靶数字,求骑士的行走路径(测试数据保证路径唯一)
输入:
第一行一个整数 N (0≤N≤20),表示地面有 N×N 个方格。
第二行 N 个整数,空格分开,表示北边的箭靶上的数字(自西向东)
第三行 N 个整数,空格分开,表示西边的箭靶上的数字(自北向南)
输出:
输出一行若干个整数,表示骑士路径。
为了方便表示,我们约定每个小格子用一个数字代表,从西北角开始编号: 0,1,2,3 ⋯⋯
输入输出样例:
输入
4
2 4 3 4
4 3 3 3
比如,上图中的方块编号为:
| 箭靶 | 2 | 4 | 3 | 4 |
|---|---|---|---|---|
| 4 | 0 | 1 | 2 | 3 |
| 3 | 4 | 5 | 6 | 7 |
| 3 | 8 | 9 | 10 | 11 |
| 3 | 12 | 13 | 14 | 15 |
输出
0 4 5 1 2 3 7 11 10 9 13 14 15
运行限制:
最大运行时间:1s
最大运行内存: 128M
解题思路:
这里用一个 N×N 的矩阵来表示城堡的位置,横向、纵向标号 1−N。
我们采用逆推法,既然原题目是走到哪里射一支箭,那我们就走到那里之后拔一支箭,如果最后得到所有的靶子上都没有箭了,由于题目的路径唯一,那就证明我们找到了题目所要求的路径。
- 算法开始:
当前行设为第一行,当前列设为第一列,从第一行第一列开始搜索。
然后从左上角初始位置,按照题目意思进行寻路。 - 判断边界:
在当前行,当前列的位置上判断是否满足条件,若不满足,跳到第 5 步,即不符合边界条件。 判断条件如下:- f l a g [ x ] [ y ] = = 1 flag[x][y]==1 flag[x][y]==1 标记数组已经被标记,已被走过,不能再走,超出边界
- x < 1 x<1 x<1 从左侧走出方格。
- x > n x>n x>n 从右侧走出方格。
- y < 1 y<1 y<1 从上侧走出方格。
- y > n y>n y>n 从下侧走出方格。
- c o l [ x ] < = 0 col[x]<=0 col[x]<=0 没走到右下角,箭用完了。
- r o l [ y ] < = 0 rol[y]<=0 rol[y]<=0 没走到右下角,箭用完了
- 搜索过程:
调用Check函数。 如果边界条件满足,就继续调用搜索,找到下一步的位置 - check(参数):
如果当搜索到 x = n , y = n x=n,y=n x=n,y=n 时,且靶子上的箭都没了,按就找到了答案。
按照题目输出即可。 - 在当前位置上不满足条件的情形,进行回溯,并还原现场
C++ 语言描述:
#include <bits/stdc++.h>using namespace std;struct PII
{int first;int second;
};const int N = 30;
int rol[N];
int col[N];
int n;//格子数 长宽从1到n
bool flag[N][N]; //用来标记是否走过
vector<PII> res;//---------图的路径搜索常用方向移动表示-------int dx[4]= {0,1,-1,0};
int dy[4]= {1,0,0,-1};// 两两组合形成上下左右四个方向
// 1------------------> x
// |
// |
// |
// |
// |
// |
// |
// ↓
// y// dx[0]=0 dy[0]=1 那么代表向下的方向
// dx[1]=1 dy[1]=0 那么代表向右的方向
// dx[2]=-1 dy[2]=0 那么代表向左的方向
// dx[3]=0 dy[3]=-1 那么代表向上的方向//--------------------------------------------bool check(int x, int y) //判断走过的路径的箭靶数是否与目标相同
{if(x==n && y==n) //表示走到右下角了{for(int i=1; i<=n; i++) //从1~n开始判断北边的靶子有没有箭{if(col[i]!=0){return false;}//如果箭靶上的数目不为0,根据逆推,我们通过当前路径得不到箭靶上的结果}for(int i=1; i<=n; i++) //判断西边的靶子上有没有箭{if(rol[i]!=0){return false;}//如果箭靶上的数目不为0,根据逆推,我们通过当前路径得不到箭靶上的结果}for(int i=0; i<res.size(); i++) //如果有,把答案进行输出{int x=res[i].first;//x 轴坐标int y=res[i].second;//y 轴坐标int sum=n*(x-1)+y-1 ;// 通过计算的到为题目要求的坐标系cout <<sum<< " ";}cout << endl;return false;// 成功终止}return true; //继续搜索//关于终止还是继续我们交给判定即可
}
bool pd(int x2,int y2) //边界判断
{if(flag[x2][y2]==1)return 0;//已被走过,不能再走,超出边界else if(x2<1)return 0;//从左侧走出方格else if(x2>n)return 0;//从右侧走出方格else if(y2<1)return 0;//从上侧走出方格else if(y2>n)return 0;//从下侧走出方格else if(col[x2]<=0)return 0;//没走到右下角,箭用完了else if(rol[y2]<=0)return 0;//没走到右下角,箭用完了else return 1;//符合边界条件,可以继续执行搜索
}void dfs(int x,int y)
{if(!check(x,y)) //判断是不是符合规则{return ;//包含不符合规则的地方,回溯,用于剪枝}else //如果符合规则,就扩展{for(int i=0; i<4; i++){int xt=dx[i]+x; //完成上下左右四个方向的移动int yt=dy[i]+y;if(!pd(xt,yt)){continue ;//不符合要求继续换方向搜索}else{//因为要进行位置转移,我们给它起个名字,叫作案现场//比如向下移动flag[xt][yt]=true; //搜索到这个点,把它标记起来col[xt]--; //北边拔一个箭rol[yt]--; //西边拔一个箭res.push_back({xt,yt}); //把每次路径的点放入vector//继续向下搜索dfs(xt,yt);//搜索回溯后,因为没有找到正确答案,所以要回复作案现场,返回到搜索之前res.pop_back();flag[xt][yt]=false;col[xt]++;rol[yt]++;}}}
}int main()
{cin >> n;for(int i=1; i<=n; i++)cin >> rol[i];for(int i=1; i<=n; i++)cin >> col[i];flag[1][1]=true;col[1]--;rol[1]--;res.push_back({1,1});dfs(1,1);return 0;
}
相关文章:

蓝桥杯深度优先搜索|剪枝|N皇后问题|路径之谜(C++)
搜索:暴力法算法思想的具体实现 搜索:通用的方法,一个问题如果比较难,那么先尝试一下搜索,或许能启发出更好的算法 技巧:竞赛时遇到不会的难题,用搜索提交一下,说不定部分判题数据很…...

大门对楼梯,怎么办?
中国是一个非常重视风水的国家,风水学发扬和流传已有几千年的历史,很多懂风水的人都知道,大门风水是其中非常重要的一环,因为大门风水直接影响全家人的各种运势。大门风水好,能帮助你一臂之力;若大门风…...

解决驱动开发中<stdlib.h> no such file 的问题
前言 在进行驱动开发时,需要使用malloc等函数,导入C库<stdlib.h>出现bug。 嵌入式驱动学习专栏将详细记录博主学习驱动的详细过程,未来预计四个月将高强度更新本专栏,喜欢的可以关注本博主并订阅本专栏,一起讨论…...

Find My工牌|苹果Find My技术与工牌结合,智能防丢,全球定位
工作牌一般是由公司发行的,带有相关工作号及佩戴人信息的卡牌,一般由塑料制作而成。具有醒目.增强内部员工归属感等作用。主要构成为公司名字背景图片员工名字照片。胸牌是一种悬挂或串扣于上衣左方的一种工号牌或介绍小标牌,大多数佩戴在西装…...

Springboot解决跨域问题
跨域问题 在Spring Boot中解决跨域问题的原因是因为浏览器的同源策略(Same-Origin Policy)限制了从一个源加载的文档或脚本如何与来自另一个源的资源进行交互。如果前端页面和后端服务不在同一个源(域名、协议、端口号都不相同)&…...

UE5 C++ TPS开发 学习记录(10
p22 这节课把创建,查找,加入游戏房间的菜单类,以及插件内的系统类给补完了.说实话这节课有点绕,因为需要一直使用委托进行传值,先由菜单类Menu向系统类Subsystem发送函数传值请求,然后监听Subsystem的委托回调,同时系统类Subsystem向Session的工具发送请求,监听回调,再返回给M…...

ES6(一):let和const、模板字符串、函数默认值、剩余参数、扩展运算符、箭头函数
一、let和const声明变量 1.let没有变量提升,把let放下面打印不出来,放上面可以 <script>console.log(a);let a1;</script> 2.let是一个块级作用域,花括号里面声明的变量外面找不到 <script>console.log(b);if(true){let b1;}//und…...

Docker使用及部署流程
文章目录 1. 准备Docker环境2. 准备应用的Docker镜像3. 在服务器上运行Docker容器方法一:Docker Hub方法二:从构建环境传输镜像4. 管理和维护使用Docker Compose(可选)主要区别步骤 1: 安装Docker ComposeLinuxWindowMac步骤 2: 创建docker-compose.yml文件步骤 3: 使用Doc…...
Nginx的日志怎么看,在哪看,access.log日志内容详解
Nginx 的日志文件通常位于服务器的文件系统中,具体位置可能因配置而异。以下是查看 Nginx 日志的几种方法: 1、查看访问日志:在默认配置下,Nginx 的访问日志文件路径为 /var/log/nginx/access.log。您可以通过命令 sudo cat /var…...
Windows Server 各版本搭建终端服务器实现远程访问(03~19)
一、Windows Server 2003 左下角开始➡管理工具➡管理您的服务器,点击添加或删除角色 点击下一步 勾选自定义,点击下一步 点击终端服务器,点击下一步 点击确定 重新登录后点击确定 点击开始➡管理工具➡计算机管理,展开本地用户…...
Node.js入门基础—day01
个人名片: 😊作者简介:一名大二在校生 🤡 个人主页:坠入暮云间x 🐼座右铭:给自己一个梦想,给世界一个惊喜。 🎅**学习目标: 坚持每一次的学习打卡 文章目录 初识node.js什…...

基于FPGA的PSRAM接口设计与实现
该系列为神经网络硬件加速器应用中涉及的模块接口部分,随手记录,以免时间久了遗忘。 一 PSRAM与HyperRAM 1、概述 2、异同 接口协议不同,因此在IP设计时需要注意。 Hyperram(Winbond):HyperBus协议 PSRAM(AP公司):X…...

OpenCV 图像的几何变换
一、图像缩放 1.API cv2.resize(src, dsize, fx0,fy0,interpolation cv2.INTER_LINEAR) 参数: ①src :输入图像 ②dsize:绝对尺寸 ③fx,fy:相对尺寸 ④interpolation:插值方法 2.代码演示 import cv2 …...
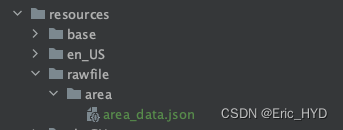
鸿蒙 - 读取 rawfile 中的 json 文件
一、说明 在以下目录中存放了一份地区 json 文件。 我想要将其读出来,并且转为我的实体类。 二、技术实现 import common from ohos.app.ability.common import { CityEntity } from ./entity/CityEntity import util from ohos.util;/*** App 内置的地区数据* r…...

【Stable Diffusion】入门-02:AI绘画提示词+参数设置攻略
目录 1 提示词1.1 分类和书写方式1.1.1 内容型提示词1.1.2 标准化提示词1.1.3 通用模板 1.2 权重1.2.1 套括号1.2.2 数字权重1.2.3 进阶语法 1.3 负面提示词 2 参数详解2.1 Sampling steps2.2 Sampling method2.3 Width, Height2.4 CFG Scale2.5 Seed2.6 Batch count, Batch si…...

Spring Boot启动时执行初始化操作的几种方式
场景 项目中,经常需要在启动过程中初始化一些数据,如从数据库读取一些配置初始化,或从数据库读取一些热点数据到redis进行初始化缓存。 方式一:实现CommandLineRunner 接口重写run方法逻辑 CommandLineRunner是Spring提供的接口࿰…...
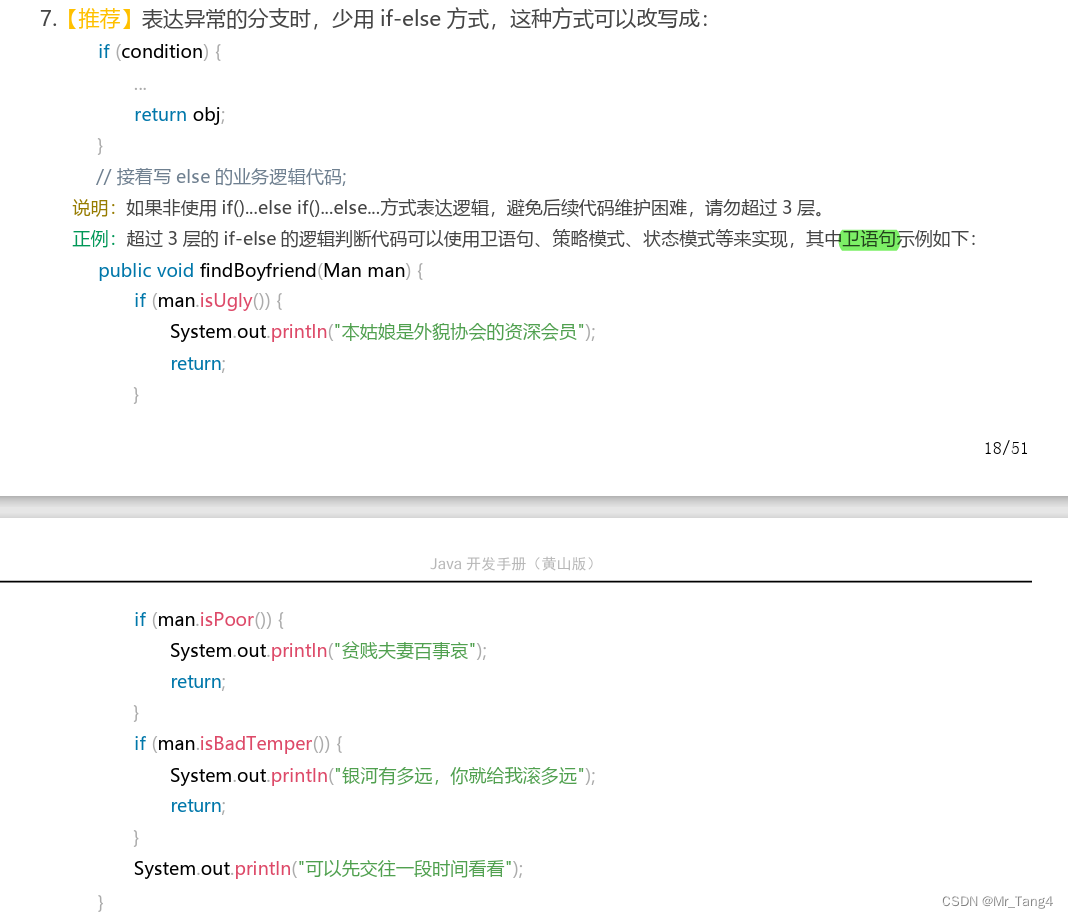
考研失败, 学点Java打小工——Day3
1 编码规范——卫语句 表达异常分支时,少用if-else方式。 比如成绩判断中对于非法输入的处理: /*>90 <100 优秀>80 <90 良好>70 <80 一般>60 <70 及格<60 不及格*/Testpu…...
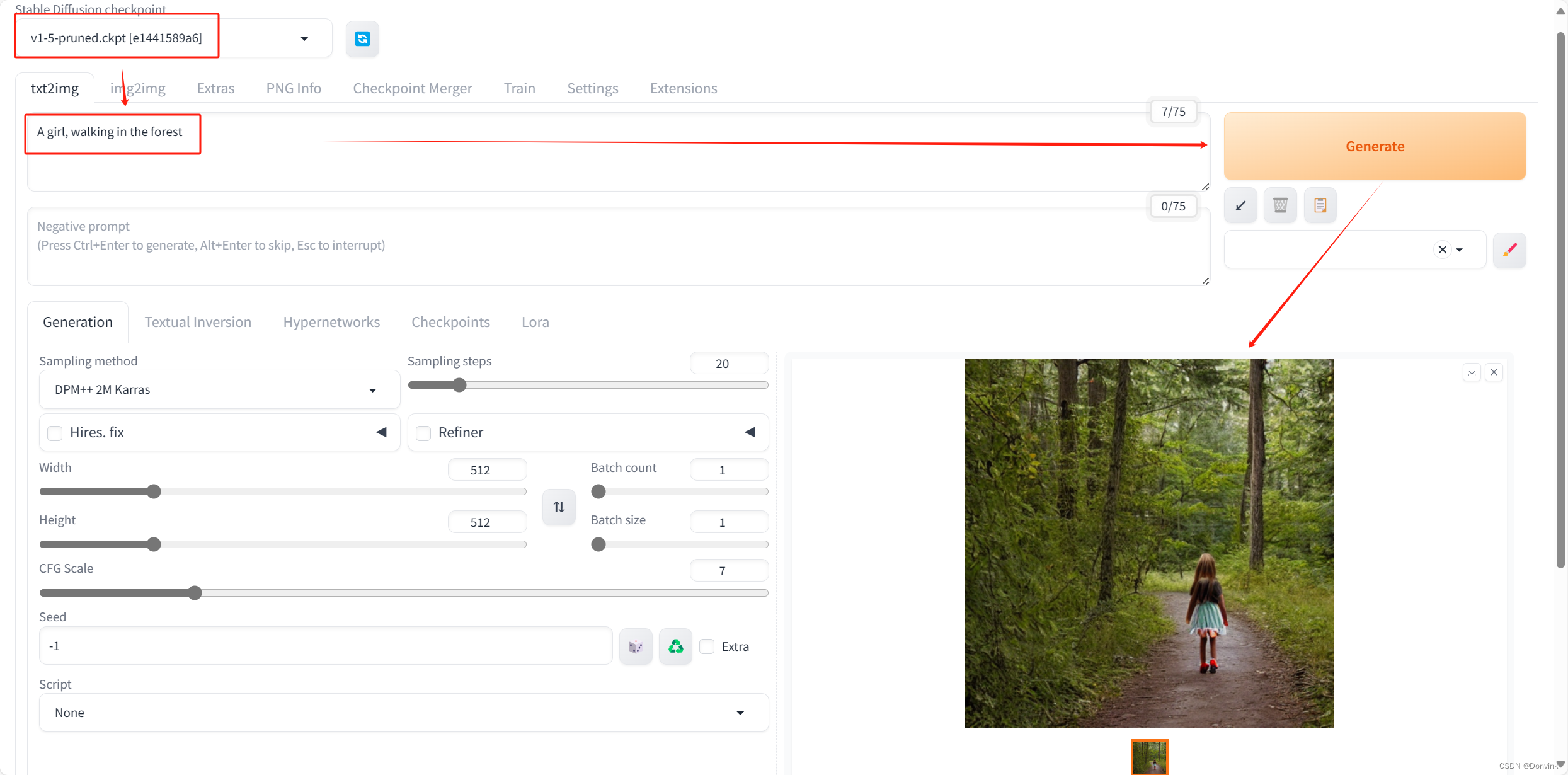
【Stable Diffusion】入门-01:原理简介+应用安装(Windows)+生成步骤
【Stable Diffusion】入门:原理简介应用安装(Windows)生成步骤 原理简介应用安装 原理简介 稳定扩散生成模型(Stable Diffusion)是一种潜在的文本到图像扩散模型,能够在给定任何文本输入的情况下生成照片般逼真的图像。 应用安…...

VueX详解
Vuex 主要应用于Vue.js中管理数据状态的一个库通过创建一个集中的数据存储,供程序中所有组件访问 使用场景 涉及到非父子关系的组件,例如兄弟关系、祖孙关系,甚至更远的关系组件之间的联系中大型单页应用,考虑如何更好地在组件外部…...

2023 年 9 月青少年软编等考 C 语言一级真题解析
目录 T1. 日期输出思路分析 T2. 计算 (a b) (c - b) 的值思路分析 T3. 有一门课不及格的学生思路分析 T4. 特殊求和T5. 比 n 小的最大质数 T1. 日期输出 给定两个整数,表示一个日期的月和日。请按照 "MM-DD" 的格式输出日期,即如果月和日不…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
