cmath 中cos sin等常用函数的坑(弧度角度换算)
cmath中三角函数的输入是弧度,不是角度.忘了这件事,找bug找了好久!
弧度是旧称弪。在数学和物理中,弧度是角的度量单位。它是由国际单位制导出的单位,单位缩写是rad。弧度是指在一个圆中,弧长和半径之比,即|弧度|=弧长÷半径。
角度是一个数学概念。用于描述角的大小,即两条相交直线中的任何一条与另一条相叠合时必须转动的量。度是用以度量角的大小的单位,符号为°。
弧度角度换算公式及函数:
弧度角度互换的函数:
#include<cmath>
#include<iostream>using namespace std;double Angle2Rad(double angle){//return angle*3.14159/180;return angle*0.017453293;
}double Rad2Angle(double Rad){//return Rad*180/3.14159;return Rad*57.29578;
}int main(){vector<double> angles = {45,60,150,180,250,270,360,720,-45,-90,-360,0};vector<double> rads = {0.785397,1.0472,2.61799,3.14159,4.36332,4.71238,6.28318,-0.785397,-1.57079,-6.28318,0};cout<<"以下是角度转弧度:"<<endl;for(auto angle:angles){cout<<angle<<"->"<<Angle2Rad(angle)<<endl;}cout<<"以下是弧度转角度"<<endl;for(auto rad:rads){cout<<rad<<"->"<<Rad2Angle(rad)<<endl;}return 0;
}结果:

各种三角函数
C++ 算法基础(1)——cmath常用函数_cmath 中关于除法的函数-CSDN博客
诱导公式
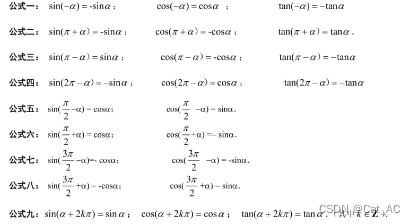
相关文章:
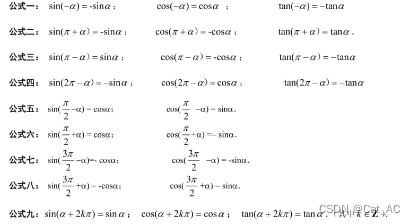
cmath 中cos sin等常用函数的坑(弧度角度换算)
cmath中三角函数的输入是弧度,不是角度.忘了这件事,找bug找了好久! 弧度是旧称弪。在数学和物理中,弧度是角的度量单位。它是由国际单位制导出的单位,单位缩写是rad。弧度是指在一个圆中,弧长和半径之比,即|弧度|弧长半径。 角度…...

深度解析HTTP反向代理-okey proxy
反向代理這個概念可能並不常見,但其實它對於提升網路安全和訪問速度方面發揮著很大作用。 HTTP反向代理(HTTP Reverse Proxy)是一種特殊的代理伺服器,首先它能夠接收互聯網上的連接請求,然後將這些請求轉發給內部網路…...

SwinIR训练报错解决
swinir训练报错解决 记录swinir图像超分重建算法复现过程中的报错信息,并提供相应的解决方案 报错信息 UserWarning: torch.meshgrid: in an upcoming release, it will be required to pass the indexing argument. (Triggered internally at C:\actions-runner\_work\pyto…...

C++类和对象一
#include <iostream> using namespace std;//设计一个学生类 class CStudent {public: //公有成员void InputData(){cout << "请输入学号";cin >> sno;cout << "请输入姓名";cin >> sname;cout << "请输入分…...

Linux之线程互斥
目录 一、问题引入 二、线程互斥 1、相关概念 2、加锁保护 1、静态分配 2、动态分配 3、锁的原理 4、死锁 三、可重入与线程安全 1、概念 2、常见的线程不安全的情况 3、常见的线程安全的情况 4、常见不可重入的情况 5、常见可重入的情况 6、可重入与线程安全联系…...
C++ 拷贝构造函数和运算符重载
目录 一. 拷贝构造函数 1. 引入 2. 拷贝构造的概念 3. 浅拷贝 4. 深拷贝 二. C运算符重载 1. 概念 2. 注意事项 3.举例 一. 拷贝构造函数 1. 引入 我们在创建对象时,能不能创建一个与原先对象一模一样的新对象呢?为了解决这个问题&#x…...

二刷代码随想录算法训练营第二十三天 | 669. 修剪二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树
目录 一、669. 修剪二叉搜索树 二、108. 将有序数组转换为二叉搜索树 三、538. 把二叉搜索树转换为累加树 一、669. 修剪二叉搜索树 题目链接:力扣 文章讲解:代码随想录 视频讲解: 你修剪的方式不对,我来给你纠正一下&#…...
信息抽取在旅游行业的应用:以景点信息抽取为例
开源项目推荐 今天先给大家推荐一个开源项目,多模态AI能力引擎平台: 免费的自然语言处理、情感分析、实体识别、图像识别与分类、OCR识别、语音识别接口,功能强大,欢迎体验。 https://gitee.com/stonedtx/free-nlp-api 场景描述 在旅游行业…...
Linux——基础指令
一、Linux目录结构 1、树形结构 Linux只有一个根目录 / ,所有文件都在它下面 2、Linux路径的描述方式 在Linux系统中,路径之间的层级关系,使用: / 来表示 eg: /usr/local/hello.txt 注意: 开头/表示根…...
H5 带网站测速引导页源码
源码名称:带网站测速引导页源码 源码介绍:一款带网站测速功能的引导页源码 需求环境:H5 下载地址: https://www.changyouzuhao.cn/10717.html...
案例分析篇07:数据库设计相关28个考点(23~28)(2024年软考高级系统架构设计师冲刺知识点总结系列文章)
专栏系列文章推荐: 2024高级系统架构设计师备考资料(高频考点&真题&经验)https://blog.csdn.net/seeker1994/category_12593400.html 【历年案例分析真题考点汇总】与【专栏文章案例分析高频考点目录】(2024年软考高级系统架构设计师冲刺知识点总结-案例分析篇-…...

Word中解决插入脚注导致的分页位置错误问题
先放一个截图: 上面的截图中,样式为标题3的段落“四、固执的念头”前插入了连续型分节符,并且该分节符的样式为正文,前后的正文段落中有脚注,结果在分页时,标题3段落“四、固执的念头”后的正文段落自动进入…...
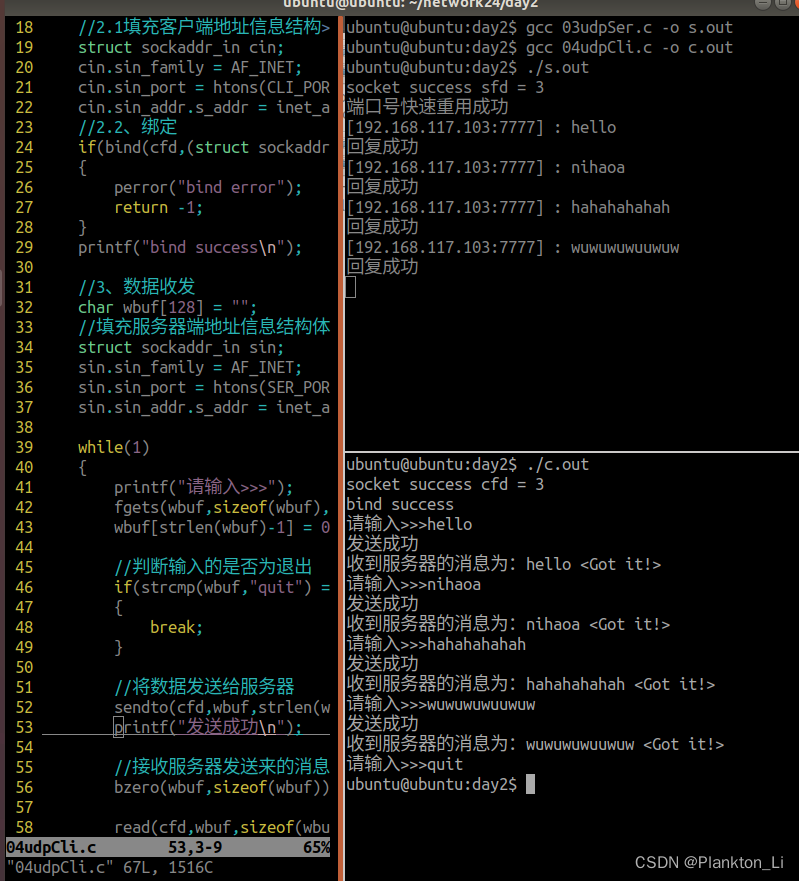
2024/03/14(网络编程·day2)
一、思维导图 二、TCP通信 //服务器 #include<myhead.h>#define SER_PORT 8888 //服务器端口号 #define SER_IP "192.168.117.103" //服务器IP int main(int argc, const char *argv[]) {//1、创建一个套接字int sfd -1;sfd socket(AF_INET,SOCK_STREAM,…...

2024最新陪诊小程序/医院陪诊滴嗒陪诊小程序源码-陪护服务平台陪诊师陪
.系统介绍: 陪护小程序、微信陪诊、、ThinkPHP框架、ThinkPHP6框架、FastAdmin框架、微信小程序。 嘀嗒陪诊小程序功能相对简单,后台也简捷,如果只是做个陪诊服务的小程序也基本能满足了,整体测试了未发现BUG,小程序端也能正常为使用,用户授权接口是老的。 应用背景:人…...

基于单片机的温度控制系统设计
基于单片机的温度控制系统设计 摘要: 最近这些年,随着科学技术的不断发展和进步,单片机技术通过在各行各业中的应用也日臻完善。而温度测控系统也因单片机所特有的强大处理能力、功耗低以及体积小等优点向着小型化和智能化发展。本设计以STC89C52单片机…...
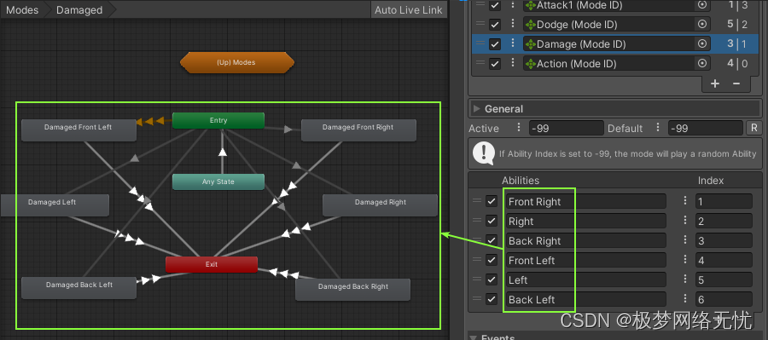
unity3d Animal Controller的Animal组件中Speeds,States和modes基础部分理解
Speeds 速度集是修改你可以做的原始动画,增加或减少运动,旋转,或动画速度。它们与 州 所以,当动物在运动状态下,在飞行或游泳时,你可以有不同的速度 如果你的性格动画是 (已到位), 你一定要调整速度 位置 和 旋转 每一种的价值观 速度装置 …否则,它们不会移动或旋转。 每个速…...

Tomcat详解
1Tomcat安装 下载 Tomcat:首先,您需要从 Tomcat 官方网站(http://tomcat.apache.org)下载适合您系统的最新版本的 Tomcat 软件包。通常情况下,您会选择一个稳定的版本进行下载。解压缩:下载完成后…...
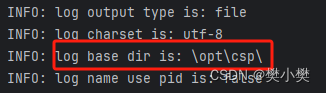
SpringCloudAlibaba 网关gateway整合sentinel日志默认路径修改
SpringCloudAlibaba 网关gateway整合sentinel 实现网关限流熔断 问题提出 今天运维突然告诉我 在服务器上内存满了 原因是nacos日志高达3G,然后将日志文件发给我看了一下之后才发现是gateway整合sentinel使用了默认日志地址导致日志生成地址直接存在与根路径下而且一下存在多…...

#LLM入门|Prompt#3.3_存储_Memory
在与语言模型交互时,一个关键问题:记忆缺失使得对话缺乏真正的连续性。 因此,接下来介绍 LangChain 中的储存模块,即如何将先前的对话嵌入到语言模型中的,使其具有连续对话的能力。 当使用 LangChain 中的储存(Memory)…...
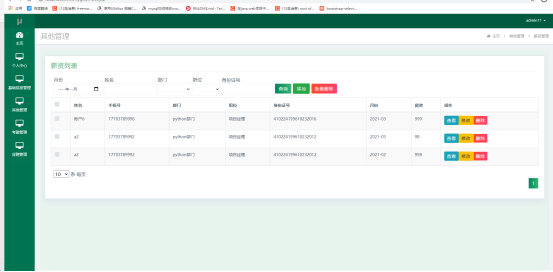
基于SSM+Vue的龙腾公司员工信息管理系统设计与实现
1 绪论 1.1研究背景 当前社会各行业领域竞争压力非常大,随着当前时代的信息化,科学化发展,让社会各行业领域都争相使用新的信息技术,对行业内的各种相关数据进行科学化,规范化管理。这样的大环境让那些止步不前&a…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
