二刷代码随想录算法训练营第二十三天 | 669. 修剪二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树
目录
一、669. 修剪二叉搜索树
二、108. 将有序数组转换为二叉搜索树
三、538. 把二叉搜索树转换为累加树
一、669. 修剪二叉搜索树
题目链接:力扣
文章讲解:代码随想录
视频讲解: 你修剪的方式不对,我来给你纠正一下!| LeetCode:669. 修剪二叉搜索树
题目:
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
代码:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:/*TreeNode* trimBST(TreeNode* root, int low, int high) {//没有很好的利用搜索树左小右大的特性if (!root) return root;root->left = trimBST(root->left, low, high);root->right = trimBST(root->right, low, high);if (root->val < low || root->val > high){if (!root->left) return root->right;else if (!root->right) return root->left;else{TreeNode* new_node = root->left;while(new_node->right) new_node = new_node->right;new_node->right = root->right;root = root->left;}}return root;//递归法if(!root) return NULL;if(root->val < low) return trimBST(root->right, low, high);if(root->val > high) return trimBST(root->left, low, high);root->left = trimBST(root->left, low, high);root->right = trimBST(root->right, low, high);return root;}*///递归法TreeNode* trimBST(TreeNode* root, int low, int high) {if (!root) return nullptr;//将根节点移到合理范围内while (root && (root->val < low || root->val > high))if (root->val < low) root = root->right;else root = root->left;TreeNode *node = root;// 处理左子树,处理左子树的过程中,合理继续向左(node的右子树一定合理),不合理就向右(node的左子树一定不合理)if(!root) return NULL;for (;node->left;) if(node->left->val < low) node->left = node->left->right;else node = node->left;// 处理右子树,处理右子树的过程中,合理继续向右(node的左子树一定合理),不合理就向左(node的右子树一定不合理)for (node = root;node->right;)if (node->right->val > high)node->right = node->right->left;else node = node->right;return root;}
};时间复杂度: O(n) 空间复杂度: O(1)
⏲:9:13
总结:1.考虑二叉搜索树特性,如果root结点不符合条件,那么左右子树有一个必不符合条件,另一个可能存在不符合条件的结点。
2.不考虑特性,则要删除root结点,则需要参考二叉树删除结点的方法。
二、108. 将有序数组转换为二叉搜索树
题目链接:力扣
文章讲解:代码随想录
视频讲解:构造平衡二叉搜索树!| LeetCode:108.将有序数组转换为二叉搜索树
题目:给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。 高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
代码:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* bulid(vector<int>& nums, int begin, int end){if(begin > end) return NULL;int mid = ((end - begin)>>1) + begin;TreeNode* root = new TreeNode(nums[mid]);root->left = bulid(nums, begin, mid-1);root->right = bulid(nums, mid+1, end);return root;}TreeNode* sortedArrayToBST(vector<int>& nums) {return bulid(nums, 0, nums.size()-1);}
};时间复杂度: O(n) 空间复杂度: O(logn)
⏲:4:11
总结:1.根据数组构造二叉树,考虑分治来递归。二叉搜索树要求顺序,则左子树在root左边,右子树在root右边。平衡二叉树要求左右结点数相近,则root结点选取mid。
三、538. 把二叉搜索树转换为累加树
题目链接:力扣
文章讲解:代码随想录
视频讲解:普大喜奔!二叉树章节已全部更完啦!| LeetCode:538.把二叉搜索树转换为累加树
题目:给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。 提醒一下,二叉搜索树满足下列约束条件: 节点的左子树仅包含键 小于 节点键的节点。 节点的右子树仅包含键 大于 节点键的节点。 左右子树也必须是二叉搜索树。
代码:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* pre;TreeNode* convertBST(TreeNode* root) {if (!root) return NULL;convertBST(root->right);if (pre) root->val += pre->val;pre = root;convertBST(root->left);return root;}
};时间复杂度: O(n) 空间复杂度O(n)
⏲:2:21
总结:1、观察知,所谓累计所有比自己大的结点的值在二叉搜索树(中序遍历可变为有序数组)中,可表现为自身的值加上上一个结点的值(已经累加过)即可。故采用反中序遍历即从大到小进行累加。
2、迭代法可通过构造线索二叉树,将空间复杂度压缩为O(1)。
相关文章:

二刷代码随想录算法训练营第二十三天 | 669. 修剪二叉搜索树、108.将有序数组转换为二叉搜索树、538.把二叉搜索树转换为累加树
目录 一、669. 修剪二叉搜索树 二、108. 将有序数组转换为二叉搜索树 三、538. 把二叉搜索树转换为累加树 一、669. 修剪二叉搜索树 题目链接:力扣 文章讲解:代码随想录 视频讲解: 你修剪的方式不对,我来给你纠正一下&#…...
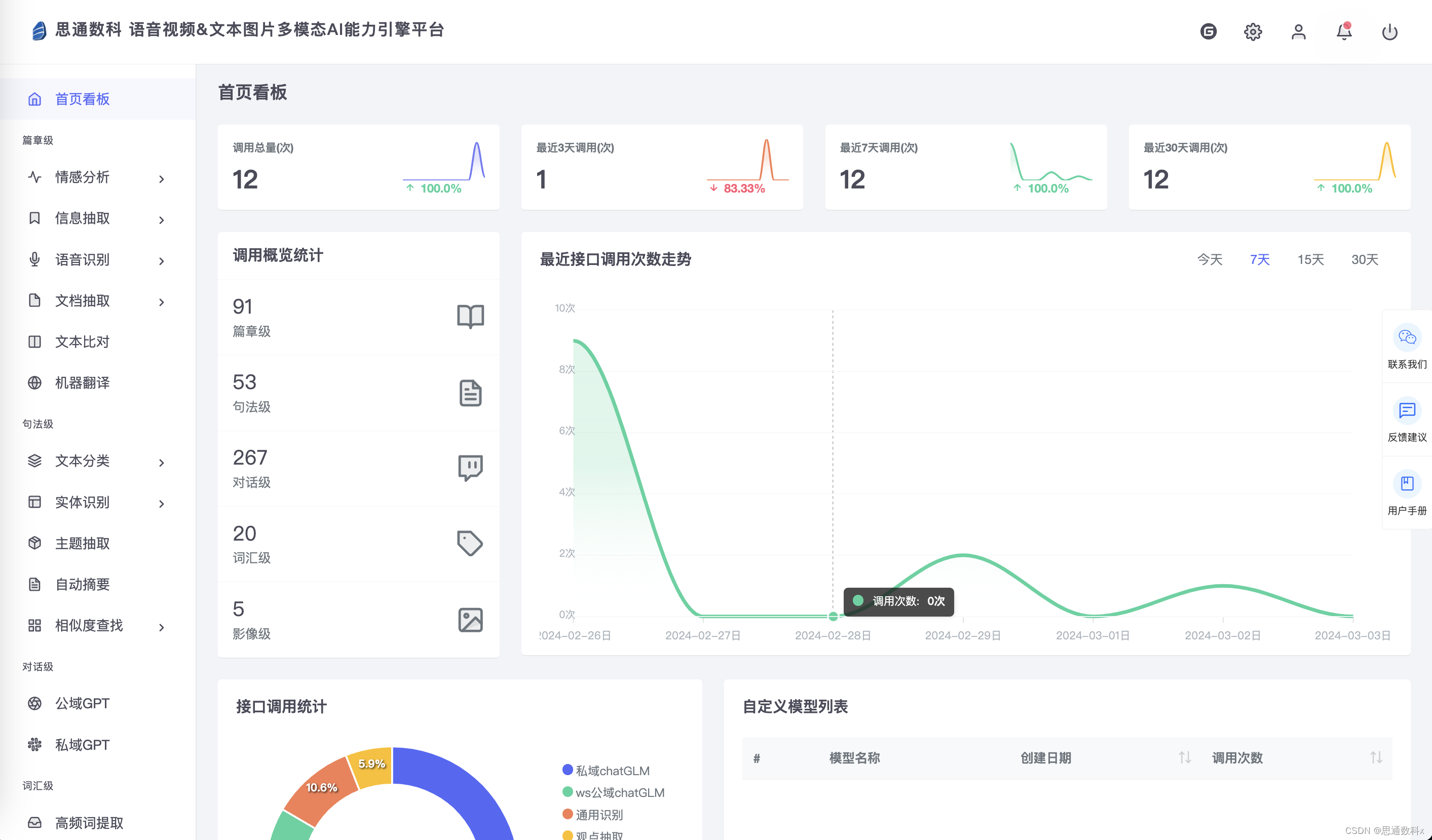
信息抽取在旅游行业的应用:以景点信息抽取为例
开源项目推荐 今天先给大家推荐一个开源项目,多模态AI能力引擎平台: 免费的自然语言处理、情感分析、实体识别、图像识别与分类、OCR识别、语音识别接口,功能强大,欢迎体验。 https://gitee.com/stonedtx/free-nlp-api 场景描述 在旅游行业…...
Linux——基础指令
一、Linux目录结构 1、树形结构 Linux只有一个根目录 / ,所有文件都在它下面 2、Linux路径的描述方式 在Linux系统中,路径之间的层级关系,使用: / 来表示 eg: /usr/local/hello.txt 注意: 开头/表示根…...
H5 带网站测速引导页源码
源码名称:带网站测速引导页源码 源码介绍:一款带网站测速功能的引导页源码 需求环境:H5 下载地址: https://www.changyouzuhao.cn/10717.html...
案例分析篇07:数据库设计相关28个考点(23~28)(2024年软考高级系统架构设计师冲刺知识点总结系列文章)
专栏系列文章推荐: 2024高级系统架构设计师备考资料(高频考点&真题&经验)https://blog.csdn.net/seeker1994/category_12593400.html 【历年案例分析真题考点汇总】与【专栏文章案例分析高频考点目录】(2024年软考高级系统架构设计师冲刺知识点总结-案例分析篇-…...

Word中解决插入脚注导致的分页位置错误问题
先放一个截图: 上面的截图中,样式为标题3的段落“四、固执的念头”前插入了连续型分节符,并且该分节符的样式为正文,前后的正文段落中有脚注,结果在分页时,标题3段落“四、固执的念头”后的正文段落自动进入…...
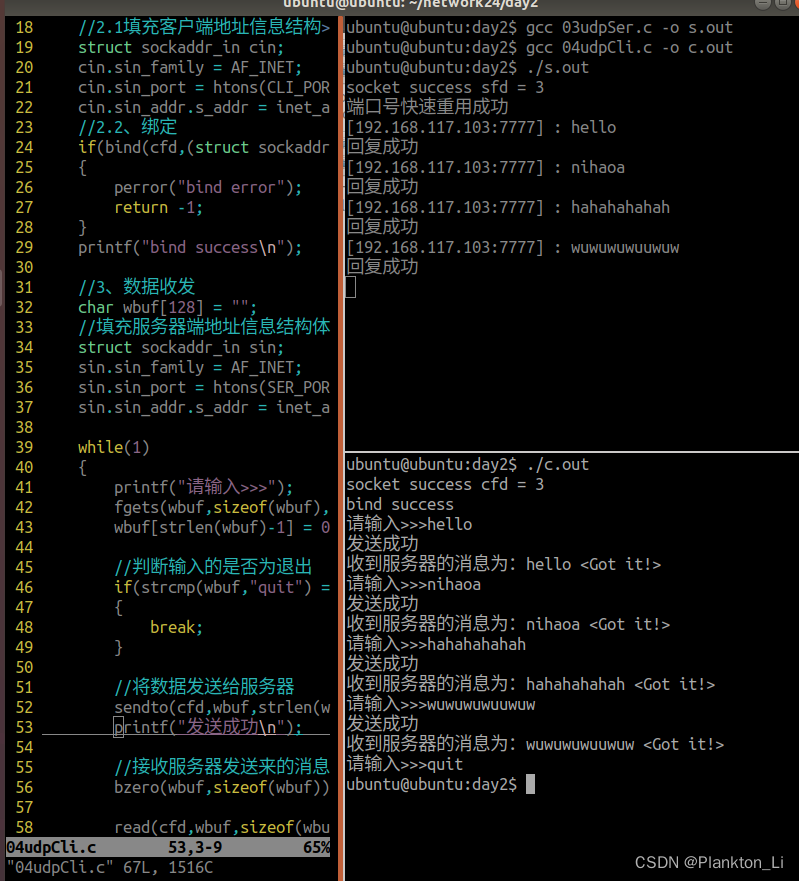
2024/03/14(网络编程·day2)
一、思维导图 二、TCP通信 //服务器 #include<myhead.h>#define SER_PORT 8888 //服务器端口号 #define SER_IP "192.168.117.103" //服务器IP int main(int argc, const char *argv[]) {//1、创建一个套接字int sfd -1;sfd socket(AF_INET,SOCK_STREAM,…...

2024最新陪诊小程序/医院陪诊滴嗒陪诊小程序源码-陪护服务平台陪诊师陪
.系统介绍: 陪护小程序、微信陪诊、、ThinkPHP框架、ThinkPHP6框架、FastAdmin框架、微信小程序。 嘀嗒陪诊小程序功能相对简单,后台也简捷,如果只是做个陪诊服务的小程序也基本能满足了,整体测试了未发现BUG,小程序端也能正常为使用,用户授权接口是老的。 应用背景:人…...

基于单片机的温度控制系统设计
基于单片机的温度控制系统设计 摘要: 最近这些年,随着科学技术的不断发展和进步,单片机技术通过在各行各业中的应用也日臻完善。而温度测控系统也因单片机所特有的强大处理能力、功耗低以及体积小等优点向着小型化和智能化发展。本设计以STC89C52单片机…...
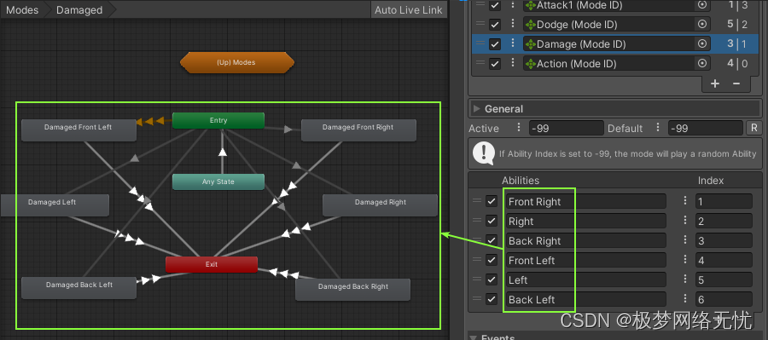
unity3d Animal Controller的Animal组件中Speeds,States和modes基础部分理解
Speeds 速度集是修改你可以做的原始动画,增加或减少运动,旋转,或动画速度。它们与 州 所以,当动物在运动状态下,在飞行或游泳时,你可以有不同的速度 如果你的性格动画是 (已到位), 你一定要调整速度 位置 和 旋转 每一种的价值观 速度装置 …否则,它们不会移动或旋转。 每个速…...

Tomcat详解
1Tomcat安装 下载 Tomcat:首先,您需要从 Tomcat 官方网站(http://tomcat.apache.org)下载适合您系统的最新版本的 Tomcat 软件包。通常情况下,您会选择一个稳定的版本进行下载。解压缩:下载完成后…...
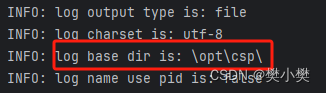
SpringCloudAlibaba 网关gateway整合sentinel日志默认路径修改
SpringCloudAlibaba 网关gateway整合sentinel 实现网关限流熔断 问题提出 今天运维突然告诉我 在服务器上内存满了 原因是nacos日志高达3G,然后将日志文件发给我看了一下之后才发现是gateway整合sentinel使用了默认日志地址导致日志生成地址直接存在与根路径下而且一下存在多…...

#LLM入门|Prompt#3.3_存储_Memory
在与语言模型交互时,一个关键问题:记忆缺失使得对话缺乏真正的连续性。 因此,接下来介绍 LangChain 中的储存模块,即如何将先前的对话嵌入到语言模型中的,使其具有连续对话的能力。 当使用 LangChain 中的储存(Memory)…...
基于SSM+Vue的龙腾公司员工信息管理系统设计与实现
1 绪论 1.1研究背景 当前社会各行业领域竞争压力非常大,随着当前时代的信息化,科学化发展,让社会各行业领域都争相使用新的信息技术,对行业内的各种相关数据进行科学化,规范化管理。这样的大环境让那些止步不前&a…...
使用点链云管家创建瑜伽约课小程序
点链云管家 点链云管家是由上海点链科技开发的门店管理系统,为线下门店商家提供一站式门店运营服务平台解决方案,适用于瑜伽健身、美业、新零售会员制电商、母婴店、宠物店、按摩养生、服装、美容、美甲、汽车服务、商超零售、餐饮、KTV娱乐、干洗等18个…...

【Node.js从基础到高级运用】八、Express 框架入门
Express 框架入门 Express 是一个灵活且广泛使用的 Node.js web 应用框架,它提供了一系列强大特性来帮助开发者创建各种 Web 和移动设备应用。在这一节中,我们将介绍如何安装和配置 Express,并简单探讨其路由和中间件的概念。 安装 Express…...
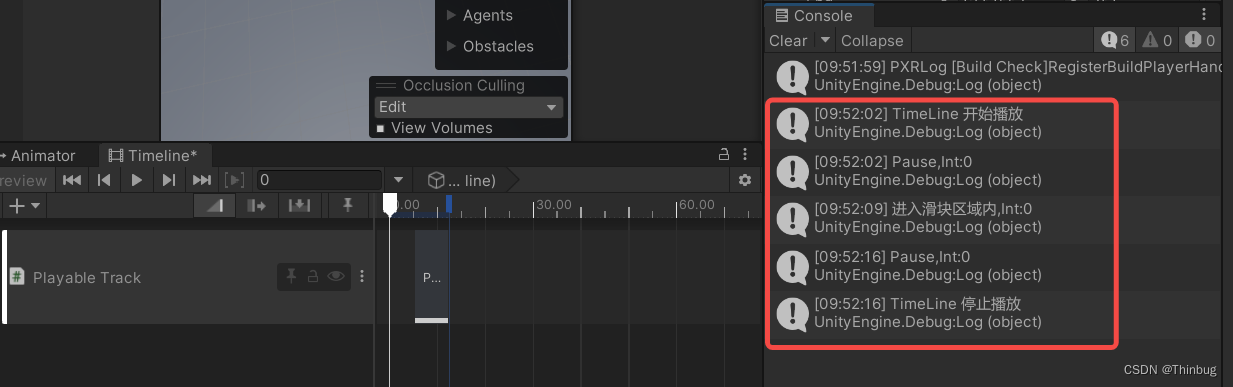
Unity Timeline学习笔记(2) - PlayableTrack
PlayableTrack 是可自定义播放的轨道。我们可以通过进入轨道后调用自己的函数方法,使用起来也是比较顺手的。 添加轨道 我们点击加号添加 这样就有一个空轨道了,然后我们创建两个测试脚本。 添加脚本 分别是Playable Behaviour和PlayableAsset脚本。…...
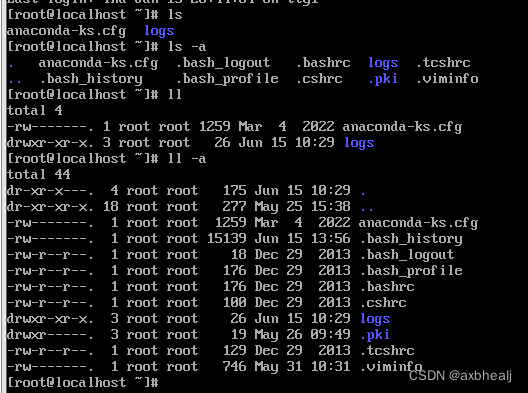
Linux的一些常用指令
一、文件中 r w x - 的含义 r(read)是只读权限, w(write)是写的权限, x(execute)是可执行权限, -是没有任何权限。 二、一些指令 # 解压压缩包 tar [-zxvf] 压缩包名…...

09-设计模式 企业场景 面试题
目录 1.简单工厂模式 编辑 2.工厂方法模式 3.抽象工厂模式 4.策略模式 5.登录案例(工厂模式+策略模式) 6.责任链设计模式 7.单点登录怎么是实现的? 8.权限认证是如何实现的 9.上传数据的安全性你们怎么控制? 10.你负责项目的时候遇到了哪些比较棘手的问题?怎…...
计算机组成原理-练手题集合【期末复习|考研复习】
前言 总结整理不易,希望大家点赞收藏。 给大家整理了一下计算机组成原理中的各章练手题,以供大家期末复习和考研复习的时候使用。 参考资料是王道的计算机组成原理和西电的计算机组成原理。 计算机组成原理系列文章传送门: 第一/二章 概述和数…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
