代码随想录 贪心算法-中等题目-序列问题
目录
376.摆动序列
738.单调递增的数字
376.摆动序列
376. 摆动序列
中等
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
-
例如,
[1, 7, 4, 9, 2, 5]是一个 摆动序列 ,因为差值(6, -3, 5, -7, 3)是正负交替出现的。 - 相反,
[1, 4, 7, 2, 5]和[1, 7, 4, 5, 5]不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
示例 1:
输入:nums = [1,7,4,9,2,5] 输出:6 解释:整个序列均为摆动序列,各元素之间的差值为 (6, -3, 5, -7, 3) 。
示例 2:
输入:nums = [1,17,5,10,13,15,10,5,16,8] 输出:7 解释:这个序列包含几个长度为 7 摆动序列。 其中一个是 [1, 17, 10, 13, 10, 16, 8] ,各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。
示例 3:
输入:nums = [1,2,3,4,5,6,7,8,9] 输出:2
提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000
进阶:你能否用 O(n) 时间复杂度完成此题?
class Solution { // 定义一个公共方法wiggleMaxLength,接收一个整数数组nums作为参数,返回摆动长度 public int wiggleMaxLength(int[] nums) { // 如果数组长度小于等于1,则摆动长度等于数组长度 if (nums.length <= 1) { return nums.length; } // 当前差值,初始化为0 // 表示当前元素与前一个元素的差值 int curDiff = 0; // 上一个差值,初始化为0 // 表示前一个元素与前一个元素的差值 // 在第一次循环时,preDiff实际上是一个“初始值”,用于比较 int preDiff = 0; // 摆动长度,初始化为1 // 因为至少有一个元素,所以摆动长度至少为1 int count = 1; // 从数组的第二个元素开始遍历 for (int i = 1; i < nums.length; i++) { // 计算当前差值 curDiff = nums[i] - nums[i - 1]; // 判断当前差值与上一个差值的符号是否相反 // 如果相反,说明摆动长度增加 // 注意:curDiff > 0 && preDiff <= 0 表示当前差值为正,且上一个差值为负或零 // curDiff < 0 && preDiff >= 0 表示当前差值为负,且上一个差值为正或零 if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) { count++; // 摆动长度增加 preDiff = curDiff; // 更新上一个差值为当前差值 } } // 返回摆动长度 return count; }
}要求删除元素使其达到最大摆动序列,应该删除什么元素呢?

局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。
整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。
实际操作上,其实连删除的操作都不用做,因为题目要求的是最长摆动子序列的长度,所以只需要统计数组的峰值数量就可以了
在计算是否有峰值的时候,大家知道遍历的下标 i ,计算 prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i]),如果prediff < 0 && curdiff > 0 或者 prediff > 0 && curdiff < 0 此时就有波动就需要统计。
这是我们思考本题的一个大题思路,但本题要考虑三种情况:
- 情况一:上下坡中有平坡
- 情况二:数组首尾两端
- 情况三:单调坡中有平坡
情况一:上下坡中有平坡
例如 [1,2,2,2,1]这样的数组,如图:
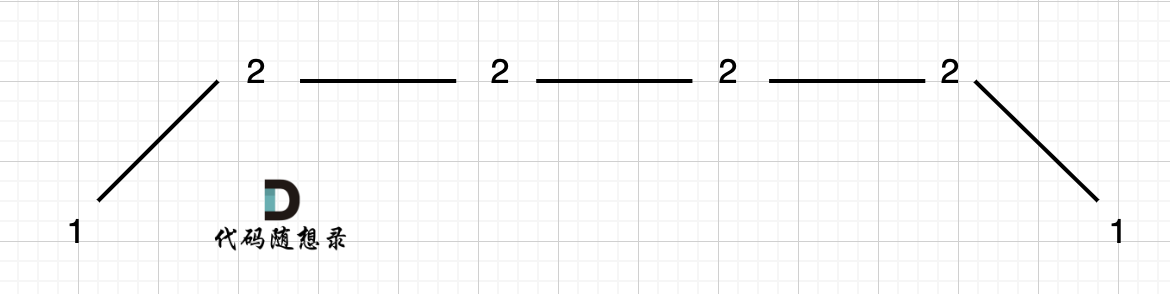
它的摇摆序列长度是多少呢? 其实是长度是 3,也就是我们在删除的时候 要不删除左面的三个 2,要不就删除右边的三个 2。
如图,可以统一规则,删除左边的三个 2:

在图中,当 i 指向第一个 2 的时候,prediff > 0 && curdiff = 0 ,当 i 指向最后一个 2 的时候 prediff = 0 && curdiff < 0。
如果我们采用,删左面三个 2 的规则,那么 当 prediff = 0 && curdiff < 0 也要记录一个峰值,因为他是把之前相同的元素都删掉留下的峰值。
所以我们记录峰值的条件应该是: (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0),为什么这里允许 prediff == 0 ,就是为了 上面我说的这种情况。
情况二:数组首尾两端
所以本题统计峰值的时候,数组最左面和最右面如何统计呢?
题目中说了,如果只有两个不同的元素,那摆动序列也是 2。
例如序列[2,5],如果靠统计差值来计算峰值个数就需要考虑数组最左面和最右面的特殊情况。
因为我们在计算 prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i])的时候,至少需要三个数字才能计算,而数组只有两个数字。
不写死的话,如何和我们的判断规则结合在一起呢?
可以假设,数组最前面还有一个数字,那这个数字应该是什么呢?
那么为了规则统一,针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即 preDiff = 0(即将preDif初始化为0),如图:
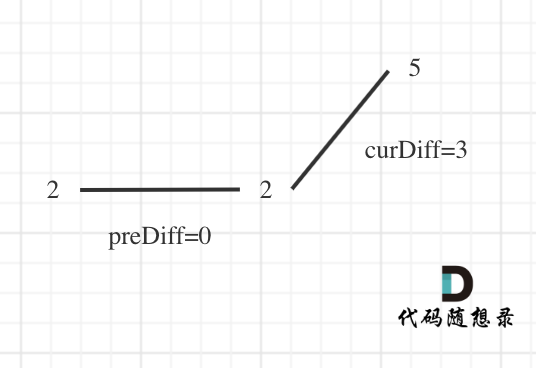
针对以上情形,result 初始为 1(默认最左面有一个峰值),此时 curDiff > 0 && preDiff <= 0,那么 result++(计算了左面的峰值),最后得到的 result 就是 2(峰值个数为 2 即摆动序列长度为 2)
情况三:单调坡度有平坡
在版本一中,我们忽略了一种情况,即 如果在一个单调坡度上有平坡,例如[1,2,2,2,3,4],如图:
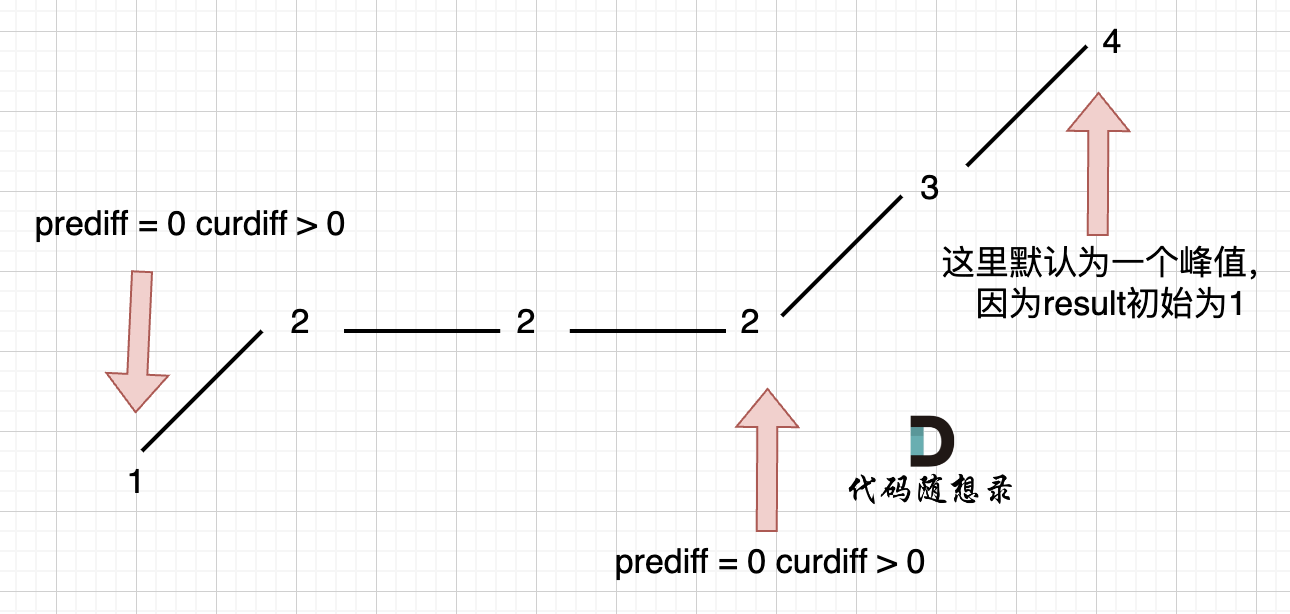
图中,我们可以看出,版本一的代码在三个地方记录峰值,但其实结果因为是 2,因为 单调中的平坡 不能算峰值(即摆动)。
之所以版本一会出问题,是因为我们实时更新了 prediff。
那么我们应该什么时候更新 prediff 呢?
我们只需要在 这个坡度 摆动变化的时候,更新 prediff 就行,这样 prediff 在 单调区间有平坡的时候 就不会发生变化,造成我们的误判。
738.单调递增的数字
738. 单调递增的数字
中等
提示
当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。
给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。
示例 1:
输入: n = 10 输出: 9
示例 2:
输入: n = 1234 输出: 1234
示例 3:
输入: n = 332 输出: 299
提示:
0 <= n <= 109
思路是在原来给出的数字中处理,从后向前遍历,如果遇到前一个数大于后一个数的情况,就将该前一个数减1,将后面的数字都改为9,这样既保持了递增,又使得最后的结果最大
class Solution { public int monotoneIncreasingDigits(int n) { // 将整数n转换为字符串 String s = String.valueOf(n); // 将字符串转换为字符数组,方便进行字符操作 char[] sChar = s.toCharArray(); // 初始化start为数组长度,表示还没有找到需要修改的位置 int start = sChar.length; // 从数组倒数第二个字符开始向前遍历 for(int i = sChar.length - 2; i >= 0; i--){ // 如果当前字符大于下一个字符,说明不满足单调递增的条件 if(sChar[i] > sChar[i + 1]){ // 更新start为当前位置+1,表示从当前位置开始后面的字符都需要变为9 start = i + 1; // 将当前字符减1,以便让后续字符满足单调递增的条件 sChar[i] -= 1; } } // 从start位置开始,将后面的所有字符都变为'9',以满足单调递增的条件 for(int i = start; i < sChar.length; i++){ sChar[i] = '9'; } // 将修改后的字符数组转换回整数 int num = Integer.parseInt(String.valueOf(sChar)); // 返回修改后的整数 return num; }
}题目要求小于等于N的最大单调递增的整数,那么拿一个两位的数字来举例。
例如:98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]--,然后strNum[i]给为9,这样这个整数就是89,即小于98的最大的单调递增整数。
这一点如果想清楚了,这道题就好办了。
此时是从前向后遍历还是从后向前遍历呢?
从前向后遍历的话,遇到strNum[i - 1] > strNum[i]的情况,让strNum[i - 1]减一,但此时如果strNum[i - 1]减一了,可能又小于strNum[i - 2]。
这么说有点抽象,举个例子,数字:332,从前向后遍历的话,那么就把变成了329,此时2又小于了第一位的3了,真正的结果应该是299。
那么从后向前遍历,就可以重复利用上次比较得出的结果了,从后向前遍历332的数值变化为:332 -> 329 -> 299
确定了遍历顺序之后,那么此时局部最优就可以推出全局,找不出反例,试试贪心。
相关文章:

代码随想录 贪心算法-中等题目-序列问题
目录 376.摆动序列 738.单调递增的数字 376.摆动序列 376. 摆动序列 中等 如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列…...
pytest生成allure的报告
首先要下载安装配置allure allure serve ./outputs/allure_report 可以生成html的文件自动在默认浏览器中打开...
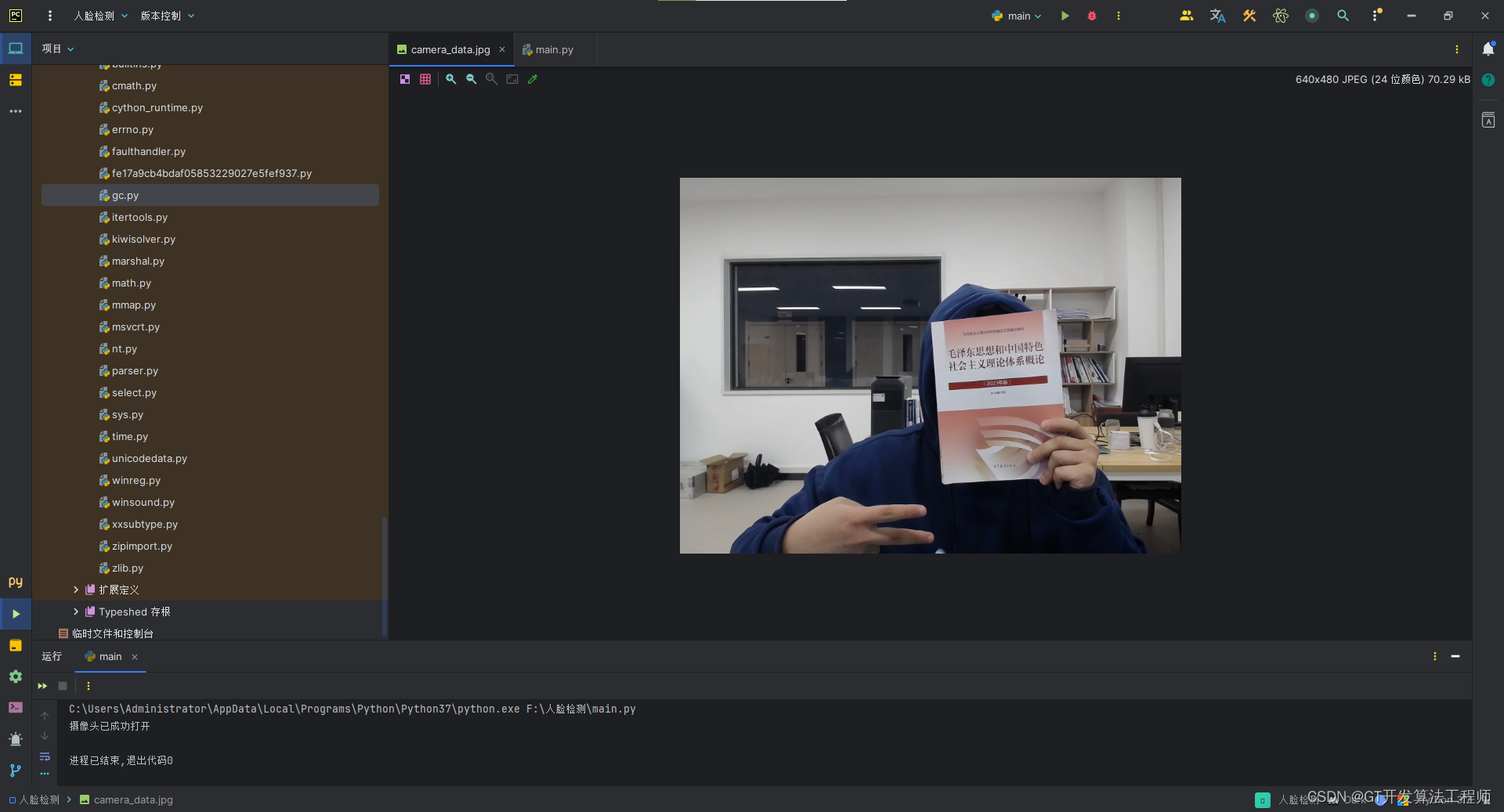
Python控制摄像头并获取数据文件
一、引言 摄像头作为计算机视觉领域的核心设备之一,广泛应用于视频监控、图像采集和数据处理等领域。通过Python编程语言,我们可以实现对摄像头的精确控制,包括摄像头的开启、关闭、参数设置以及数据获取等功能。 目录 一、引言 二、摄像头…...
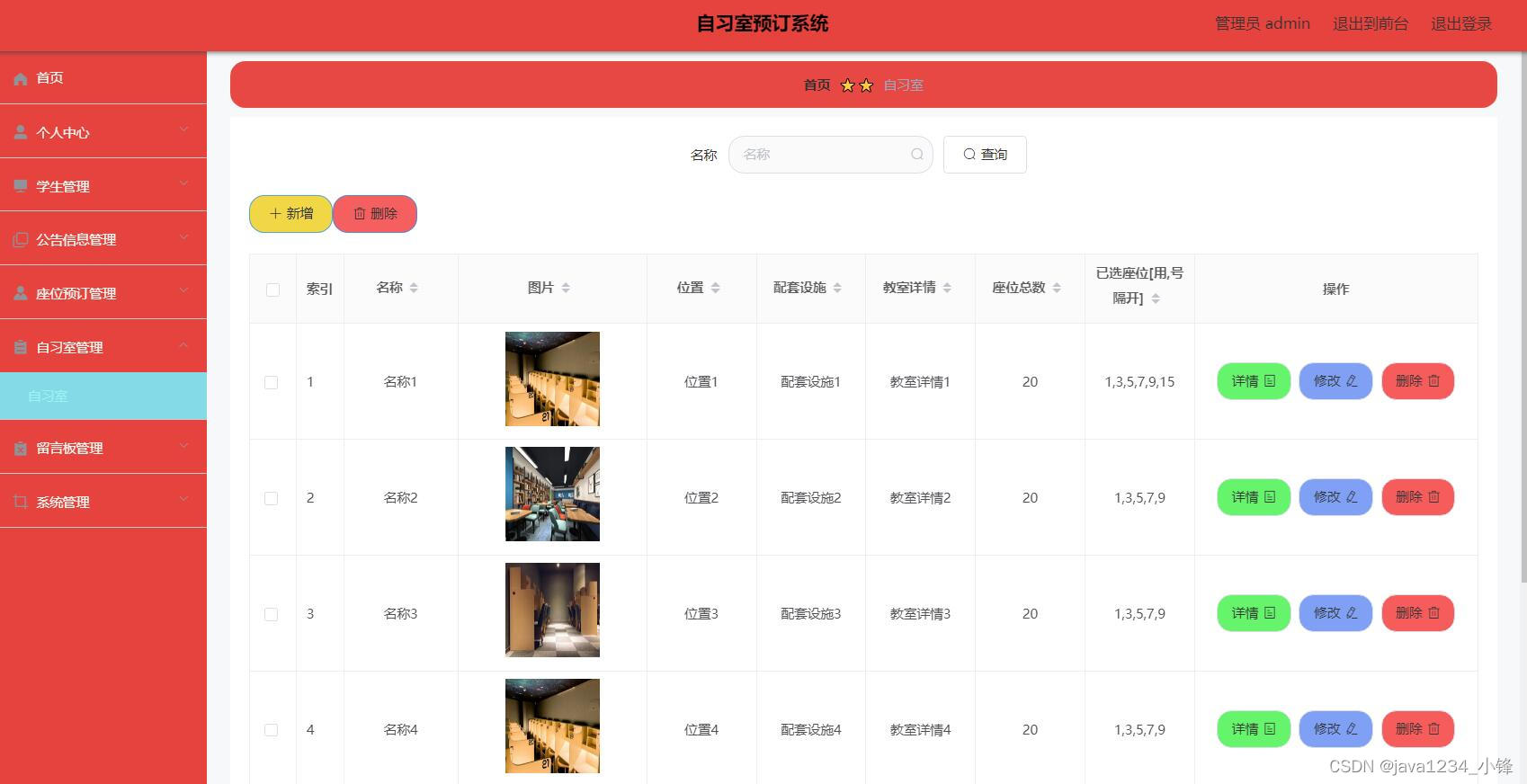
免费分享一套SpringBoot+Vue自习室(预约)管理系统,帅呆了~~
大家好,我是java1234_小锋老师,看到一个不错的SpringBootVue自习室预约)管理系统,分享下哈。 项目视频演示 【免费】SpringBootVue自习室预约(预约)管理系统 Java毕业设计_哔哩哔哩_bilibili【免费】SpringBootVue自习室预约(预约)管理系统…...

mac删除带锁标识的app
一 、我们这里要删除FortiClient.app 带锁 常规方式删除不掉带锁的 app【如下图】 二、删除命令,依次执行即可。 /bin/ls -dleO /Applications/FortiClient.app sudo /usr/bin/chflags -R noschg /Applications/FortiClient.app /bin/ls -dleO /Applications/Forti…...
PHP异世界云商系统开源源码
系统更新与修复列表 1. 基于彩虹的二次开发 - 对彩虹系统进行了二次开发,增强了系统的功能和性能。2. 新增自定义输入框提示内容(支持批量修改) - 用户可以自定义输入框的提示内容,并支持批量修改,提升用户体验。3. 新…...

Vue生成Canvas二维码
npm install qrcode在Vue组件中引入QRCode库:import QRCode from qrcode;在Vue组件的methods中创建一个方法来生成二维码: generateQRCode() {const canvas this.$refs.qrCodeCanvas; // 获取canvas DOM元素的引用const text Hello, World!; // 要生成…...
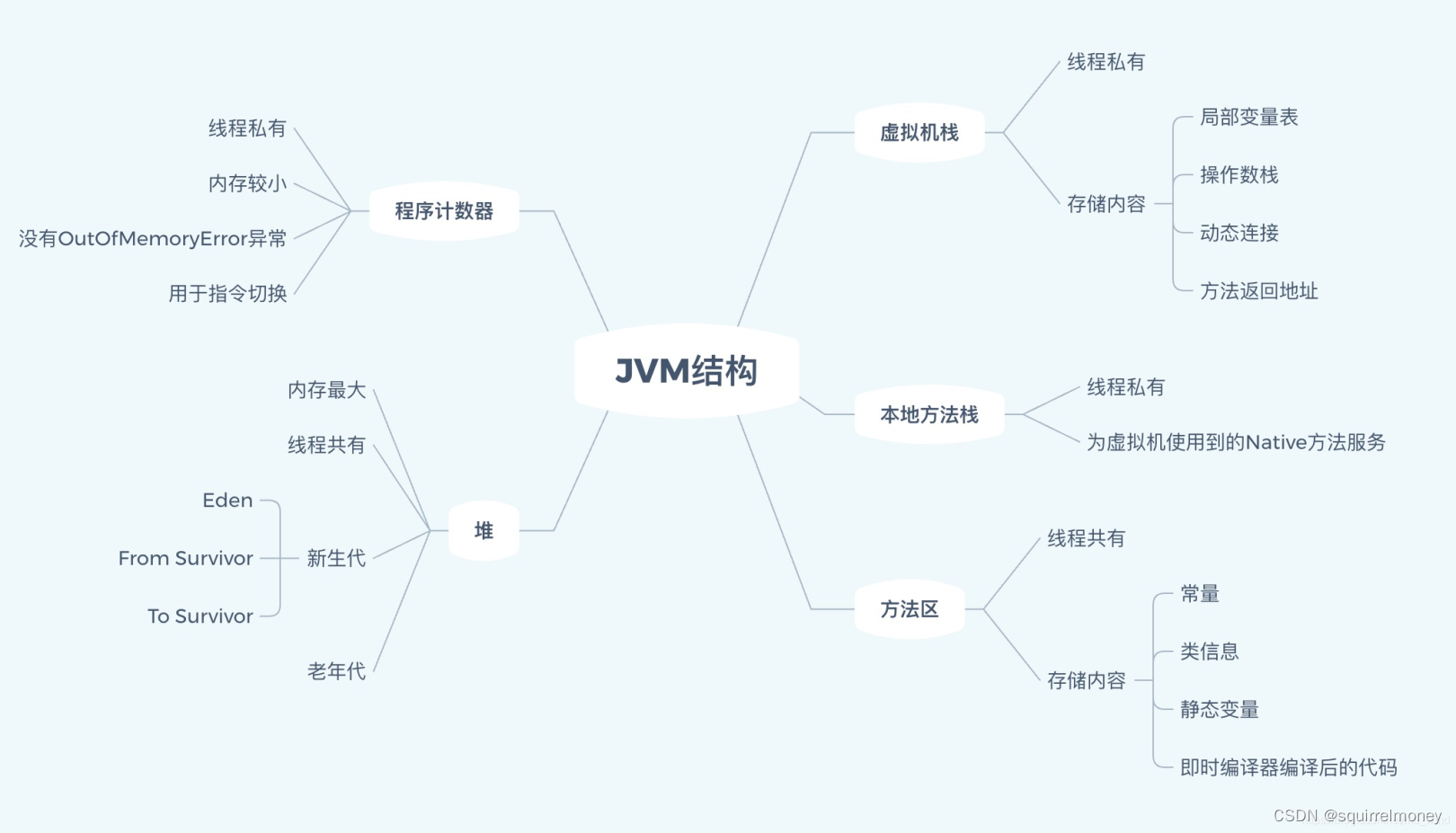
JAVA基础—JVM内存结构基础需知
1.JVM内存结构 JVM内存结构分为5个区域:方法区,虚拟机栈,本地方法栈、堆、程序计数器。 1.方法区(Method Area):用于存储类的结构信息、常量、静态变量、即使编译器编译后的代码等数据。方法区也是所有线…...

【滤波专题-第8篇】ICA降噪方法——类EMD联合ICA降噪及MATLAB代码实现(以VMD-ICA为例)
今天来介绍一种效果颇为不错的降噪方法。(针对高频白噪声) 上一篇文章我们讲到了FastICA方法。在现实世界的许多情况下,噪声往往接近高斯分布,而有用的信号(如语音、图像特征等)往往表现出非高斯的特性。F…...
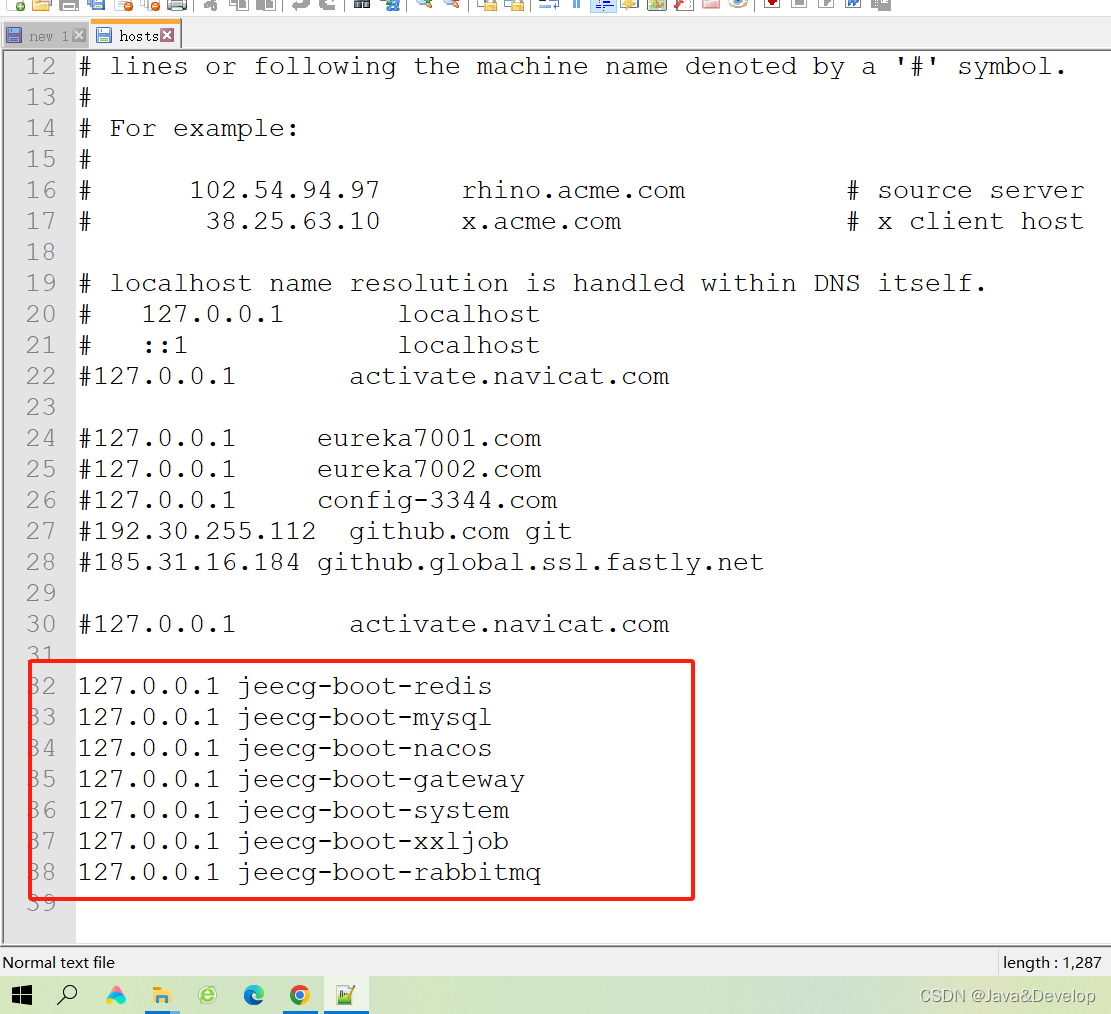
jeecg 启动 微服务 更改配置本地host地址
127.0.0.1 jeecg-boot-redis 127.0.0.1 jeecg-boot-mysql 127.0.0.1 jeecg-boot-nacos 127.0.0.1 jeecg-boot-gateway 127.0.0.1 jeecg-boot-system 127.0.0.1 jeecg-boot-sentinel 127.0.0.1 jeecg-boot-xxljob 127.0.0.1 jeecg-boot-rabbitmq1. windows系统下,在开…...
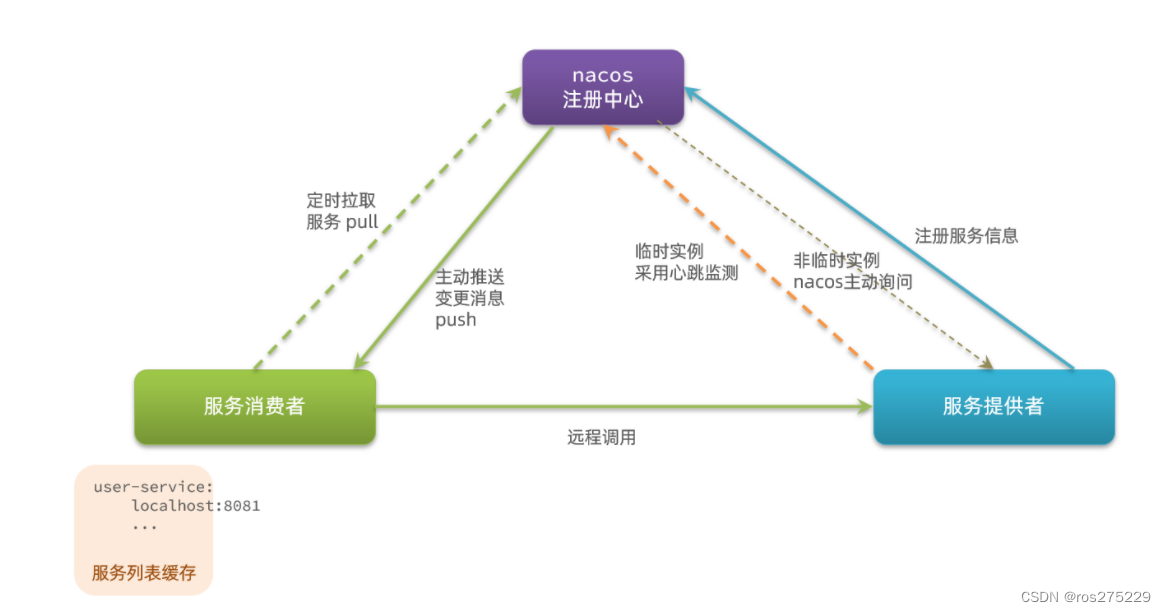
微服务day01 -- SpringCloud01 -- (Eureka , Ribbon , Nacos)
介绍微服务 1.认识微服务(p1-p5) 随着互联网行业的发展,对服务的要求也越来越高,服务架构也从单体架构逐渐演变为现在流行的微服务架构。这些架构之间有怎样的差别呢? 1.0.学习目标 了解微服务架构的优缺点 1.1.单体架构 单体架构&#…...
:2024.03.10-2024.03.15)
AI推介-大语言模型LLMs论文速览(arXiv方向):2024.03.10-2024.03.15
文章目录~ 1.Large Language Models and Causal Inference in Collaboration: A Comprehensive Survey2.VisionGPT-3D: A Generalized Multimodal Agent for Enhanced 3D Vision Understanding3.MT-PATCHER: Selective and Extendable Knowledge Distillation from Large Langu…...

ThingsBoard Edge 安装部署
文章目录 一、概述1.官方文档2.部署说明3.安装准备3.1. 克隆服务器3.2.安装 Docker3.3.安装 Java 113.4.安装 PostgreSQL3.5.下载安装包 二、安装部署1.创建 Edge 实例2.创建数据库3.Edge 服务安装3.1.安装服务3.2.配置 Edge3.3.运行安装脚本3.4.重新启动服务 4.访问 Edge5.故障…...

CSS进阶空间转换和 less
<html> <head> <meta charset"UTF-8" /> <title>空间转换</title> </head> <body> <!-- 空间转换 空间:是从坐标轴角度定义的X,Y,和Z三条坐标轴构成一个立体空间 Z轴位置与视线方向相同 空间转换也叫3D转…...

C/C++ 知识点:| 与 || 的区别
文章目录 一、|与 || 的区别1、按位或运算符 |2、逻辑或运算符 ||3、区别4、总结 前言 在C编程语言中,逻辑或运算符用于连接两个条件表达式,当至少有一个条件为真时,整个表达式的结果为真。C提供了两种逻辑或运算符:按位或|和逻辑…...
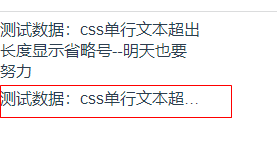
CSS中如何设置单行或多行内容超出后,显示省略号
1. 设置超出显示省略号 css设置超出显示省略号可分两种情况: 单行文本溢出显示省略号…多行文本溢出显示省略号… 但使用的核心代码是一样的:需要先使用 overflow:hidden;来把超出的部分隐藏,然后使用text-overflow:ellipsis;当文本超出时…...

PFA烧杯透明聚四氟乙烯刻度量杯
PFA烧杯,刻度清晰,耐酸碱,和有机溶剂。...
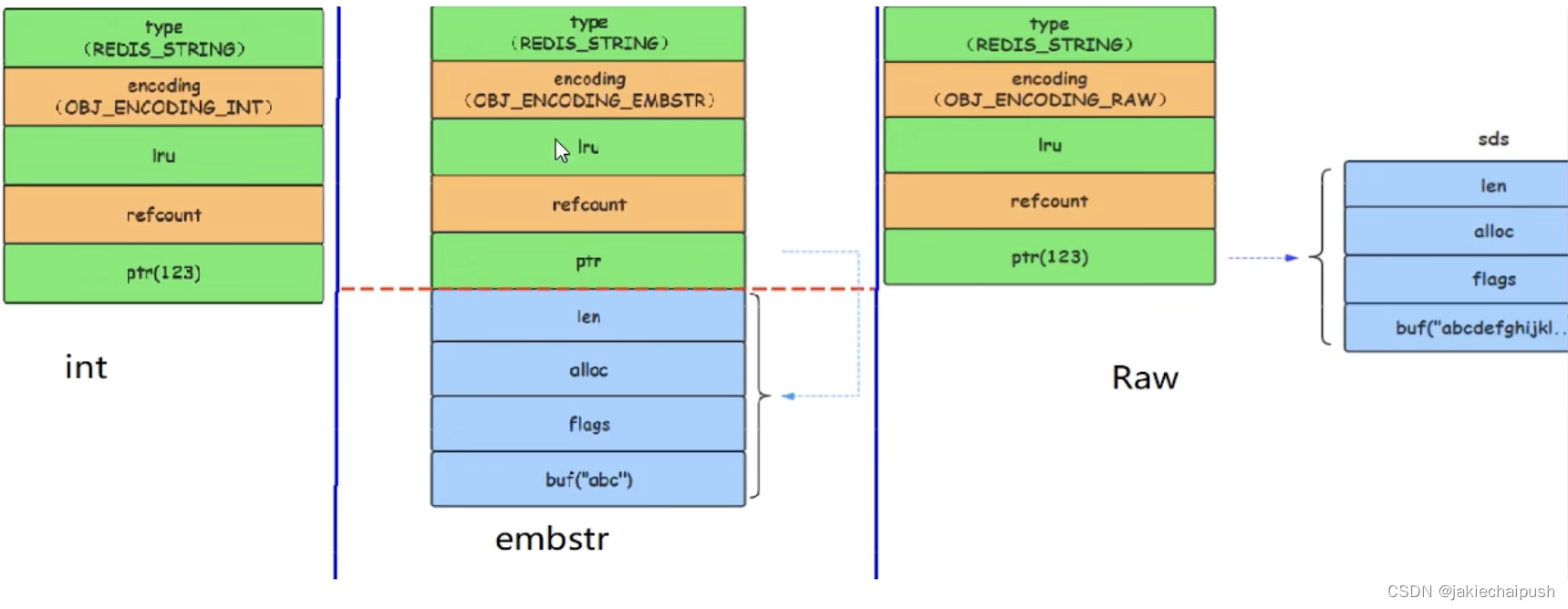
Redis底层数据结构之String
文章目录 1. 前提回顾2. RedisObject三大数据类型简介3. SDS字符串4. SDS字符串源码分析5. 总结 1. 前提回顾 前面我们说到redis的String数据结构在底层有多种编码方式。例如我们执行下面两条语句 set k1 v1 set age 17我们查看类型,发现这类型都是String类型 我们…...

【Maven学习笔记】Maven入门教程(适合新手反复观看学习)
Maven学习笔记 Maven的简要介绍Maven的安装和配置Maven的安装Maven安装的常用配置 Maven的使用入门编写pom编写主代码编写测试代码打包和运行使用Archetype生成项目骨架 Maven核心概念的阐述坐标案例分析依赖依赖的范围传递性依赖依赖范围依赖调节可选依赖Maven依赖常用的技巧 …...
idea Springboot 在线考试管理系统开发mysql数据库web结构java编程计算机网页
一、源码特点 springboot 在线考试管理系统是一套完善的完整信息系统,结合mvc框架和bootstrap完成本系统springboot spring mybatis ,对理解JSP java编程开发语言有帮助系统采用springboot框架(MVC模式开发),系统具有…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
