Vue3+TS+Vite 找不到模块“@/components/xxx/xxx”或其相应的类型声明
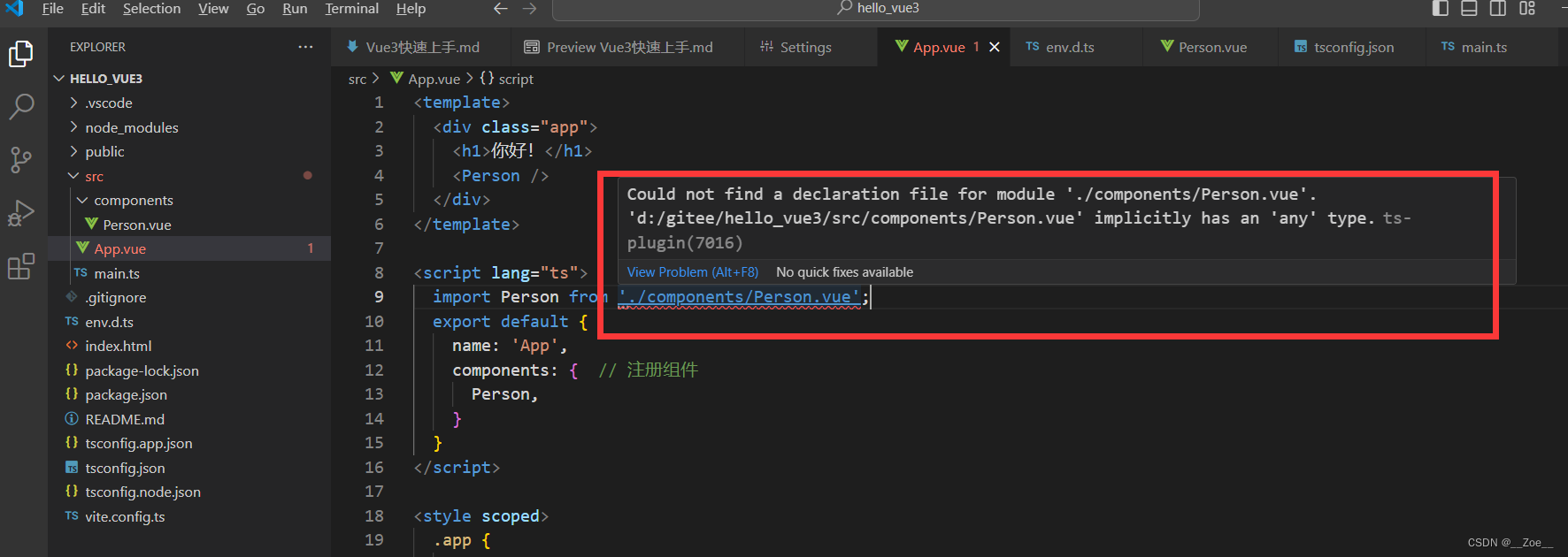引入vue文件时文件是存在的，引入路径也是对的，报找不到模块，有一些解决方案是在tsconfig.json里面做一些配置，大家可以自行百度（不知道是不是我百度的不对，我的没有解决）还有一种是在项目根目录建立一个 env.d.ts文件，写如下配置
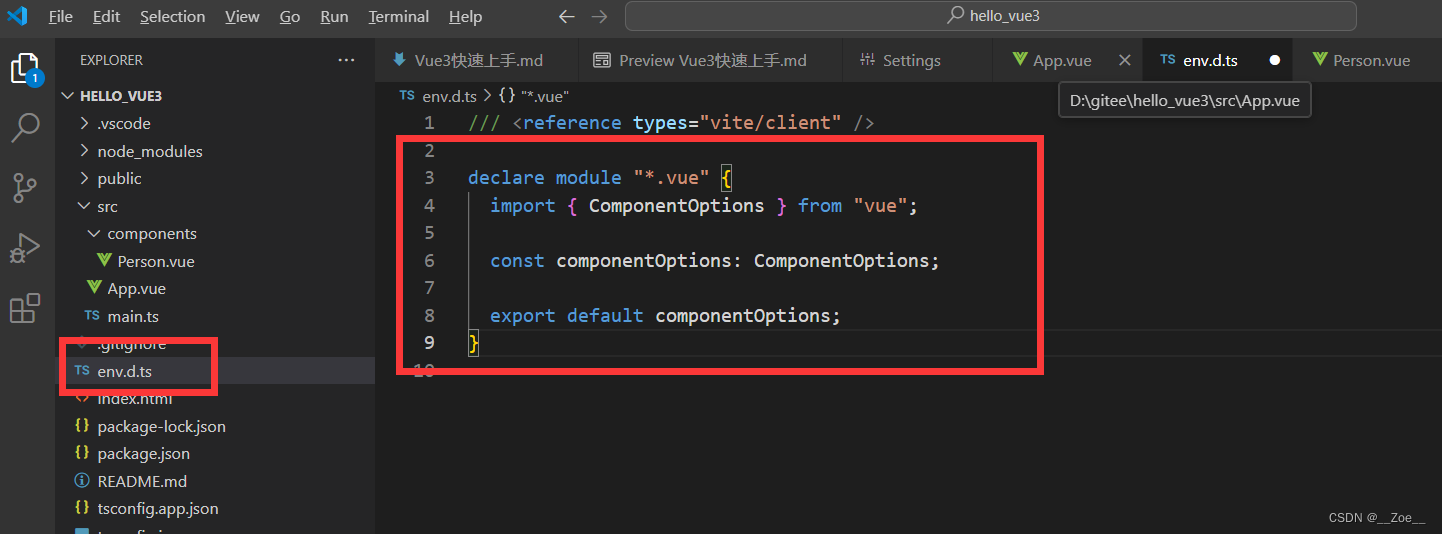
declare module "*.vue" {import { ComponentOptions } from "vue";const componentOptions: ComponentOptions;export default componentOptions;
}
参考链接：Vue3+TS+Vite 找不到模块“@/components/xxx/xxx”或其相应的类型声明。_vue.js_xiamengge-GitCode 开源社区
相关文章：
Vue3+TS+Vite 找不到模块“@/components/xxx/xxx”或其相应的类型声明
引入vue文件时文件是存在的，引入路径也是对的，报找不到模块，有一些解决方案是在tsconfig.json里面做一些配置，大家可以自行百度（不知道是不是我百度的不对，我的没有解决）还有一种是在项目根目录…...
Vue3-响应式基础:单文件和组合式文件
单文件：html <!DOCTYPE html> <html> <head><title>响应式基础</title> </head> <body><div id"app" ><!-- dynamic parameter:同样在指令参数上也可以使用一个 JavaScript 表达式，需要包…...
DVWA-File Upload文件上传
什么是文件上传漏洞？ 黑客利用文件上传后服务器解析处理文件的漏洞上传一个可执行的脚本文件，并通过此脚本文件获得了执行服务器端命令的能力。 造成文件上传漏洞的原因: 1.服务器配置不当 2.开源编辑器上传漏洞 3.本地文件上传限制被绕过 4.过滤不严格被…...
python之word操作
#pip install python-docx import docx import os pathos.path.abspath(__file__) file_pathos.path.join(path,"大题.docx") print(path) print(file_path) objdocx.Document("大题.docx") #第一个段落 p1obj.paragraphs[2] # print(p1.text) #所有段落 #…...
Linux下新增有root权限的用户
步骤： 1.以 root 用户身份登录到 CentOS 服务器。 2.使用以下命令创建新用户（将 newuser 替换为您想要创建的用户名）： sudo adduser username 3.为新用户设置密码： sudo passwd username 按照提示输入新增用户密码 …...
RPC通信原理（一）
RPC通信原理 RPC的概念 如果现在我有一个电商项目，用户要查询订单，自然而然是通过Service接口来调用订单的实现类。 我们把用户模块和订单模块都放在一起，打包成一个war包，然后再tomcat上运行，tomcat占有一个进程&am…...
修改/etc/resolve.conf重启NetworkManager之后自动还原
我ping 百度报错： [rootk8snode1 ~]# ping baidu.com ping: baidu.com: Name or service not known很明显，这是DNS解析问题。 于是我修改 /etc/resolv.conf 文件后，执行完sudo systemctl restart NetworkManager，/etc/resolv.con…...
Web前端依赖版本管理最佳实践
本文需要读者懂一点点前端的构建知识： 1. package.json文件的作用之一是管理外部依赖；2. .npmrc是npm命令默认配置，放在工程根目录。 Web前端构建一直都是一个不难，但是非常烦人的问题，在DevOps、CI/CD领域。 烦人的是…...
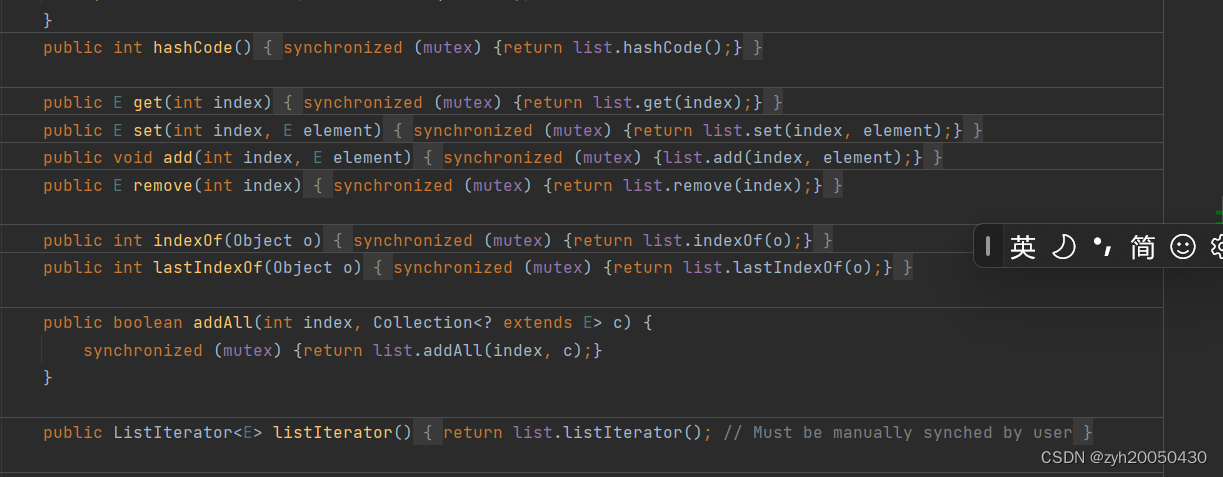
多线程进阶
一.常见的锁策略 这里所讲的锁，不是一把具体的锁，而是锁的特性 1.乐观锁和悲观锁 悲观乐观是对锁冲突大小的预测 若预测锁冲突概率不大，就可能会少一些工作，那就是乐观锁；反之就是悲观锁 总是假设最坏的情况&…...
总结linux常用命令
Linux常用命令总结如下： 文件与目录操作： ls：列出目录内容cd：改变当前目录pwd：显示当前工作目录mkdir：创建新目录cp：复制文件或目录rm：删除文件或目录mv：移动或重命名文件…...
C++ 枚举
C 枚举 5.4.1普通枚举 枚举的定义：，枚举类型是通过enum关键字定义的，比如定义颜色类型 enum Color {RED, // 默认值为0GREEN, // 默认值为1BLUE // 默认值为2 }; Color myColor RED;注意： （1）括…...
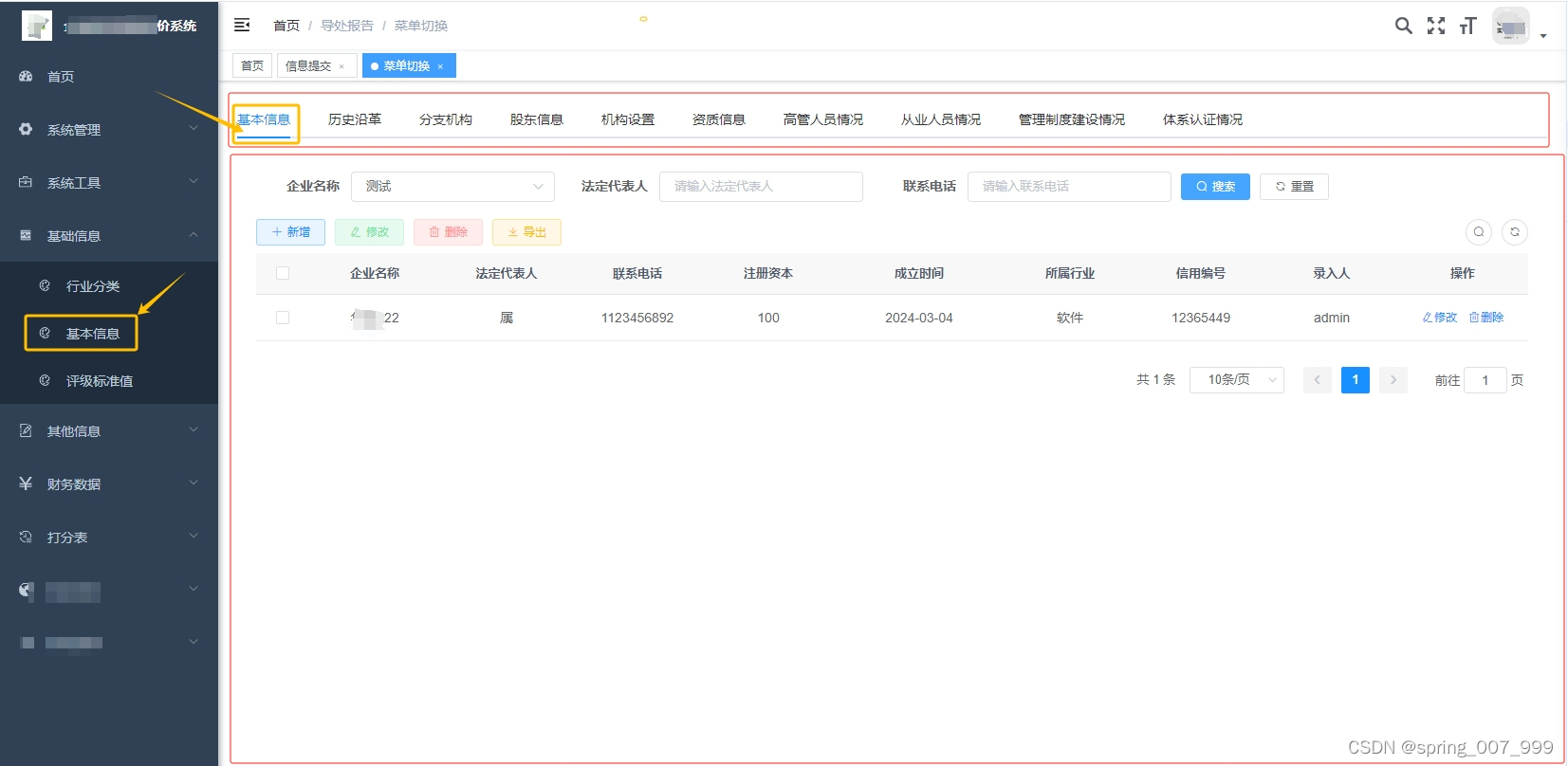
Vue2在一个页面内动态切换菜单显示对应的路由组件
项目的需求是在一个页面内动态获取导航菜单，导航菜单切换的时候显示对应的路由页面，类似于tab切换的形式，切换的导航菜单和页面左侧导航菜单是同一个路由组件，只是放到了一个页面上，显示的个数不同，所有是动…...
)
执行任务赚积分C卷(JavaPythonC++Node.jsC语言)
现有N个任务需要处理，同一时间只能处理一个任务，处理每个任务所需要的时间固定为1。 每个任务都有最晚处理时间限制和积分值，在最晚处理时间点之前处理完成任务才可获得对应的积分奖励。 可用于处理任务的时间有限，请问在有限的时间内，可获得的最多积分。 输入描述 第一…...
接口测试之文件下载
在工作中对于下载接口，经常会有这样的疑问：这类接口一般功能比较稳定，但是又比较重要，需要占用回归测试时间，有没有可替代的方式？ 答案肯定是有的，可以从接口测试/UI自动化测试介入，…...
算法思想总结：双指针算法
一、移动零 . - 力扣（LeetCode） 移动零 该题重要信息：1、保持非0元素的相对位置。2、原地对数组进行操作 思路：双指针算法 class Solution { public:void moveZeroes(vector<int>& nums){int nnums.size();for(int cur…...
python中的zip函数
1.zip（）同时迭代多个列表、字典等 使用zip()可以同时迭代多个可迭代对象，如列表、字典。 注意：当若干个可迭代对象的长度不相等时，zip()函数会停止在最短的可迭代对象。 例子： # 定义可迭代对象 numbers …...
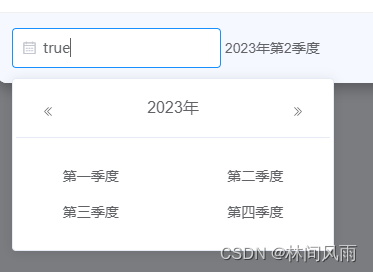
Element 选择季度组件
<template><el-dialogtitle"选择季度":show-close"false":close-on-click-modal"false":close-on-press-escape"false":visible"visiable"class"dialog list"append-to-body><div><div>&…...
4.MongoDB中16个常用CURD
基本的CURD 作为一个非专业的DBA，我们只需要会一些基本的curd就行，专业的内容还是需要专业的人去干的。CRUD 也就是增删改查，这是数据库最基本的功能，查询还支持全文检索，GEO 地理位置查询等。 01创建库 无需单独创…...
Tomcat数据源笔记
Tomcat数据源笔记 连接池的概念 连接池是一种由容器提供的机制，用于管理数据库连接对象的集合。连接池的主要作用是在应用程序需要与数据库进行交互时，提供可复用的连接对象，从而减少每次建立数据库连接的开销。 连接池的工作原理 连接池的…...
Spring-Kafka笔记整理
引入依赖<dependency><groupId>org.springframework.kafka</groupId><artifactId>spring-kafka</artifactId> </dependency>配置application.propertiesspring.kafka.bootstrap-servers192.168.99.51:9092编写kafka的配置类Configuration …...
【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现，玩家控制一个角色（龙）躲避障碍物（仙人掌和乌鸦）。以下是代码的详细介绍：…...
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张（Windows/Linux）
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况，可以通过以下几种方式模拟或触发： 1. 增加CPU负载 运行大量计算密集型任务，例如： 使用多线程循环执行复杂计算（如数学运算、加密解密等）。运行图…...
相机Camera日志分析之三十一：高通Camx HAL十种流程基础分析关键字汇总（后续持续更新中）
【关注我，后续持续新增专题博文，谢谢！！！】 上一篇我们讲了：有对最普通的场景进行各个日志注释讲解，但相机场景太多，日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志，通过下列分类关键字搜索，即可清晰的分析不同场景的相机运行流程差异…...
[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法，且在 O(n) 时间复杂度…...
)
OpenLayers 分屏对比(地图联动)
注：当前使用的是 ol 5.3.0 版本，天地图使用的key请到天地图官网申请，并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能，和卷帘图层不一样的是，分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型（LLM）的广泛应用，开发者常面临多个挑战： 各大模型（OpenAI、Claude、Gemini、Ollama）接口风格不统一；缺乏一个统一平台进行模型调用与测试；本地模型 Ollama 的集成与前…...
大语言模型（LLM）中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型（LLM）参数规模的增长，推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长，而KV缓存的内存消耗可能高达数十GB（例如Llama2-7B处理100K token时需50GB内存&a…...
【C++特殊工具与技术】优化内存分配(一)：C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时，性能会显著下降。以下是优化思路和简易实现方法： 一、核心优化思路 减少 JOIN 数量 数据冗余：添加必要的冗余字段（如订单表直接存储用户名）合并表：将频繁关联的小表合并成…...
C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如，已知表达式3*52，依照子表达式的求值顺序，有两种可能的结果，如图9-3所示。 如果乘法先执行，结果是17。如果5…...