服务器生产环境问题解决思路
游戏服务器开发节奏比较快,版本迭代很频繁,有一些项目甚至出现了周更新(每周准时停服更新维护)。由于功能开发时间短,研发人员本身技术能力等原因,线上出现bug很常见。笔者经历过的游戏项目,一年到头没几次更新不出现bug的(当然,配置问题也算bug)。那当出现bug,我们应该怎么处理呢?
1.处理线上bug的一般步骤
- 根据实际情况,可临时更新配置或者关闭功能入口,避免bug外溢,及时止损。
- 错误分析和定位:开发人员收集关于bug的详细信息,例如错误日志、报错信息等。QA人员需尽可能复现步骤。通过分析这些信息,可以了解到bug出现的原因和位置。
-
修复bug:根据错误分析的结果修复bug。这可能涉及到修改代码、调整配置等。确保修复后进行充分的测试,以确保bug已被解决。
-
重新部署:一旦bug修复完成,您需要将更新的代码、配置等重新部署(热部署)到游戏服务器上。确保重新部署的过程中不会中断游戏服务,以免影响用户体验。
-
监测和验证:重新部署后,您需要监测游戏服务器的运行情况,验证修复是否有效。使用监测工具或日志分析工具,观察系统的性能指标、错误日志等,以确保bug已经解决。
-
针对bug的后遗症进行脚本处理,如果有玩家获利,则回收道具;如果有玩家损失
相关文章:

服务器生产环境问题解决思路
游戏服务器开发节奏比较快,版本迭代很频繁,有一些项目甚至出现了周更新(每周准时停服更新维护)。由于功能开发时间短,研发人员本身技术能力等原因,线上出现bug很常见。笔者经历过的游戏项目,一年到头没几次更新不出现bug的(当然,配置问题也算bug)。那当出现bug,我们…...

鸿蒙Harmony应用开发—ArkTS声明式开发(容器组件:Column)
沿垂直方向布局的容器。 说明: 该组件从API Version 7开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 子组件 可以包含子组件。 接口 Column(value?: {space?: string | number}) 从API version 9开始,该接口…...
LLM之RAG实战(三十)| 探索RAG语义分块策略
在LLM之RAG实战(二十九)| 探索RAG PDF解析解析文档后,我们可以获得结构化或半结构化的数据。现在的主要任务是将它们分解成更小的块来提取详细的特征,然后嵌入这些特征来表示它们的语义,其在RAG中的位置如图1所示&…...

软件测试-------Web(性能测试 / 界面测试 / 兼容性测试 / 安全性测试)
Web(性能测试 / 界面测试 / 兼容性测试 / 安全性测试) 一、Web性能测试:(压力测试、负载测试、连接速度测试)1、压力测试: 并发测试 (如500人同时登录邮箱) 2、负载测试…...
)
工欲善其事,必先利其器,Markdown和Mermaid的梦幻联动(2)
该文章Github地址:https://github.com/AntonyCheng/typora-notes/tree/master/chapter03-mermaid 在此介绍一下作者开源的SpringBoot项目初始化模板(Github仓库地址:https://github.com/AntonyCheng/spring-boot-init-template & CSDN文…...

STM32基础--使用寄存器点亮流水灯
GPIO 简介 GPIO 是通用输入输出端口的简称,简单来说就是 STM32 可控制的引脚,STM32 芯片的 GPIO 引脚与外部设备连接起来,从而实现与外部通讯、控制以及数据采集的功能。STM32 芯片的 GPIO被分成很多组,每组有 16 个引脚…...
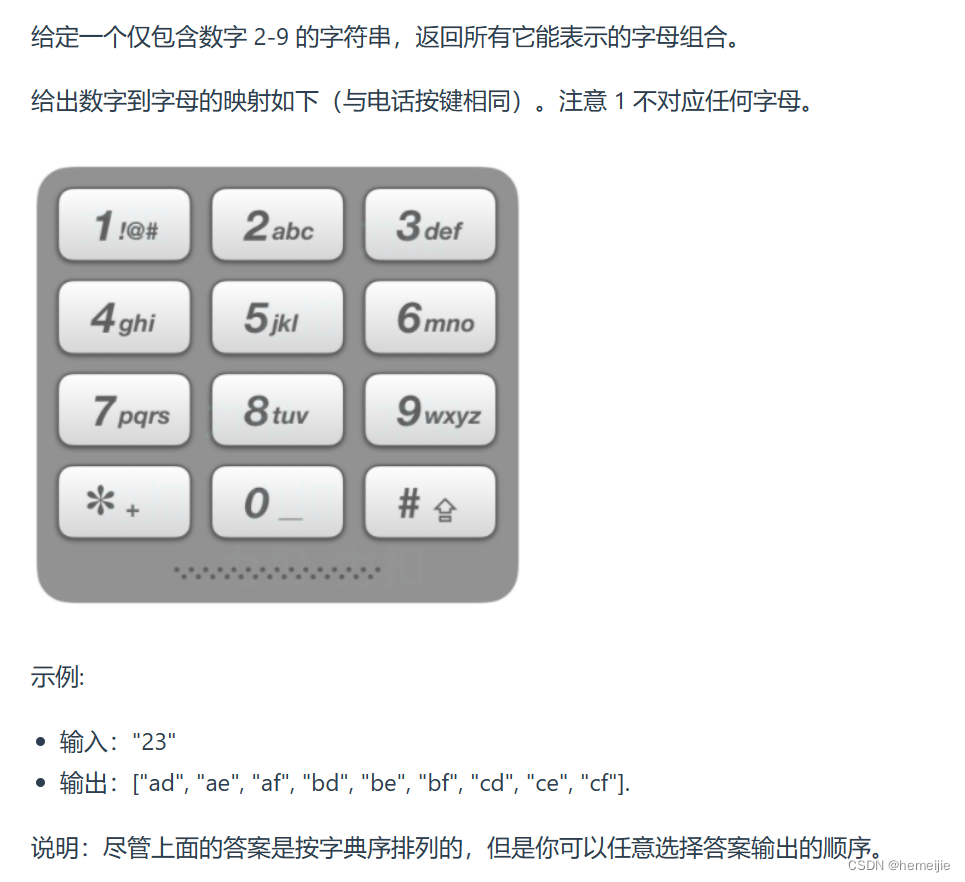
代码随想录训练营Day25:● 216.组合总和III ● 17.电话号码的字母组合
216.组合总和III 题目链接 https://leetcode.cn/problems/combination-sum-iii/description/ 题目描述 思路 自己写的效率会慢一些,而且没有用到剪枝 class Solution {List<List<Integer>> list new ArrayList<>();List<Integer> lis…...

SwiftUI的 特性 - ViewModify
SwiftUI的 特性 - ViewModify 记录一下SwiftUI的 特性 - ViewModify的使用方式 可以通过viewModify来管理视图的样式,结合extension来完成封装达到解偶效果 import SwiftUI/// 我们可以通过viewModify来管理视图的样式,来达到解偶效果 struct DefaultB…...
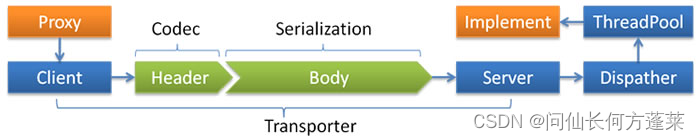
中间件 | RPC - [Dubbo]
INDEX 1 Dubbo 与 web 容器的关系2 注册发现流程3 服务配置3.1 注册方式 & 订阅方式3.2 服务导出3.3 配置参数 4 底层技术4.1 Dubbo 的 spi 机制4.2 Dubbo 的线程池4.3 Dubbo 的负载均衡策略4.3 Dubbo 的协议 1 Dubbo 与 web 容器的关系 dubbo 本质上是一个 RPC 框架&…...

【中等】保研/考研408机试-二叉树相关
目录 一、基本二叉树 1.1结构 1.2前序遍历(注意三种遍历中Visit所在的位置) 1.2中序遍历 1.3后序遍历 二、真题实战 2.1KY11 二叉树遍历(清华大学复试上机题)【较难】 2.2KY212 二叉树遍历二叉树遍历(华中科技大…...
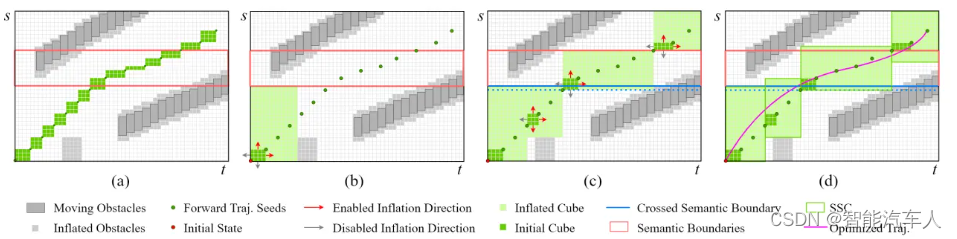
自动驾驶---Motion Planning之构建SLT Driving Corridor
1 背景 在上篇博客《自动驾驶---Motion Planning之Speed Boundary》中,主要介绍了Apollo中Speed Boundary的一些内容,可以构造ST图得到边界信息,最后结合粗糙的速度曲线和路径曲线,即可使用优化的方法求解得到最终的轨迹信息(s,s,s,l,l,l)。 本篇博客笔者主要介绍近…...
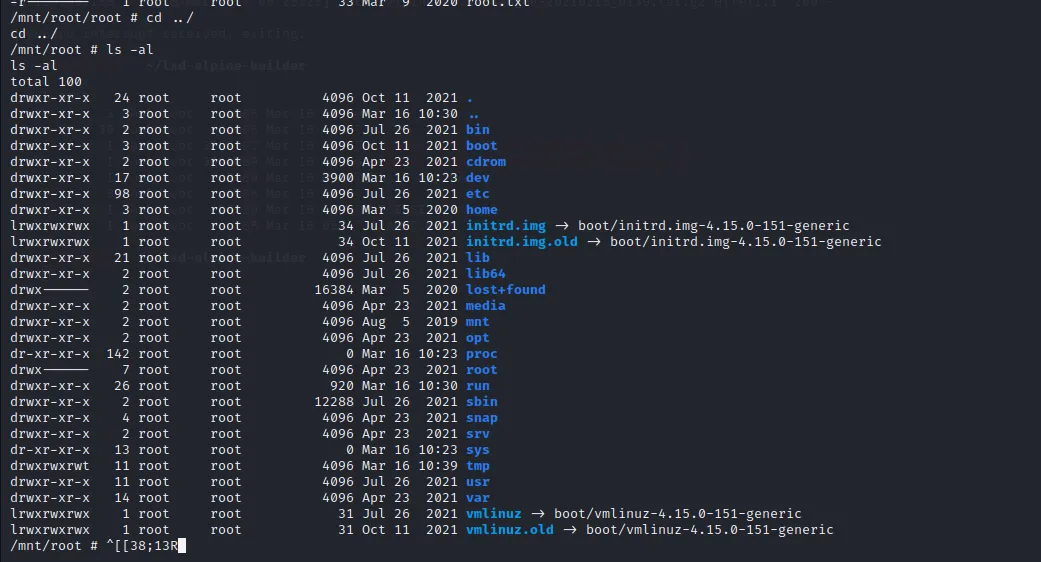
本地文件包含漏洞利用
目录 前期信息收集获取网站权限获取服务器权限纵向提权 前期信息收集 拿到目标的资产,先试一下IP能不能访问 探测一下目标的端口运行的是什么服务 nmap -sC -sV xx.xx9.95.185 -Pn获取网站权限 我们可以知道目标的80端口上运行着http服务,服务器是u…...
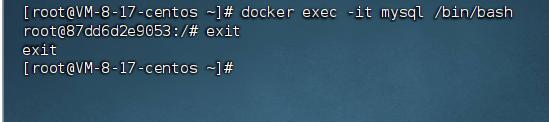
【docker】docker的常用命令
📝个人主页:五敷有你 🔥系列专栏:中间件 ⛺️稳中求进,晒太阳 常规命令 docker version #查看docker 版本信息docker info #显示docker 的系统信息,包括镜像和容器数量docker --help #查看所有的命…...

jmeter实战
jmeter学习 1,接口在定义时,post请求参数尽量放在body里面,get请求参数尽量放在parameters里面,否则会导致jmeter请求接口报错的问题(jmeter底层有较为严格的请求格式) 2,定义全局变量使用:Config Elemen…...

面试官常问问题
1、请你简单的自我介绍一下? 【Tips】① 口述内容不可与简历内容冲突;②阐述方式避免过度官方 且语速较快;③言简意赅,直击要害,抓重点突出项;④面试前应自己模拟练习几次,避免过度紧张导致的口…...
外包就干了2个月,技术退步明显....
先说情况,大专毕业,18年通过校招进入湖南某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...
)
面向对象 汇总(详细内容见Day12—16)
面向对象 汇总(详细内容见Day12—16) 文章目录 面向对象 汇总(详细内容见Day12—16)一、概念二、类三、对象四、成员属性/成员变量五、成员方法六、构造方法七、private - 私有化八、封装九、this - 本对象十、分包十一、static -…...

结构体联合体枚举和位段
文章目录 结构体结构体类型的声明特殊的声明 结构的自引用结构体变量的定义和初始化结构体内存对齐为什么要内存对齐结构体传参结构体实现位段(位段的填充&可移植性)位段位段的内存分配空间如何开辟位段的跨平台问题位段的应用 枚举枚举类型的定义枚…...

人类程序员真要失业?首位“AI软件工程师”亮相引爆科技圈
初创公司Cognition成立不到两个月,但已经拥有十名天才工程师。他们推出了一款名为Devin的人工智能(AI)助手,可以协助人类软件工程师完成各种开发任务。Devin与现有的其他AI编码者不同,它能够从头开始构建网站、自动部署…...

redis的过期策略以及内存淘汰机制
redis采用的是定期删除惰性删除策略。 为什么不用定时删除策略? 定时删除,用一个定时器来负责监视key,过期则自动删除。虽然内存及时释放,但是十分消耗CPU资源。在大并发请求下,CPU要 将时间应用在处理请求,而不是删除key,因此没有采用这一策…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
