数据清洗与预处理:打造高质量数据分析基础
随着数据的快速增长,数据分析已经成为企业和组织的核心业务。然而,原始数据往往包含各种杂质和异常,这就需要我们进行数据清洗和预处理,以确保分析结果的准确性和可靠性。
1. 数据清洗的重要性:
数据清洗是指对原始数据进行检查、修正和完善,以消除错误、不一致性和噪声,提高数据质量和可信度。其重要性体现在以下几个方面:
确保数据质量: 高质量的数据清洗可以消除数据中的错误和不一致性,提高数据的准确性和可信度。
降低分析风险: 清洗后的数据更加干净,可以减少因数据质量问题而引发的分析风险。
提高分析效率: 清洗过的数据更易于理解和分析,可以节省分析人员的时间和精力成本。
2. 常见数据问题及解决方法:
在进行数据清洗时,我们常常会遇到缺失值、异常值和重复值等问题。下面将介绍这些问题的解决方法,并通过实例演示:
缺失值处理: 缺失值是指数据表中某些字段缺少数值或信息的情况。处理方法包括删除缺失值、填充缺失值和插值等。例如,在一份销售数据中,如果某一行的销售日期缺失,我们可以根据其他字段的信息来填充或者删除该行数据。
异常值检测与处理: 异常值是指与大多数观测值显著不同的数据点。处理方法包括基于统计方法和机器学习算法的异常值检测与修正。例如,通过
相关文章:

数据清洗与预处理:打造高质量数据分析基础
随着数据的快速增长,数据分析已经成为企业和组织的核心业务。然而,原始数据往往包含各种杂质和异常,这就需要我们进行数据清洗和预处理,以确保分析结果的准确性和可靠性。 1. 数据清洗的重要性: 数据清洗是指对原始数据进行检查、修正和完善,以消除错误、不一致性和噪声…...
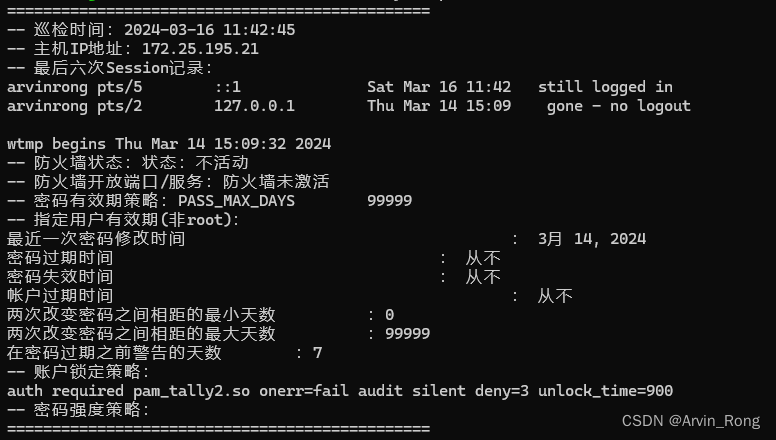
Linux服务器(Debian系)包含UOS安全相关巡检shell脚本
#!/bin/bash# Define output file current_date$(date "%Y%m%d") # Gets the current date in YYYYMMDD format output_file"server_security_inspection_report_${current_date}.txt"# Empty the file initially echo > $output_file# 获取巡检时间 (…...

BS4网络提取selenium.chrome.WebDriver类的方法及属性
BS4网络提取selenium.chrome.WebDriver类的方法及属性 chrome.webdriver: selenium.webdriver.chrome.webdriver — Selenium 4.18.1 documentation class selenium.webdriver.chrome.webdriver.WebDriver 是 Selenium 中用于操作 Chrome 浏览器的 WebDriver 类。WebDriver 类…...

Prompt Engineering(提示工程)
Prompt 工程简介 在近年来,大模型(Large Model)如GPT、BERT等在自然语言处理领域取得了巨大的成功。这些模型通过海量数据的训练,具备了强大的语言理解和生成能力。然而,要想充分发挥这些大模型的潜力,仅仅…...

移远通信亮相AWE 2024,以科技力量推动智能家居产业加速发展
科技的飞速发展,为我们的生活带来了诸多便利,从传统的家电产品到智能化的家居设备,我们的居家生活正朝着更智能、更便捷的方向变革。 3月14日,中国家电及消费电子博览会(Appliance&electronics World Expo…...

Java中上传数据的安全性探讨与实践
✨✨谢谢大家捧场,祝屏幕前的小伙伴们每天都有好运相伴左右,一定要天天开心哦!✨✨ 🎈🎈作者主页: 喔的嘛呀🎈🎈 目录 引言 一. 文件上传的风险 二. 使用合适的框架和库 1. Spr…...

Leetcode 17. 电话号码的字母组合
心路历程: 之前看过这道题的解法但是忘了。一开始想多重循环遍历,发现不知道写几个for循环,于是想到递归;发现递归需要记录选择的路径而不是返回节点值,想到了回溯。 回溯的解题模板:维护两个变量…...

蓝桥杯单片机快速开发笔记——独立键盘
一、原理分析 二、思维导图 三、示例框架 #include "reg52.h" sbit S7 P3^0; sbit S6 P3^1; sbit S5 P3^2; sbit S4 P3^3; void ScanKeys(){if(S7 0){Delay(500);if(S7 0){while(S7 0);}}if(S6 0){Delay(500);if(S6 0){while(S6 0)…...
Swift 面试题及答案整理,最新面试题
Swift 中如何实现单例模式? 在Swift中,单例模式的实现通常采用静态属性和私有初始化方法来确保一个类仅有一个实例。具体做法是:定义一个静态属性来存储这个单例实例,然后将类的初始化方法设为私有,以阻止外部通过构造…...

微信小程序上传图片c# asp.net mvc端接收案例
在微信小程序上传图片到服务器,并在ASP.NET MVC后端接收这个图片,可以通过以下步骤实现: 1. 微信小程序端 首先,在微信小程序前端,使用 wx.chooseImage API 选择图片,然后使用 wx.uploadFile API 将图片上…...

57、服务攻防——应用协议RsyncSSHRDP漏洞批扫口令猜解
文章目录 口令猜解——Hydra-FTP&RDP&SSH配置不当——未授权访问—Rsync文件备份协议漏洞——应用软件-FTP&Proftpd搭建 口令猜解——Hydra-FTP&RDP&SSH FTP:文本传输协议,端口21;RDP:windows上远程终端协议…...

java:Druid工具类解析sql获取表名
java:Druid工具类解析sql获取表名 1 前言 alibaba的druid连接池除了sql执行的功能外,还有sql语法解析的工具提供,参考依赖如下: <dependency><groupId>com.alibaba</groupId><artifactId>druid</ar…...

MySQL--深入理解MVCC机制原理
什么是MVCC? MVCC全称 Multi-Version Concurrency Control,即多版本并发控制,维持一个数据的多个版本,主要是为了提升数据库的并发访问性能,用更高性能的方式去处理数据库读写冲突问题,实现无锁并发。 什…...

数据挖掘简介与应用领域概述
数据挖掘,作为信息技术领域中的重要分支之一,旨在从大量数据中发现潜在的模式、关联和趋势,以提取有用的信息和知识。在信息爆炸时代,大量数据的积累成为了常态,数据挖掘技术的出现填补了人们处理这些数据的空白&#…...
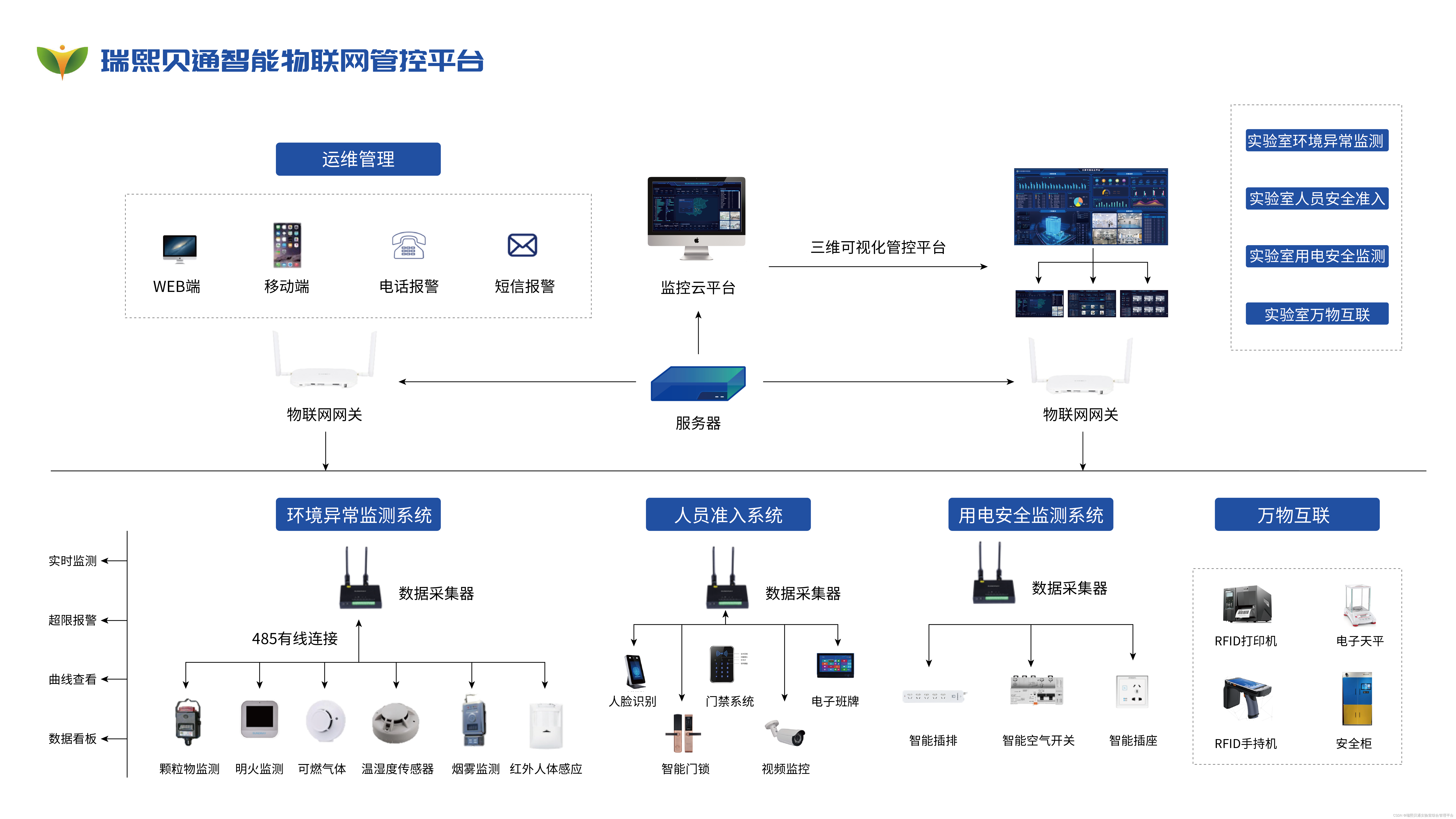
瑞熙贝通打造智慧校园实验室安全综合管理平台
一、建设思路 瑞熙贝通实验室安全综合管理平台是基于以实验室安全,用现代化管理思想与人工智能、大数据、互联网技术、物联网技术、云计算技术、人体感应技术、语音技术、生物识别技术、手机APP、自动化仪器分析技术有机结合,通过建立以实验室为中心的管…...

openstack调整虚拟机CPU 内存 磁盘 --来自gpt
在OpenStack中调整虚拟机(即实例)的CPU、内存(RAM)和磁盘大小通常涉及到以下几个步骤:首先,确定你要修改的实例名称或ID;其次,根据需要调整的资源类型,使用相应的命令进行…...
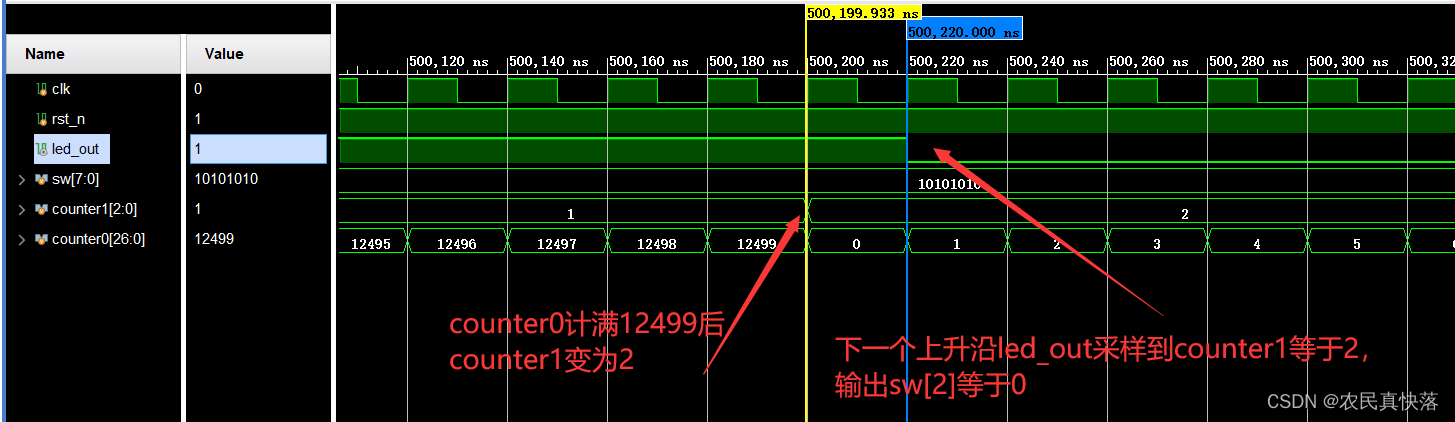
【IC设计】Verilog线性序列机点灯案例(三)(小梅哥课程)
声明:案例和代码来自小梅哥课程,本人仅对知识点做做笔记,如有学习需要请支持官方正版。 文章目录 该系列目录设计目标设计思路RTL及Testbench代码RTL代码Testbench代码 仿真结果上板视频 该系列目录 Verilog线性序列机点灯案例(一)ÿ…...

【打工日常】使用Docker部署团队协作文档工具
一、ShowDoc介绍 ShowDoc是一个适合IT团队共同协作API文档、技术文档的工具。通过showdoc,可以方便地使用markdown语法来书写出API文档、数据字典文档、技术文档、在线excel文档等等。 响应式网页设计:可将项目文档分享到电脑或移动设备查看。同时也可…...
(一)Neo4j下载安装以及初次使用
(一)下载 官网地址:Neo4j Graph Database & AnamConnect data as its stored with Neo4j. Perform powerful, complex queries at scale and speed with our graph data platform.https://neo4j.com/ (二)安装并配…...

QT for Mcu的学习建议
QT for MCU(微控制器单元)是一个相对较新的领域,它允许在资源受限的微控制器上运行Qt框架,从而为嵌入式设备带来丰富的用户界面和跨平台的开发体验。以下是一些建议,可以帮助你开始学习Qt for MCU: 理解Qt…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
