广义状态平均法功率变换器建模分析
两种状态平均法在功率变换器建模的应用比较
[!info] Bibliography
[1] 高朝晖, 林辉张晓斌 & 吴小华, “两种状态平均法在功率变换器建模的应用比较,” 计算机仿真, no. 241-244+248, 2008.
[!note]
状态空间平均法采用直流量近似(线性系统模型),广义状态空间平均采用直流量和基波分量近似。也即状态空间平均法采用0阶傅里叶级数近似,广义状态空间平均采用0阶和1阶傅里叶级数近似
应用状态空间平均法分析 Buck变换器
广义状态平均法(GSSA)
广义状态平均采用傅里叶级数拟合系统状态:
x(t)=∑n=−∞∞⟨x⟩n(t)ejnωtx(t) = \sum_{n = -\infty}^\infty \langle x \rangle_n(t) e^{j n \omega t} x(t)=n=−∞∑∞⟨x⟩n(t)ejnωt
- ω=2π/T\omega = 2\pi / Tω=2π/T
⟨x⟩n(t)\langle x \rangle_n(t)⟨x⟩n(t) 代表傅里叶系数:
⟨x⟩n(t)=1T∫t−Ttx(τ)e−jnωτdτ\langle x \rangle_n(t) = \frac 1T \int_{t-T}^t x(\tau) e^{-j n \omega \tau}d\tau ⟨x⟩n(t)=T1∫t−Ttx(τ)e−jnωτdτ
- nnn is AKA index-k average
三角形式傅里叶级数:
x(τ)=⟨x⟩0+2∑n=1∞(a1cos(nωτ)+b1sin(nωτ))x(\tau)=\langle x\rangle_0+2 \sum_{n=1}^{\infty}\left(a_1 \cos (n \omega \tau) + b_1 \sin (n \omega \tau)\right) x(τ)=⟨x⟩0+2n=1∑∞(a1cos(nωτ)+b1sin(nωτ))
- ⟨x⟩n(t)=an−jbn\langle x\rangle_n(t) = a_n - j b_n⟨x⟩n(t)=an−jbn
an=12π∫02πx(ωτ)cos(ωτ)d(ωτ)bn=12π∫02πx(ωτ)sin(ωτ)d(ωτ)⟨x⟩0=1T∫t−Ttx(τ)dτ\begin{aligned} {a}_n &=\frac{1}{2 \pi} \int_0^{2 \pi} {x}(\omega \tau) \cos (\omega \tau) \mathrm{d}(\omega \tau) \\ {b}_n &=\frac{1}{2 \pi} \int_0^{2 \pi} {x}(\omega \tau) \sin (\omega \tau) \mathrm{d}(\omega \tau) \\ \langle{x}\rangle_0 &=\frac{1}{{T}} \int_{t-{T}}^t {x}(\tau) \mathrm{d} \tau \end{aligned} anbn⟨x⟩0=2π1∫02πx(ωτ)cos(ωτ)d(ωτ)=2π1∫02πx(ωτ)sin(ωτ)d(ωτ)=T1∫t−Ttx(τ)dτ
性质:
-
d⟨x⟩n(t)dt=⟨dxdt⟩n(t)−jnω⟨x⟩n(t)\frac{d \langle x\rangle_n(t)}{d t}=\left\langle\frac{d x}{d t}\right\rangle_n(t)-j n \omega\langle x\rangle_n(t)dtd⟨x⟩n(t)=⟨dtdx⟩n(t)−jnω⟨x⟩n(t)
[!note] Proof
⟨x⟩n(t)=1T∫0Tx(t−T+s)e−jnω(t−T+s)ds\langle x \rangle_n(t) = \frac1T \int_0^T x(t - T + s) e^{-j n \omega(t-T+s)}ds⟨x⟩n(t)=T1∫0Tx(t−T+s)e−jnω(t−T+s)ds
-
⟨qx⟩n=∑i=−∞∞⟨q⟩n−i⟨x⟩i\langle qx \rangle_n = \sum_{i = -\infty}^\infty \langle q \rangle_{n -i} \langle x \rangle_i⟨qx⟩n=∑i=−∞∞⟨q⟩n−i⟨x⟩i
Suppose that x(t)x(t)x(t) and q(t)q(t)q(t) can be approximated by 0- and 1-order Fourier series (即直流和基波量):
q(t)≈⟨q⟩0+⟨q⟩−1e−jωt+⟨q⟩1ejωtx(t)≈⟨x⟩0+⟨x⟩−1e−jωt+⟨x⟩1ejωt\begin{aligned} q(t) &\approx \langle q \rangle_0 + \langle q \rangle_{-1} e^{- j \omega t} + \langle q \rangle_1 e^{j \omega t} \\ x(t) &\approx \langle x \rangle_0 + \langle x \rangle_{-1} e^{- j \omega t} + \langle x \rangle_1 e^{j \omega t} \end{aligned} q(t)x(t)≈⟨q⟩0+⟨q⟩−1e−jωt+⟨q⟩1ejωt≈⟨x⟩0+⟨x⟩−1e−jωt+⟨x⟩1ejωt
[!note]
这里注意,三角形式傅里叶级数中的直流和基波项(a0/2+a1cos(ωt)+b1sin(ωt)a_0/2 + a_1 \cos(\omega t) + b_1 \sin(\omega t)a0/2+a1cos(ωt)+b1sin(ωt))对应于复数形式的傅立叶级数中 000、±1±1±1次项(c0+c−1e−iωt+c1eiωtc_0 + c_{-1}e^{-i \omega t}+ c_{1} e^{i\omega t}c0+c−1e−iωt+c1eiωt)
xxx 和 qqq 乘积可表示为:
⟨qx⟩0=⟨q⟩0⟨x⟩0+⟨q⟩−1⟨x⟩1+⟨q⟩1⟨x⟩−1⟨qx⟩1=⟨q⟩0⟨x⟩1+⟨q⟩1⟨x⟩0⟨qx⟩−1=⟨q⟩0⟨x⟩−1+⟨q⟩−1⟨x⟩0\begin{aligned} \langle qx \rangle_0 &= \langle q \rangle_0 \langle x \rangle_0 + \langle q \rangle_{-1} \langle x \rangle_1 + \langle q \rangle_1 \langle x \rangle_{-1} \\ \langle qx \rangle_1 &= \langle q \rangle_0 \langle x \rangle_1 + \langle q \rangle_{1} \langle x \rangle_0\\ \langle qx \rangle_{-1} &= \langle q \rangle_0 \langle x \rangle_{-1} + \langle q \rangle_{-1} \langle x \rangle_0 \end{aligned} ⟨qx⟩0⟨qx⟩1⟨qx⟩−1=⟨q⟩0⟨x⟩0+⟨q⟩−1⟨x⟩1+⟨q⟩1⟨x⟩−1=⟨q⟩0⟨x⟩1+⟨q⟩1⟨x⟩0=⟨q⟩0⟨x⟩−1+⟨q⟩−1⟨x⟩0
正负平均指数互为共轭⟨x⟩1=⟨x⟩−1∗\langle x \rangle_1 = \langle x \rangle_{-1}^*⟨x⟩1=⟨x⟩−1∗
- ⟨q⟩1=⟨q⟩1R+j⟨q⟩1I=⟨q⟩−1∗=(⟨q⟩−1R+⟨q⟩−1I)∗\langle q \rangle_1 = \langle q \rangle_1^R + j \langle q \rangle_1^I = \langle q \rangle_{-1}^* = \left(\langle q \rangle_{-1}^R + \langle q \rangle_{-1}^I\right)^*⟨q⟩1=⟨q⟩1R+j⟨q⟩1I=⟨q⟩−1∗=(⟨q⟩−1R+⟨q⟩−1I)∗
- ⟨x⟩1=⟨x⟩1R+j⟨x⟩1I=⟨x⟩−1∗=(⟨x⟩−1R+⟨x⟩−1I)∗\langle x \rangle_1 = \langle x \rangle_1^R + j \langle x \rangle_1^I = \langle x \rangle_{-1}^* = \left(\langle x \rangle_{-1}^R + \langle x \rangle_{-1}^I\right)^*⟨x⟩1=⟨x⟩1R+j⟨x⟩1I=⟨x⟩−1∗=(⟨x⟩−1R+⟨x⟩−1I)∗
于是
⟨qx⟩0=⟨q⟩0⟨x⟩0+2(⟨q⟩1R⟨x⟩1R+⟨q⟩1I⟨x⟩1I)⟨qx⟩1R=⟨q⟩0⟨x⟩1R+⟨q⟩1R⟨x⟩0⟨qx⟩1I=⟨q⟩0⟨x⟩1I+⟨q⟩1I⟨x⟩0\begin{aligned} \langle qx \rangle_0 &= \langle q \rangle_0 \langle x \rangle_0 + 2\left(\langle q \rangle_{1}^R \langle x \rangle_1^R + \langle q \rangle_1^I \langle x \rangle_{1}^I\right) \\ \langle qx \rangle_1^R &= \langle q \rangle_0 \langle x \rangle_1^R + \langle q \rangle_{1}^R \langle x \rangle_0\\ \langle qx \rangle_{1}^I &= \langle q \rangle_0 \langle x \rangle_{1}^I + \langle q \rangle_{1}^I \langle x \rangle_0 \end{aligned} ⟨qx⟩0⟨qx⟩1R⟨qx⟩1I=⟨q⟩0⟨x⟩0+2(⟨q⟩1R⟨x⟩1R+⟨q⟩1I⟨x⟩1I)=⟨q⟩0⟨x⟩1R+⟨q⟩1R⟨x⟩0=⟨q⟩0⟨x⟩1I+⟨q⟩1I⟨x⟩0
GSSA 建模 BUCK
定义开关函数
q(t)={0关1开q(t) =\left\{ \begin{matrix} 0 & 关 \\ 1 & 开 \end{matrix} \right. q(t)={01关开
BUCK system model:
LdiLdt=vinq(t)−voCdvodt=iL−voR\begin{aligned} & L \frac{d {i_L}}{d t}=v_{i n} q(t)-v_o \\ & C \frac{d v_o}{d t}=i_L-\frac{v_o}{R} \end{aligned} LdtdiL=vinq(t)−voCdtdvo=iL−Rvo
0 平均指数模型:
Ld⟨iL⟩0dt=Vin⟨q⟩0−⟨vo⟩0Cd⟨vo⟩0dt=⟨iL⟩0−⟨vo⟩0R\begin{aligned} & L\frac{d\langle i_L\rangle_0}{dt}=V_{in} \langle q \rangle_0 - \langle v_o \rangle_0 \\ & C\frac{d\langle v_o\rangle_0}{dt}=\langle{i_L}\rangle_0-\frac{\left\langle\mathrm{v}_o\right\rangle_0}{{R}} \end{aligned} Ldtd⟨iL⟩0=Vin⟨q⟩0−⟨vo⟩0Cdtd⟨vo⟩0=⟨iL⟩0−R⟨vo⟩0
1平均指数模型:
d⟨iL⟩1dt=−jω⟨iL⟩1+1L(Vin⟨q⟩1−⟨vo⟩1)d⟨vo⟩1dt=−jω⟨vo⟩1+1C(⟨iL⟩0−⟨vo⟩0R)\begin{aligned} \frac{d\langle i_L\rangle_1}{dt} &= -j\omega \langle i_L\rangle_1 + \frac1L \left( V_{in} \langle q \rangle_1 - \langle v_o \rangle_1 \right)\\ \frac{d\langle v_o\rangle_1}{dt} &= -j\omega \langle v_o \rangle_1 + \frac 1C \left( \langle{i_L}\rangle_0-\frac{\left\langle\mathrm{v}_o\right\rangle_0}{{R}} \right) \end{aligned} dtd⟨iL⟩1dtd⟨vo⟩1=−jω⟨iL⟩1+L1(Vin⟨q⟩1−⟨vo⟩1)=−jω⟨vo⟩1+C1(⟨iL⟩0−R⟨vo⟩0)
考虑共轭关系,1平均指数模型的实部虚部分别可以写作:
d⟨iL⟩1Rdt=ω⟨iL⟩1I+1L(Vin⟨q⟩1R−⟨vo⟩1R)d⟨iL⟩1Idt=−ω⟨iL⟩1R+1L(Vin⟨q⟩1I−⟨vo⟩1I)d⟨vo⟩1Rdt=ω⟨vo⟩1I+1C(⟨iL⟩1R−⟨vo⟩1RR)d⟨vo⟩1Idt=−ω⟨vo⟩1R+1C(⟨iL⟩1I−⟨vo⟩1IR)\begin{aligned} \frac{d\langle i_L\rangle_1^R}{dt} &= \omega \langle i_L\rangle_1^I + \frac1L \left( V_{in} \langle q \rangle_1^R - \langle v_o \rangle_1^R \right)\\ \frac{d\langle i_L\rangle_1^I}{dt} &= -\omega \langle i_L\rangle_1^R + \frac1L \left( V_{in} \langle q \rangle_1^I - \langle v_o \rangle_1^I \right)\\ \frac{d\langle v_o\rangle_1^R}{dt} &= \omega \langle v_o \rangle_1^I + \frac 1C \left( \langle{i_L}\rangle_1^R-\frac{\left\langle\mathrm{v}_o\right\rangle_1^R}{{R}} \right)\\ \frac{d\langle v_o\rangle_1^I}{dt} &= -\omega \langle v_o \rangle_1^R + \frac 1C \left( \langle{i_L}\rangle_1^I -\frac{\left\langle\mathrm{v}_o\right\rangle_1^I}{{R}} \right) \end{aligned} dtd⟨iL⟩1Rdtd⟨iL⟩1Idtd⟨vo⟩1Rdtd⟨vo⟩1I=ω⟨iL⟩1I+L1(Vin⟨q⟩1R−⟨vo⟩1R)=−ω⟨iL⟩1R+L1(Vin⟨q⟩1I−⟨vo⟩1I)=ω⟨vo⟩1I+C1(⟨iL⟩1R−R⟨vo⟩1R)=−ω⟨vo⟩1R+C1(⟨iL⟩1I−R⟨vo⟩1I)
选取状态变量x=[⟨iL⟩1R,⟨iL⟩1I,⟨vo⟩1R,⟨vo⟩1I,⟨iL⟩0R,⟨vo⟩0R]Tx = [\langle i_L\rangle_1^R, \langle i_L\rangle_1^I, \langle v_o \rangle_1^R, \langle v_o \rangle_1^I,\langle i_L \rangle_0^R, \langle v_o \rangle_0^R]^Tx=[⟨iL⟩1R,⟨iL⟩1I,⟨vo⟩1R,⟨vo⟩1I,⟨iL⟩0R,⟨vo⟩0R]T, 可以得到状态空间方程:
x˙=Ax+Bu\begin{aligned} \dot x &= Ax + Bu\\ \end{aligned} x˙=Ax+Bu
- A=[0ω−1/L000−ω00−1/L001/C0−1/(RC)ω0001/C−ω−1/(RC)0000000−1/L00001/C−1/(RC)]A = \left[\begin{matrix} 0 & \omega & -1/L &0 & 0&0 \\ -\omega & 0 & 0 & -1/L & 0 & 0\\ 1/C & 0 & -1/(RC) & \omega & 0 & 0\\ 0 & 1/C & -\omega & -1/(RC) & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & -1/L \\ 0 & 0 & 0 & 0 & 1/C & -1 / (RC) \end{matrix}\right]A=0−ω1/C000ω001/C00−1/L0−1/(RC)−ω000−1/Lω−1/(RC)00000001/C0000−1/L−1/(RC)
- B=[⟨q⟩1RL,⟨q⟩1IL,0,0,⟨q⟩0L,0]TB = \left[\frac{\langle q \rangle_1^R}L, \frac{\langle q \rangle_1^I}L, 0, 0, \frac{\langle q \rangle_0}L,0 \right]^TB=[L⟨q⟩1R,L⟨q⟩1I,0,0,L⟨q⟩0,0]T
- u=Vinu = V_{in}u=Vin
开关函数 q(t)q(t)q(t) 的 0 阶和 1 阶傅里叶系数:
⟨q⟩1R=12π∫02πDcos(ωτ)d(ωτ)=12πsin(2πD)⟨q⟩1I=−12π∫02πDsin(ωτ)d(ωτ)=12π[cos(2πD)−1]⟨q⟩0=D\begin{aligned} \langle q \rangle_1^R &= \frac 1{2\pi} \int_0^{2\pi D} \cos (\omega \tau ) d(\omega \tau) = \frac1{2\pi} \sin (2\pi D)\\\langle q \rangle_1^I &= -\frac 1{2\pi} \int_0^{2\pi D} \sin (\omega \tau ) d(\omega \tau) = \frac1{2\pi} [\cos (2\pi D) - 1]\\ \langle q \rangle_0 &= D\\ \end{aligned} ⟨q⟩1R⟨q⟩1I⟨q⟩0=2π1∫02πDcos(ωτ)d(ωτ)=2π1sin(2πD)=−2π1∫02πDsin(ωτ)d(ωτ)=2π1[cos(2πD)−1]=D
根据广义状态模型的解 xxx,可以得到系统输出为
iL=2x1cos(ωt)−2x2sin(ωt)+x5vo=2x3cos(ωt)−2x4sin(ωt)+x6\begin{aligned} i_L &= 2x_1 \cos (\omega t) - 2x_2 \sin (\omega t) + x_5\\ v_o &= 2x_3 \cos (\omega t) - 2x_4 \sin (\omega t) + x_6\\ \end{aligned} iLvo=2x1cos(ωt)−2x2sin(ωt)+x5=2x3cos(ωt)−2x4sin(ωt)+x6
namely:
iL=2⟨iL⟩1Rcos(ωt)−2⟨iL⟩1Isin(ωt)+⟨iL⟩0vo=2⟨vo⟩1Rcos(ωt)−2⟨vo⟩1Isin(ωt)+⟨vo⟩0\begin{aligned} i_L &= 2\langle i_L \rangle_1^R \cos (\omega t) - 2\langle i _L\rangle_1^I \sin (\omega t) + \langle i_L\rangle_0\\ v_o &= 2\langle v_o \rangle_1^R \cos (\omega t) - 2\langle v_o \rangle_1^I \sin (\omega t) + \langle v_o \rangle_0\\ \end{aligned} iLvo=2⟨iL⟩1Rcos(ωt)−2⟨iL⟩1Isin(ωt)+⟨iL⟩0=2⟨vo⟩1Rcos(ωt)−2⟨vo⟩1Isin(ωt)+⟨vo⟩0
另外,普通状态平均的解其实是
iLSSA=x5,voSSA=x6i_{L_{SSA}} = x_5, v_{o_{SSA}} = x_6 iLSSA=x5,voSSA=x6
仿真研究
MATLAB Code:
%---------------------------------------
% This is the simulation from
% 两种状态平均法在功率变换器建模的应用比较
%
% hu 2023-03-03
%---------------------------------------clc,clear,close allVin = 20;
R = 10;
L = 1e-3;
C = 1e-6;
f = 40e3;
w = 2 * pi * f;
T = 1 / f;
sim my_power_BuckConverter
D = .5;
q1R = 1 / 2 / pi * sin(2 * pi * D);
q1I = 1 / 2 / pi * (cos(2 * pi * D) - 1);
q0 = D;A = [0 w -1/L 0 0 0-w 0 0 -1/L 0 01/C 0 -1/(R*C) w 0 00 1/C -w -1/(R*C) 0 00 0 0 0 0 -1/L0 0 0 0 1/C -1/(R*C)];
B = [q1R / L, q1I / L, 0, 0, q0 / L, 0]';
x = zeros(6,1);
u = Vin;ts = 0;
h = T/500;
tf = 1e-3;iLGSSAout = [];
voGSSAout = [];
iLSSAout = [];
voSSAout = [];for t=ts:h:tfxdot = A * x + B * u;x = x + xdot * h;iLGSSA = 2 * x(1) * cos(w * t) - 2 * x(2) * sin(w * t) + x(5);voGSSA = 2 * x(3) * cos(w * t) - 2 * x(4) * sin(w * t) + x(6);iLSSA = x(5);voSSA = x(6);iLGSSAout = [iLGSSAout;iLGSSA];voGSSAout = [voGSSAout;voGSSA];iLSSAout = [iLSSAout;iLSSA];voSSAout = [voSSAout;voSSA];
endt = ts:h:tf;
pos = mypos(8);
i = 1;
linewidth = 1.5;
fontsize = 12;
tSIM = iLSIMout.Time;
iLGSSAout_interp = interp1(t,iLGSSAout,tSIM);
iLSSAout_interp = interp1(t,iLSSAout,tSIM);
voGSSAout_interp = interp1(t,voGSSAout,tSIM);
voSSAout_interp = interp1(t,voSSAout,tSIM);figure
plot(tSIM,iLGSSAout_interp,tSIM,iLSSAout_interp,tSIM,iLSIMout.Data,'linewidth',linewidth);
h = legend('$i_{L_{GSSA}}$','$i_{L_{SSA}}$','$i_{L_{SIM}}$');
h.Interpreter = 'latex';
h.FontSize = fontsize;
h.Location = 'southeast';
h.Orientation = 'horizon';
set(gcf,'position',pos{i});
i = i + 1;
grid onfigure
plot(tSIM,voGSSAout_interp,tSIM,voSSAout_interp,tSIM,voSIMout.Data,'linewidth',linewidth);
h = legend('$v_{o_{GSSA}}$', '$v_{o_{SSA}}$', '$v_{o_{SIM}}$');
h.Interpreter = 'latex';
h.FontSize = fontsize;
h.Location = 'southeast';
h.Orientation = 'horizon';
set(gcf,'position',pos{i});
i = i + 1;
grid on
mypos function:
function pos = mypos(i,figs1,figs2)
% mypos.m 给定 figure 对象个数求解合适的摆放位置向量以防止图片堆叠
% i figure 个数
% figs1,figs2 figure 对象的长和高
% pos = mypos(i,figs1,figs2) 求出 i 个 figure 对象的合理摆放位置,且大小设置为[figs1,figs2]
% 输出 pos 是元胞数组,使用规范(已生成figure对象后):set(gcf,'position',pos{i})
% Remark 更方便的绘图程序见 myplot.m% hu 2018-6-11
% hu 2018-8-8 Modified Remark is added
% hu 2018-11-3 Modified Description is updatedif nargin ~= 3figs = [400,300]; %default size is 560*420, 500*280 is suitable for paper shows
elsefigs = [figs1,figs2];
end
if i > 8disp('too many figures! The maximum number is 8')
end
scr = get(0,'screensize');
for k = 1:iif k <= 4pos{k} = [scr(1) + (k - 1) * figs(1),scr(2) + scr(4) / 2,figs];endif k > 4pos{k} = [scr(1) + (k - 5) * scr(3) / 4,scr(2) + 30,figs];end
end
end
真实数据用 SIMULINK 2018a 得到,PWM 频率 f=40kHzf = 40kHzf=40kHz,可以看到 GSSA 基本和 SIMULINK 数据重合,SSA 仅代表了其直流分量


仿真文件: 链接: https://pan.baidu.com/s/1ftQQ68H0nHVZ3LQkPNEObw?pwd=mgf4 提取码: mgf4
相关文章:

广义状态平均法功率变换器建模分析
两种状态平均法在功率变换器建模的应用比较 [!info] Bibliography [1] 高朝晖, 林辉张晓斌 & 吴小华, “两种状态平均法在功率变换器建模的应用比较,” 计算机仿真, no. 241-244248, 2008. [!note] 状态空间平均法采用直流量近似(线性系统模型)&…...

基于Spring Boot的快递管理系统
文章目录 项目介绍主要功能截图:登录我要收件我要寄件个人信息我收到的我寄出的物流管理用户管理部分代码展示设计总结项目获取方式🍅 作者主页:Java韩立 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项…...
)
nerdctl不完全使用指南(开发者)
目录 背景 环境配置 1.编译golang可执行文件 2.快速构建镜像 背景 k8s在1.22版本放弃docker作为runtime后采用了containerd,以containerd作为runtime的k8s安装方法已经出现了很多开源集成工具或者解决方案,在此不做赘述。本篇只要是描述在docker被取…...
)
【独家】华为OD机试 - 分糖果(C 语言解题)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 最近更新的博客使用说明本期…...
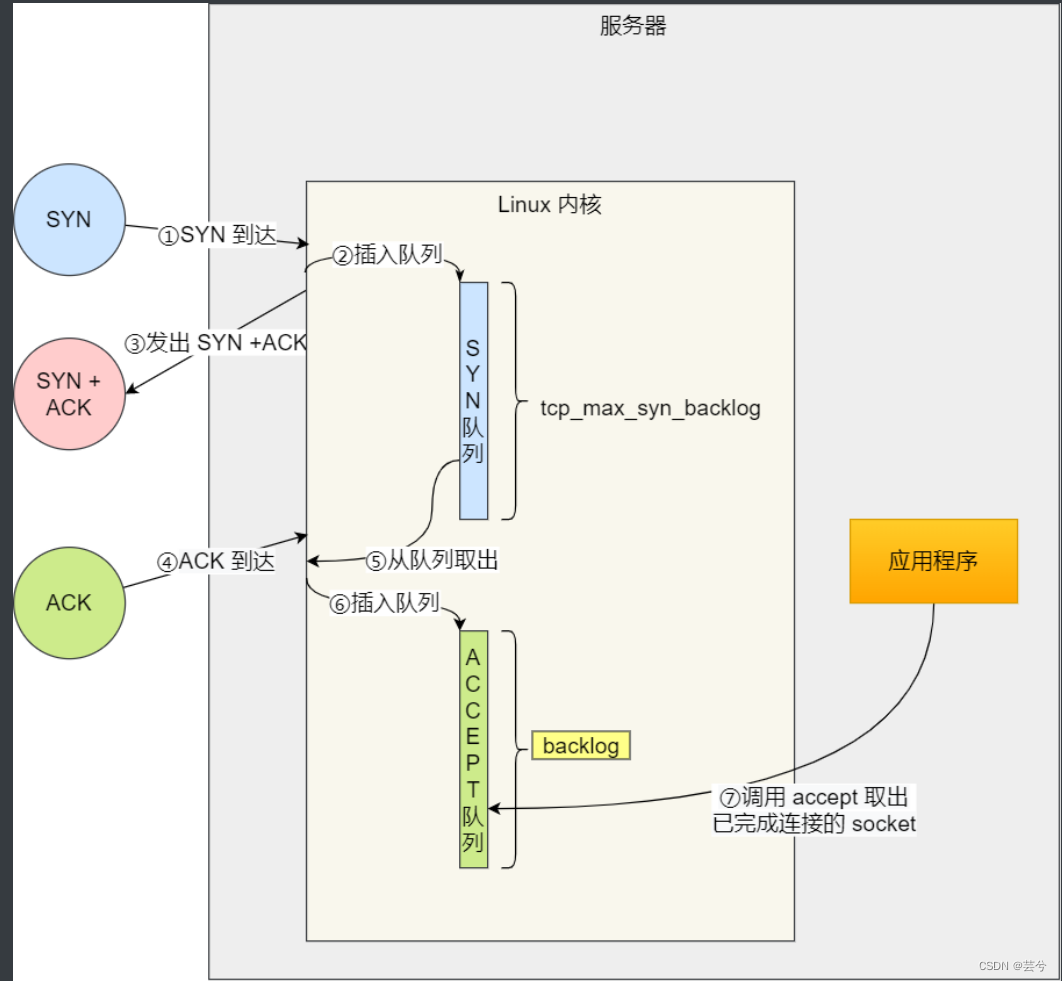
八股总结(二)计算机网络与网络编程
layout: post title: 八股总结(二)计算机网络与网络编程 description: 八股总结(二)计算机网络与网络编程 tag: 八股总结 文章目录计算机网络网络模型网络体系结构在浏览器输入一个网址后回车,背后都发生了什么&#x…...

ChatGPT 一本正经的胡说八道 那也看看原理吧
最近,ChatGPT横空出世。这款被马斯克形容为“强大到危险”的AI,不但能够与人聊天互动,还能写文章、改代码。于是,人们纷纷想让AI替自己做些什么,有人通过两分钟的提问便得到了一篇完美的论文,有人希望它能帮…...

ChatGPT:一个人机环境系统交互的初级产品
从人机环境系统智能的角度看,Chatgpt就是一个还没有开始上道的系统。“一阴一阳之谓道”,Chatgpt的“阴”(默会隐性的部分)尚无体现,就是“阳”(显性描述的部分)还停留在人类与大数据交互的浅层…...
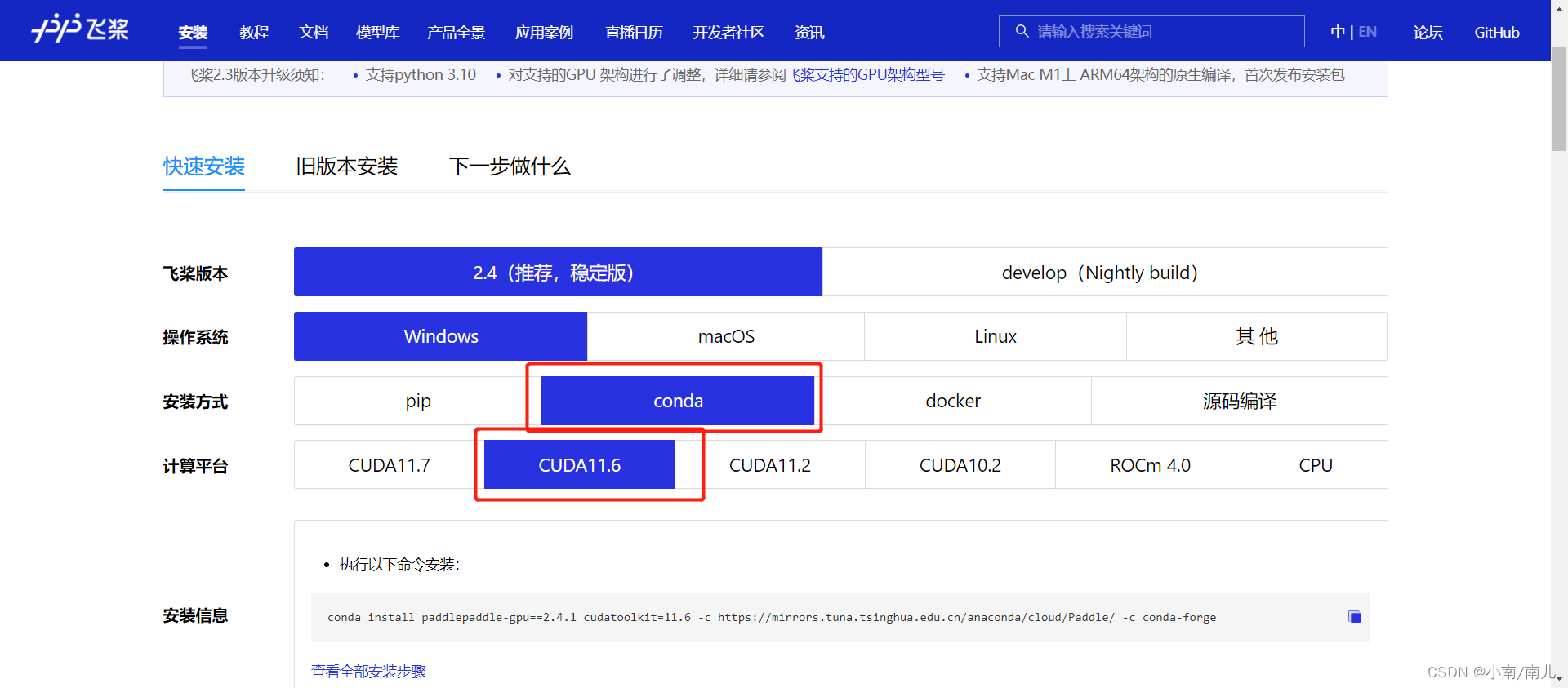
PaddlePaddle本地环境安装(windows11系统)
写在前面: 这里是关于win11安装PaddlePaddle的步骤和方法,建议参考官方的方法。截止2023年3月份,PaddlePaddle的版本是2.4.2。 官方参考:飞桨PaddlePaddle快速安装使用方法 建议使用Anaconda安装 ,关于Anaconda创建环境的可以借鉴:深度学习Anaconda环境搭建(比较全面)…...
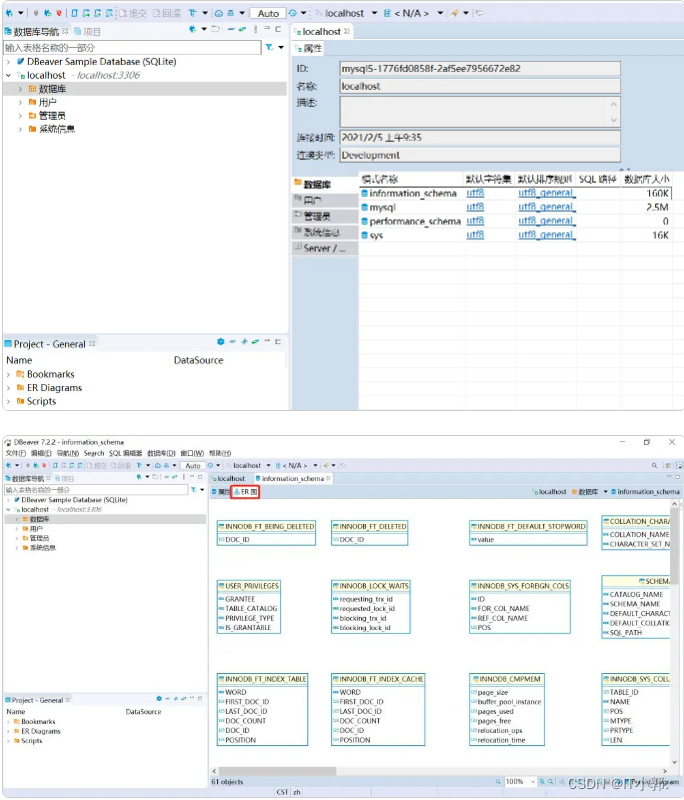
DBeaver 超级详细的安装与使用
一、下载DBeaver DBeaver是一种通用数据库管理工具,适用于需要以专业方式使用数据的每个人;适用于开发人员,数据库管理员,分析师和所有需要使用数据库的人员的免费(DBeaver Community) 的多平台数据库工具。 DBeaver支持80多个数据…...

计算机网络的166个概念 你知道几个第七部分
计算机网络传输层 可靠数据传输:确保数据能够从程序的一端准确无误的传递给应用程序的另一端。 容忍丢失的应用:应用程序在发送数据的过程中可能会存在数据丢失的情况。 非持续连接:每个请求/响应会对经过不同的连接,每一个连接…...

海尔三翼鸟:生态聚拢的密度,决定场景落地速度
最近学到一个新词,叫做涌现能力。 怎么理解呢?我们以当下最火的ChatGPT为例,GPT1模型是1.17亿参数,GPT2有15亿参数,GPT3有1750亿个参数。研究人员在放大模型规模的进程中发现一个惊人的现象,模型参数达到一…...

前端基础知识
文章目录前端基础知识HTML1. html基本结构2.常见的html标签注释标签标题标签(h1~h6)段落标签p换行标签 br格式化标签图片标签:img超链接标签表格标签列表标签表单标签input标签label标签select标签textarea 标签盒子标签div&span3. html特殊字符CSS1. 基本语法2…...

LiveData 面试题库、解答、源码分析
引子LiveData 是能感知生命周期的,可观察的,粘性的,数据持有者。LiveData 用于以“数据驱动”方式更新界面。换一种描述方式:LiveData 缓存了最新的数据并将其传递给正活跃的组件。关于数据驱动的详解可以点击我是怎么把业务代码越…...

kotlin用object实现单例模式,companion object与java静态
kotlin用object实现单例模式,companion object与java静态 kotlin中很容易使用object实现java中的单例模式。由于kotlin中没有static修饰词,可以用companion object实现Java中的static效果。 //object相当于java的单例 object Singleton {var count: In…...

智慧楼宇中的“黑科技”
据不完全统计,无论是居家、办公、学习还是社交,人们有80%的时间都是在室内空间度过的。而随着社会生产力水平与人们消费理念的提升,用户对于楼宇建筑的使用要求也在不断提高,从最基本的舒适为先逐步朝着数字化、智慧化升级。 如果…...

炫云渲染质量功能测试
炫云已经支持优化渲染质量,分别是保守优化、中度优化和深度优化,使用后效果图的渲染时间会有所缩短,尤其对低版本V-Ray和参数设置不当的场景非常有效,能大幅提升渲染速度及节省渲染费用,当然最终效果图有可能有稍许差异…...

SpringBoot入门
文章目录前言一、约定大于配置二、使用步骤1.使用IDEA创建SpringBoot项目2.引入依赖3.测试三、application.properties和application.yml配置文件四、application.yml配置多环境五、测试:总结前言 SpringBoot并不是一门新的技术栈,它的主要目的是为了去…...
)
D. Constant Palindrome Sum(差分数组维护)
Problem - D - Codeforces 题意:给定长度为n的数组,每次操作可以选择一个数令a[i]变成[1,k]范围内的一个数,问最少需要多少次操作可以让a[i]a[n-i1]x (1< i < n/2)满足。 思路:利用差分数组d[i]表示x取i需要的总操作数。 …...
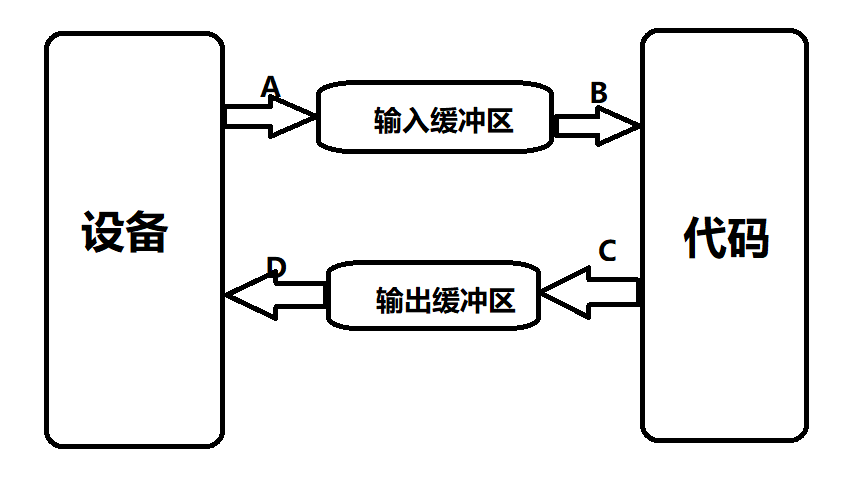
【C++】30h速成C++从入门到精通(IO流)
C语言的输入与输出C语言中我们用到的最频繁的输入输出方式就是scanf ()与printf()。 scanf(): 从标准输入设备(键盘)读取数据,并将值存放在变量中。printf(): 将指定的文字/字符串输出到标准输出设备(屏幕)。注意宽度输出和精度输出控制。C语言借助了相应的缓冲区来…...
文件变成chk如何恢复正常
许多人不知道chk文件是什么?其实它是用户在使用“磁盘碎片整理程序”整理硬盘后所产生的“丢失簇的恢复文件”,而在u盘、内存卡等移动设备读取数据过程中,由于断电或强制拔出也容易产生大量的chk文件。那么文件变成chk如何恢复正常呢…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...

欢乐熊大话蓝牙知识17:多连接 BLE 怎么设计服务不会乱?分层思维来救场!
多连接 BLE 怎么设计服务不会乱?分层思维来救场! 作者按: 你是不是也遇到过 BLE 多连接时,调试现场像网吧“掉线风暴”? 温度传感器连上了,心率带丢了;一边 OTA 更新,一边通知卡壳。…...
