算法练习:前缀和
目录
- 1. 一维前缀和
- 2. 二维前缀和
- 3. 寻找数组中心下标
- 4. 除自身以外数组的乘积
- 5. !和为k的子数字
- 6. !和可被k整除的子数组
- 7. !连续数组
- @8. 矩阵区域和
1. 一维前缀和
- 题目信息:
- 题目链接:
一维前缀和- 思路:求前缀和数组,sum = dp[r] - dp[l - 1]
#include <iostream>
#include <vector>
using namespace std;int main()
{int n = 0;int q = 0;cin >> n >> q;//先求前缀和数组int num = 0;//计算时可能溢出vector<long long> dp;dp.push_back(0);for(int i = 0; i < n; i++){cin >> num;dp.push_back(num + dp[i]);}//求询问区间之和//dp[i] - dp[i - 1]//计算时可能溢出vector<long long> ret;int left = 0,right = 0;for(int i = 0; i < q; i++){cin >> left >> right;ret.push_back(dp[right] - dp[left - 1]);}for(auto e : ret){cout << e << endl;}return 0;
}
优化:
int main()
{int n = 0;int q = 0;cin >> n >> q;//先求前缀和数组int num = 0;//默认初始化为0vector<int> arr(n + 1);for(int i = 1; i < n + 1; i++){cin >> num;arr[i] = num;}//防溢出vector<long long> dp(n + 1);for(int i = 1; i < n + 1; i++){dp[i] = dp[i - 1] + arr[i];}int l = 0, r = 0;while(q--){cin >> l >> r;cout << dp[r] - dp[l - 1] << endl;}return 0;
}
2. 二维前缀和
- 题目信息:
- 题目链接:
二维前缀和- 思路:二维前缀和
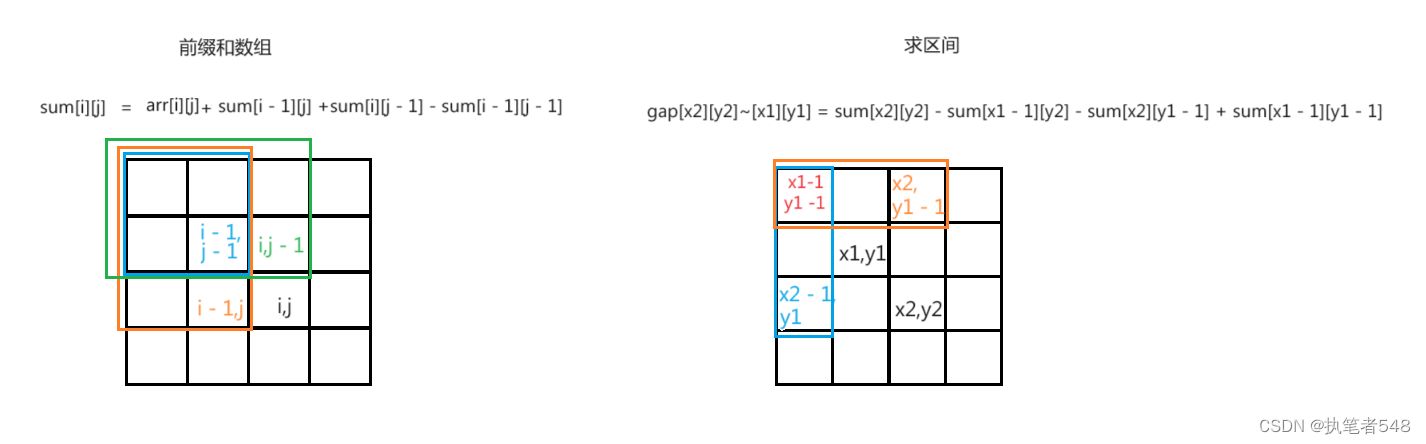
int main()
{int n = 0, m = 0, q = 0;//先遍历,得值 cin >> n >> m >> q;vector<vector<long long>> arr;vector<long long> part(m + 1);for (int i = 0; i < n + 1; i++){arr.push_back(part);}vector<vector<long long>> dp(arr);for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){cin >> arr[i][j];}}//求前缀和数组for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){dp[i][j] = arr[i][j] + dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1];}}//求区间值//x1,y1小,x2,y2大int x1, x2, y1, y2 = 0;while (q--){cin >> x1 >> y1 >> x2 >> y2;cout << dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1] << endl;}return 0;
}
3. 寻找数组中心下标
- 题目信息:
- 题目链接:
寻找数组的中心下标- 思路:正向与逆向前缀和数组,边界处理,特殊情况处理
class Solution
{
public:int pivotIndex(vector<int>& nums){int n = nums.size();vector<int> dp1(n);vector<int> dp2(n);//空if(nums.size() == 1){return 0;}int left = 0, right = nums.size() - 1;//求前缀和数组//顺序while (left < nums.size()){if (left > 0){dp1[left] = nums[left] + dp1[left - 1];}else{dp1[left] = nums[left];}left++;}//倒序while (right >= 0){if (right < nums.size() - 1){dp2[right] = nums[right] + dp2[right + 1];}else{dp2[right] = nums[right];}right--;}//遍历求中间结点for (int cur = 0; cur < nums.size(); cur++){//dp1顺序//dp2倒序if (cur == 0){if (dp2[cur + 1] == 0){return cur;}}else if (cur == nums.size() - 1){if (dp1[cur - 1] == 0){return cur;}}else{if (dp1[cur - 1] == dp2[cur + 1]){return cur;}}}return -1;}
};
优化:
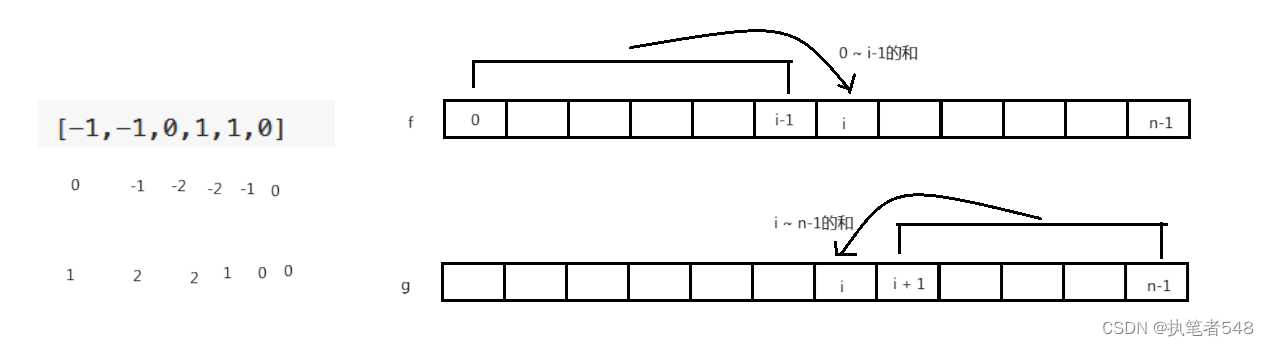
class Solution
{
public:int pivotIndex(vector<int>& nums) {int n = nums.size();//顺序vector<int> f(n);//逆序vector<int> g(n);//边界问题特殊处理f[0] = 0;//f[i] -> [0, i - 1]for(int i = 1; i < n; i++){f[i] = nums[i - 1] + f[i - 1];}g[n - 1] = 0;for(int i = n - 2; i >= 0; i--){g[i] = g[i + 1] + nums[i + 1];}for(int i = 0; i < n; i++){if(f[i] == g[i]){return i;}}return -1;}
};
4. 除自身以外数组的乘积
- 题目信息:
- 题目链接:
除自身以外数组的乘积- 思路:前缀 + 后缀数组
class Solution
{
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> f(n);vector<int> g(n);f[0] = nums[0];for(int i = 1; i < n; i++){f[i] = nums[i] * f[i - 1];}g[n - 1] = nums[n - 1];for(int i = n - 2; i >= 0; i--){g[i] = nums[i] * g[i + 1];}vector<int> ret(n);for(int i = 0; i < n; i++){if(i == 0){ret[i] = g[i + 1];}else if(i == n - 1){ret[i] = f[i - 1];}else{ret[i] = g[i + 1] * f[i - 1];}}return ret;}
};
优化:
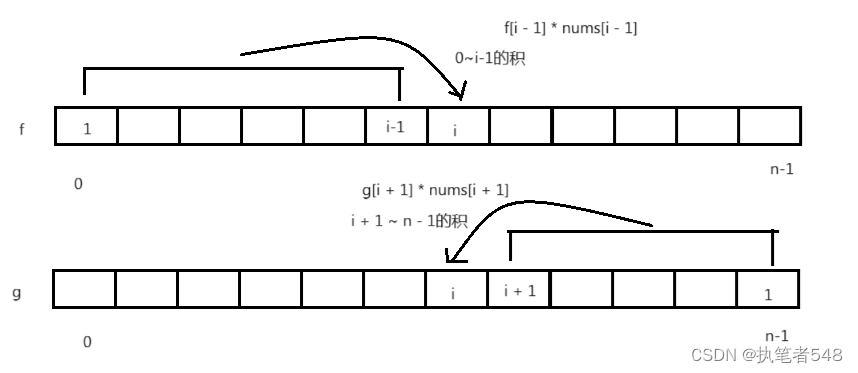
class Solution
{
public:vector<int> productExceptSelf(vector<int>& nums) {int n = nums.size();vector<int> f(n);vector<int> g(n);f[0] = 1;//顺序for(int i = 1; i < n; i++){f[i] = f[i - 1] * nums[i - 1];}g[n - 1] = 1;//逆序for(int i = n - 2; i >= 0; i--){g[i] = g[i + 1] * nums[i + 1];}vector<int> ret(n);for(int i = 0; i < n; i++){ret[i] = f[i] * g[i];}return ret;}
};
5. !和为k的子数字
- 题目信息:
- 题目链接:
和为k的子数组- 思路:前缀和,元素没有单调性,无法使用滑动窗口,逆向求sum - k,可以求得为i为尾的所有数组
class Solution
{
public:int subarraySum(vector<int>& nums, int k) {int ret = 0;unordered_map<int ,int> hash;//sum - k == 0时,即sum就为khash[0] = 1;int sum = 0;//用哈希表代替遍历for(auto e : nums){sum += e;if(hash.count(sum - k)){ret += hash[sum - k];}//插入哈希表//可能存在重复前缀和hash[sum]++;}return ret;}
};
6. !和可被k整除的子数组
- 题目信息:
- 题目链接:
和可被k整除的子数组- 思路:前缀和,哈希表,同余定理,C++中负数除以整数的余数修正(num % k + k) % k
class Solution
{
public:int subarraysDivByK(vector<int>& nums, int k) {int sum = 0;unordered_map<int,int> hash;int ret = 0;int count = 0;//sum % k 本身就符合要求hash[0] = 1;for(auto e : nums){sum += e;//(sum1 - sum2) % k == 0//同余定理//负数除整数的余数//哈希表中存余数if(hash.count((sum % k + k) % k)){ret += hash[(sum % k + k) % k];}hash[(sum % k + k) % k]++;}return ret;}
};
7. !连续数组
- 题目信息:
- 题目链接:
连续数组
3.思路:前缀加哈希表,求长度,记录下标
class Solution
{
public:int findMaxLength(vector<int>& nums) {for(auto& e : nums){if(e == 0){e = -1;}}unordered_map<int,int> hash;int sum = 0;int len = 0;//细节,刚好sum为0hash[0] = -1;for(int i = 0; i < nums.size(); i++){//将所有的前缀和与对应下标记录至哈希表中sum += nums[i];//返回的是长度,最长数组的长度if(hash.count(sum) && len < i - hash[sum]){len = i - hash[sum];}//不存在添加下标if(!hash.count(sum)){hash[sum] = i;}}return len;}
};
@8. 矩阵区域和
- 题目信息:
- 题目链接:
矩阵区域和- 思路:前缀和二维数组,边界问题分析
思路:
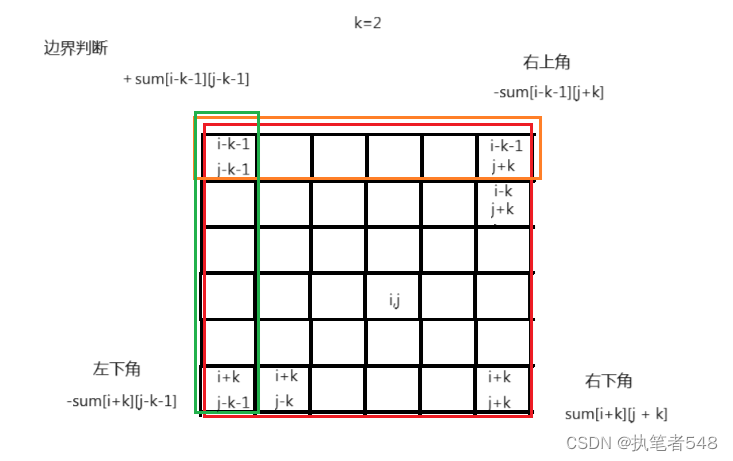
边界问题:
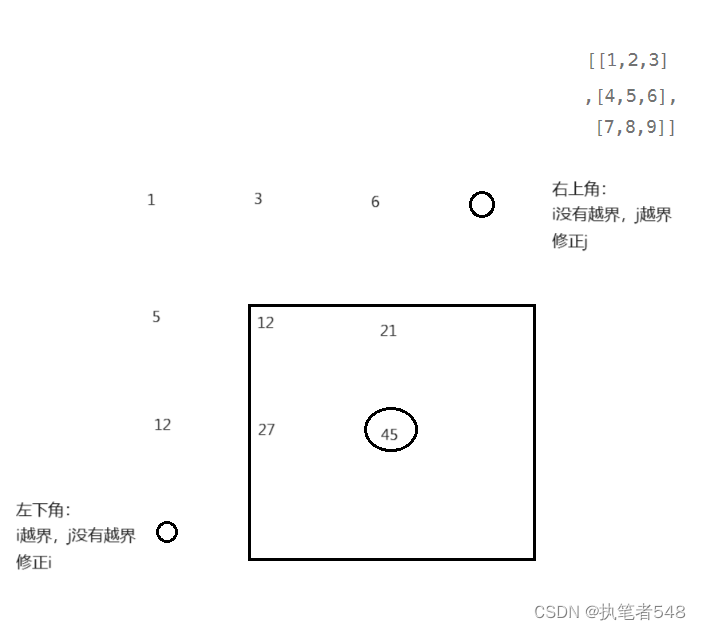
class Solution
{
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k){vector<int> part1(mat[0].size(), 0);vector<vector<int>> answer(mat.size(), part1);vector<int> part2(mat[0].size() + 1, 0);vector<vector<int>> dp(mat.size() + 1, part2);//二维数组的前缀和for (int i = 1; i < dp.size(); i++){for (int j = 1; j < dp[0].size(); j++){dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];}}for (int i = 0; i < mat.size(); i++){for (int j = 0; j < mat[0].size(); j++){int sum = 0;//右下角//边界情况,修正int pos1 = i + k + 1;int pos2 = j + k + 1;if (pos1 >= dp.size()){pos1 = dp.size() - 1;}if (pos2 >= dp[0].size()){pos2 = dp[0].size() - 1;}sum += dp[pos1][pos2];//右上角pos1 = i - k;pos2 = j + k + 1;//i符合,j不符合if (pos1 >= 1 && pos2 >= dp[0].size()){pos2 = dp[0].size() - 1;}if (pos1 >= 1 && pos2 < dp[0].size()){sum -= dp[pos1][pos2];}//左下角pos1 = i + k + 1;pos2 = j - k;//i不符合,j符合if (pos1 >= dp.size() && pos2 >= 1){pos1 = dp.size() - 1;}if (pos1 < dp.size() && pos2 >= 1){sum -= dp[pos1][pos2];}//左上角if (i - k >= 1 && j - k >= 1){sum += dp[i - k][j - k];}answer[i][j] = sum;}}return answer;}
};
相关文章:

算法练习:前缀和
目录 1. 一维前缀和2. 二维前缀和3. 寻找数组中心下标4. 除自身以外数组的乘积5. !和为k的子数字6. !和可被k整除的子数组7. !连续数组8. 矩阵区域和 1. 一维前缀和 题目信息: 题目链接: 一维前缀和思路:求前缀和数组,sum dp[r] …...

Kafka MQ 生产者
Kafka MQ 生产者 生产者概览 尽管生产者 API 使用起来很简单,但消息的发送过程还是有点复杂的。图 3-1 展示了向 Kafka 发送消息的主要步骤。 我们从创建一个 ProducerRecord 对象开始,ProducerRecord 对象需要包含目标主题和要发送的内容。我们还可以…...

SQLiteC/C++接口详细介绍之sqlite3类(十)
返回目录:SQLite—免费开源数据库系列文章目录 上一篇:SQLiteC/C接口详细介绍之sqlite3类(九) 下一篇:SQLiteC/C接口详细介绍之sqlite3类(十一) 30.sqlite3_enable_load_extension&#x…...

Vue中nextTick一文详解
什么是 nextTick? 在 Vue 中,当我们修改数据时,Vue 会自动更新视图。但是,由于 JavaScript 的事件循环机制,我们无法立即得知视图更新完成的时机。这时候,我们就需要使用 nextTick 来获取视图更新完成后的…...

爱奇艺 CTR 场景下的 GPU 推理性能优化
01 背景介绍 GPU 目前大量应用在了爱奇艺深度学习平台上。GPU 拥有成百上千个处理核心,能够并行的执行大量指令,非常适合用来做深度学习相关的计算。在 CV(计算机视觉),NLP(自然语言处理)的模型…...
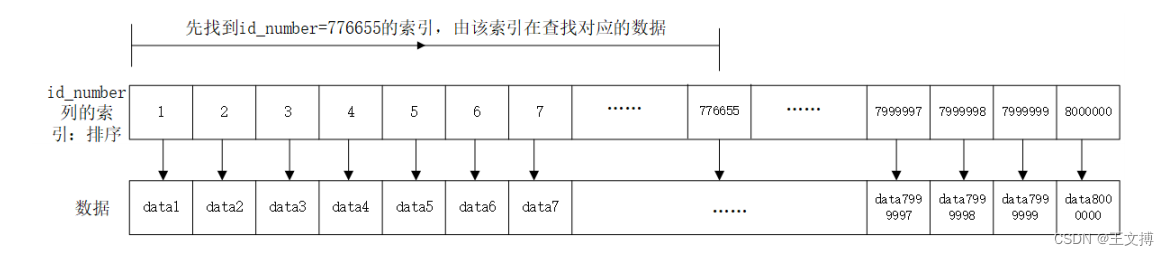
详解MySql索引
目录 一 、概念 二、使用场景 三、索引使用 四、索引存在问题 五、命中索引问题 六、索引执行原理 一 、概念 索引是一种特殊的文件,包含着对数据表里所有记录的引用指针。暂时可以理解成C语言的指针,文章后面详解 二、使用场景 数据量较大,且…...

struct 和 union 的区别?
struct和union的分对应点总结 存储方式: struct:struct中的每个成员都拥有独立的内存空间。一个struct变量的总长度是其所有成员的长度之和,且通常会根据编译器的内存对齐规则进行适当调整。union:union中的所有成员共享同一段内…...
Linux - 安装 Jenkins(详细教程)
目录 前言一、简介二、安装前准备三、下载与安装四、配置镜像地址五、启动与关闭六、常用插件的安装 前言 虽然说网上有很多关于 Jenkins 安装的教程,但是大部分都不够详细,或者是需要搭配 docker 或者 k8s 等进行安装,对于新手小白而已&…...

【JAVA】JAVA方法的学习和创造
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法|MySQL| 💫个人格言:“没有罗马,那就自己创造罗马~” 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不…...
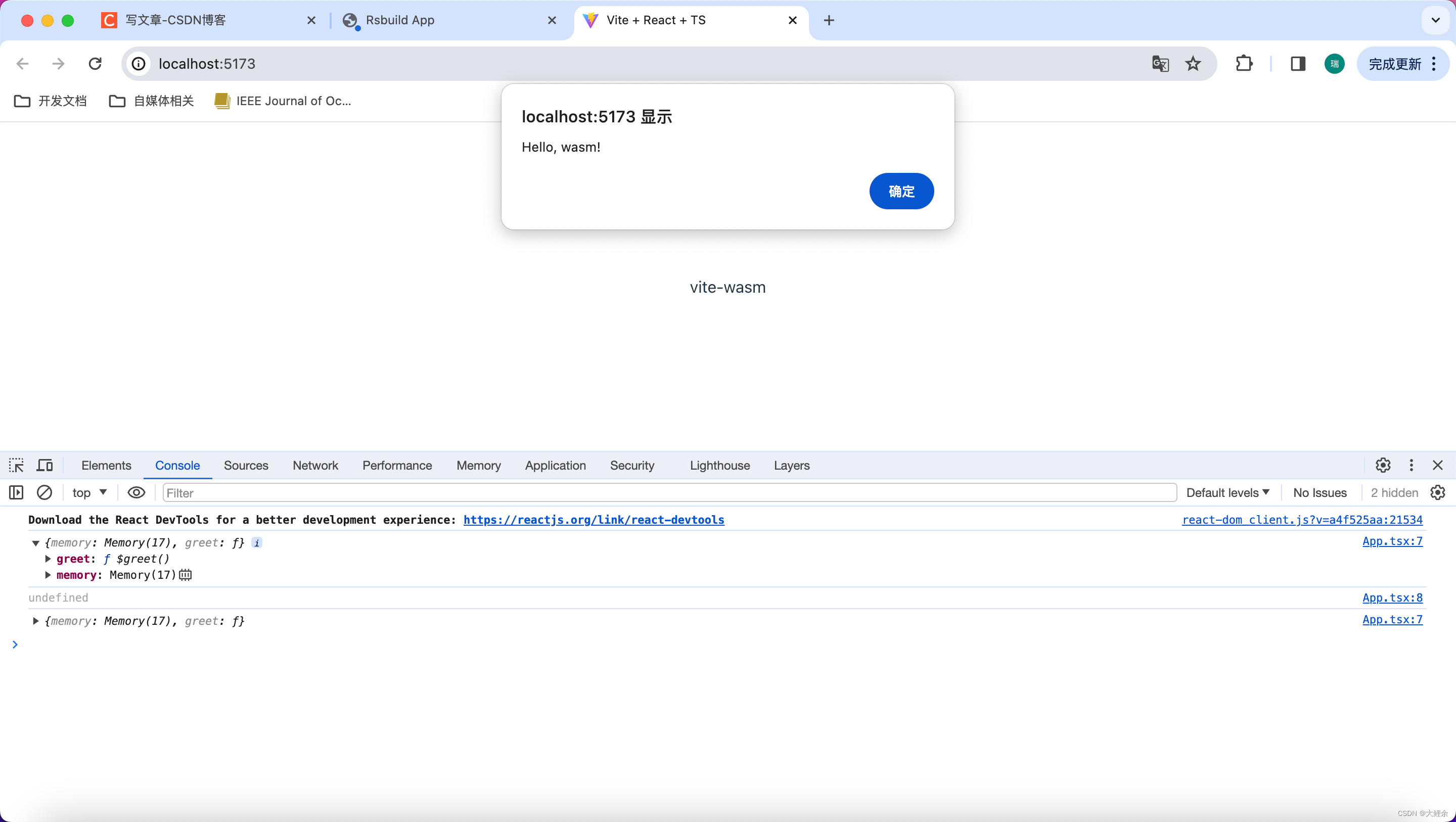
Rust写一个wasm入门并在rspack和vite项目中使用(一)
rust打包wasm文档 文档地址 安装cargo-generate cargo install cargo-generate 安装过程中有问题的话手动安装cargo-generate下载地址 根据自己的系统下载压缩包,然后解压到用户/.cargo/bind目录下,将解压后的文件放到该目录下即可。 创建wasm项目 …...

HTTP和HTTPS的区别,HTTPS加密原理是?
HTTP和HTTPS都是网络传输协议,主要用于浏览器和服务器之间的数据传输,但它们在数据传输的安全性、加密方式、端口等方面有所不同。 数据传输的安全性:HTTP是明文传输,数据不加密,容易被黑客窃听、篡改或者伪造&#x…...

基于Spring Boot+Vue的校园二手交易平台
目录 一、 绪论1.1 开发背景1.2 系统开发平台1.3 系统开发环境 二、需求分析2.1 问题分析2.2 系统可行性分析2.2.1 技术可行性2.2.2 操作可行性 2.3 系统需求分析2.3.1 学生功能需求2.3.2 管理员功能需求2.3.3游客功能需求 三、系统设计3.1 功能结构图3.2 E-R模型3.3 数据库设计…...

什么是软件开发?软件开发阶段划分是什么?并以LabVIEW为例进行说明
软件开发是一种创建、设计、编码、测试和维护应用程序、框架或其他软件组件的过程。它涉及从理解需求到设计、实现、测试、部署和最终维护的全过程。软件开发可以用来创建新的软件应用、系统软件、游戏、或开发网络应用等。 软件开发过程通常可以分为以下几个阶段:…...

PTAL1-006 连续因子
c语言中的小小白-CSDN博客c语言中的小小白关注算法,c,c语言,贪心算法,链表,mysql,动态规划,后端,线性回归,数据结构,排序算法领域.https://blog.csdn.net/bhbcdxb123?spm1001.2014.3001.5343 给大家分享一句我很喜欢我话: 知不足而奋进,望远山而前行&am…...
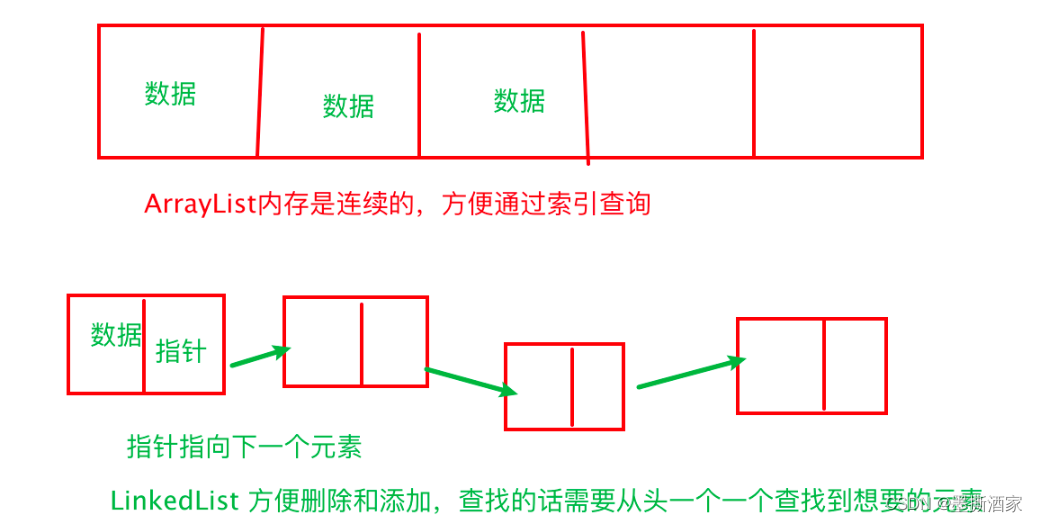
【Java】容器|Set、List、Map及常用API
目录 一、概述 二、List 1、List的常用API 2、ArrayList 3、List遍历 三、Set 1、Set的常用方法: 2、HashSet 3、遍历集合: 四、Map 1、Map常用API 2、HashMap 3、遍历Map 五、迭代器 一、概述 在Java中所有的容器都属于Collection接口下的内容 1…...
Navicat 面试题及答案整理,最新面试题
Navicat 在数据库管理中的主要用途有哪些? Navicat 是一款数据库管理工具,其主要用途包括: 1、多数据库支持: Navicat 支持多种数据库连接,包括 MySQL、Oracle、PostgreSQL、SQLite、SQL Server 等,方便用…...

android studio 连接mumu模拟器调试
1、打开mumu模拟器 2、在Android Studio 中 控制台 cd 到 sdk 目录下 platform-tools 文件夹,有一个adb.exe 可运行程序 一般指令: adb connect 127.0.0.1:7555 但是这个执行在window环境下可能会报错 解决方法是在 adb 之前加 ".\", 问题…...

四连通与八连通的区别 -- 图例讲解
概念 四连通区域:指从某个点出发,只能通过上、下、左、右四个方向的运动到达区域内的其他点,且不能跨越区域的边界。 八连通区域:除了上、下、左、右四个方向,还可以沿对角线方向(左上、右上、左下、右下…...
关于分布式微服务数据源加密配置以及取巧方案(含自定义加密配置)
文章目录 前言Spring Cloud 第一代1、创建config server项目并加入加解密key2、启动项目,进行数据加密3、实际项目中的测试server Spring Cloud Alibaba低版本架构不支持,取巧实现无加密配置,联调环境问题加密数据源配置原理探究自定义加密解…...
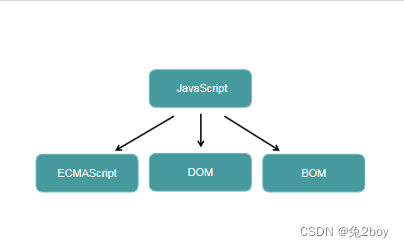
快速了解JavaScript
1.1 javaScript 历史 创始人 布兰登 艾奇 生于1961年 在1995设计LiveScript后改名为JavaScript 1.2 javaScript 是什么类型的语言 JavaScript是一种在客户端运行的脚本语言(不需要编译,由js引擎逐行解释执行) 1.3 JavaScript可以做什么 …...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...








