设计模式在芯片验证中的应用——装饰器
一、装饰器模式
装饰器模式(Decorator)是一种结构化软件设计模式,它提供了一种通过向类对象添加行为来修改类对象的方法,而不会影响同一类的其它对象行为。该模式允许在不修改抽象类的情况下添加类功能。它从本质上允许基类代码对不可预见的修改具有前瞻性。
对于经常需要在最后时刻新增特性的验证工作,装饰器模式的这个特性非常强大。该模式适用于通过向复杂数据项应用额外的约束集来对它们进行建模,或者在原先数据上添加额外数据。与类继承相比,它的主要优点是可以实现向类对象中动态添加或删减行为。在工程中,该技术被广泛用于实现受约束随机激励的生成。
举个例子,如下图,我们在验证环境中打算开发一个Arm指令生成器,原先RTL只支持基本的load和store指令,过段时间可能又支持atomic指令,再过段时间可能又支持SVE指令了,这样就容易造成我们需要对以往的代码不停地修改。更令人崩溃的是,RTL又搞了其它版本,有的版本只支持load/store指令和SVE指令,有的版本只支持atomic和SVE指令,等等。对于这些行为,第一个跳入脑海的想法可能就是扩展它所属的类,在新的类中添加新功能,但这种方式会使代码量迅速膨胀,而且可能会破坏之前写好的代码。
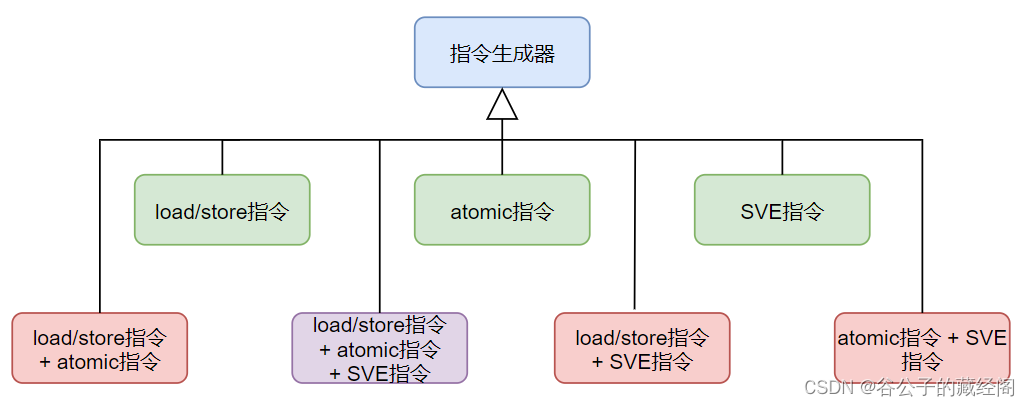
针对以上情况,我们可以考虑使用装饰器模式。要构建装饰器设计模式,需要定义几个主要部分:
- 被包装对象:它声明了被包装对象的共用接口和基本行为,装饰器会在此基础上添加新的行为。
- 抽象装饰器:定义了基本的装饰器,它拥有一个指向被被包装对象的引用成员变量,因此会将操作委派给被包装的对象。
- 具体装饰器:定义了可动态增减到被包装对象的额外行为。具体装饰器会重写装饰基类的方法,并在调用父类方法之前或之后进行额外的行为。
下图使用UML类图提供了上述三者之间的图形化关系:
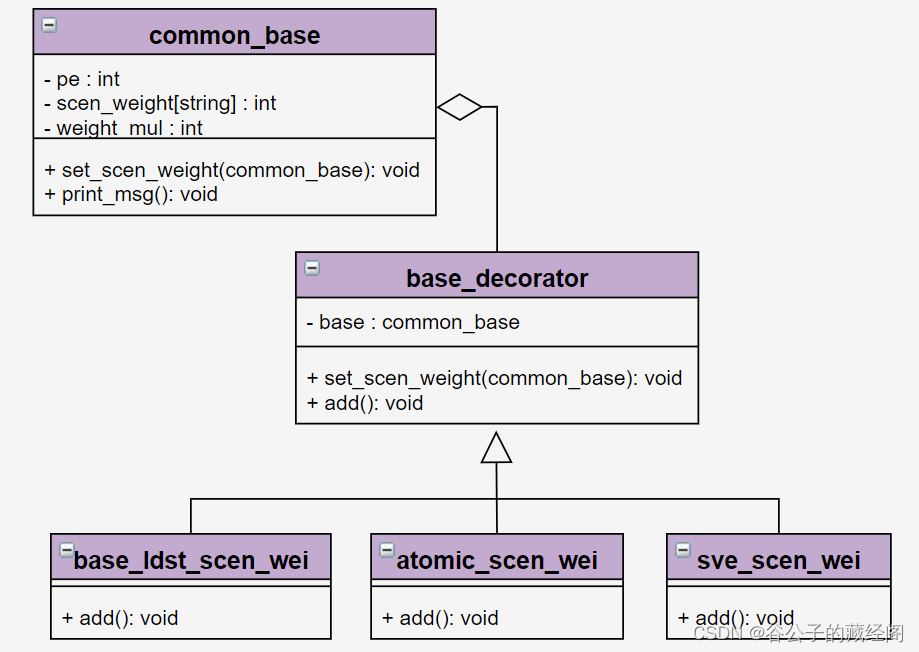
装饰器设计模式背后的主要思想是,各种具体装饰器可以在仿真过程中处于活动状态,灵活地为被包装对象增加新功能。而且可以指令任意组合的具体装饰器同时处于活动状态,这样就可以在任意给定时刻,向被包装的对象添加任何期望的激励组合。
二、参考代码
指令生成器的装饰器模式参考代码如下:
class common_base;int pe;int scen_weight[string];int weight_mul = 1;virtual function void set_scen_weight(common_base _h);endfunction : set_scen_weightvirtual function void print_msg();foreach ( scen_weight[t_scen] ) begin$display("scen[%s]=%0d is added", t_scen, scen_weight[t_scen]);endendfunction : print_msgendclass : common_baseclass base_decorator extends common_base;common_base base;virtual function void set_scen_weight(common_base _h);add();base = _h;foreach ( scen_weight[t_scen] ) beginif ( base.scen_weight.exists(t_scen) ) begin`uvm_error("decorator", $psprintf("The scen(%s) has exists", t_scen))end else beginbase.scen_weight[t_scen] = scen_weight[t_scen] * weight_mul;endendprint_msg();endfunction : set_scen_weightvirtual function void add();endfunction : addendclass : base_decoratorclass base_ldst_scen_wei extends base_decorator;virtual function void add();scen_weight["load"] = 10;scen_weight["store"] = 10;endfunction : addendclass : base_ldst_scen_weiclass atomic_scen_wei extends base_decorator;virtual function void add();scen_weight["atomic_add"] = 5;scen_weight["atomic_sub"] = 5;endfunction : addendclass : atomic_scen_weiclass sve_scen_wei extends base_decorator;virtual function void add();scen_weight["gather"] = 8;scen_weight["scatter"] = 8;endfunction : addendclass : sve_scen_wei模拟测试代码如下:
class scen_weight_gen;rand bit base_ldst_scen;rand bit atomic_scen;rand bit sve_scen;function void gen();common_base base = new();common_base common;`uvm_info("", $psprintf("base_ldst_scen:%b, atomic_scen:%b, sve_scen:%b", base_ldst_scen, atomic_scen, sve_scen), UVM_LOW)if ( base_ldst_scen ) begincommon = base_ldst_scen_wei::new();common.set_scen_weight(base);endif ( atomic_scen ) begincommon = atomic_scen_wei::new();common.weight_mul = 3;common.set_scen_weight(base);endif ( sve_scen ) begincommon = sve_scen_wei::new();common.set_scen_weight(base);endendfunction : genendclass : scen_weight_gen输出仿真日志如下:
base_ldst_scen:1, atomic_scen:1, sve_scen:0| # scen[load]=10 is added| # scen[store]=10 is added| # scen[atomic_add]=5 is added| # scen[atomic_sub]=5 is added从仿真结果可以看出,scen_weight_gen类随机后,base_ldst_scen为1,atomic_scen为1,sve_scen为0,因此只有load/store指令和atomic指令功能被添加到指令生成器中。
好了,今天就写到这里了。下次给大家分享下设计模式中策略模式(Strategy)在芯片验证中的应用。它和装饰器模式很类似,区别是装饰器模式可让你更改对象的外表,但策略模式则让你能够更改其本质。

相关文章:

设计模式在芯片验证中的应用——装饰器
一、装饰器模式 装饰器模式(Decorator)是一种结构化软件设计模式,它提供了一种通过向类对象添加行为来修改类对象的方法,而不会影响同一类的其它对象行为。该模式允许在不修改抽象类的情况下添加类功能。它从本质上允许基类代码对不可预见的修改具有前瞻…...

Python 查找并高亮PDF中的指定文本
在处理大量PDF文档时,有时我们需要快速找到特定的文本信息。本文将提供以下三个Python示例来帮助你在PDF文件中快速查找并高亮指定的文本。 查找并高亮PDF中所有的指定文本查找并高亮PDF某个区域内的指定文本使用正则表达式搜索指定文本并高亮 本文将用到国产第三方…...

LEETCODE LCS 03. 主题空间
题目描述如上,这个题主要运用了DFS的思想,同时走过的路径标记为6,即可在后续的遍历中过滤掉重复的元素,其他则类似边界条件的判断和题目条件的判断,求最大值,只需要一次遍历中累加对比每一次得即可。 模板&…...
【Spring Boot 源码学习】深入应用上下文初始化器实现
《Spring Boot 源码学习系列》 深入应用上下文初始化器实现 一、引言二、往期内容三、主要内容3.1 spring-boot 子模块中内置的实现类3.1.1 ConfigurationWarningsApplicationContextInitializer3.1.2 ContextIdApplicationContextInitializer3.1.3 DelegatingApplicationConte…...
【Docker】一文趣谈Docker
🏡浩泽学编程:个人主页 🔥 推荐专栏:《深入浅出SpringBoot》《java对AI的调用开发》 《RabbitMQ》《Spring》《SpringMVC》《项目实战》 🛸学无止境,不骄不躁,知行合一 文章目录 …...
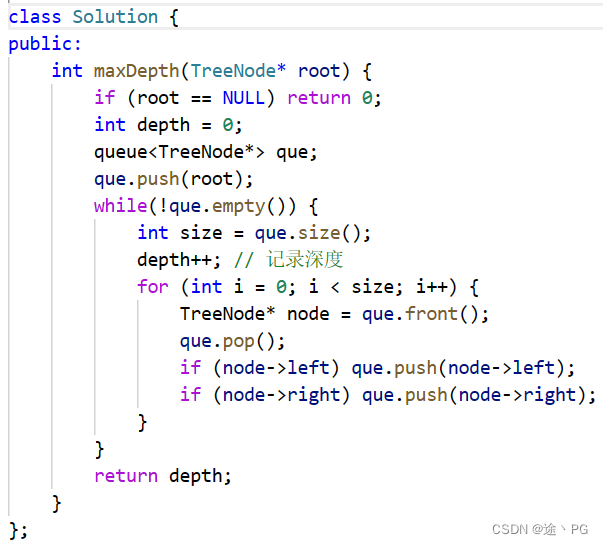
代码随想录day19(2)二叉树:二叉树的最大深度(leetcode104)
题目要求:求出二叉树的最大深度 思路:首先要区分二叉树的高度与深度。二叉树的高度是任一结点到叶子结点的距离,而二叉树的深度指的是任一节点到根节点的距离(从1开始)。所以求高度使用后序遍历(从下往上&…...
)
Lua中文语言编程源码-第五节,更改lcorolib.c协程库函数, 使Lua加载中文库关键词(与所有的基础库相关)
源码已经更新在CSDN的码库里: git clone https://gitcode.com/funsion/CLua.git 在src文件夹下的lcorolib.c协程库函数,Coroutine Library:表明这个C源文件实现了Lua的协程库(Coroutine Library),即提供了…...
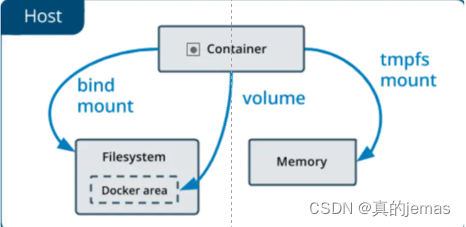
Docker学习之数据管理(超详解析)
Docker存储资源类型: 用户在使用 Docker 的过程中,势必需要查看容器内应用产生的数据,或者需要将容器内数据进行备份,甚至多个容器之间进行数据共享,这必然会涉及到容器的数据管理: (1ÿ…...

FDTD液晶折射率各项异性表示方法
由于FDTD的数据都是沿坐标轴的,各向异性材料的参数也需要根据坐标轴来输入。 首先要了解坐标变换。 坐标变换 这里以二维坐标变化为例。 矢量下我们可以发现OP可在两个坐标系下分别表示 接下来将两个坐标相互关联,这里以Xb举例,Yb同理 注…...
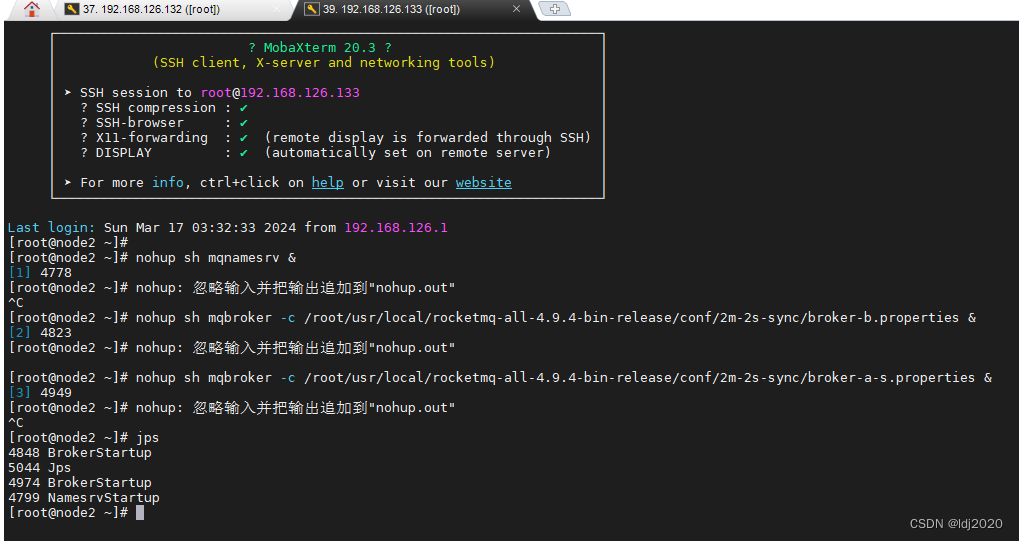
RoketMQ主从搭建
vim /etc/hosts# IP与域名映射,端口看自己的#nameserver 192.168.126.132 rocketmq-nameserver1 192.168.126.133 rocketmq-nameserver2# 注意主从节点不在同一个主机上 #broker 192.168.126.132 rocketmq-master1 192.168.126.133 rocketmq-master2#broker 192.168…...
)
Linux网络瑞士军刀 nc(netcat)
1.命令简介 nc(netcat)是一个短小精悍、功能实用、简单可靠的网络工具,主要有如下作用: (1)端口侦听,nc 可以作为 server 以 TCP 或 UDP 方式侦听指定端口; (2&#x…...
1.Spring入门
1.1 Spring简介 Spring是一个轻量级Java 企业级应用程序开发框架,目的是为了解决企业级应用开发的业务逻辑层和其他各层的耦合问题。它是一个分层的JavaSE/EEfull-stack(一站式) 轻量级开源框架,为开发Java应用程序提供全面的基础架构支持。 Spring Fra…...

【JavaEE Spring 项目】消息队列的设计
消息队列的设计 一、消息队列的背景知识二、需求分析核心概念⼀个⽣产者, ⼀个消费者N 个⽣产者, N 个消费者Broker Server 中的相关概念核⼼ API交换机类型 (Exchange Type)持久化⽹络通信消息应答 三、 模块划分四、 项⽬创建五、创建核心类创建 Exchange创建 MSGQUeue创建 B…...
SpringFramework学习笔记(Spring IoC,aop,tx)
SpringFramework 本篇笔记是基于尚硅谷学习资料的整理,涉及到其笔记的简化,补充,以及我在学习中遇到的与无法理解的问题及解决,如果想看完整及后续的笔记,可以去https://www.wolai.com/v5Kuct5ZtPeVBk4NBUGBWF查看官方…...

口腔管理平台 |基于springboot框架+ Mysql+Java+B/S结构的口腔管理平台 设计与实现(可运行源码+数据库+lw文档)
推荐阅读100套最新项目 最新ssmjava项目文档视频演示可运行源码分享 最新jspjava项目文档视频演示可运行源码分享 最新Spring Boot项目文档视频演示可运行源码分享 目录 前台功能效果图 管理员功能登录前台功能效果图 会员功能 系统功能设计 数据库E-R图设计 lunwen参考…...
)
【设计模式】Java 设计模式之工厂模式(Factory Pattern)
工厂模式(Factory Pattern)深入解析 一、工厂模式概述 工厂模式是一种创建型设计模式,它提供了一种封装对象创建过程的方式,将对象的创建与使用分离。工厂模式的核心思想是将“实例化对象”的操作与“使用对象”的操作分开&…...

安卓UI面试题 36-40
36. 简述 getDimension、getDimensionPixelOffset 和 getDimensionPixelSize 三者的区别? 相同点 单位为dp/sp时,都会乘以density,单位为px则不乘不同点 1、getDimension返回的是float值 2、getDimensionPixelSize,返回的是int值,float转成int时,四舍五入 3、getDimensio…...
Java有哪些常用的集合?
1、典型回答 在 Java 中,常用的集合有以下几个: 列表(List):有序集合,可以包含重复元素。常见实现类有 ArrayList、LinkedList、 Vector 等集合(Set):无序集合,不允许包含重复元素。常见实现类有 HashSet、…...

虚拟机网络链接
在虚拟网络设置中找到如下界面: "子网 IP" 192.168.79.0/24 表示一个局域网络,它有254个可能的IP地址可供分配(192.168.79.1到192.168.79.254),255.255.255.0 是子网掩码,定义了网络和主机部分。…...
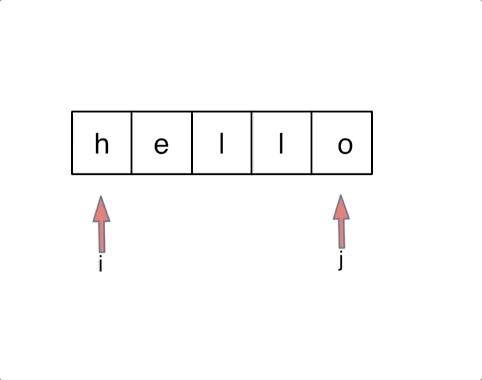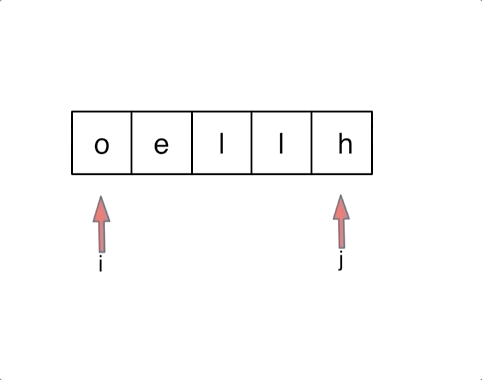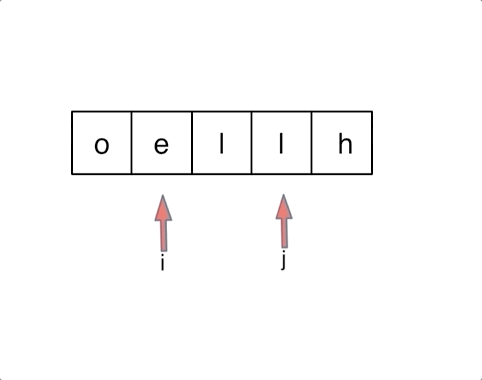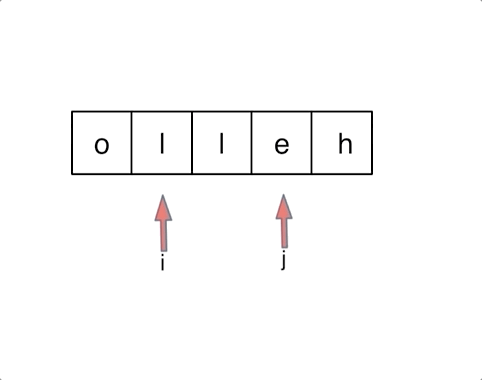
代码随想录阅读笔记-字符串【反转字符串】
题目 编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。 不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。 你可以假设数组中的所有字符都是 ASCII 码表中的可打印…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
