MySQL数据库实现增删改查基础操作
准备工作
- 安装mysql8.0+ (安装时一定要记住用户名和密码)
- 安装数据库可视化视图工具Navicat
请注意⚠️⚠️⚠️⚠️
a. 编程类所有软件不要安装在中文目录下
b. Navicat破解版下载安装教程:(由于文章审核提示版权问题,链接不方便给出)
第一步:打开Navicat 创建一个连接

请注意⚠️⚠️⚠️⚠️
设置连接名,用户名,和密码之后,一定要点击右下角【测试连接】按钮,来测试用户名和密码是否正确。如下图所示,弹出连接成功,说明连接mysql成功!!!

第二步:创建数据库名:取名叫student
鼠标选中test,然后右键选择【新建数据库】


到这里,数据库student创建成功
第三步:建表
鼠标选中【表】右键选择【新建表】,具体操作步骤如下图所示

然后根据自己的需求,添加表的字段,操作如下图所示
请注意⚠️⚠️⚠️⚠️
a. 每一表都应该有一个唯一的主键ID,并且是自主增长属性
b. 一定要按Ctrl+S保存,会弹出提示设置表名


第四步:编写增,删,改,查语句
- 新增
insert into student_table (student_name,student_class) values("张三","软件一班")
- 删除
delete from student_table where student_id =7
- 修改
update student_table set student_name='王武' where student_id =6
修改多个多个字端中间用逗号隔开’,’
update student_table set student_name='王武', student_class = '软件二班' where student_id =7
- 查询
select * from student_table
相关文章:

MySQL数据库实现增删改查基础操作
准备工作 安装mysql8.0 (安装时一定要记住用户名和密码)安装数据库可视化视图工具Navicat 请注意⚠️⚠️⚠️⚠️ a. 编程类所有软件不要安装在中文目录下 b. Navicat破解版下载安装教程:(由于文章审核提示版权问题,链接不方便给出ÿ…...
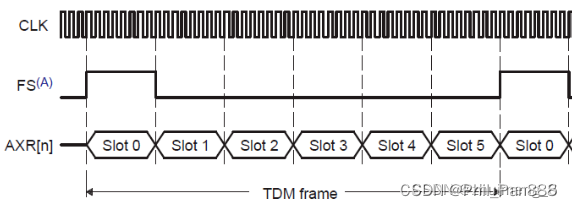
PCM和I2S区别
I2S和PCM接口都是数字音频接口,而所见的蓝牙到cpu以及codec的音频接口都是用PCM接口,是不是两个接口有各自不同的应用呢?先来看下概念。 PCM(PCM-clock、PCM-sync、PCM-in、PCM-out)脉冲编码调制,模拟语音信…...
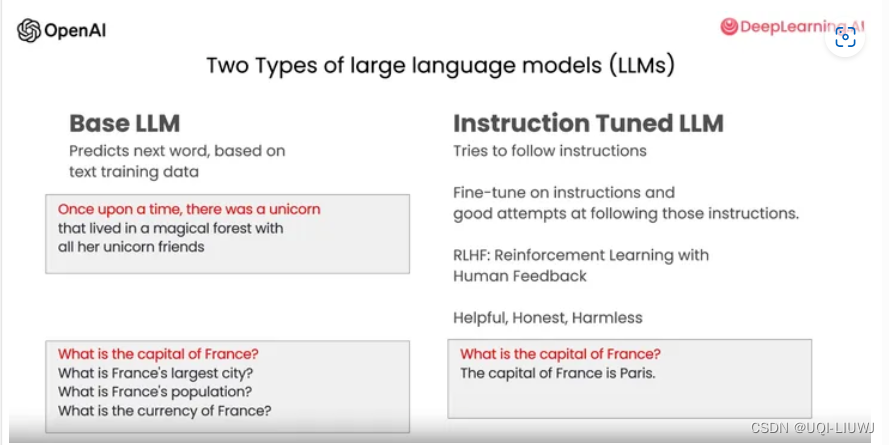
大模型笔记:吴恩达 ChatGPT Prompt Engineering for Developers(1) prompt的基本原则和策略
1 intro 基础大模型 VS 用指令tune 过的大模型 基础大模型 只会对prompt的文本进行续写 所以当你向模型发问的时候,它往往会像复读机一样续写几个问题这是因为在它见过的语料库文本(通常大多来自互联网)中,通常会连续列举出N个问…...

设计模式 — — 单例模式
一、是什么 单例模式只会在全局作用域下创建一次实例对象,让所有需要调用的地方都共享这一单例对象 二、实现 // 单例构造函数 function CreateSingleton (name) {this.name name;this.getName(); };// 获取实例的名字 CreateSingleton.prototype.getName func…...
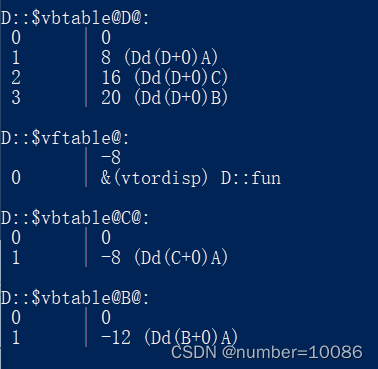
C++:菱形继承与虚继承
看下面这个示例代码 class A{ public: int num10; A(){cout<<"A构造"<<endl;} virtual void fun(){cout<<"A虚函数"<<endl;} };class B:public A{ public: B(){cout<<"B构造"<<endl;} void fun(){cout<…...

贡献法:USACO 2021 December Contest Bronze:孤独的照片
Farmer John 最近购入了 N 头新的奶牛,每头奶牛的品种是更赛牛(Guernsey)或荷斯坦牛(Holstein)之一。 奶牛目前排成一排,Farmer John 想要为每个连续不少于三头奶牛的序列拍摄一张照片。 然而,他…...

Java实现简单的通讯录
每日一言 泪眼问花花不语,乱红飞过秋千去。 —欧阳修- 简单的通讯录实现,跟写Java实现图书管理系统差不多,用到的知识也差不多,就当个小练习,练习一下写Java程序的手感。 Java实现图书管理系统 关于通讯录的代码都写…...

服务器数据恢复—raid5热备盘上线同步数据失败的如何恢复数据
服务器数据恢复环境&故障&分析: 一台存储上有一组由多块硬盘组建的raid5阵列,该raid5阵列中的一块硬盘掉线,热备盘自动上线同步数据的过程中,raid阵列中又有一块硬盘掉线,热备盘的数据同步被中断,r…...
探索C语言中的循环结构
循环结构是程序设计中一种重要的控制结构,它允许程序重复执行特定的代码块,直到满足某个条件为止。在C语言中,循环结构有多种形式,如for循环、while循环和do-while循环。本文将介绍C语言中的循环结构,并讨论它们的用法…...

数学建模-估计出租车的总数
文章目录 1、随机抽取的号码在总体的排序 1、随机抽取的号码在总体的排序 10个号码从小到大重新排列 [ x 0 , x ] [x_0, x] [x0,x] 区间内全部整数值 ~ 总体 x 1 , x 2 , … , x 10 总体的一个样本 x_1, x_2, … , x_{10} ~ 总体的一个样本 x1,x2,…,x10 总体的一个样…...

设计模式在芯片验证中的应用——装饰器
一、装饰器模式 装饰器模式(Decorator)是一种结构化软件设计模式,它提供了一种通过向类对象添加行为来修改类对象的方法,而不会影响同一类的其它对象行为。该模式允许在不修改抽象类的情况下添加类功能。它从本质上允许基类代码对不可预见的修改具有前瞻…...

Python 查找并高亮PDF中的指定文本
在处理大量PDF文档时,有时我们需要快速找到特定的文本信息。本文将提供以下三个Python示例来帮助你在PDF文件中快速查找并高亮指定的文本。 查找并高亮PDF中所有的指定文本查找并高亮PDF某个区域内的指定文本使用正则表达式搜索指定文本并高亮 本文将用到国产第三方…...

LEETCODE LCS 03. 主题空间
题目描述如上,这个题主要运用了DFS的思想,同时走过的路径标记为6,即可在后续的遍历中过滤掉重复的元素,其他则类似边界条件的判断和题目条件的判断,求最大值,只需要一次遍历中累加对比每一次得即可。 模板&…...
【Spring Boot 源码学习】深入应用上下文初始化器实现
《Spring Boot 源码学习系列》 深入应用上下文初始化器实现 一、引言二、往期内容三、主要内容3.1 spring-boot 子模块中内置的实现类3.1.1 ConfigurationWarningsApplicationContextInitializer3.1.2 ContextIdApplicationContextInitializer3.1.3 DelegatingApplicationConte…...
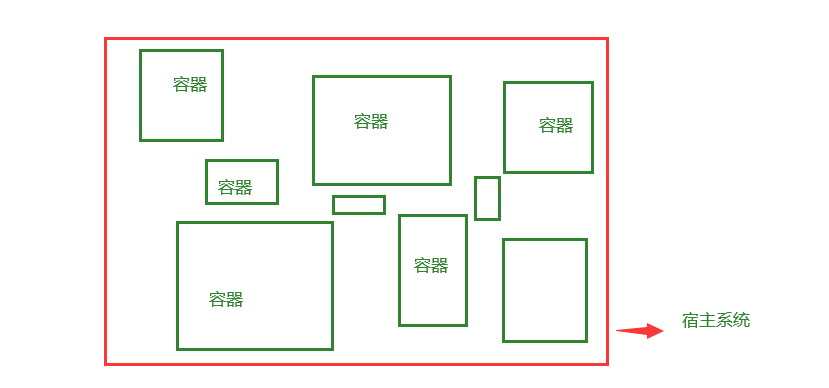
【Docker】一文趣谈Docker
🏡浩泽学编程:个人主页 🔥 推荐专栏:《深入浅出SpringBoot》《java对AI的调用开发》 《RabbitMQ》《Spring》《SpringMVC》《项目实战》 🛸学无止境,不骄不躁,知行合一 文章目录 …...
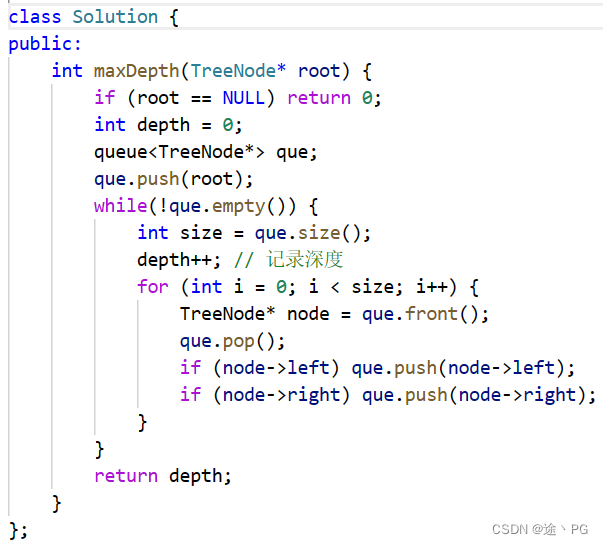
代码随想录day19(2)二叉树:二叉树的最大深度(leetcode104)
题目要求:求出二叉树的最大深度 思路:首先要区分二叉树的高度与深度。二叉树的高度是任一结点到叶子结点的距离,而二叉树的深度指的是任一节点到根节点的距离(从1开始)。所以求高度使用后序遍历(从下往上&…...
)
Lua中文语言编程源码-第五节,更改lcorolib.c协程库函数, 使Lua加载中文库关键词(与所有的基础库相关)
源码已经更新在CSDN的码库里: git clone https://gitcode.com/funsion/CLua.git 在src文件夹下的lcorolib.c协程库函数,Coroutine Library:表明这个C源文件实现了Lua的协程库(Coroutine Library),即提供了…...
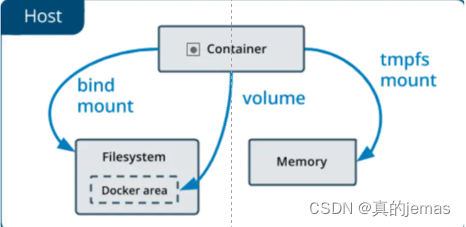
Docker学习之数据管理(超详解析)
Docker存储资源类型: 用户在使用 Docker 的过程中,势必需要查看容器内应用产生的数据,或者需要将容器内数据进行备份,甚至多个容器之间进行数据共享,这必然会涉及到容器的数据管理: (1ÿ…...

FDTD液晶折射率各项异性表示方法
由于FDTD的数据都是沿坐标轴的,各向异性材料的参数也需要根据坐标轴来输入。 首先要了解坐标变换。 坐标变换 这里以二维坐标变化为例。 矢量下我们可以发现OP可在两个坐标系下分别表示 接下来将两个坐标相互关联,这里以Xb举例,Yb同理 注…...
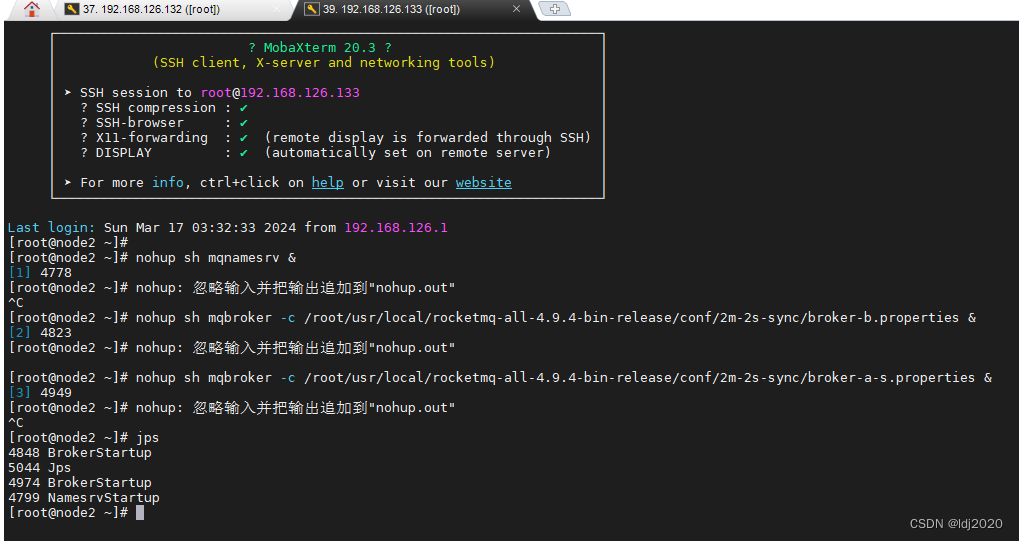
RoketMQ主从搭建
vim /etc/hosts# IP与域名映射,端口看自己的#nameserver 192.168.126.132 rocketmq-nameserver1 192.168.126.133 rocketmq-nameserver2# 注意主从节点不在同一个主机上 #broker 192.168.126.132 rocketmq-master1 192.168.126.133 rocketmq-master2#broker 192.168…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
