Python可变对象与不可变对象的浅拷贝与深拷贝
前言
本文主要介绍了python中容易面临的考试点和犯错点,即浅拷贝与深拷贝
首先,针对Python中的可变对象来说,例如列表,我们可以通过以下方式进行浅拷贝和深拷贝操作:
import copya = [1, 2, 3, 4, ['a', 'b']]b = a # 赋值,将变量a赋值给变量b
c = a.copy() # 浅拷贝, 或者 c = copy.copy(a)
d = copy.deepcopy(a) # 深拷贝print(a) # [1, 2, 3, 4, ['a', 'b']]
print(b) # [1, 2, 3, 4, ['a', 'b']]
print(c) # [1, 2, 3, 4, ['a', 'b']]
print(d) # [1, 2, 3, 4, ['a', 'b']]
我们可以发现,赋值、浅拷贝和深拷贝后的变量的值是一样的,但他们的“内部”真的一样吗?
本文就是回答这个问题的
参考
本文主要参考了哔哩哔哩视频:十分钟!彻底弄懂Python深拷贝与浅拷贝机制
是视频里,up主推荐了一个神奇,即pythontutor
列表(list)
结论
为了探究前言中提到的a,b,c,d是个变量是否真的一样,我们借助pythontutor来进行可视化,从内存的角度来进行探究

结论:
赋值:变量b和a是完全一样的,即他们完全共享同一个内存空间,a变,b也会跟着变。
浅拷贝:变量c只有跟a共享第二级的列表,而不共享第一级列表的内容,即改变a的第一层列表内容,c不会变,而改变a第二层列表的内容,c就会跟着变了。
深拷贝:变量d和a完全不共享任何内存,d完全是新开辟了一个新的空间,即可认为d和a是完全没有关系的,改变a或者d都不会影响对方。
测试
import copya = [1, 2, 3, 4, ['a', 'b']]
b = a
c = copy.copy(a)
d = copy.deepcopy(a)print('a:', a) # [1, 2, 3, 4, ['a', 'b']]
print('b:', b) # [1, 2, 3, 4, ['a', 'b']]
print('c:', c) # [1, 2, 3, 4, ['a', 'b']]
print('d:', d) # [1, 2, 3, 4, ['a', 'b']]a.append(5)
a[4].append('c')print('a:', a) # [1, 2, 3, 4, ['a', 'b', 'c'], 5]
print('b:', b) # [1, 2, 3, 4, ['a', 'b', 'c'], 5]
print('c:', c) # [1, 2, 3, 4, ['a', 'b', 'c']]
print('d:', d) # [1, 2, 3, 4, ['a', 'b']]
结果:

这里的结果也不用多解释了,完全符合前面的结论
元组(tuple)
由于元组是不可变对象,那它的浅拷贝与深拷贝会一样吗?例如:
import copya = (1, 2, 3, 4, ('a', 'b'))
b = a
c = copy.copy(a)
d = copy.deepcopy(a)print('a:', a)
print('b:', b)
print('c:', c)
print('d:', d)
还是直接去看内存空间

结论:
对于元组来说,赋值、浅拷贝与深拷贝没有区别,都共享同一个内存,这也很好理解,因为元组是不可变对象,是无法对变量a进行修改的
列表与元组混合
列表里面嵌套元组
import copya = [1, 2, 3, 4, ('a', 'b')]
b = a
c = copy.copy(a)
d = copy.deepcopy(a)print('a:', a)
print('b:', b)
print('c:', c)
print('d:', d)
内存情况:

结论:
就算是深拷贝,元组部分都是共享内存的
元组里面嵌套列表
import copya = (1, 2, 3, 4, ['a', 'b'])
b = a
c = copy.copy(a)
d = copy.deepcopy(a)print('a:', a)
print('b:', b)
print('c:', c)
print('d:', d)
内存情况:

结论:
完全同列表的情况
相关文章:

Python可变对象与不可变对象的浅拷贝与深拷贝
前言 本文主要介绍了python中容易面临的考试点和犯错点,即浅拷贝与深拷贝 首先,针对Python中的可变对象来说,例如列表,我们可以通过以下方式进行浅拷贝和深拷贝操作: import copya [1, 2, 3, 4, [a, b]]b a …...
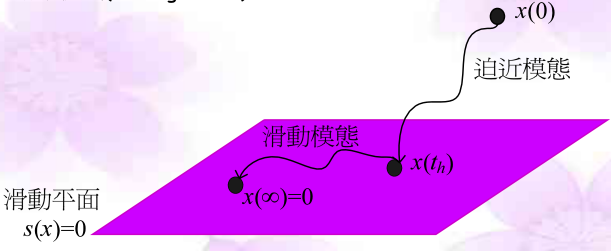
滑模控制(Sliding mode control)快速入门
0. 简介 最近作者受到邀请,让我帮忙给刚入门的学弟讲讲滑模控制。可是作者也不知道怎么向未入门的学弟讲解这些基础知识,所以作者翻了翻近几年写的很好的文章以及视频。综合起来,来总结出一套比较基础,且适用于初学者的文章吧。这…...
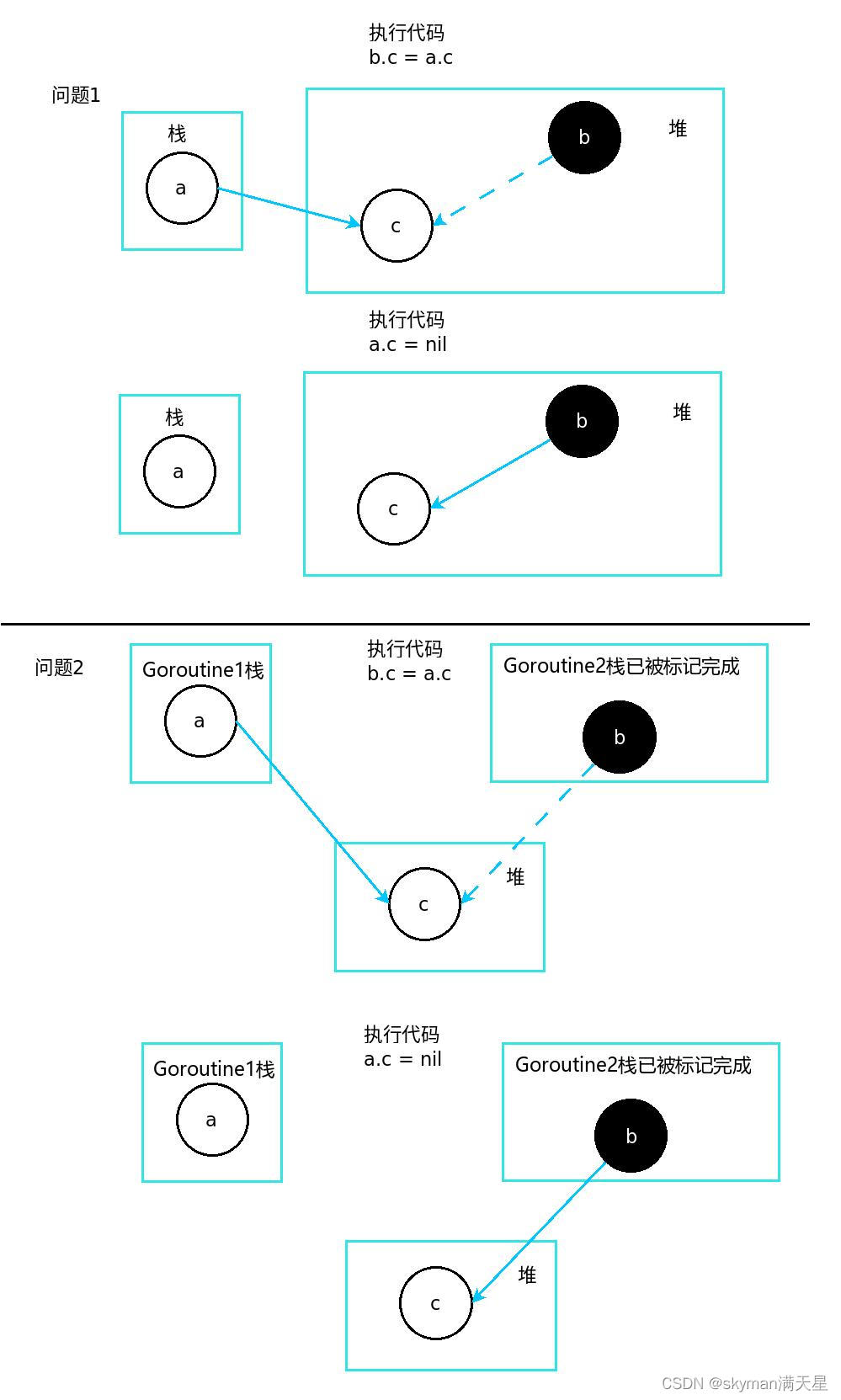
golang的垃圾回收详解
golang的垃圾回收详解 一、三色标记法 作为一门现代化的语言,golang与java一样,都在语言中内置了垃圾回收的功能,不需要程序员自己去回收堆内存。而垃圾回收中,最重要的两个部分就是垃圾检测算法以及垃圾回收算法。垃圾检测算法决…...
线上负载过高排查(top/vmstat/ifstat/free/df)
目录 一、五大命令 二、故障排查步骤 1、top命令找出CPU占比最高的 2、ps -ef 或者 jps -l进一步定位 3、ps -mp位到具体线程或者代码 4、jstack精准定位到错误的地方 本文通过学习:周阳老师-尚硅谷Java大厂面试题第二季 总结的LinuxJDK命令操作相关的笔记 一…...
Java的注解(Annotation)
Java 注解(Annotation)又称 Java 标注,是 JDK5.0 引入的一种注释机制。Java 中的类、构造器、方法、成员变量、参数等都可以被注解进行标注。例如JUnit单元测试中的Test方法,可以使得方法直接运行。JUnit单元测试Test单元测试是针…...

信息系统项目管理师:配置管理
配置管理指的是在一个系统或软件中对配置项的管理,包括对配置项的定义、存储、跟踪和修改等一系列活动。配置项可以是硬件设备、软件组件、系统设置、网络配置等,配置管理旨在确保在不同时间点或环境下系统或软件的配置项的正确性和一致性。通过配置管理…...
web餐饮开源程序
简介 一款专门针对餐饮行业而开发桌面应用程序 技术 借助Panuon.UI.Silver控件库,开发的一款餐饮软件。 运行环境:.NETFramework,Versionv4.8。 运行数据库:MySql。 ORM框架:SqlSugar。 第三方插件:Panuon.UI.Silv…...
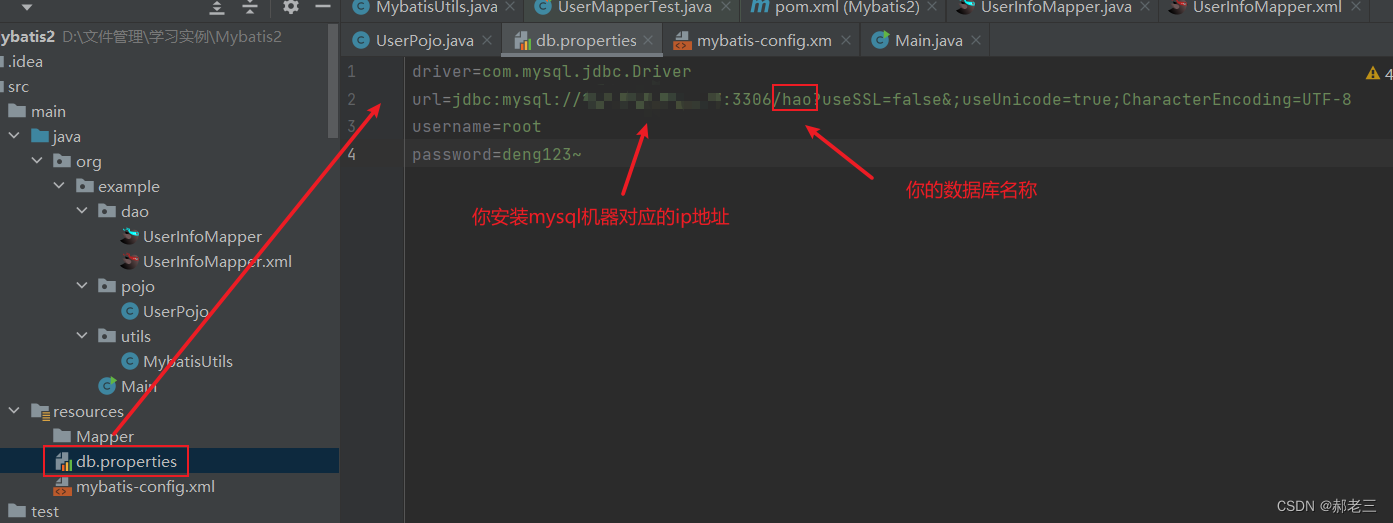
28个案例问题分析---027---单表的11个Update接口--MyBatis
一:背景介绍 项目开发中。我们使用的是MyBatis,在MyBatis的xml文件里,两个表的更新功能,写了足足11个更新接口,毫无复用的思想 这种方式可以正常的实现功能,但是没有复用,无论是从时间上还是维…...

大数据开发治理平台 DataWorks
序言学习下阿里DataWorks的设计理念以及要做的事情cuiyaonan2000163.com参考文档:https://www.aliyun.com/product/bigdata/idehttps://help.aliyun.com/document_detail/73015.htmlhttps://help.aliyun.com/document_detail/324149.html ----数据治理LaunchDataWorks基于阿里云…...

Xshell的下载、使用、配置【ssh、telnet、串口】
目录 一、概述 二、Xshell的使用 2.1 Xshell使用ssh协议远程连接Linux主机或服务器 2.2 Xshell使用telnet协议远程连接Linux开发板 2.3 Xshell使用SERIAL协议远程连接Linux开发板 三、Xshell常用配置 3.1 配置默认会话属性 一、概述 Xshell是由NetSarang公司开发的强大…...
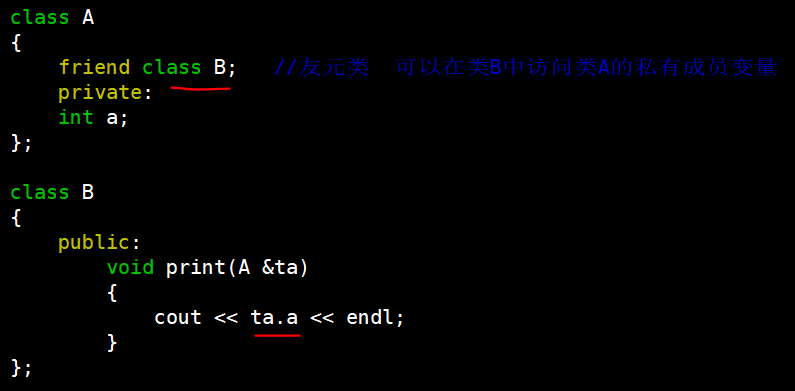
C++回顾(七)—— 面向对象模型
7.1 静态成员变量和静态成员函数 7.1.1 静态成员变量 关键字 static 可以用于说明一个类的成员;静态成员提供了一个同类对象的共享机制;把一个类的成员说明为 static 时,这个类无论有多少个对象被创建,这些对象共享这个 static …...

开源监控服务uptime-kuma
好久没写文章了,刚好最近用了一个开源的监控服务,感觉蛮有意思的,记录一下 (一)安装 uptime-kuma安装方式有几种,这里当然是选择大家都爱的docker,一条命令搞定 docker run -d --restartalways -p 3001:…...

JavaScript混淆技术:了解其核心原理和常用手段
当今互联网时代,JavaScript已经成为了web前端开发的重点技术之一。其中,JavaScript代码的安全性问题一直是关注的焦点。为了保护JavaScript代码的安全性,很多人对其进行加密处理,众所周知,对于单纯的加密算法ÿ…...

大型医院云HIS系统:采用前后端分离架构,前端由Angular语言、JavaScript开发;后端使用Java语言开发 融合B/S版电子病历系统
一套医院云his系统源码 采用前后端分离架构,前端由Angular语言、JavaScript开发;后端使用Java语言开发。融合B/S版电子病历系统,支持电子病历四级,HIS与电子病历系统均拥有自主知识产权。 文末卡片获取联系! 基于云计…...
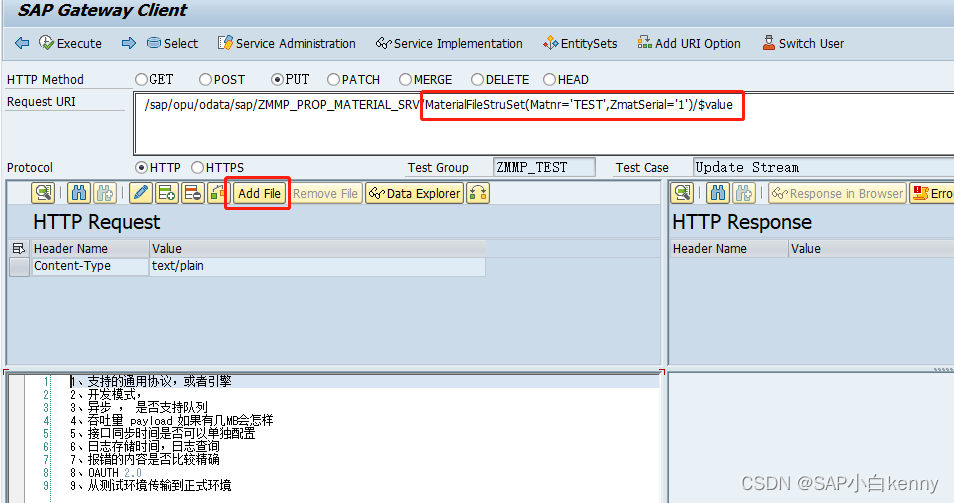
SAP UI5 Upload/Download file through NetWeaver Gateway
1、创建 SEGW对象 2、创建Entity Type 要把Media 标识打上 3、 激活对象然后到DPC Class的扩展对象里面重定义 /IWBEP/IF_MGW_APPL_SRV_RUNTIME~GET_STREAM /IWBEP/IF_MGW_APPL_SRV_RUNTIME~CREATE_STREAM /IWBEP/IF_MGW_APPL_SRV_RUNTIME~UPDATE_STREAM METHOD /iwbep/if_m…...
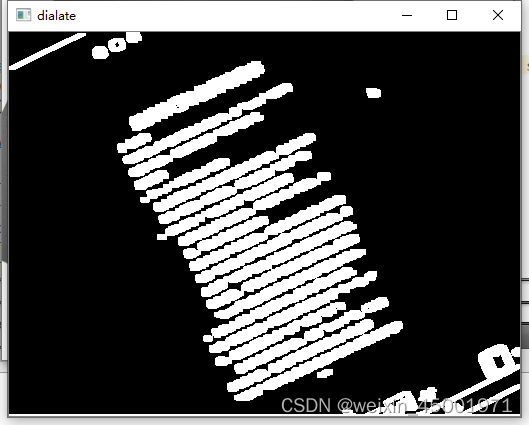
opencv校正图像
目录1、前言2、例程2.1、代码2.2、效果口罩说明书网页3、按步骤分析转灰度图降噪 Canny边缘检测膨胀(可视具体情况省略)轮廓检索选取角度1、前言 我们用相机拍照时,会因为角度问题造成拍歪,会影响图像的识别,这时就需…...

JavaScript:函数与箭头函数的区别
ref 1. 定义 函数 function getName() {}箭头函数 const getName () > {}2. 命名 函数分为匿名、具名。 function getName() {} let getName function () {}箭头函数只有匿名。 const getName () > {}3. 构造函数 箭头函数都是匿名函数,所以不能作为构造…...
)
八股文(四)
目录 一、 Vue2的双向数据绑定原理 二、 vue2数据绑定缺点是什么?vue3是怎么解决的? (1)因为vue2.0 object.defineProperty只能劫持对象属性 (2)Proxy是直接代理对象 (3)proxy不…...
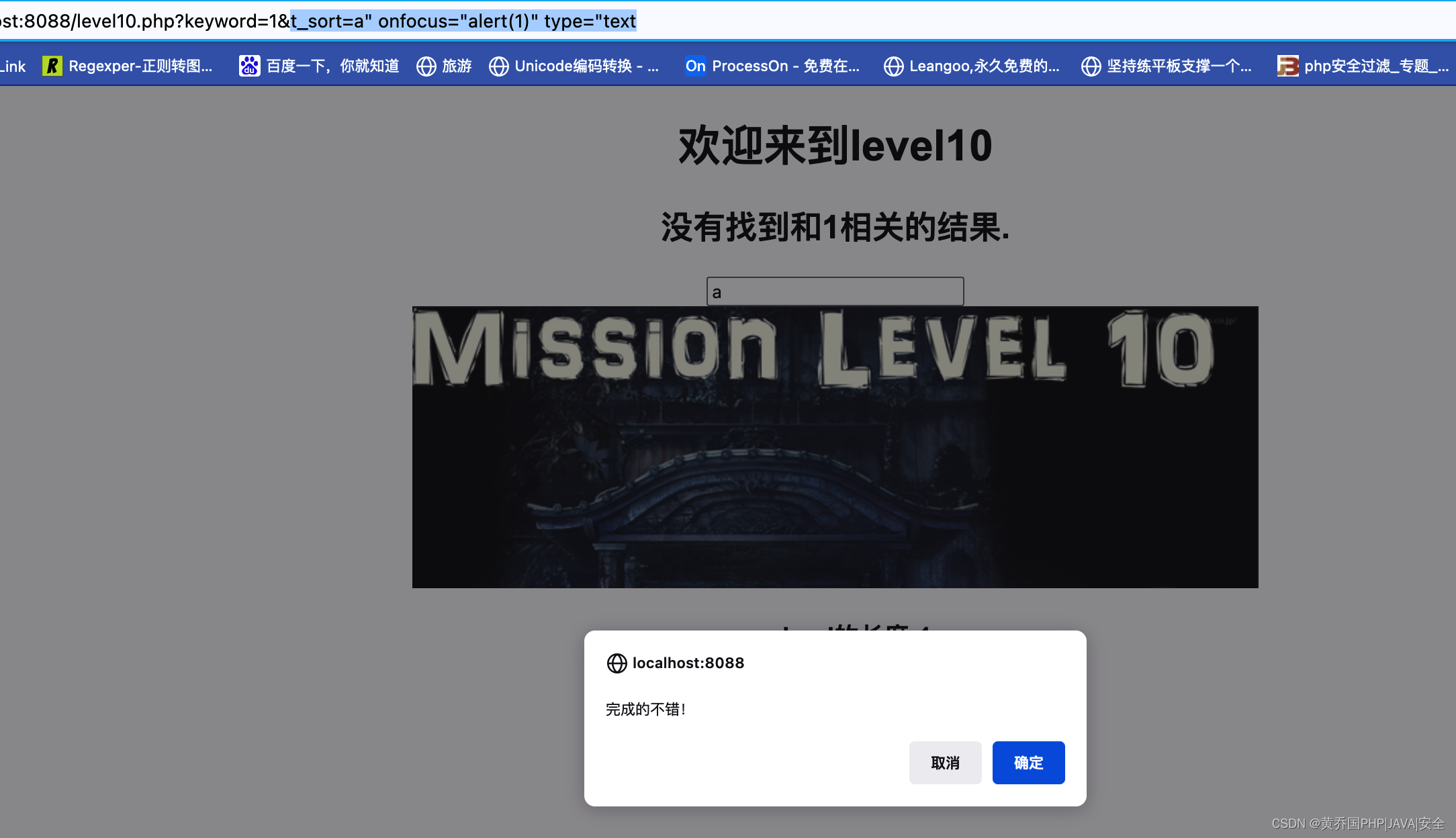
XSS挑战赛(xsslabs)1~10关通关解析
简介 XSS挑战赛,里面包含了各种XSS的防御方式和绕过方式,好好掌握里面的绕过细节,有助于我们更好的去发现XSS漏洞以及XSS的防御。本文更多的是分享解析的细节,不是一个标准的答案,希望大家在渗透的时候有更多的思维。…...
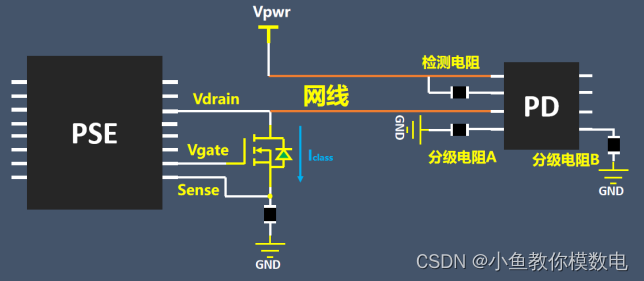
什么是以太网供电POE
POE指的是以太网供电,就是一根网线在传输网络的同时还传输设备所需的电源。我们最常见的就是通过POE交换机连接网络摄像头,网络摄像头无需的电源适配器,仅靠一根网线就能实现电源和网络的传输。POE供电一般可以到100米。POE包含两个部分&…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
