[二分查找]LeetCode2040:两个有序数组的第 K 小乘积
本文涉及的基础知识点
二分查找算法合集
题目
给你两个 从小到大排好序 且下标从 0 开始的整数数组 nums1 和 nums2 以及一个整数 k ,请你返回第 k (从 1 开始编号)小的 nums1[i] * nums2[j] 的乘积,其中 0 <= i < nums1.length 且 0 <= j < nums2.length 。
示例 1:
输入:nums1 = [2,5], nums2 = [3,4], k = 2
输出:8
解释:第 2 小的乘积计算如下:
- nums1[0] * nums2[0] = 2 * 3 = 6
- nums1[0] * nums2[1] = 2 * 4 = 8
第 2 小的乘积为 8 。
示例 2:
输入:nums1 = [-4,-2,0,3], nums2 = [2,4], k = 6
输出:0
解释:第 6 小的乘积计算如下: - nums1[0] * nums2[1] = (-4) * 4 = -16
- nums1[0] * nums2[0] = (-4) * 2 = -8
- nums1[1] * nums2[1] = (-2) * 4 = -8
- nums1[1] * nums2[0] = (-2) * 2 = -4
- nums1[2] * nums2[0] = 0 * 2 = 0
- nums1[2] * nums2[1] = 0 * 4 = 0
第 6 小的乘积为 0 。
示例 3:
输入:nums1 = [-2,-1,0,1,2], nums2 = [-3,-1,2,4,5], k = 3
输出:-6
解释:第 3 小的乘积计算如下: - nums1[0] * nums2[4] = (-2) * 5 = -10
- nums1[0] * nums2[3] = (-2) * 4 = -8
- nums1[4] * nums2[0] = 2 * (-3) = -6
第 3 小的乘积为 -6 。
参数范围:
1 <= nums1.length, nums2.length <= 5 * 104
-105 <= nums1[i], nums2[j] <= 105
1 <= k <= nums1.length * nums2.length
nums1 和 nums2 都是从小到大排好序的。
两层二分查找
时间复杂度
O(log(max2)nlogn),n是两个数组长度的较大者,max 是两个数组的最大值。
分情况讨论
| 结果 | 数组一 | 数组二 |
|---|---|---|
| 负数 | 负数 | 正数 |
| 负数 | 正数 | 负数 |
| 0 | 0 | 任意数 |
| 0 | 非0 | 0 |
| 正数 | 正数 | 正数 |
| 正数 | 负数 | 负数 |
第一层二分
寻找一个符合如下条件的llMul:
乘积小于等于llMul的组合数量大于等于k。
左开右闭空间。
负数的问题
如果乘积为负数,第k小则绝对值第k大。我们可以负数全部转成绝对值,然后倒序,这样可以保证升序。m个数,第k大(从1开始),就是m-k+1小。
变量解释
| v11 | 数组一中的负数的绝对值,升序 |
| v12 | 数组一中的正数,升序 |
| v21 | 数组二中的负数的绝对值,升序 |
| v22 | 数组二中的正数,升序 |
代码
核心代码
class Solution {
public:
long long kthSmallestProduct(vector& nums1, vector& nums2, long long k) {
auto it1 = std::equal_range(nums1.begin(), nums1.end(), 0);
auto it2 = std::equal_range(nums2.begin(), nums2.end(), 0);
const long long less0Count1 = it1.first - nums1.begin();
const long long i0Count1 = it1.second - it1.first;
const long long great0Count1 = nums1.end() - it1.second;
const long long less0Count2 = it2.first - nums2.begin();
const long long i0Count2 = it2.second - it2.first;
const long long great0Count2 = nums2.end() - it2.second;
const long long llZeroCount = i0Count1 * nums2.size() + i0Count2 * nums1.size() - i0Count1 * i0Count2;
const long long llLess0Cout = less0Count1 * great0Count2 + less0Count2 * great0Count1;
vector v12(it1.second, nums1.end());
vector v22(it2.second, nums2.end());
vector v11 = CopyAndMul(vector(nums1.begin(), it1.first));
vector v21 = CopyAndMul(vector(nums2.begin(), it2.first));
if (k <= llLess0Cout)
{//在负数中找
k = llLess0Cout + 1 - k;
return -DoGreate0(v11, v22, v21, v12, k);
}
k -= llLess0Cout;
if (k <= llZeroCount)
{
return 0;
}
k -= llZeroCount;
return DoGreate0(v11, v21,v12, v22,k);
}
//从升序正数数组中寻找第k小的积: 第一个积小于等于llMul 的数量大于等于k 左开右闭
long long DoGreate0(const vector& nums11,const vector& nums12, const vector& nums21, const vector& nums22, long long k)
{
long long left = 0, right = (long long) 1e10;
while (right - left > 1)
{
const auto mid = left + (right - left) / 2;
int iCnt = 0;
const long long llHas = LessEqual(nums11, nums12, mid) + LessEqual(nums21, nums22, mid);
if (llHas >= k)
{
right = mid;
}
else
{
left = mid;
}
}
return right;
}
long long LessEqual(const vector& nums1, const vector& nums2, long long llMul)
{
long long llCnt = 0;
for (const auto& n : nums2)
{
llCnt += std::upper_bound(nums1.begin(), nums1.end(), llMul / n) - nums1.begin();
}
return llCnt;
}
vector CopyAndMul(const vector& nums)
{
vector vRet(nums.size());
for (int i = 0; i < nums.size(); i++)
{
vRet[i] = -nums[nums.size() - 1 - i];
}
return vRet;
}
};
测试用例
template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
assert(v1[i] == v2[i]);
}
}
template
void Assert(const T& t1, const T& t2)
{
assert(t1 == t2);
}
int main()
{
vector nums1, nums2;
long long k, res;
{
nums1 = { -2,-1 }, nums2 = { -2,-1 }, k = 4;
Solution slu;
auto res = slu.kthSmallestProduct(nums1, nums2, k);
Assert(4LL, res);
}
{
nums1 = { 2, 5 }, nums2 = { 3, 4 }, k = 2;
Solution slu;
auto res = slu.kthSmallestProduct(nums1, nums2, k);
Assert(8LL, res);
}
{
nums1 = { -4,-2,0,3 }, nums2 = { 2,4 }, k = 6;
Solution slu;
auto res = slu.kthSmallestProduct(nums1, nums2, k);
Assert(0LL, res);
}
{
nums1 = { -2,-1,0,1,2 }, nums2 = { -3,-1,2,4,5 }, k = 3;
Solution slu;
auto res = slu.kthSmallestProduct(nums1, nums2, k);
Assert(-6LL, res);
}
{
nums1 = { 0 }, nums2 = { 0,0,0}, k = 3;
Solution slu;
auto res = slu.kthSmallestProduct(nums1, nums2, k);
Assert(0LL, res);
}
{
nums1 = { 1,2 }, nums2 = { 1,2}, k = 3;
Solution slu;
auto res = slu.kthSmallestProduct(nums1, nums2, k);
Assert(2LL, res);
}
{
nums1 = { 1,10000 };
nums2 = { 1,10000 };
k = 4;
Solution slu;
auto res = slu.kthSmallestProduct(nums1, nums2, k);
Assert(10000* 10000LL, res);
}
//CConsole::Out(res);
}
优化一
确保数组二的长度比数组一短
if (nums1.size() < nums2.size()){swap(nums1, nums2);}
完整函数:
long long LessEqual( vector<int>& nums1, vector<int>& nums2, long long llMul){if (nums1.size() < nums2.size()){swap(nums1, nums2);}long long llCnt = 0;for (const auto& n : nums2){llCnt += std::upper_bound(nums1.begin(), nums1.end(), llMul / n) - nums1.begin();}return llCnt;}
优化二
第二层二分查找可以优化成双指针。这样也不用思考取整之类,容易理解。
long long LessEqual( vector<int>& nums1, vector<int>& nums2, long long llMul){long long llCnt = 0;int right = nums1.size()-1;for (const auto& n : nums2){while ((right >=0 ) && (nums1[right] * (long long)n > llMul)){//nums1[0,right]*n 全部小于等于llMulright--;}llCnt += (right+1);}return llCnt;}
优化三
0不必单独考虑。0符合负数的规则:绝对值越大,乘积越小。0也符合正数的规则,觉得值越大,乘积越大。
class Solution {
public:long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {auto it1 = std::lower_bound(nums1.begin(), nums1.end(), 0);auto it2 = std::lower_bound(nums2.begin(), nums2.end(), 0);vector<int> v12(it1, nums1.end());vector<int> v22(it2, nums2.end());vector<int> v11 = CopyAndMul(vector<int>(nums1.begin(), it1));vector<int> v21 = CopyAndMul(vector<int>(nums2.begin(), it2));const long long ll24Count = v11.size() * (long long)v22.size() + (long long)v12.size() * v21.size();if (k <= ll24Count){//在负数中找k = ll24Count + 1 - k;return -DoGreate0(v11, v22, v21, v12, k);}k -= ll24Count; return DoGreate0(v11, v21,v12, v22,k);}//从升序正数数组中寻找第k小的积: 第一个积小于等于llMul 的数量大于等于k 左开右闭long long DoGreate0( vector<int>& nums11, vector<int>& nums12, vector<int>& nums21, vector<int>& nums22, long long k){long long left = -1, right = (long long) 1e10;while (right - left > 1){const auto mid = left + (right - left) / 2;const long long llHas = LessEqual(nums11, nums12, mid) + LessEqual(nums21, nums22, mid);if (llHas >= k){right = mid;}else{left = mid;}}return right;}long long LessEqual( vector<int>& nums1, vector<int>& nums2, long long llMul){long long llCnt = 0;int right = nums1.size()-1;for (const auto& n : nums2){while ((right >=0 ) && (nums1[right] * (long long)n > llMul)){//nums1[0,right]*n 全部小于等于llMulright--;}llCnt += (right+1);}return llCnt;}vector<int> CopyAndMul(const vector<int>& nums){vector<int> vRet(nums.size());for (int i = 0; i < nums.size(); i++){vRet[i] = -nums[nums.size() - 1 - i];}return vRet;}
};
2023年3月版
class CNumHelp
{
public:
CNumHelp(vector& nums) :m_nums(nums)
{
auto it1 = std::equal_range(m_nums.begin(), m_nums.end(), 0);
m_iLess0Num = it1.first - m_nums.begin();
m_i0Num = it1.second - it1.first;
m_iMore0Num = m_nums.end() - it1.second;
m_iLessEqual0Num = m_iLess0Num + m_i0Num;
m_iMoreEqualNum = m_iMore0Num + m_i0Num;
}
vector m_nums;
int m_iLess0Num = 0, m_i0Num = 0, m_iMore0Num = 0;
int m_iLessEqual0Num = 0,m_iMoreEqualNum=0;
};
class ICal
{
public:
virtual long long Cal(long long llMid)const = 0;
};
class CCalMore0 : public ICal
{
public:
CCalMore0(const CNumHelp& help1, const CNumHelp& help2) :m_help1(help1), m_help2(help2)
{
}virtual long long Cal(long long llMid)const{long long llNum = 0;for (int i = m_help1.m_iLessEqual0Num; i < m_help1.m_nums.size(); i++){int iCurNum = std::upper_bound(m_help2.m_nums.begin(), m_help2.m_nums.end(), llMid / m_help1.m_nums[i]) - m_help2.m_nums.begin() - m_help2.m_iLessEqual0Num;llNum += iCurNum;}for (int i = 0; i < m_help1.m_iLess0Num; i++){auto it = std::equal_range(m_help2.m_nums.begin(), m_help2.m_nums.end(), llMid / m_help1.m_nums[i]);//auto it2 = (0 == llMid % m_help1.m_nums[i]) ? it.first : it.second;auto it2 = it.first;llNum += m_help2.m_nums.end() - it2 - m_help2.m_iMoreEqualNum;}return llNum;}
private:
const CNumHelp m_help1;const CNumHelp m_help2;
};
class CCalLess0 : public ICal
{
public:
CCalLess0(const CNumHelp& help1, const CNumHelp& help2) :m_help1(help1), m_help2(help2)
{
}
virtual long long Cal(long long llMid)const
{
return Cal(llMid, m_help1, m_help2) + Cal(llMid, m_help2, m_help1);
}
static long long Cal(long long llMid, const CNumHelp& help1, const CNumHelp& help2)
{
long long llNum = 0;
for (int i = help1.m_iLessEqual0Num; i < help1.m_nums.size(); i++)
{
auto it = std::equal_range(help2.m_nums.begin(), help2.m_nums.end(), llMid / help1.m_nums[i]);
auto it2 = (0 == llMid% help1.m_nums[i]) ? it.second : it.first;
int iCurNum = it2 -help2.m_nums.begin();
llNum += iCurNum;
}
return llNum;
}
private:
const CNumHelp m_help1;
const CNumHelp m_help2;
};
class Solution {
public:
long long kthSmallestProduct(vector& nums1, vector& nums2, long long k) {
CNumHelp help1(nums1), help2(nums2);
//const long long llTotal = (long long)nums1.size()nums2.size();
const long long ll0Num = (long long)help1.m_i0Num * nums2.size() + (long long)help2.m_i0Num * nums1.size() - (long long)help1.m_i0Numhelp2.m_i0Num;
const long long llLess0Num = (long long)help1.m_iMore0Num * help2.m_iLess0Num + (long long)help1.m_iLess0Num * help2.m_iMore0Num;
if (k <= llLess0Num)
{
CCalLess0 cal(help1, help2);
return Do(cal, k, (long long)100000 * -100000 - 1,-1);
}
k -= llLess0Num;
if (k <= ll0Num)
{
return 0;
}
k -= ll0Num;
CCalMore0 cal(help1, help2);
return Do(cal, k, 0, (long long)100000 * 100000);
}
long long Do(const ICal& cal, long long k, long long left, long right)
{
while (right > left + 1)
{
const auto llMid = left + (right - left) / 2;
const long long llNum = cal.Cal(llMid);
if (llNum >= k)
{
right = llMid;
}
else
{
left = llMid;
}
}
return right;
}
};
2023年9月
class Solution {
public:
long long kthSmallestProduct(const vector& nums1, const vector& nums2, long long k) {
CalRange(nums1, m_v11, m_v12);
CalRange(nums2, m_v21, m_v22);
const int iZero1Num = nums1.size() - m_v11.size() - m_v12.size();
const int iZero2Num = nums2.size() - m_v21.size() - m_v22.size();
long long llLess0 = (long long)m_v11.size() * m_v22.size() + (long long)m_v21.size() * m_v12.size();
long long ll0 = (long long)nums2.size() * iZero1Num + (long long)nums1.size() * iZero2Num - (long long)iZero1Num * iZero2Num;
if (k <= llLess0)
{//结果是负数
m_v21.swap(m_v22);
return -Do(llLess0 - k + 1);
}
k -= llLess0;
if (k <= ll0)
{
return 0;
}
k -= ll0;
return Do(k);
}
long long Do(long long k)
{
long long left =-(1e10 + 0.5)-1, r = 1e10 + 0.5;
while (r - left > 1)
{
const auto mid = left + (r - left) / 2;
long long llNum = CountEqualLess(m_v11, m_v21,mid) + CountEqualLess(m_v12, m_v22,mid);
if (llNum >= k)
{
r = mid;
}
else
{
left = mid;
}
}
return r;
}
long long CountEqualLess(const vector& nums1, const vector& nums2, long long llMul)
{
long long llCnt = 0;
int r = 0 ;//[0,r)和num2[i]的乘积 < llMul
for (int i =nums2.size()-1; i >= 0 ;i-- )
{
for (; (r < nums1.size() ) && ((long long)nums1[r] * nums2[i] <= llMul); r++);
llCnt += r;
}
return llCnt;
}
static void CalRange(const vector& nums, vector& v1, vector& v2)
{
int i = 0;
for (i = 0; (i < nums.size()) && (nums[i] < 0); i++)
{
v1.emplace_back(-nums[i]);
}
std::reverse(v1.begin(), v1.end());
for (; (i < nums.size()) && (nums[i] == 0); i++);
for (; i < nums.size(); i++)
{
v2.emplace_back(nums[i]);
}
}
vector m_v11, m_v12, m_v21, m_v22;
};
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境:
VS2022 C++17

相关文章:

[二分查找]LeetCode2040:两个有序数组的第 K 小乘积
本文涉及的基础知识点 二分查找算法合集 题目 给你两个 从小到大排好序 且下标从 0 开始的整数数组 nums1 和 nums2 以及一个整数 k ,请你返回第 k (从 1 开始编号)小的 nums1[i] * nums2[j] 的乘积,其中 0 < i < nums1.…...

【Godot4.2】颜色完全使用手册
概述 本篇简单汇总Godot中的颜色的构造和使用,内容包括了: RGB、RGBA,HSV以及HTML16进制颜色值、颜色常量等形式构造颜色颜色的运算以及取反、插值用类型化数组、紧缩数组或PNG图片形式存储多个颜色 构造颜色 因为颜色是一种视觉元素&…...
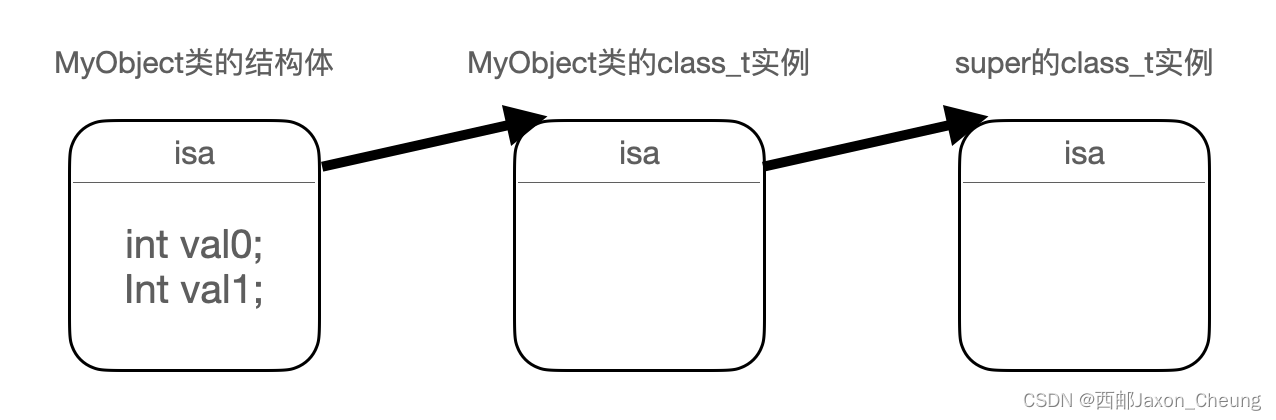
Blocks —— 《Objective-C高级编程 iOS与OS X多线程和内存管理》
目录 Blocks概要什么是BlocksOC转C方法关于几种变量的特点 Blocks模式Block语法Block类型 变量截获局部变量值__block说明符截获的局部变量 Blocks的实现Block的实质 Blocks概要 什么是Blocks Blocks是C语言的扩充功能,即带有局部变量的匿名函数。 顾名思义&#x…...

Python零基础---爬虫技术相关
python 爬虫技术,关于数据相关的拆解: 1.对页面结构的拆解 2.数据包的分析(是否加密了参数)(Md5 aes)难易程度,价格 3.对接客户(433,334) # 数据库 CSV 4.结单(发一部分数据&a…...
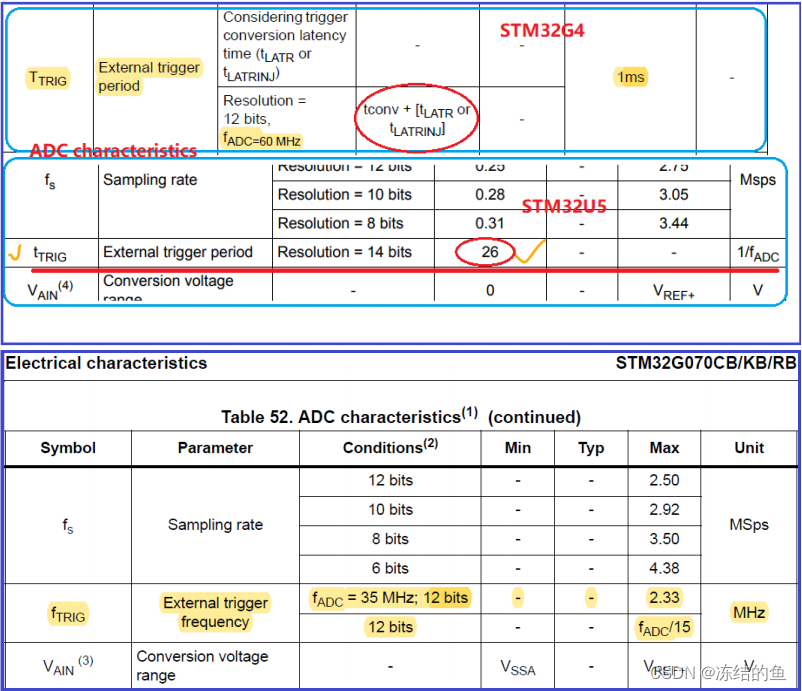
利用 STM32 TIMER 触发 ADC 实现分组转换
1、问题描述 使用 STM32G4 系列芯片开发产品,用到其中一个 ADC 模块的多个通道,他希望使 用 TIMER 来定时触发这几个通道的转换。不过他有两点疑惑。第一,他期望定时器触发这几个 通道是每触发一次则只转换一个通道,这样依次触发…...

2024 年(第 12 届)“泰迪杯”数据挖掘挑战赛——B 题:基于多模态特征融合的图像文本检索完整思路与源代码分享
一、问题背景 随着近年来智能终端设备和多媒体社交网络平台的飞速发展,多媒体数据呈现海量增长 的趋势,使当今主流的社交网络平台充斥着海量的文本、图像等多模态媒体数据,也使得人 们对不同模态数据之间互相检索的需求不断增加。有效的信…...

Java12~14 switch语法
JDK8以后的语法没学习了,现在时代发展这么快,所以得加紧时间学习了。JDK12只有一个特性就是switch语法,算是比较容易学习的一个版本吧。总体来说就是三部分内容。具体内容可以看JEP-325的内容。 箭头语法 每个case可以放箭头了。以下是一个例…...
小狐狸ChatGPT智能聊天系统源码v2.7.6全开源Vue前后端+后端PHP
测试环境包括Linux系统的CentOS 7.6,宝塔面板,PHP 7.4和MySQL 5.6。网站的根目录是public, 使用thinkPHP进行伪静态处理,并已开启SSL证书。 该系统具有多种功能,包括文章改写、广告营销文案创作、编程助手、办公达人…...
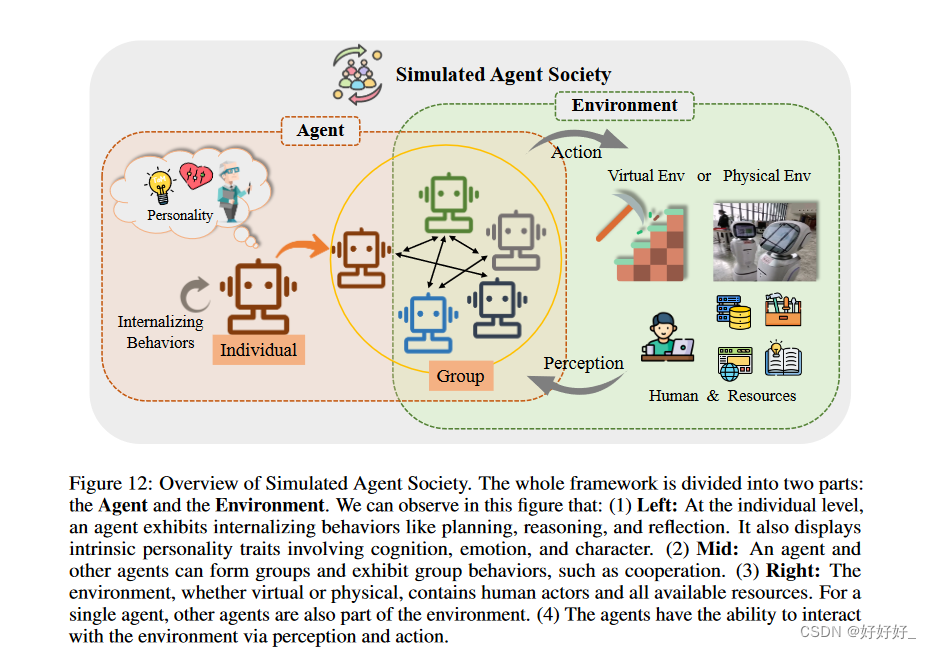
The Rise and Potential of Large Language Model Based Agents: A Survey
OpenAI AI的应用研究主管Lilian Weng发布了关于AI Agents的《大语言模型(LLM)支持的自主代理》,在文章中她定义了基于LLM构建AI Agents的应用框架:AgentLLM(大型语言模型)记忆(Memory࿰…...
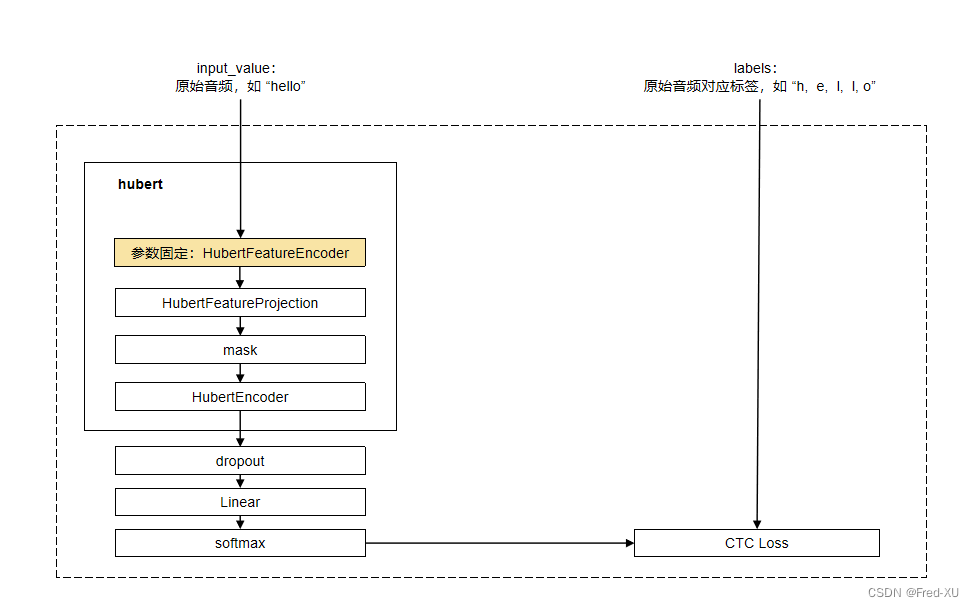
【GPT-SOVITS-06】特征工程-HuBert原理
说明:该系列文章从本人知乎账号迁入,主要原因是知乎图片附件过于模糊。 知乎专栏地址: 语音生成专栏 系列文章地址: 【GPT-SOVITS-01】源码梳理 【GPT-SOVITS-02】GPT模块解析 【GPT-SOVITS-03】SOVITS 模块-生成模型解析 【G…...
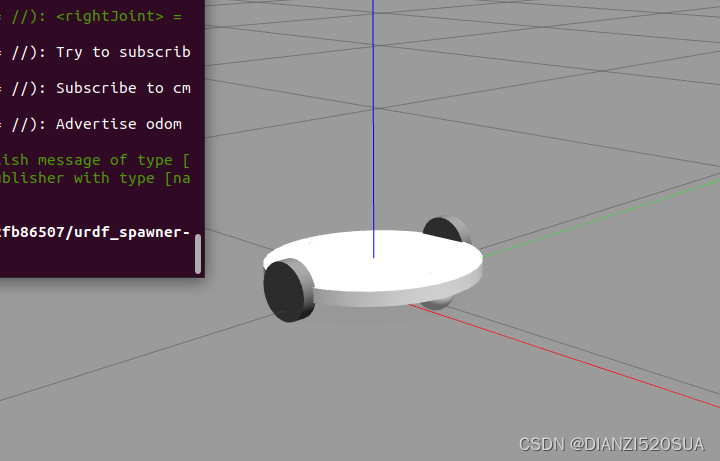
ros小问题之差速轮式机器人轮子不显示(rviz gazebo)
在rviz及gazebo练习差速轮式机器人时,很奇怪,只有个机器人的底板及底部的两个万向轮,如下图, 后来查看相关.xacro文件,里面是引用包含了轮子的xacro文件,只需传入不同的参数即可调用生成不同位置的轮子&…...
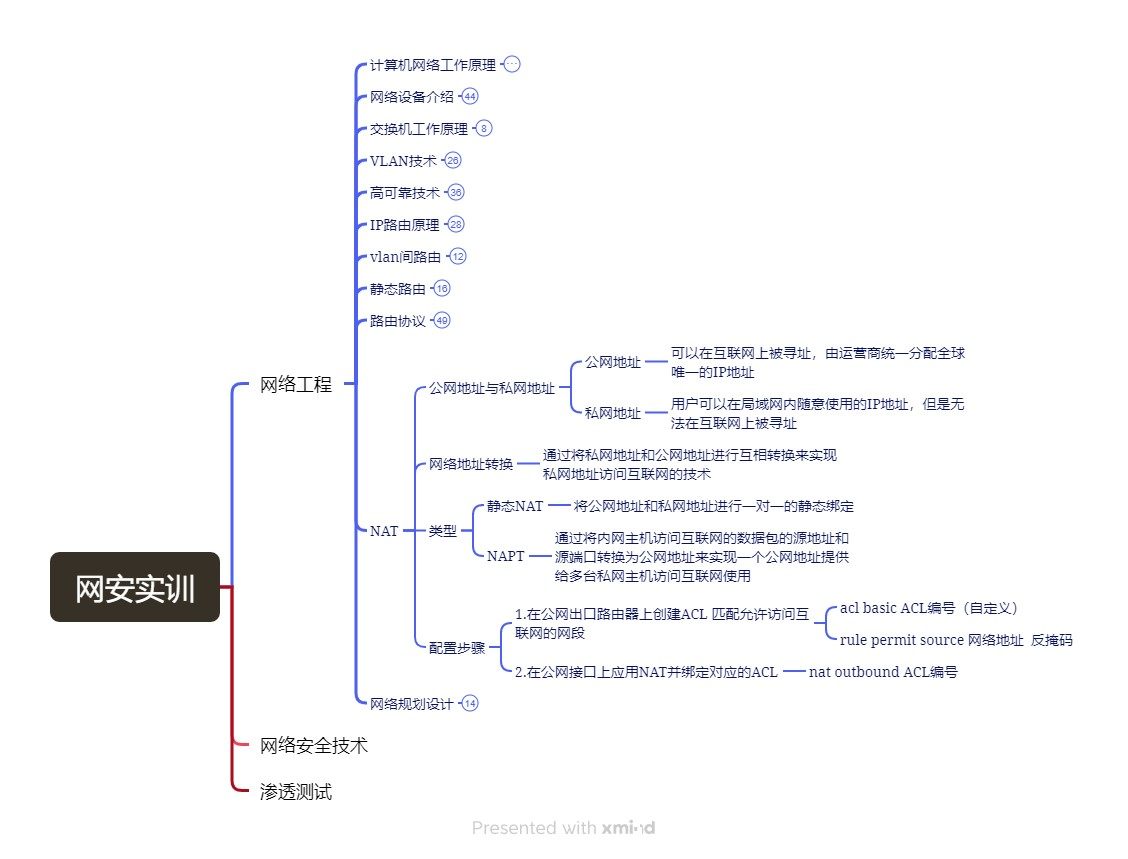
网络安全实训Day5
写在前面 昨天忘更新了......讲的内容不多,就一个NAT。 之前记的NAT的内容:blog.csdn.net/Yisitelz/article/details/131840119 网络安全实训-网络工程 NAT 公网地址与私网地址 公网地址 可以在互联网上被寻址,由运营商统一分配全球唯一的I…...

【Unity入门】详解Unity中的射线与射线检测
目录 前言一、射线的创建方法二、射线检测1、Raycast()Raycast()不使用射线RayRaycast()使用射线Ray 2、RaycastAll()使用射线RayRaycastAll() 不使用射线Ray 3、射线的碰撞信息 三、示例四、具体使用场景射线的调试方法1、Debug.DrawLine()2、Debug.DrawRay利用Gizmos 前言 碰…...
)
实验11-2-5 链表拼接(PTA)
题目: 本题要求实现一个合并两个有序链表的简单函数。链表结点定义如下: struct ListNode {int data;struct ListNode *next; }; 函数接口定义: struct ListNode *mergelists(struct ListNode *list1, struct ListNode *list2); 其中lis…...
Mybatis Plus + Spring 分包配置 ClickHouse 和 Mysql 双数据源
目录 一、背景 二、各个配置文件总览(文件位置因人而异) 2.1 DataSourceConfig 2.2 MybatisClickHouseConfig (ClickHouse 配置类) 2.3 MybatisMysqlConfig(Mysql 配置类) 2.4 application.propertie…...
)
27-3 文件上传漏洞 - 文件类型绕过(后端绕过)
环境准备:构建完善的安全渗透测试环境:推荐工具、资源和下载链接_渗透测试靶机下载-CSDN博客 导语 后端校验由开发决定是检测文件后缀,还是文件内容。 文件类型绕过(Content-Type) 1)MIME 类型 定义:MIME(Multipurpose Internet Mail Extensions)类型是一种标准,…...

widget一些控件的使用
QRadioButton使用 先使用ui界面拖拽创建radio button #include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);ui->male->setChecked(true);//选中按钮ui->o…...

Python基础(七)之数值类型集合
Python基础(七)之数值类型集合 1、简介 集合,英文set。 集合(set)是由一个或多个元素组成,是一个无序且不可重复的序列。 集合(set)只存储不可变的数据类型,如Number、…...

电脑充电器能充手机吗?如何给手机充电?
电脑充电器可以给手机充电吗? 电脑充电器可以给手机充电,但前提是电脑充电器的功率输出与手机的功率匹配且接口匹配。 假设电脑充电器的输出功率为5V/2A,手机也支持5V/2A的输入功率。 只要接口匹配,就可以使用电脑充电器给手机充…...

矩阵中移动的最大次数
文章目录 所属专栏:BFS算法 题目链接 思路如下: 1.首先我们需要从第一列开始遍历,寻找每一个都能够满足条件的位置,将它插入到数组里面 2.第一列遍历完了后我们先判断第一列的数是否都满足条件插入到数组里面,如果数组为空&#…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
