数据结构/C++:红黑树
数据结构/C++:红黑树
- 概念
- 实现
- 基本结构
- 插入
- uncle为红色节点
- uncle为黑色节点
- 总代码展示
概念
红黑树是一种二叉搜索树,一般的二叉搜索会发生不平衡现象,导致搜索效率下降,于是学者们开始探索如何让二叉搜索树保持平衡,这种树叫做自平衡二叉搜索树。起初学者发明了AVL树,其通过一定算法保持了二叉搜索树的严格平衡,不久后Rudolf Bayer发明了红黑树,红黑树的平衡是较为宽泛的,为了保持平衡,红黑树付出的代价比AVL树更小。因此红黑树被更为广泛的使用,比如Java,C++,python中,使用的自平衡二叉搜索树都是红黑树,而不是AVL树。
如果想了解AVL树,可以看这篇博客:[数据结构/C++:AVL树]
红黑树的要求如下:
红黑树中,最长路径的长度不会超过最短路径的两倍
先解释一下路径的概念:从根走到nullptr。
有不少人认为路径是从根走到叶子节点,这是不正确的。
红黑树用了五条规则来限制一棵树,从而达到以上要求:
- 每个节点不是红色就是黑色
- 根节点一定是黑色
- 不可以出现连续的红色节点(黑色可以连续出现)
- 每一条路径都包含相同数目的黑色节点
nullptr视为黑色节点
只要满足以上五个条件,那么这棵树就是一颗红黑树,而且满足最长路径的长度不会超过最短路径的两倍。为什么呢?
五条规则中,我标红了3,4两条规则:
- 不可以出现连续的红色节点(黑色可以连续出现)
- 每一条路径都包含相同数目的黑色节点
由于每一条路径都必须包含相同数目的黑色节点,现在我们假设一棵红黑树,所有路径的黑色节点数目都是x,那么最短的路径长度就是全为黑色节点,长度为x。
如果想让一条路径变长,那么就只能插入更多的红色节点(因为黑色节点数目相同),但是红色节点又不能连续出现,所以只能是黑红黑红黑红黑红黑红......这样排列,一个黑节点匹配一个红节点,因此最长路径的长度就是黑色节点的两倍2x。
可以发现,红黑树通过这两条核心规则,保证了二叉搜索树的平衡。
比如以下就是一颗红黑树:
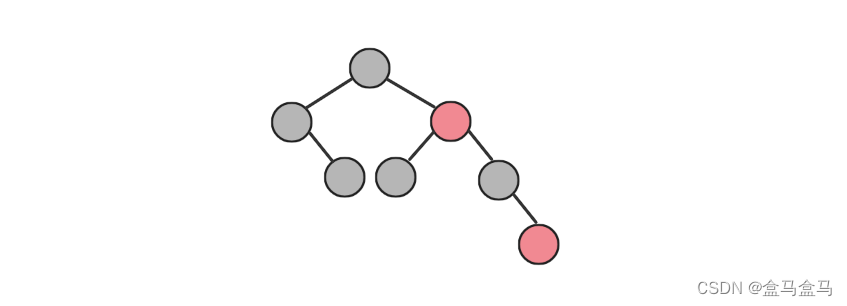
其最短路径为最左侧的路径,长度为2,即两个黑节点。
其最长路径为最右侧的路径,长度为4,即一红一黑排列。
要注意的是:不是所有的红黑树都会出现以上的全黑路径,或者一红一黑路径的,这只是极端情况。
接下来我们通过实现红黑树,来了解红黑树是如何自平衡的:
实现
基本结构
首先我们要在节点中加入一个成员来表示节点的颜色,颜色有红黑和黑色两种状态,这里我使用枚举来区分两者:
enum Colour
{RED,BLACK
};
在某些红黑树的实现中,使用bool值来表示红黑颜色,这也是可以的,但是本博客以枚举来表示颜色。
节点类:
template<class K, class V>
struct RBTreeNode
{RBTreeNode* _left;RBTreeNode* _right;RBTreeNode* _parent;pair<K, V> _kv;Colour _col;
};
_left:左子树
_right:右子树
_parent:父节点
_kv:节点存储的值
_col:该节点的颜色
节点类还需要一个构造函数进行初始化,现在的问题就是:新的节点要初始化为什么颜色?
先来考虑一下:插入红色节点和插入黑色节点,谁对红黑树影响大?
对于一棵红黑树,其所有路径的黑色节点数目都相同,如果我们在某一条路径末尾插入了黑色节点,那么整棵树的所有其它路径都会少一个黑节点。而插入红色节点只影响当前路径,所以新节点应该是红色节点。
构造函数:
RBTreeNode(const pair<K, V>& kv): _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED)//初始化为红节点
{}
接着就是红黑树本体,类中只存储一个根节点_root:
template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
private:Node* _root = nullptr;
}
现在我们有了红黑树的基本结构,接下来就实现它的插入操作:
插入
那么我们先写出当基本的二叉搜索树的插入代码逻辑,既然要插入,那么就要先找到合适的位置插入,代码如下:
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//保持根为黑节点}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first > kv.first)parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;//调整红黑树//......//......//......return true;
}
接下来,我先解析以上代码的逻辑:
if (_root == nullptr) {_root = new Node(kv);_root->_col = BLACK;//保持根为黑节点 }如果我们插入节点时,根节点
_root为空,说明当前整棵树都为空,那么我们直接插入值作为根节点即可,但是根节点必须是黑色节点,而我们新插入的节点是红色,所以要将其调整为黑色节点。
while (cur) {if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;} }以上代码,是在找到合适的插入位置,当
key大于当前节点cur->_kv.first < kv.first,那么cur就向左寻找,反之向右寻找。如果当前节点值等于key,那么说明该节点已经存在,返回false代表插入失败。当我们的cur为空指针,说明已经找到了插入的节点,此时跳出循环进行插入。
cur = new Node(kv);if (parent->_kv.first > kv.first)parent->_left = cur; elseparent->_right = cur;cur->_parent = parent;到达此处,说明前面已经找到插入的位置了,而
parent节点就是插入位置的父亲节点。根据key的大小,来判断插入到左边还是右边,插入完成后,再让新节点的_parent指向parent。
至此我们就完成了插入操作,接下来就要根据不同情况对红黑树进行调整。
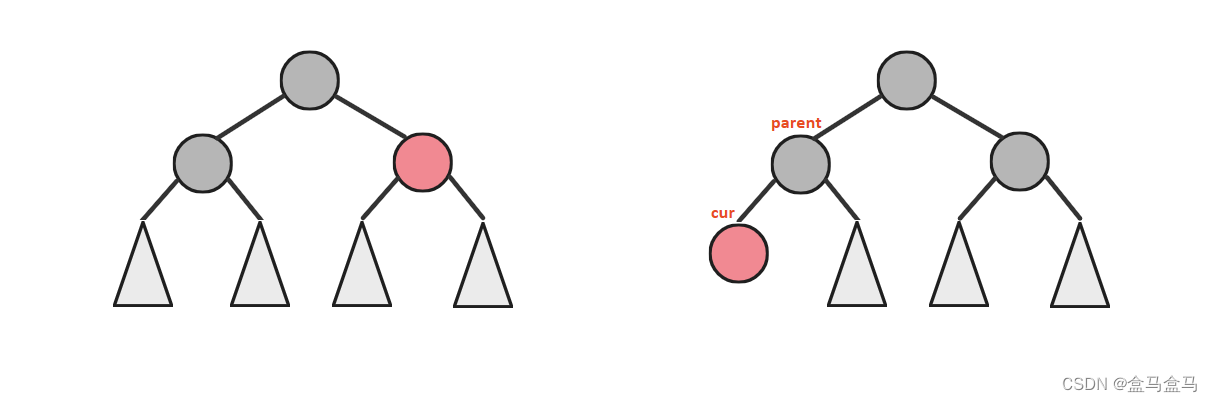
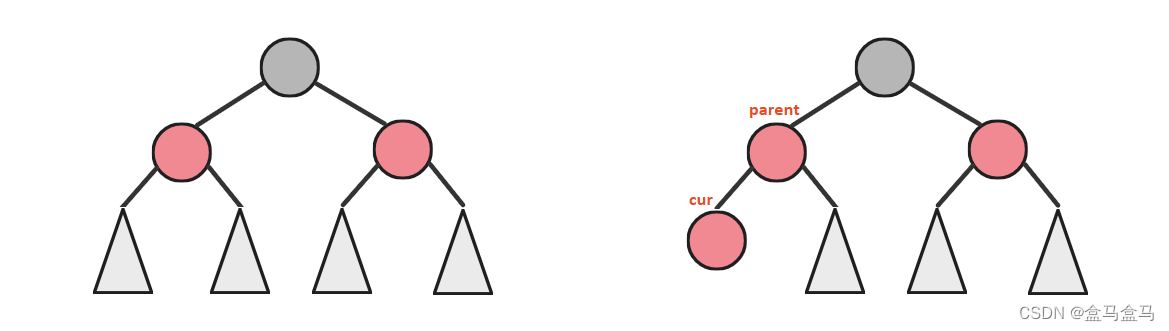
对于红黑树的插入,我们需要关注新节点的父亲parent,祖父grandfather,叔叔uncle三个节点:
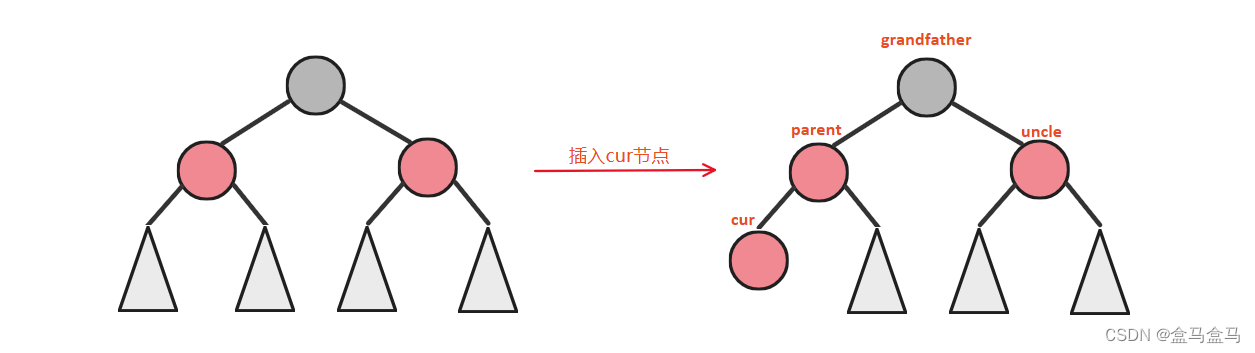
- 先根据父亲节点的颜色,来判断是否需要调整
父亲节点为黑色:
新插入的节点默认为红色,所以新插入节点不会影响路径上黑色节点的数目,而parent是黑节点,我们也没有出现连续的红色节点,所以这种情况无需任何调整,直接插入就可以。
父亲节点为红色:
如果父亲节点为红色,我们就会出现连续的红色节点,这时我们就需要进行调整了
以上两种情况总结为:
当
parent为黑色,直接插入
当parent为红色,插入后需要进行调整
当parent为红色,我们就需要再根据uncle的颜色,将插入分类两类:uncle为红色以及uncle为黑色。
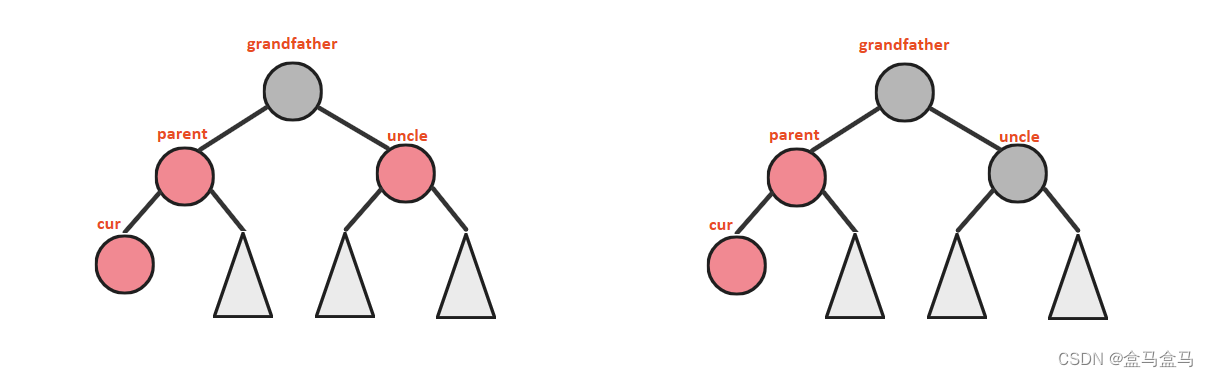
值得注意的是:由于parent是红色节点,此时的grandfather一定是黑色节点,因为不能出现连续红色节点
这两种情况的操作不同,我们先看到uncle为红色的情况:
uncle为红色节点
当
uncle节点为红色,此时需要进行变色
变色如下:
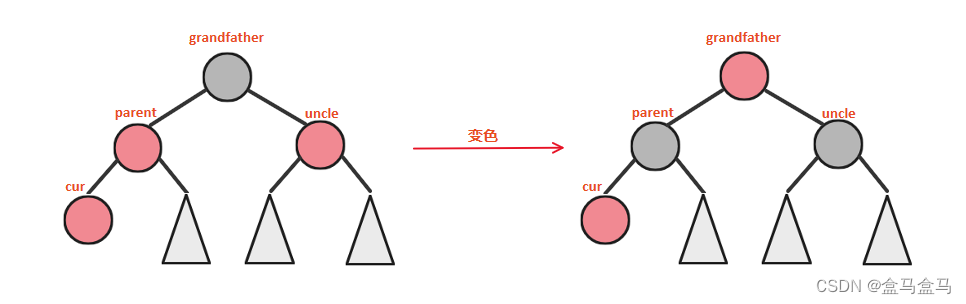
由于新插入了红色的cur节点,此时parent与cur出现了连续的红色节点,于是我们将parent改为黑色。但是此时以parent为根的所有路径就会多出一个黑节点,于是把grandfather变为红色,来抵消这个新增的黑节点。但是此时以uncle为根的路径又会少一个黑节点,于是把uncle变黑。
但是我们将grandfather变为了红色,这有可能会影响到上一层节点,比如这样:
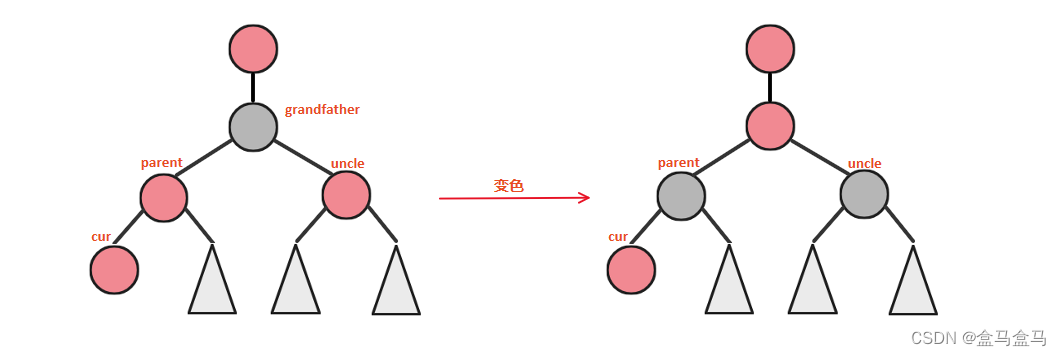
我们把grandfather变红之后,又出现了两个红色节点相连的情况,所以我们要写一个while循环,来反复向上检查。
当前代码如下:
while (parent && parent->_col == RED)//只有parent为红,才更新 (parent可能不存在)
{Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//uncle存在且为红节点if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//uncle为黑节点 {//其它处理}}else{Node* uncle = grandfather->_left;//uncle存在且为红节点if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//uncle为黑节点 {//其它处理}}
}_root->_col = BLACK;//在循环内部不判断root情况,统一处理
代码解析:
while (parent && parent->_col == RED)该代码用于检测
cur的parent的颜色,通过我们前面的推导,如果parent为红色才需要调整,因此进入循环的条件之一是parent为红色。另外的parent有可能为nullptr,此时我们要避免访问空指针,所以空指针也不能进循环
if (parent == grandfather->_left) { } else { }这一段代码是在检测
parent节点是grandfather的左子树还是右子树,这将涉及到我们如何找uncle以及下一种情况的调整,此时我们要分类讨论。当parent == grandfather->_left成立,那么uncle就是grandfather的右子树:Node* uncle = grandfather->_right;,反之就是左子树
if (uncle && uncle->_col == RED) {parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent; }我们找到
uncle后,如果uncle是红色,那么直接进行变色操作,把parent和uncle的颜色变为黑色,grandfather变为红色。
随后由于我们的变色操作可能会影响上一层,此时调整节点,进入下一次while循环
在整个
while循环外侧,还有一句代码:_root->_col = BLACK;这是因为我们在先前的while循环中,有可能出现对
_root节点的操作,导致_root的颜色改变,而_root需要保持黑色。如果我们在循环内部,每一次都检测_root有点麻烦了,于是我们直接在每一次调整完节点后,把_root强行矫正为黑色
至此我们就讨论完了uncle为红色节点的情况,接下来我们就讨论uncle为黑色节点:
uncle为黑色节点
由于红黑树中,nullptr也算作黑色节点,所以uncle为黑色分为以下两种情况:
uncle为空指针uncle不为空指针
图示如下:
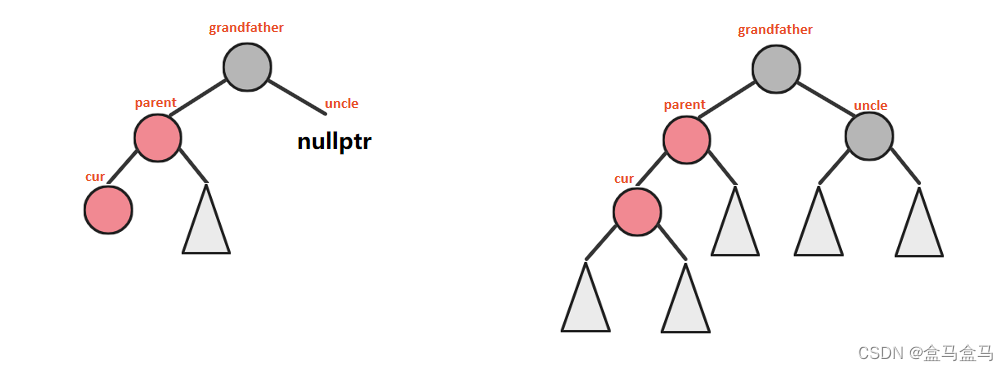
如果
uncle为空指针,那么cur一定是新插入的节点。
因为如果cur不是新插入的节点,那么cur和parent一定有一个原先是黑色节点,不然会出现连续的红色节点。但是如果cur和parent有一个是黑色节点,那么grandfather的左子树就比右子树多出一个黑节点,这就违背了红黑树规则。无论怎样,原先的树都不可能符合规则,所以cur一定是新插入的节点,破坏了规则。
如果
uncle不为空指针,那么cur一定是从黑色节点变成的红色节点(不是新插入的)。
因为如果uncle存在,那么grandfather的右子树就存在一个黑节点,而parent是红节点,所以cur和parent的右子树中都至少有一个黑节点,才能保证每一条路径黑节点数目相同。因此cur原先一定是黑节点,是因为cur下层插入了新节点,然后通过while循环向上走,影响到了当前层。
对于这种uncle为黑色的情况,我们需要通过旋转+变色来维持红黑树。
旋转又分为单旋和双旋:
当
cur与parent的关系和parent与grandfather的关系一致时,需要进行单旋
比如我们刚刚的情况:

cur是parent的左子树,parent是grandfather的左子树,关系一致。
我们需要对其进行右单旋+变色:
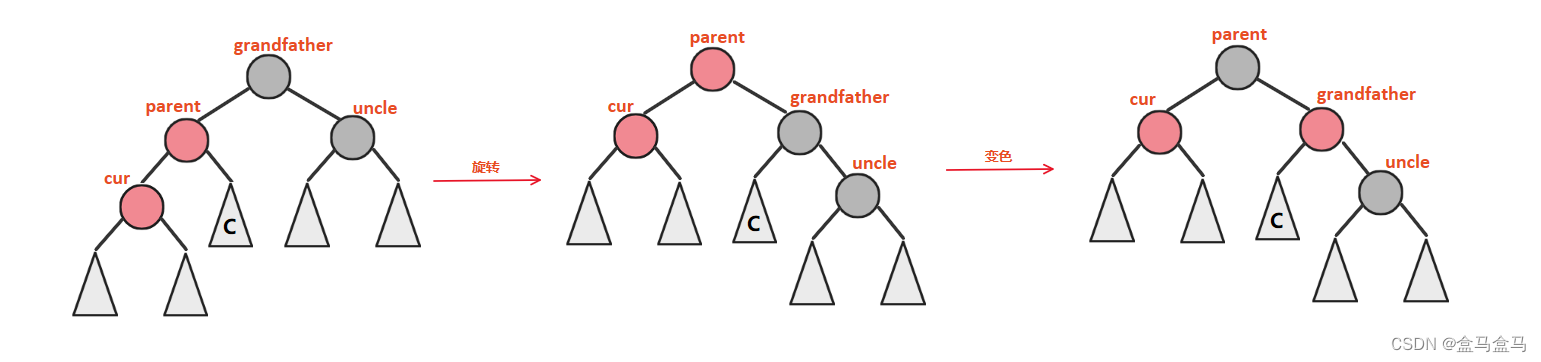
这个旋转的算法在此我就不过多讲解了,可以去AVL树的博客中了解。我重点讲解一下变色和旋转的合理性:
一次插入过程中,走到这一步,说明前面一定经过了
uncle为红色的情况,而对uncle为红色的情况进行变色并不会对任何路径的黑色节点数目造成影响,因此目前还是符合黑色节点数目相同规则的。
同为parent的子树,以cur和C为根的路径,黑节点数目相同
同为grandfather的子树,以parent和uncle为根的路径黑节点数目相同
而parent是红色节点,所以cur,C以及uncle为根的路径,黑节点数目都相同
进行单旋,会把
c树交给grandfather做子树,而c与uncle为根的路径黑节点数目相同,不违背规则(旋转的合理性)
旋转后,
parent作新根,grandfather与cur作为左右子树grandfather为根的路径,整体上就会比以cur为根的路径多出一个黑节点(即grandfather本身)
因此,将grandfather改为红节点,来平衡parent左右子树的黑节点
而红色节点不能连续出现,再把parent改为黑节点
当
cur与parent的关系和parent与grandfather的关系不一致时,需要进行双旋
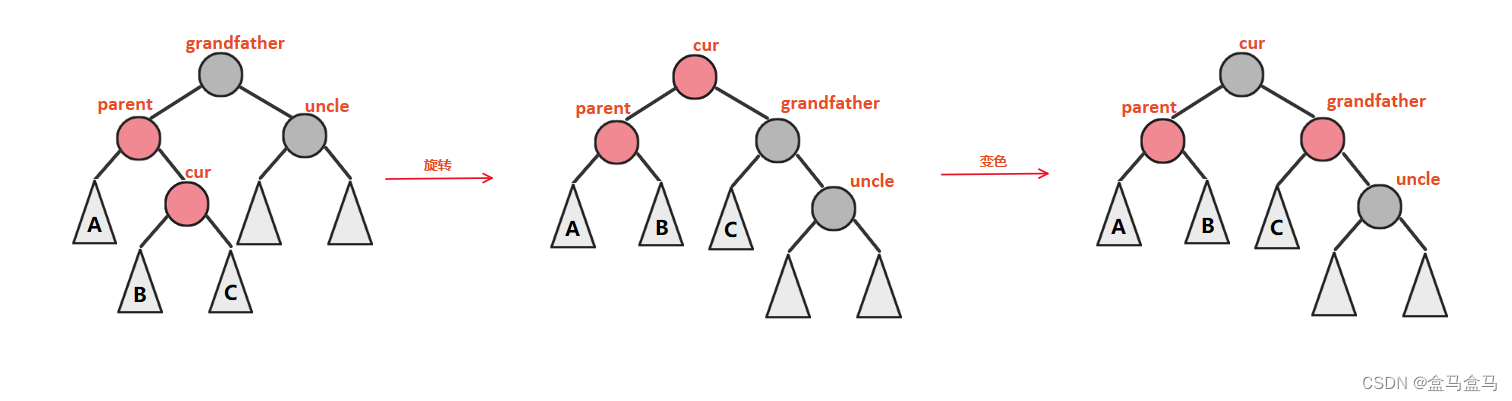
以上结构中,cur是parent的左子树,parent是grandfather的右子树,关系不一致,要进行双旋。
同样的,讲解一下变色和旋转的合理性:
一次插入过程中,走到这一步,说明前面一定经过了
uncle为红色的情况,而对uncle为红色的情况进行变色并不会对任何路径的黑色节点数目造成影响,因此目前还是符合黑色节点数目相同规则的。
同为parent的子树,以cur和A为根的路径,黑节点数目相同
同为cur的子树,以B和C为根的路径,黑节点数目相同
由于cur是红节点,所以以A,B,C为根的路径,黑节点数目相同
相同的手段,由于parent是红节点,所以A与uncle为根的路径的黑节点数目相同
因此A,B,C,uncle为根的路径,黑节点数目都相同
进行双旋,会把
C子树交给grandfather做子树,而C与uncle黑节点数目相同,不违背规则也会把B交给parent做子树
A与B黑节点数目相同,不违背规则
旋转后,cur作新根,grandfather与parent作为左右子树grandfather为根的路径,整体上就会比以parent为根的路径多出一个黑节点(grandfather本身)
因此,将grandfather改为红节点,来平衡cur左右子树的黑节点而红色节点不能连续出现,再把cur改为黑节点
以上单旋和双旋的变色,看似复杂,其实最后都是把新根的颜色变为黑色,新根的左右子树变为红色。由于我们旋转后,新根都是黑节点,所以不会影响上层,可以直接跳出循环。
代码如下:
当parent == grandfather->_left:
else//uncle为黑节点 (旋转)
{if (cur == parent->_left){RotateR(grandfather);//右单旋parent->_col = BLACK;//变色grandfather->_col = RED;//变色}else{RotateL(parent);//左右双旋 - 左单旋RotateR(grandfather);//左右双旋 - 右单旋cur->_col = BLACK;//变色grandfather->_col = RED;//变色}break;//旋转后一定平衡
}
当parent == grandfather->_right:
else//uncle为黑节点 (旋转)
{if (cur == parent->_right){RotateL(grandfather);//左单旋parent->_col = BLACK;//变色grandfather->_col = RED;//变色}else{RotateR(parent);//右左双旋 - 右单旋RotateL(grandfather);//右左双旋 - 左单旋cur->_col = BLACK;//变色grandfather->_col = RED;//变色}break;//旋转后一定平衡
}
insert总代码:
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//保持根为黑节点}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first > kv.first)parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;while (parent && parent->_col == RED)//只有parent为红,才更新 (parent可能不存在){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//uncle存在且为红节点if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//uncle不存在或为黑节点 (旋转){if (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//旋转后一定平衡}}else{Node* uncle = grandfather->_left;//uncle存在且为红节点if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//uncle不存在或为黑节点 (旋转){if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//旋转后一定平衡}}}_root->_col = BLACK;//在循环内部不判断root情况,统一处理return true;
}
总代码展示
红黑树总代码:
RBTree.h:
#pragma once
#include <iostream>
#include <assert.h>
using namespace std;enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode* _left;RBTreeNode* _right;RBTreeNode* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv): _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//保持根为黑节点}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first > kv.first)parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;while (parent && parent->_col == RED)//只有parent为红,才更新 (parent可能不存在){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//uncle存在且为红节点if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//uncle不存在或为黑节点 (旋转){if (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//旋转后一定平衡}}else{Node* uncle = grandfather->_left;//uncle存在且为红节点if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//uncle不存在或为黑节点 (旋转){if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;//旋转后一定平衡}}}_root->_col = BLACK;//在循环内部不判断root情况,统一处理return true;}//左单旋void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppNode = parent->_parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (ppNode->_left == parent)ppNode->_left = subR;elseppNode->_right = subR;subR->_parent = ppNode;}}//右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppNode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent)ppNode->_left = subL;elseppNode->_right = subL;subL->_parent = ppNode;}}size_t Size(){return _Size(_root);}size_t _Size(Node* root){if (root == nullptr)return 0;;return _Size(root->_left) + _Size(root->_right) + 1;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;}//中序void InOrder(){_InOrder(_root);cout << "end" << endl;}int Height(){return _Height(_root);}private://中序void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " - ";_InOrder(root->_right);}//求高度int _Height(Node* root){if (root == nullptr)return 0;return max(Height(root->_left), Height(root->_right)) + 1;}Node* _root = nullptr;
};
相关文章:

数据结构/C++:红黑树
数据结构/C:红黑树 概念实现基本结构插入uncle为红色节点uncle为黑色节点 总代码展示 概念 红黑树是一种二叉搜索树,一般的二叉搜索会发生不平衡现象,导致搜索效率下降,于是学者们开始探索如何让二叉搜索树保持平衡,这…...
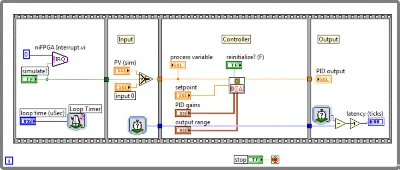
【LabVIEW FPGA入门】浮点数类型支持
如今,使用浮点运算来设计嵌入式系统的需求变得越来越普遍。随着 FPGA 因其固有的大规模并行性而在浮点性能方面继续超越微处理器,这种情况正在加剧。线性代数和数字信号处理 (DSP) 等高级算法可以受益于浮点数据类型的高动态范围精度。LabVIEW FPGA 通过…...
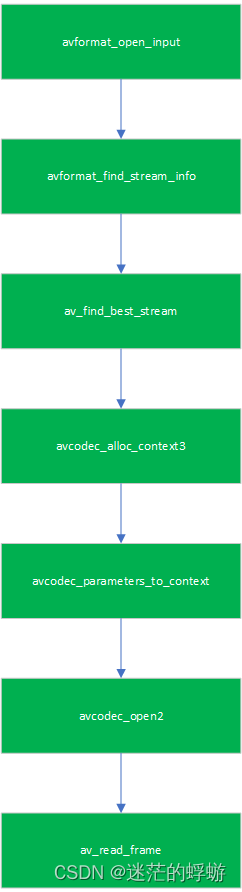
ffmpeg 滤镜实现不同采样率多音频混音
音频混音在音视频开发中是十分重要的一个环节,所谓音频混音就是将所有需要混音的数据相加得到混音数据,然后通过某个算法进行非法数据的处理;例如相加数值超过最大值,最小值等! 在实际的音频开发中,要实现混音的流程如下: 因此我们的编码实现就分为五部分:寻找…...

UserTCP 传输数据时如何保证数据的可靠性?并以LabVIEW为例进行说明
TCP(传输控制协议)是一种面向连接的、可靠的、基于字节流的传输层通信协议。它通过多种机制保证数据的可靠性,确保数据在网络中从一端传输到另一端时,顺序正确且无误差。以下是TCP实现数据可靠性的一些关键机制: 1. 三…...
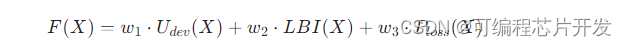
基于粒子群算法的分布式电源配电网重构优化matlab仿真
目录 1.课题概述 2.系统仿真结果 3.核心程序与模型 4.系统原理简介 4.1基本PSO算法原理 4.2配电网重构的目标函数 5.完整工程文件 1.课题概述 基于粒子群算法的分布式电源配电网重构优化。通过Matlab仿真,对比优化前后 1.节点的电压值 2.线路的损耗,这里计…...
)
mysql提权总结(自学)
目录 MySQL数据库提权简介 UDF提权 原理 利用条件 利用准备 利用过程 MOF提权 原理 利用条件 利用过程 自启动提权 反弹shell提权 总结 MySQL数据库提权简介 一般数据库提权思路: 检测数据库的存在(探测端口)获取到数据库的权限…...

[数据集][目标检测]铝片表面工业缺陷检测数据集VOC+YOLO格式400张4类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):400 标注数量(xml文件个数):400 标注数量(txt文件个数):400 标注类别…...

晶体管-二极管三极管MOS管选型参数总结
🏡《总目录》 目录 1,概述2,二极管选型参数2.1,类型(Type)2.2,最大整流电流(IF)2.3,反向击穿电压(VRRM)2.4,正向压降(VF)2.5,反向电流(IR)2.6,结温(Tj)2.7,热阻(Rth)2.8,频率特性2.9,包装类型...

ssh命令——安全远程连接Linux服务器
ssh命令是Secure Shell的简写,其功能是安全地远程连接服务器,ssh是OpenSSH套件中的客户端连接工具,通过SSH加密协议进行远程主机访问,并对远程服务器进行管理。 ssh命令的基本语法格式如下: ssh [选项] 主机名或IP地…...

Ansible非标记语言YAML与任务剧本Playbook
前言 上篇介绍了 Ansible 单模块(AD-Hoc)的相关内容Ansible自动化运维Inventory与Ad-Hoc-CSDN博客,Ad-Hoc 命令是一次性的、即时执行的命令,用于在远程主机上执行特定任务,这些命令通常用于快速执行简单的任务。当需要…...
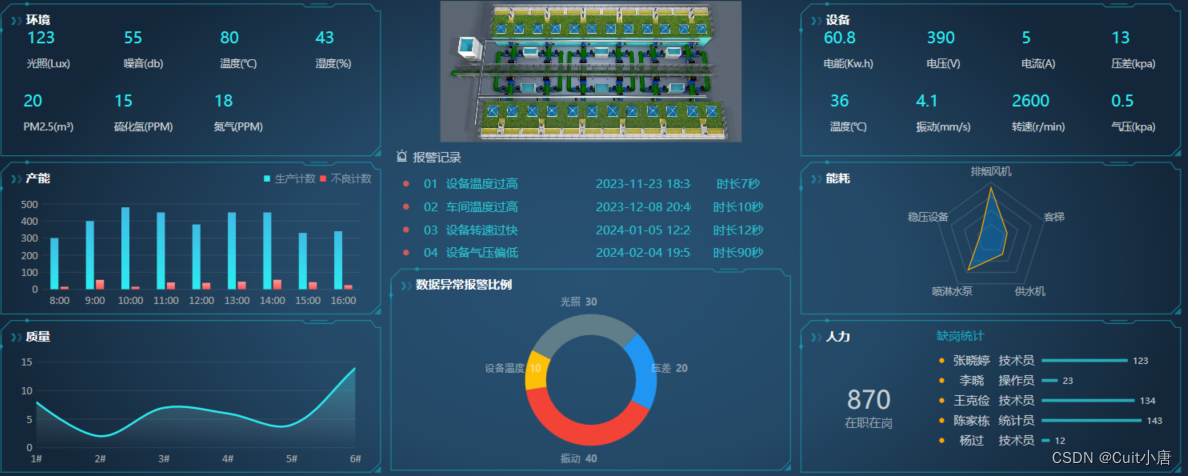
WPF监控平台(科技大屏)[一]
跟着B站的视频敲了一个略微复杂的WPF界面,链接如下.在这里我详细的写一份博客进行设计总结. 系统介绍和配置及主窗口设计_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1Wy421Y7QD?p1&vd_source4796b18a2e4c1ec8a310391a5644b6da 成果展示 实现过程 总体来说,我的…...

HTML详细教程
文章目录 前言一、快速开发网站最简模板二、HTML标签1.编码2.title3.标题4.div和span5.超链接6.图片7.列表8.表格9.input系列10.下拉框11.多行文本 三、GET方式和POST方式1.GET请求2.POST请求 前言 HTML的全称为超文本标记语言,是一种标记语言,是网站开发…...
)
【excel】常用的50个函数与基础操作(统计函数)
统计函数 (1)数组函数操作 1.【SUM】求和 SUM(数字1,数字2,数字3…) 2.【SUMIF】单条件求和 SUMIF (条件区域,条件,求和区域) 3.【SUMIFS】(单)多条件求和…...

MATLAB中的cell数组和结构体
MATLAB中的Cell数组和结构体 MATLAB作为一种高级编程语言和数值计算环境,为用户提供了多种数据结构,以便更灵活、高效地处理数据。其中,cell数组和结构体是两种非常重要的数据结构,它们在MATLAB编程和数据管理中发挥着关键作用。…...

Python深度学习之路:TensorFlow与PyTorch对比【第140篇—Python实现】
👽发现宝藏 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【点击进入巨牛的人工智能学习网站】。 Python深度学习之路:TensorFlow与PyTorch对比 在深度学习领域,Tens…...
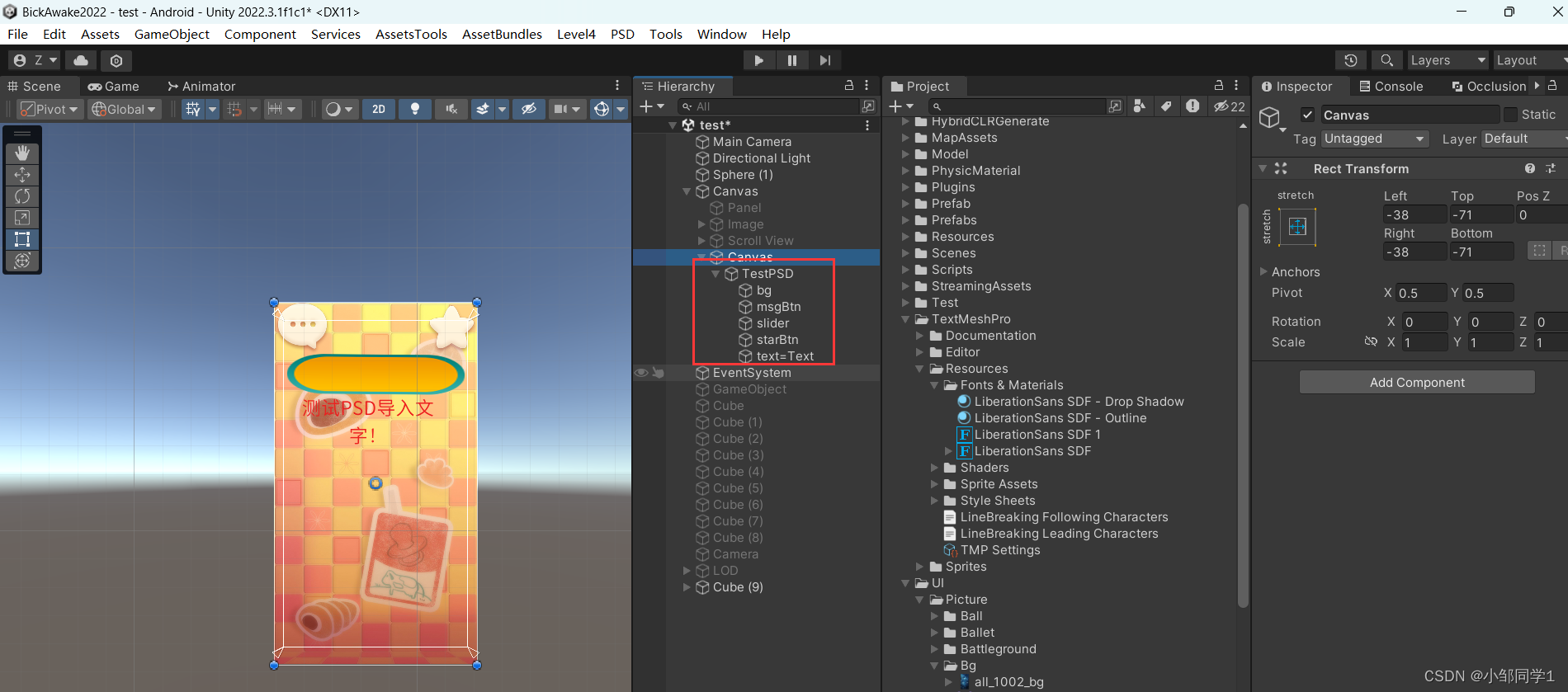
Unity中UGUI中的PSD导入工具的原理和作用
先说一下PSD导入工具的作用,比如在和美术同事合作开发一个背包UI业务系统时,美术做好效果图后,程序在UGUI中制作好界面,美术说这个图差了2像素,那个图位置不对差了1像素,另外一个图大小不对等等一系列零碎的…...

删除 Oracle 软件和数据库教程
1.使用 deinstall 工具删除安装的 Oracle 软件的可执行文件和配置文件 [oracleocpstudy admin]$ cd $ORACLE_HOME [oracleocpstudy db_1]$ cd deinstall [oracleocpstudy deinstall]$ ls bootstrap_files.lst bootstrap.pl deinstall deinstall.pl deinstall.xml jlib …...

C语言自学笔记8----C语言Switch语句
C 语言 switch 语句 switch语句使我们可以执行许多代替方案中的一个代码块。 虽然您可以使用if…else…if阶梯执行相同的操作。但是,switch语句的语法更容易读写。 switch … case的语法 switch (expression) { case constant1: // 语句 break; case constant2: // …...
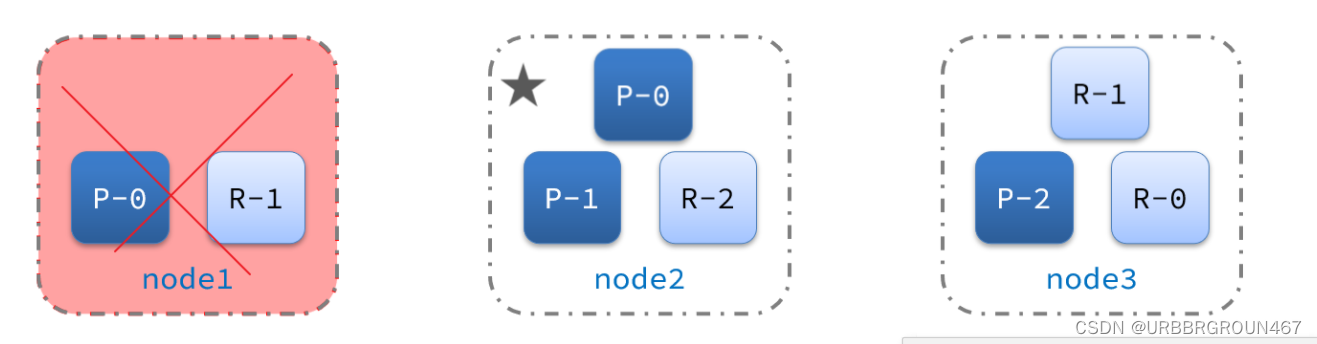
分布式搜索引擎(3)
1.数据聚合 **[聚合(](https://www.elastic.co/guide/en/elasticsearch/reference/current/search-aggregations.html)[aggregations](https://www.elastic.co/guide/en/elasticsearch/reference/current/search-aggregations.html)[)](https://www.ela…...
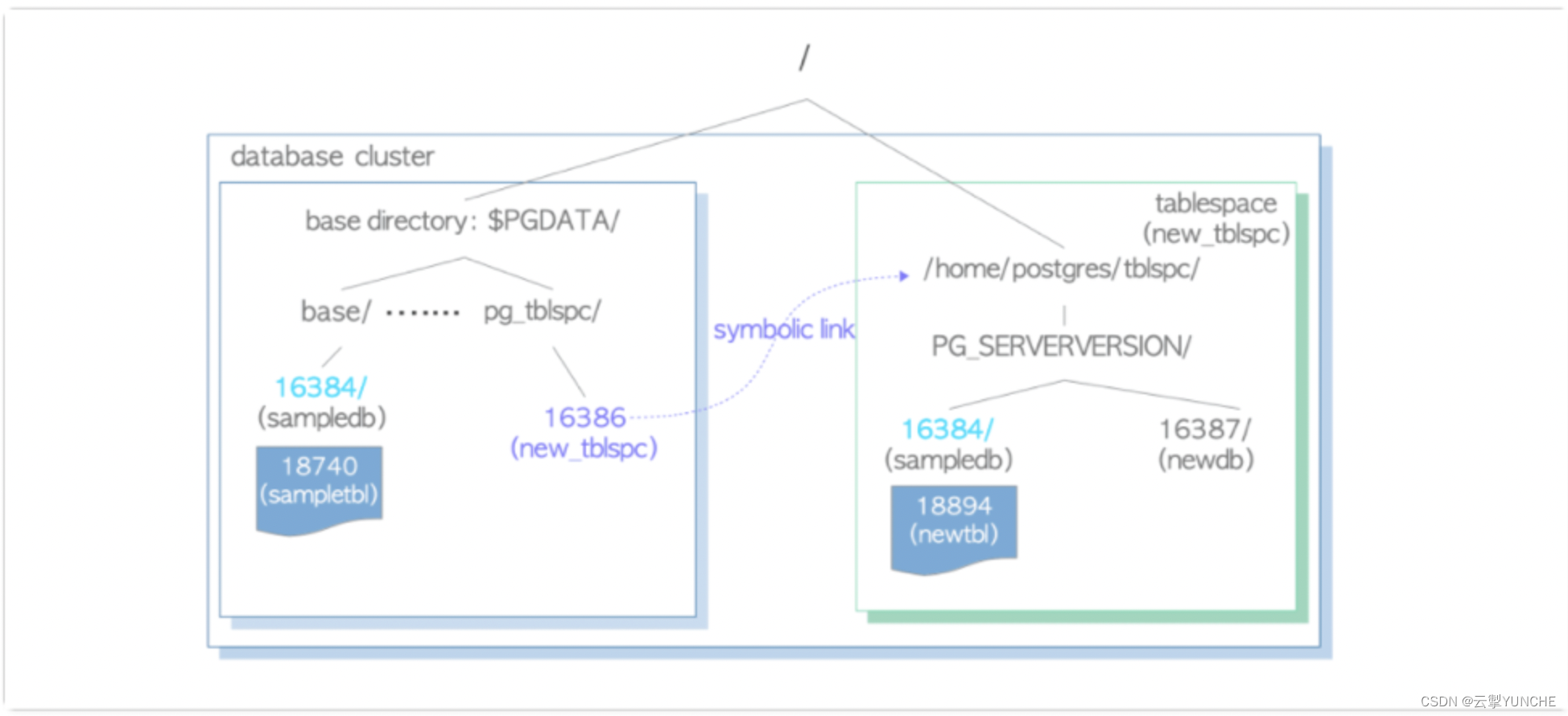
PostgreSQL开发与实战(6.3)体系结构3
作者:太阳 四、物理结构 4.1 软件安装目录 bin //二进制可执行文件 include //头文件目录 lib //动态库文件 share //文档以及配置模版文件4.2 数据目录 4.2.1 参数文件 pg_hba.conf //认证配置文件 p…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...